利用光变曲线估计猎鹰九号火箭末级的旋转状态研究*
苏向泽,汤儒峰,李荣旺,3,李语强,3
(1. 中国科学院云南天文台,云南 昆明 650216;2. 中国科学院大学,北京 100049;3.中国科学院空间目标与碎片观测重点实验室,江苏 南京 210034)
随着人类航天活动的开展,地球轨道上积攒了越来越多的空间碎片,这些空间碎片的存在对在轨运行的航天器以及载人航天活动带来很大的威胁[1]。火箭末级是指将目标航天器推入运行轨道的最后一级火箭,在完成任务后会绕地球按一定的轨道飞行,也属于空间碎片。火箭体尺寸大、重量大且运行姿态不受控制,严重影响附近正常工作的航天器,一旦相撞会发生连锁效应,产生更多的空间碎片。因为火箭体的姿态和轨道不受控制,为了了解这些大型空间碎片的运行状态,需要对其进行观测,获取相关信息。地基光度观测是最常用的观测手段,可以获取目标的光度信息[2]。由于目标的光度信息与运动、姿态、形状等多种因素相关,使用空间态势感知的不同方法可以分别将这些信息分离,从而得到目标的相关信息[3]。
国内外分析空间目标光度数据的方法主要有基于相位角的分析方法、基于极值点的分析方法[4]、基于光变曲线周期的分析方法[5]以及基于模型构建的分析方法等[6]。前3种方法主要根据观测得到的光变曲线,针对不同种类的空间目标分析方法也不同。但是这3种方法的适用目标有局限性,且只能针对某一特征进行分析。基于模型构建的分析方法主要包括基于非线性滤波的方法[7-8]、基于封闭面元模型分析方法和基于机器学习方法等,其中,基于非线性滤波的方法是分析空间目标特性的主要研究方法,通过构建目标运动和观测模型来预测其运动和姿态,需要精确的先验参数才能得到收敛的结果,不适用于先验参数较少的目标。本文主要根据观测到的火箭体光度数据,对处理后的光变曲线进行周期分析,确定火箭体的旋转周期,通过目标相位角和形状参数建立光度模型,对比观测光变曲线和理论计算得到的光变曲线估计旋转轴的指向。本文根据得到的收敛区间证明了构建光度模型方法的可行性,为研究其他类型的空间目标姿态提供参考。
1 猎鹰九号火箭末级信息
本文选择猎鹰九号火箭末级(编号:42 968)作为研究目标。猎鹰九号火箭是SpaceX公司研制的重型运载火箭,是现役运载能力最大的火箭之一,末级火箭的尺寸较其他火箭体更大,更易进行预报和光度观测,同时大尺寸也使得它对正常工作的航天器影响更大。了解其姿态可以更好地预测它的运动,从而使其他正常工作的航天器更好地规避碰撞风险。根据SpaceX公司发布的数据,42 968号目标是猎鹰九号中V1.2型火箭的火箭末级,如图1,去除下底面引擎后长约9.44 m,底面直径3.66 m,轨道为大椭圆形,近地点230 km,远地点33 819 km,具体信息如表1。

表1 目标42 968相关信息Table 1 Informations of target 42 968
2 光度数据的获取流程
本文采用地基光度测量的方法获取目标的光度信息,利用云南天文台1.2 m望远镜对目标进行观测。将采集的图像进行本底和平场改正、流量定标、斜距归一化等处理,得到目标的视星等及星等随时间变化的光变曲线。
2.1 图像采集
观测前从space-track网站(https://www.space-track.org)获取卫星的轨道数据,一般为双行根数格式(TLE)。双行根数的预报精度不高,应用到激光测距中需要修正[9],而本文观测使用的望远镜视场较大,可以不进行轨道修正。本文使用云南天文台1.2 m望远镜及30 cm导星镜、配套控制系统、CCD相机对目标进行观测并采集平场、定标星及目标的光度信息,使用SourceExtractor[10]软件提取定标星和待测目标的流量值。
观测时间为2019年12月13日和2019年12月15日,每次观测约30 min,具体信息如表2。图2是1.2 m望远镜拍摄的目标光度图像,中间的亮点为观测目标。图3为13日和15日观测时段内目标相对于望远镜方位角和高度角随时间变化的曲线,以极坐标的形式表示,13日用实线表示,15日用虚线表示,每段曲线的初始方位和高度角通过曲线中标注的点表示,可以看出在观测时段内目标的方位和高度变化不大。

表2 观测信息Table 2 The information of observation

图2 目标光度图像Fig.2 Object′s luminosity figure
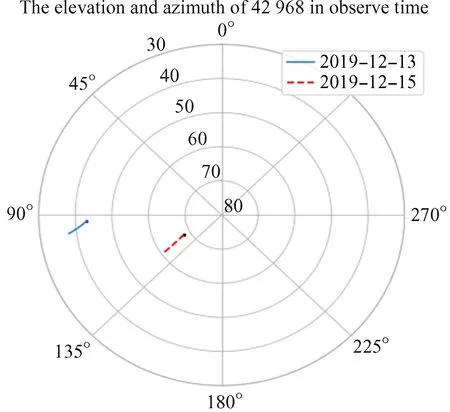
图3 观测时段内目标方位角与高度角Fig.3 Space object′s azimuth and elevation in observe periods
2.2 平场、本底处理及流量定标
我们首先对采集的本底与平场图像进行归一化处理,并计算经过平场处理后的图像灰度值:
(1)
其中,GO为原始图像的灰度值;Gbias为本底灰度值;Gflat为标准平场灰度值。根据现有的星表选择定标星并跟踪观测,由于望远镜视场较小,不能用场星定标,因此本文选择Landolt星表里的恒星G162,采集到光度图像后经过本底、平场归一化得到处理后的图像,这样可以消除望远镜光学系统对目标光度的影响。将处理后的图像与星表中的位置进行比对确定恒星,得到恒星光度流量值,再除以曝光时间,得到定标星单位时间内的流量值fcal,视星等值已知为Mcal=13.012,这样可以获得仪器的星等零点
M0=2.5log10fcal+Mcal,
(2)
从而计算得到目标的视星等
Mobj=-2.5log10fobj+M0,
(3)
其中,fobj为待测目标的流量值。
2.3 异常点及斜距归一化处理
在使用SourceExtractor提取流量时会识别到非待测目标的流量信息,从而得到错误的星等值。观测过程中望远镜对目标进行跟踪,目标在图像中的位置相对固定,但是因预报误差其位置会产生变化,因此,在目标轨道预报精确或目标运动速度不快的情况下,可以根据目标在图像中的坐标将错误识别的目标剔除,从而计算得到正确的星等。图4为13日及15日的异常点在CCD中的坐标信息,可以看到一部分点离散在目标坐标区域外,根据这一信息将坐标错误的点剔除。这一方法不能将被恒星污染、云层遮挡这样的情况剔除,而这两种情况下目标的星等值会发生突变,所以可以将距离平均光变曲线0.5星等的数据点FITS(Flexible Image Transport System)图像与在平均光变曲线上数据点的FITS图像进行比对,确认得到的是否是待测目标的光度信息,图4中15日目标坐标区域中的菱形点就是被恒星污染的异常点。
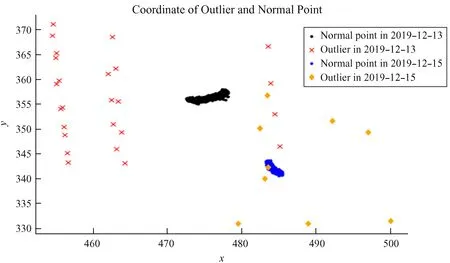
图4 目标异常点坐标分布Fig.4 Outlier of space object′s coordinate distribution
将异常点剔除后得到目标的光度数据,为了去除待测目标斜距对目标光度的影响,需要对得到的星等进行斜距归一化处理[11],通常将卫星斜距归一化到1 000 km处。根据公式
(4)
得到归一化后的星等Muni,其中,Robj为卫星距测站的斜距;Runi=1 000 km。
图5为剔除异常点、斜距归一化后的光变曲线,由图5可见,光度随时间的变化呈现周期性特征,而且在观测时段内星等的变化周期基本保持不变,大致为125 s,整体光变曲线有一个缓慢的变化趋势,这两天的星等有缓慢增大的趋势,曲线振幅在逐渐变大。下一步针对这两条光变曲线进行分析,以确定目标的旋转速率及旋转轴的指向。

图5 观测时段内目标42 968的光变曲线Fig.5 The lightcurve of 42 968 in observation periods
3 火箭体旋转状态分析
火箭体属于空间碎片且运行轨道和姿态不受地面控制。描述火箭体的旋转状态主要包括旋转周期、旋转轴指向和旋转初相位。本节主要根据第2节得到的目标光变曲线确定目标的旋转周期和旋转轴指向,并分析得到的结果。
3.1 会合周期分析
会合周期是一种相对周期,取决于卫星、测站及太阳的位置关系。根据网球拍定理[12]可知,自由刚体逐渐绕着目标最大转动惯量的轴旋转。猎鹰九号火箭末级入轨时间较长(从2017年10月发射至观测时约两年),其几何形状近似为圆柱体,所以可以合理假设目标绕着垂直于目标侧面的轴旋转,对于测站来说,观测到的星等变化周期只是旋转周期的一半,故会合周期大约是250 s。为了更加精确地确定会合周期,本文采用相位离散最小化方法(Phase Dispersion Minimization, PDM)[13]将数据点分段进行分析得到最优解。相位离散最小化的原理是将观测数据按试验周期计算,根据试验周期计算相位矢量,将相位矢量按(0, 1)区间划分为不同的子区间,计算子区间与整个区间的数据方差,使得两者之比最小的试验周期即最精确的会合周期。
空间目标的离散观测值可以分为两个矢量:星等矢量m及观测时间矢量t,其中,第i个观测点
可以表示为(mi,ti),假设在一个观测时段内共有N个观测离散点,即i=1, 2, …,N,则星等矢量m的方差σ2为
(5)


(6)
假设P为试验周期矢量,P中的元素为pk,根据试验周期计算时间矢量t的相位矢量φ。对于相位矢量Φ中的每个元素
(7)

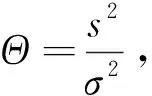
Θ≈1;如果pk是正确的周期,Θ在试验周期内会达到最小值,且趋近于0。
由火箭体的光度数据,t为观测时段的时间点,m为观测时段的目标星等值,会合周期大约为250 s,所以试验周期矢量P为200~300,步长取0.1,相位间隔步长取0.1,即将(0, 1)区间划分为10个子区间,使用上述参数及相位离散最小化方法计算得到更为准确的火箭体会合周期。
图6为两个观测时段内试验周期及通过相位离散最小化方法计算得到的试验周期对应的Θ值。由图6(a)可以发现,在试验周期内存在一个极小值点,13日在Θ最小处对应的周期为249.230 s,由图6(b)可以得到15日在Θ最小处对应的周期为248.290 s。

图6 火箭体会合周期分析Fig.6 Analysis of Rocket Body′s Synodic Period
3.2 旋转轴指向分析
空间目标的旋转状态包含旋转周期及旋转轴指向,通过相位离散最小化方法得到会合周期,观测目标的星等变化周期比较稳定且相对于测站及太阳的相位角变化不大,所以该目标的会合周期可近似看作旋转周期。
在赤道惯性坐标系下,旋转轴以矢量P表示,转化为赤经α、赤纬δ为
(8)
在分析旋转轴指向前需要建立目标光度模型。火箭体本身并不发光,而是反射太阳光,测站观测到的目标图像其实是火箭体的反射光,与目标的表面材料、形状和太阳-目标-测站之间的几何关系有关,三者的几何关系如图7,其中,uobs和usun分别为目标到地球和太阳的方向单位矢量,un为目标表面面元的法线方向单位矢量,uobs和usun之间的夹角即相位角[14]iPA,uh是相位角平分线方向单位矢量。由目标的双行根数得到位置信息,13日的双行根数历元为2019-12-12T18:50:17Z,15日的双行根数历元为2019-12-14T10:29:09Z,太阳的位置信息由喷气推进实验室的DE430星历给出,测站位置为(25.029 9 N,102.797 4 E),海拔高度为1 991.83 m。将这三者的位置转换到惯性系下表示为位置矢量,根据三者的位置矢量可求出uobs,usun,则相位角

图7 太阳-目标-测站之间的几何关系Fig.7 The geometry relationship of sun-space object-observation station
(9)
观测时段内相位角的变化如图8。

图8 观测时段内目标相位角变化曲线Fig.8 Variation trend of object′s phase angle in observation period
火箭体的形状可看作圆柱体,根据此假设可以计算火箭体的等效面积。假设太阳光在火箭体表面为漫反射[15],圆柱体侧面的法线方向定义为圆柱的上下底中心连线,向上底方向为正,圆柱体侧面面元的法线方向为垂直于面元方向向外,对圆柱体侧面面元积分就可以得到侧面的等效面积。太阳入射角为isun,卫星-测站方向矢量与法线方向矢量夹角为iobs,则圆柱体侧面等效面积为
(10)
其中,θ满足
(11)
其中,Acy为圆柱体侧面面积;φ为圆柱体柱坐标系的方位角参数;h为圆柱体高度;d为圆柱体底面直径。
圆柱体上下两底可近似看作平面,平面的等效面积为
Aplea=Aplcosisuncosiobs.
(12)
不考虑下底的火箭体喷嘴,火箭体上下底的法线方向分别沿着上下底平面从里向外,使用(12)式分别计算火箭体上下底的等效面积,根据火箭体侧面及上下底的等效面积就可以确定火箭体的等效面积,从而计算目标的模型光度。
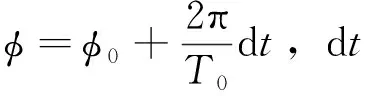
以13日的数据为例,已知Δ0=0°,Δ1=90°,T0=249.23 s,遍历3个参数:λ0∈[0, 360],步长为2;θ0∈[0, 180],步长为1;φ0∈[0, 360],步长为10。每次循环计算观测时段内观测星等与模型星等之差的方差,遍历所有参数后得到总体方差分布,以φ0划分共有36个观测值与计算值之差(O-C)的方差分布图,在每个方差分布图中横坐标表示旋转轴指向λ0,纵坐标表示旋转轴指向θ0,每张O-C方差分布图有两个方差极小值区域,分别位于每张子图中的左下方及右上方,且关于中心点对称。这是由于建立光度模型时,假设火箭体上底及下底面积相等导致的对称性,根据这一推论可知在两个方差极小值区域分别存在使得方差最小的参数组合,在每个方差极小值区域内有两个最小方差收敛区域,O-C方差最小值点在其中一个方差收敛区间内。
计算每张等高线图内最小方差及所对应的(λ0,θ0,φ0)组合,得到36个最小方差点,在这36种组合中选择最小方差对应的组合:(λ0,θ0,φ0)=(212, 116, 120)。图9(a)给出了最小方差组合对应的方差分布图,等高线颜色越接近蓝色表示方差越小,越接近红色表示方差越大。根据O-C方差的对称性可知,在方差分布图的左下方也应存在使得O-C方差最小的参数组合,计算关于左下方差极小值区域O-C方差最小值的参数组合,得到图9(b),方差极小值点对应的参数为(λ0,θ0,φ0)=(32, 64, 290),处于O-C方差收敛区间内。
将以上得到的两个参数组合分别代入光度模型,并比对模型光变曲线和观测光变曲线,比对结果如图10。图10(a), (b)分别对应图9(a), (b)得到的参数,图中标识了每个参数组合对应的O-C方差值,可以发现图10(a)O-C方差值更小,(b)的方差与(a)的方差相差不大并且目标星等的变化趋势也很好地拟合出来。从图10(a)可以看到,光度模型拟合了火箭体光度整体的变化趋势,包括振幅逐渐变大的趋势及每个周期星等极大值点的变化,不过对于每个周期星等极小值点处的光度突变光度模型并没有很好地拟合,这一部分的突变可能由于火箭体侧面镜反射导致的,而光度模型只考虑了目标漫反射的情况。

图9 13日O-C方差分布等高线图Fig.9 Distribution of variance between observation value and calculate value′s difference in 2019-12-13
根据以上分析可以确定编号为42 968的目标旋转轴指向可能包含两种组合,分别是(λ0,θ0)=(212, 116)及(λ0,θ0)=(32, 64),对应的旋转初相位分别是120°,290°,两者之差为170°,而且求得的两个旋转轴指向赤纬λ0相差180°,两个余纬θ0与90°之差的绝对值都为26°,正好对应了光度建模时火箭末级上下底面积相等而导致求得的两个旋转轴指向关于惯性系原点对称的情况。
4 结 论
本文通过分析猎鹰九号火箭体的光变曲线确定其旋转状态,根据2019年12月13日和15日实测的数据得到目标光变曲线存在明显的周期性,说明目标的运动姿态较为稳定。由于在两天的观测时段内目标相位角的不同造成了归一化处理后的目标绝对星等的细微差别。由光变曲线的周期并通过相位离散最小化方法确定了目标的会合周期:13日目标的会合周期为249.23 s,15日目标的会合周期为248.29 s,在两天的时间里目标的周期并没有发生明显的变化。通过建立光度模型的方法计算目标的模型星等,搜寻旋转轴指向和旋转初始相位,以模型星等与观测星等之差的方差最小为判据,确定目标的旋转轴指向。本文计算了13日的O-C方差,由于模型假设火箭体的上底及下底面积相等,所以得到了两个可能的旋转轴指向,分别为(λ0,θ0)=(212, 116)及(λ0,θ0)=(32, 64),若要更加精确地确定旋转轴指向还需更多的观测数据并完善光度模型。

