基于系列斑点图像的视宁度估算精度方法研究*
胡 钢,向永源,刘 忠,王新华
(1. 中国科学院云南天文台,云南 昆明 650216;2. 中国科学院大学,北京 100049)
大气湍流是降低地面大型光学望远镜成像质量的主要因素之一,它使图像在像面发生随机抖动、畸变和破碎。为描述大气湍流对成像过程的影响,基于柯尔莫哥洛夫(Kolmogorov)关于大气湍流的统计模型,文[1]引入了视宁度参数r0,又称为弗里德(Fried)参数,或者大气相干长度。根据定义,视宁度表征地面望远镜实现衍射成像的极限口径[2],也代表大气湍流的剧烈程度。视宁度在选址和高分辨成像等领域有重要意义,比如斑点干涉术[3]的理论传递函数模型与视宁度有关[4],自适应光学中夏克-哈特曼(Shack-Hartmann)波前传感器微透镜阵列的数量由视宁度决定[5]。
估算视宁度的方法有多种,有些需要使用专门的仪器,比如利用北极星星轨的横向抖动方差估算视宁度[6-8];利用探空气球或者声雷达测量不同高度大气的温度结构常数推算大气视宁度[9-10];利用刀口前后焦面光强的变化程度推算视宁度[11];利用干涉仪中被大气干扰的星像干涉条纹推算视宁度[2];利用望远镜上两个间距超过r0的子孔径的差分到达角方差推算视宁度[12];利用星像闪烁的程度推算视宁度[13-14]等等。有些可以利用望远镜观测过程中的斑点图[3,5,15](曝光时间在大气相干时间量级的短曝光图像)估算,比如将一组点源星像的实际平均长曝光或者平均短曝光传递函数[1]与对应的理论传递函数比较从而推导视宁度[16];通过将一组图像的实际谱比值与理论值比较得到视宁度[17](在扩展源图像的高分辨重建领域应用广泛,本文称为谱比法);利用大气湍流对图像对比度造成的变化反推视宁度[18];直接利用点源目标长曝光星像的半高宽(Full Width at Half Maxima, FWHM)估算视宁度[12,19];利用星像在像面抖动的方差估算视宁度[20](本文称为像运动法)等等。
在诸多方法中,半高宽法和像运动法可以较为方便快捷地估算视宁度参数,应用十分广泛。当望远镜受跟踪误差、风或者机械振动等因素(以下统称为综合因素)影响时,这两种方法的结果往往受到影响,从而降低视宁度的估算精度。
本文介绍半高宽法估算视宁度的基本原理,分析其应用条件及综合因素对视宁度估算的影响,并给出应对方法;介绍像运动法的基本原理,跟踪误差等因素的影响并给出应对方法;最后将应对方法应用到实际数据中,并分析结果,将结果与谱比法对照,说明应对方法的有效性。
1 方 法
在等晕区内,大气-望远镜综合系统可以看作一个线性空不变系统,短曝光成像过程在空域和频域可以表示为
i(x)=o(x)*s(x) ,
(1)
I(q)=O(q)S(q) ,
(2)
其中,i(x)为短曝光图像;I(q)为对应的频域;o(x)为目标;O(q)为目标的傅里叶变换;s(x)为点扩散函数,对于点源目标,i(x)=s(x);S(q)为短曝光大气-望远镜综合系统的传递函数;q为归一化空间频率;*表示卷积。
短曝光大气-望远镜综合系统的传递函数又可以分解为望远镜的传递函数和短曝光大气的传递函数之积:
S(q)=T(q)B(q) .
(3)
1.1 半高宽法
半高宽法的本质是利用点源单星长曝光图像的半高宽与视宁度参数之间的简单关系:
(4)
其中,λ为波长。长曝光图像可以通过多张短曝光图像的统计平均获得[21],因为长曝光星像的强度分布近似为高斯函数[15],常常使用高斯函数拟合计算半高宽[8,22],高斯函数的半高宽与标准差存在简单关系:
(5)
分析长曝光大气-望远镜综合系统分辨率与大气分辨率的比值随D/r0的变化情况,分辨率定义为在频率域对调制传递函数(Modulation Transfer Function, MTF)积分[1-2,23],当望远镜口径D远大于视宁度r0时,系统分辨率接近大气分辨率,因此,当D≫r0时,长曝光综合系统的传递函数等于长曝光大气的传递函数,即
(6)
其中,〈·〉表示系综平均;α=r0/D;LE表示长曝光。
为了获取空域长曝光点扩散函数〈s(x)〉LE的半高宽,需将(6)式做逆傅里叶变换,再取其半高宽,但是,普通方法难以得到(6)式的解析解,一种近似方法是用2次方替代5/3次方,用高斯函数近似传递函数,可得到半高宽的解析式(4)。
根据上述分析,(4)式的推导过程实际上做了两处近似:(1)用大气的传递函数代替系统的传递函数;(2)用2次方替代5/3次方。为了说明两处近似在何种程度上影响(4)式的准确度,我们使用数值方法计算理论上系统长曝光点扩散函数的半高宽,然后与(4)式的半高宽比较,结果如图1。图1说明,当D≫r0时,(4)式才能达到较高的准确度,比如当D=1 m,r0=10 cm时,半高宽比值可以达到0.93,说明对于口径1 m级的望远镜,(4)式理论上能够达到较高的准确度,因此,本文使用(4)式估算视宁度。

图1 (4)式半高宽与综合系统的半高宽的比值随D/r0的变化情况Fig.1 Ratio of FWHM calculated by equation (4) and theoretical FWHM of the synthetic system as a function of D/r0
上述分析是基于理想望远镜的假设,即无像差、跟踪误差和风载荷影响,支撑系统完全刚性等。实际上,这些因素都会使长曝光点源星像偏大,从而使得(4)式估算的视宁度偏小。
当受到综合因素影响时,长曝光图像往往在某个方向上延展,强度分布表现出类椭圆形,因此选择合适的方向计算半高宽变得尤为重要。应对方法是使用二维高斯函数拟合受到综合因素影响的长曝光点源单星图像,将方差最大的方向视为受到影响较大的方向。二维高斯函数为
(7)
对应的协方差矩阵为
(8)
绝大多数情况下,相关系数ρ不为0,协方差矩阵不是对角矩阵,需将协方差矩阵化为对角矩阵以确定受影响较大的方向,再取与之垂直方向的方差即对角矩阵中较小的方差计算半高宽,进而使用(4)式估算视宁度,如图2。
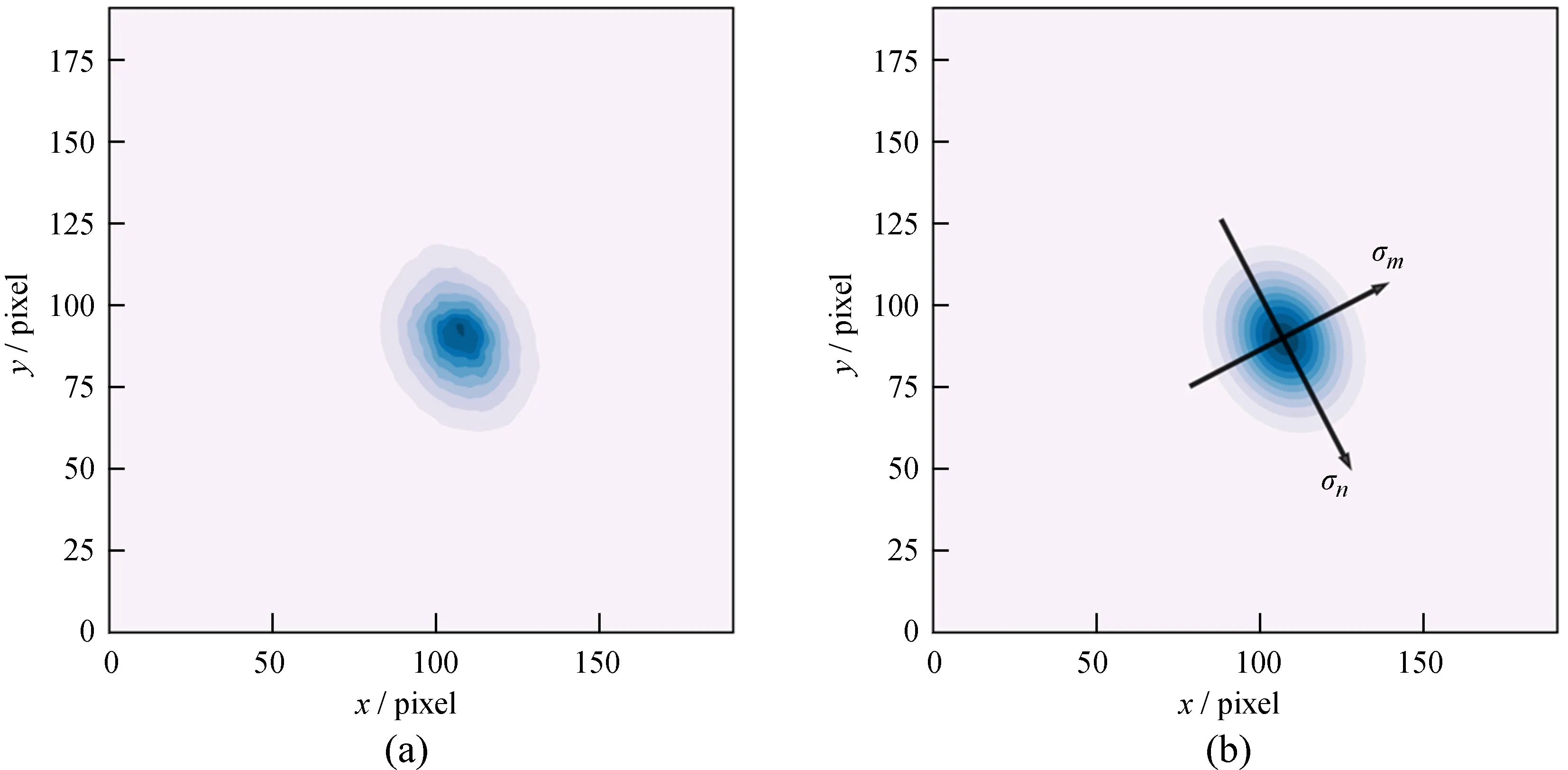
图2(a)一张受到综合因素影响的点源单星的长曝光图像;(b)拟合长曝光图像的二维高斯函数图像Fig.2 (a) A long exposure image affected by tracking error, wind or mechanical vibration;(b) A two dimensional gaussian function that fits the left long exposure image (Right)
1.2 像运动法
大气湍流对成像过程的一种影响是改变瞳面的波前到达角,造成像面图像的随机抖动,因此,测量图像抖动的剧烈程度可以间接推导视宁度参数r0。文[20]给出了r0与波前到达角方差之间的关系
(9)

(10)
其中,x,y为某像素坐标位置;I(x,y)为(x,y)坐标处的像素值;X,Y为重心坐标位置。
像运动法会受综合因素的影响。假设仅存在大气湍流时图像重心位置为XA,综合因素造成的偏移量为XV,且XA与XV相互独立,则实际重心位置为X=XA+XV,可以得出实际重心位置的方差DX=DXA+DXV,则DX≥DXA。因此,一般来说,综合因素会造成图像抖动方差增大,从而使得估算的视宁度偏小。
像运动法估算视宁度的精度也受图像曝光时长的影响[26-28],理想情况下,曝光时长小于或等于大气相干时间,不同斑点图对应不同状态的 “冻结” 的大气,图像重心位置不一样。当每张图的曝光时长增加时,重心位置会被平滑,从而降低重心位置抖动的方差,造成估算的视宁度偏大。
需要指出的是,望远镜口径也对像运动法估算视宁度的精度造成影响。文[26]认为,像运动实际上是由大于口径的湍流元胞造成的,小尺度的湍流尽管会造成图像的斑点结构,但是口径内众多的小尺度湍流会平滑重心位置,造成重心位置偏移不明显。文[18]使用40 cm口径的望远镜估算视宁度,结果显示,像运动法估算的视宁度是对比法的1.4倍;文[29]使用65 cm口径的望远镜估算视宁度,结果显示,像运动法的结果是谱比法的1.5倍;文[8]使用50 cm口径的望远镜对比了星轨法(本质上是像运动法)与差分像运动仪(Differential Image Motion Monitor, DIMM),发现星轨法的结果偏大。这些研究表明,像运动法估算视宁度时,大口径望远镜的结果偏大。
(9)式是根据柯尔莫哥洛夫谱推导的,没有考虑大气湍流外尺度的影响,实际上,冯卡尔曼(Von Karman)谱的数值模拟表明,当考虑有限外尺度时,重心的抖动方差偏小,导致估算的视宁度偏大。

图3 门限大小对视宁度估算的影响Fig.3 Influence of threshold on seeing estimation
文[30]分析了CCD噪声对重心位置的影响,发现重心位置抖动方差与窗口大小呈四次方关系,是严重的影响因素,设置门限在某种意义上限制了窗口大小,加窗法则直接将窗口限制在某个较小的范围内。
本文将加窗法与门限值法相结合,首先以图像最大值为中心,以WD为直径加窗,WD定义为使用高斯函数近似点扩散函数之后,强度值下降为最大值的1/e时的直径,类似于衍射受限点扩散函数的均方根宽度的定义[31],理论上,WD≈1.2FWHMpsf。随后,考虑到文[32-33]模拟分析发现以3倍的读出噪声作为门限可以有效降低读出噪声的影响,本文也以3倍的读出噪声作为门限计算重心位置,读出噪声可以从一系列暗场图像中分析获得。
当受到综合因素影响时一系列点源单星斑点图的重心位置往往在某个方向延展,使得这个方向上的抖动方差大于其他方向。应对策略是利用主成分分析法找到一组重心坐标中方差最大的方向,即第一主成分,将此方向看做受到影响较大的方向。将坐标数据降维在第二主成分方向上(与第一主成分正交的方向),并计算方差,然后利用方差估算视宁度。在图4的情况下,取方向的方差估算视宁度。

图4 一系列斑点图重心坐标位置及第一主成分方向和第二主成分方向Fig.4 Coordinates of center of gravity of a series of speckle images and directions of the first and second principle component
主成分分析法是一种应用广泛的数据降维方法,在天文数据处理领域也有应用[34],一般是将数据降维到前n阶方差最大的方向,以保留原始数据的主要信息特征,本文是将二维的重心位置坐标降维到方差小的方向,具体的算法实现如下。
(1)将所有重心坐标组成矩阵
(11)
(2)将X每一行进行零均值化
(12)
(3)计算协方差矩阵
江苏省常熟市农村垃圾治理采取“村—镇—市”三级转运模式,管理方面主要包含组织规划、资金保障、监督管理和宣传推广4个维度,垃圾问题得到极大缓解。
(13)
(4)将协方差矩阵C对角化为C′;
(5)C′中对角线的元素即为第一主成分和第二主成分方向的方差,值小的方差即为所需要的方差。
尽管选取方差小的方向估算视宁度,但是此方向并非完全不受任何影响,因此有必要限制一组斑点图的拍摄时间,因为拍摄时间长,风向等因素可能发生剧烈变化,导致各个方向都受到影响。判断所选择的方向是否受到较大干扰的方法是将重心坐标在第二主成分方向的投影以直方图的形式表示,并使用高斯函数拟合,考察其决定系数,因为当不存在任何影响时,重心位置的变化应符合高斯分布,受影响较小的方向也应符合高斯分布。实际应用中可以限制决定系数,比如当决定系数大于0.8时才使用本文的方法,否则放弃使用该组图像估算。图5为一组斑点图在第二主成分上投影的直方图。

图5 在第二主成分方向上投影的重心坐标以及拟合的高斯函数Fig.5 Coordinates of center of gravity projected on the second PCA direction and fitted Gaussian function
1.3 谱比法
谱比法由文[17]提出,是通过计算一组图像平均频谱的平方与平均能谱的比值,再将此值与理论值比较,对于给定的望远镜,理论值仅是视宁度的函数,表达式为
(14)
其中,〈S(q)〉既可以是平均长曝光传递函数也可以是平均短曝光传递函数,表示平均短曝光传递函数时,意味着将所有图像先按照重心对齐再做计算,因此可以不受跟踪误差等因素的影响,此时理论表达式为
(15)
平均能谱的理论表达式为
(16)
其中,
(17)
(18)
(19)

2 数据处理与分析
2.1 数 据
为验证本文应对综合因素影响的方法的有效性,我们采用两组实测数据进行试验。
第1组数据是2014年9月12日晚UT 18:48:28到UT 19:12:03,抚仙湖1 m新真空太阳望远镜拍摄的25组数据,每组数据含200张斑点图,详细信息如表1。

表1 1 m新真空太阳望远镜实验参数Table 1 Experiment parameters of NVST
第2组数据是2009年2月9日晚UT 12:49到UT 20:46,丽江观测站2.4 m望远镜对10个目标拍摄的95组图像,每组500帧,详细信息如表2。

表2 2.4 m望远镜实验参数Table 2 Experiment parameters of 2.4 m telescope
对所有图像按照文[35]的方法进行预处理。对于1 m新真空太阳望远镜的每一组数据,以任意一张图(本文选取第1张图)的最大值为中心,为了消除非等晕效应的影响,加快处理速度,将图像裁剪成192×192像素的子图。对于2.4 m望远镜的数据,因为图像已经是以5.376×5.376″的子图读出的,因此不用再做裁切处理。图6是经过预处理得到的斑点图。

图6(a)校准完成的1 m新真空望远镜拍摄的斑点图;(b)校准完成的2.4 m望远镜拍摄的斑点图Fig.6(a) a frame of calibrated speckle image taken by NVST;(b) a frame of calibrated speckle image taken by 2.4 m telescope
2.2 处理与分析
对数据采用以上3种方法进行处理,详细处理流程如图7。对半高宽法,预处理完成后,直接将所有斑点图叠加,等效为单张长曝光图像,再对图像使用二维高斯函数拟合,并使用上述方法找到合适方向的半高宽从而估算视宁度。对像运动法,预处理完成后,计算所有图像重心坐标,并使用主成分分析方法将重心坐标投影到第二主成分上,以直方图表示该方向的重心坐标,计算决定系数R2,如果决定系数大于0.8就使用该方向的方差估算视宁度,否则不使用这组图像,这个条件也应用于半高宽法。对于谱比法,预处理完成后,将所有点源单星图像按照重心对齐,以对齐后的图像计算平均短曝光频谱与平均能谱得到实际谱比值,与理论谱比值比较,找到最为接近的视宁度参数值。
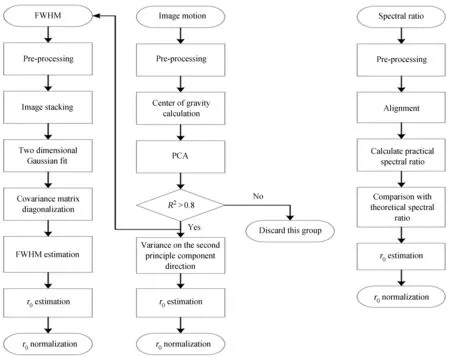
图7 3种方法的流程图Fig.7 Flowchart of three methods
为了方便比较,将所估算的r0全部归算到天顶距为0°、波长为500 nm时的值,归算公式为
(20)

作为对比,本文同时使用以上应对综合因素的修正方法和选取任一方向的方差估算视宁度(本文选取纵向方差)。对于1 m新真空太阳望远镜的数据,使用纵向方差估算的视宁度如图8,使用修正方法估算的视宁度如图9;对于2.4 m望远镜的数据,使用纵向方差估算的视宁度如图10,使用修正方法估算的视宁度如图11。

图8 1 m新真空太阳望远镜数据:点划线是在半高宽法中使用纵向半高宽估算的视宁度,虚线是在像运动法中使用纵向方差估算的视宁度,实线是使用谱比法估算的视宁度Fig.8 NVST data: Dash-dotted line shows seeing parameter estimated by using longitudinal FWHM in the FWHM method, dotted line shows seeing parameter estimated by employing longitudinal variance in the Image Motion method, solid line shows seeing parameter estimated by spectral ratio technic
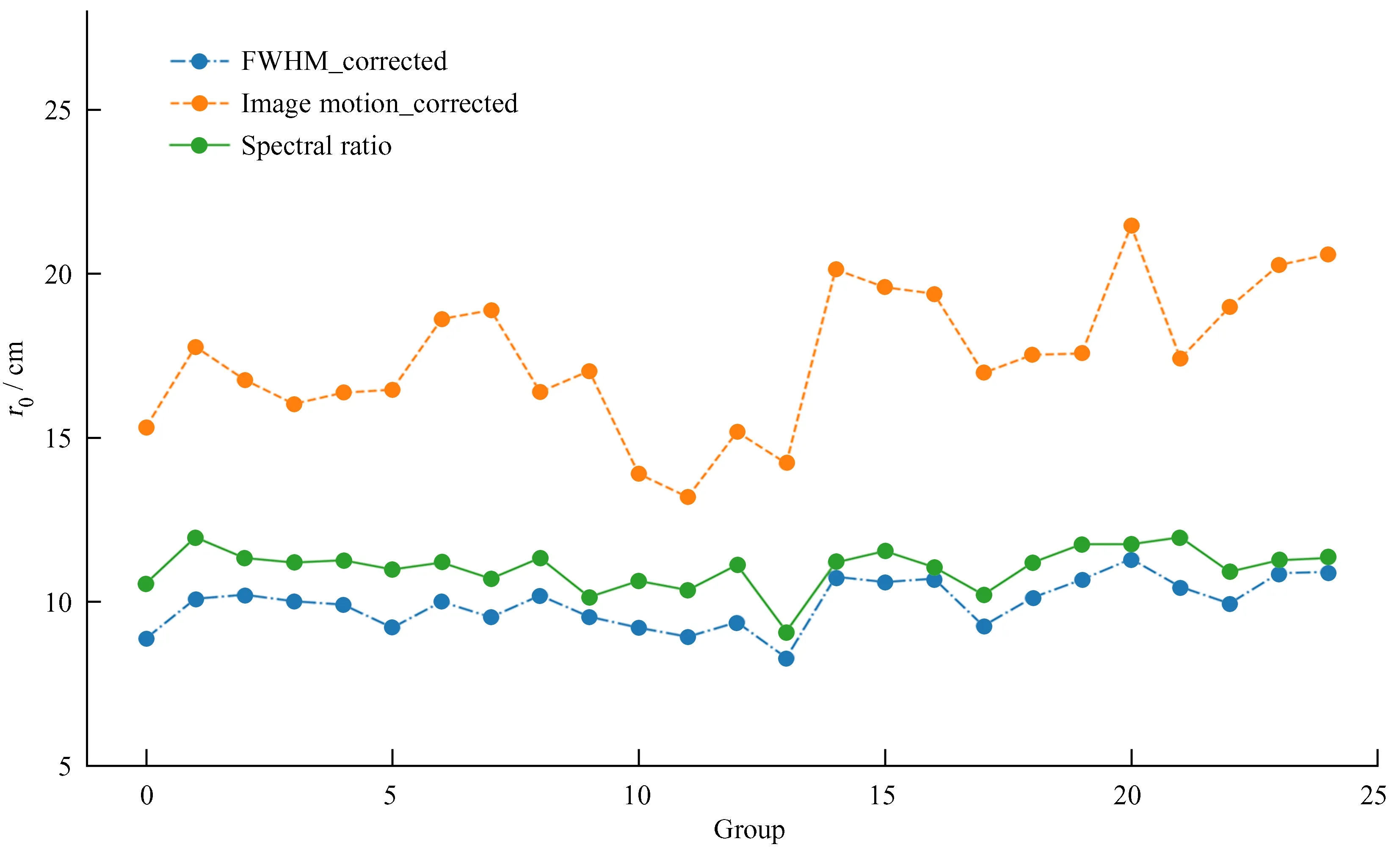
图9 1 m新真空太阳望远镜数据:点划线是使用修正的半高宽法估算的视宁度,虚线是使用修正的像运动法估算的视宁度,实线是使用谱比法估算的视宁度Fig.9 NVST data: Dash-dotted line shows seeing parameter estimated using corrected FWHM method, dotted line shows seeing parameter estimated by corrected Image Motion method, solid line shows seeing parameter estimated by spectral ratio technic
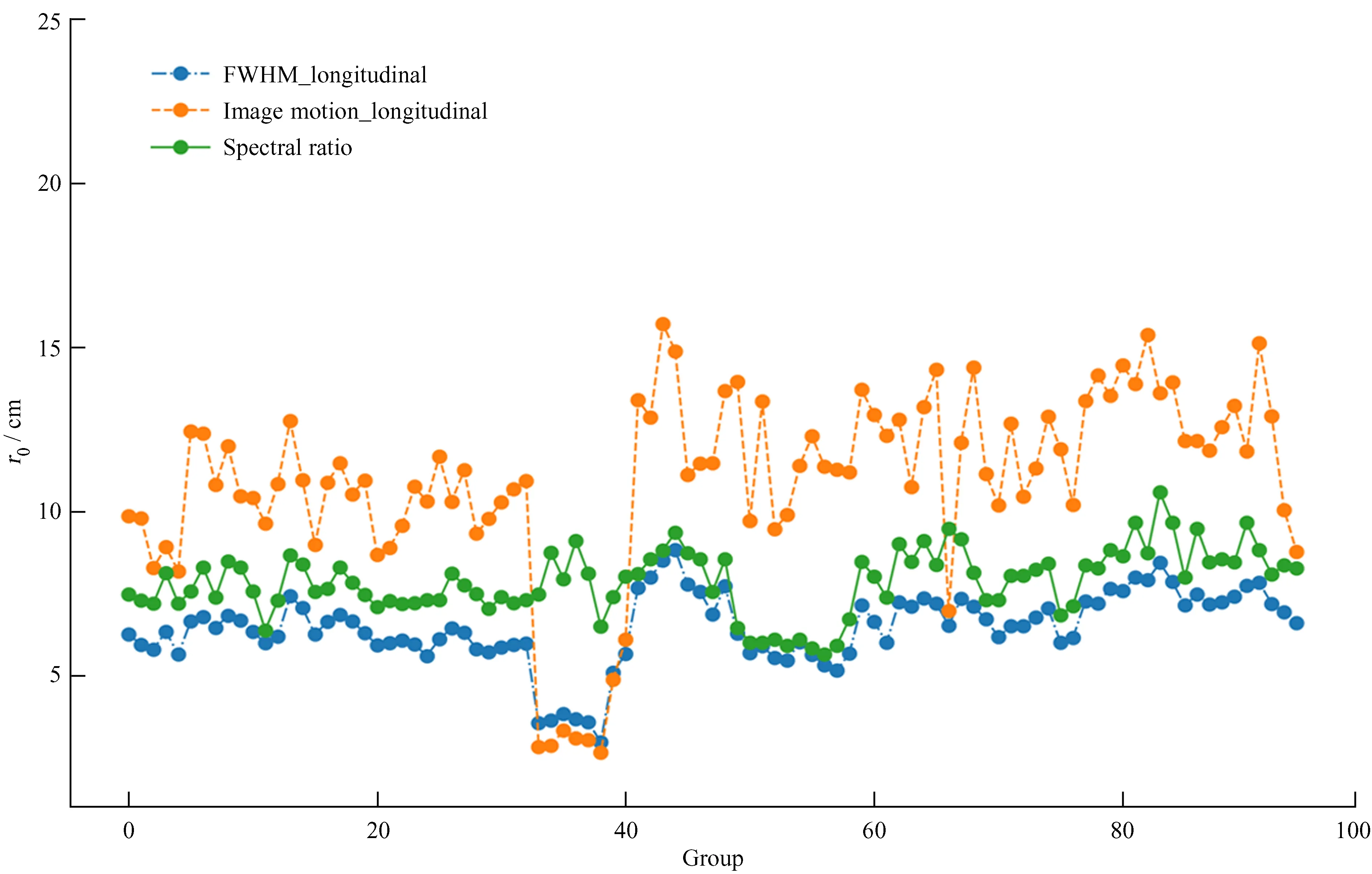
图10 2.4 m望远镜数据:点划线是在半高宽法中使用纵向半高宽估算的视宁度,虚线是在像运动法中使用纵向方差估算的视宁度,实线是使用谱比法估算的视宁度Fig.10 2.4 m telescope data: Dash-dotted line shows seeing parameter estimated by using longitudinal FWHM in the FWHM method, dotted line shows seeing parameter estimated by employing longitudinal variance in the Image Motion method, solid line shows seeing parameter estimated by spectral ratio technic
图9显示,对于1 m新真空太阳望远镜的数据,在观测时间段内,使用半高宽法得到的r0均值为9.96 cm,标准差为0.73 cm;像运动法得到的r0均值为17.44 cm,标准差为2.12 cm;谱比法得到的r0均值为11.04 cm,标准差为0.62 cm。图11显示,对于2.4 m望远镜的数据,使用半高宽法得到的r0均值为7.13 cm,标准差为0.82 cm;像运动法得到的r0均值为13.48 cm,标准差为2 cm;谱比法得到的r0均值为7.88 cm,标准差为0.97 cm。
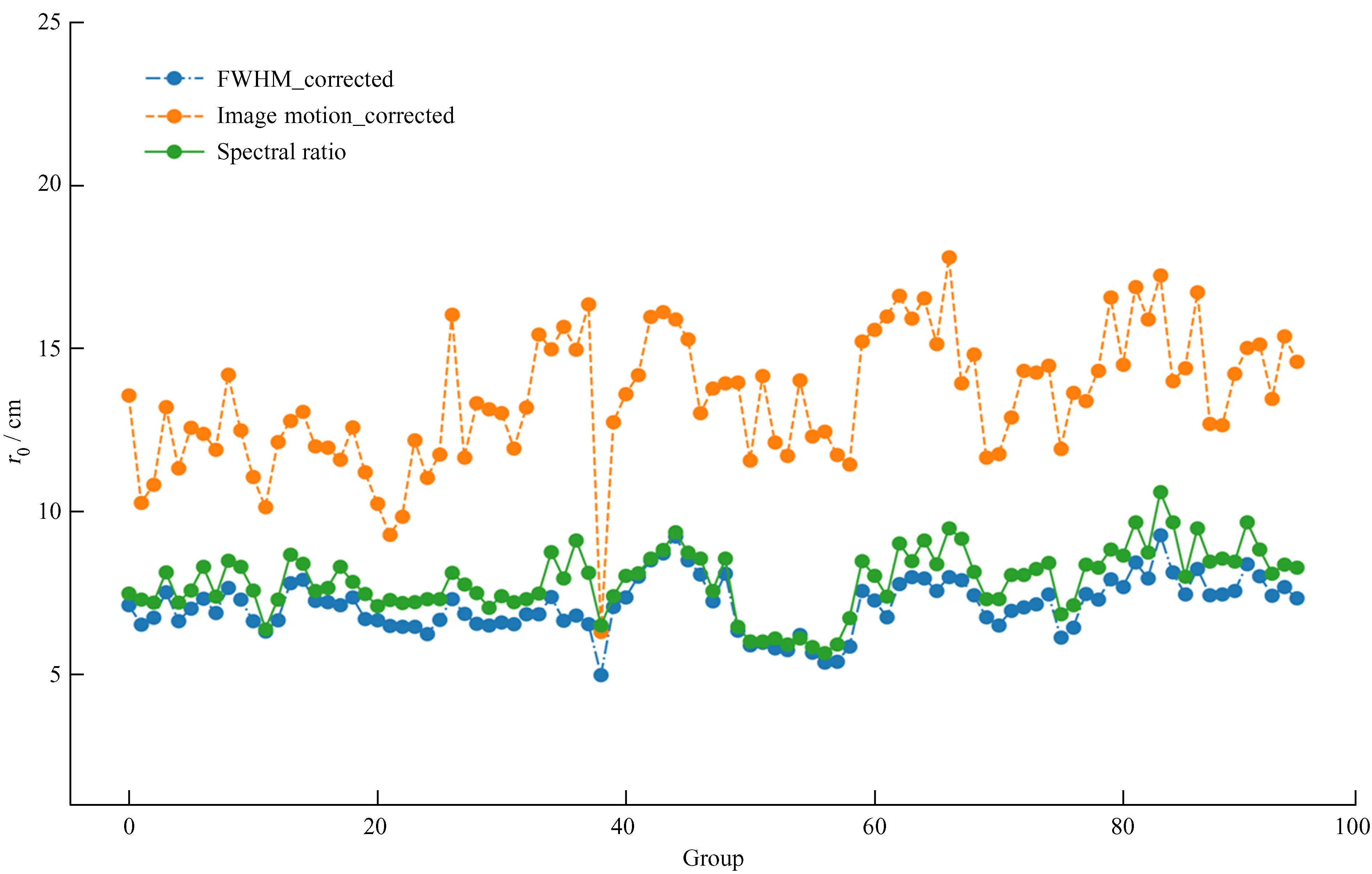
图11 2.4 m望远镜数据:点划线是使用修正的半高宽法估算的视宁度,虚线是使用修正的像运动法估算的视宁度,实线是使用谱比法估算的视宁度Fig.11 2.4 m telescope data: Dash-dotted line shows seeing parameter estimated using corrected FWHM method, dotted line shows seeing parameter estimated by corrected Image Motion method, solid line shows seeing parameter estimated by spectral ratio technic
由图8~图11可以得到看出:
(1)半高宽法估算的视宁度比谱比法偏小,可能的原因有:① (4)式的推导过程使得r0值稍微偏小;② 望远镜像差、残余的跟踪误差、风或者机械振动等因素使得半高宽偏大,从而使估算的视宁度更偏小。
(2)像运动法估算的视宁度比谱比法偏大,可能的原因有:① 曝光时间过长,导致实际测量的像运动方差偏小,造成估算的视宁度偏大;② 望远镜口径过大,像运动更多反应大于口径的湍流元胞的起伏;③ 没有考虑有限外尺度的影响;④ CCD噪声和光子噪声对重心抖动方差计算的影响。
(3)纵向方差估算的r0比修正法估算的r0偏小,这是因为纵向方差包括跟踪误差、风或者机械振动等因素的影响而偏大,使得估算的r0值偏小。
(4)对于1 m新真空太阳望远镜的数据,修正的半高宽法估算的视宁度与谱比法之间的相关系数为0.79,纵向半高宽估算的视宁度与谱比法之间的相关系数为0.39;修正的像运动法与谱比法之间的相关系数为0.52,纵向方差估算的视宁度与谱比法之间的相关系数为-0.01。对于2.4 m望远镜的数据,修正的半高宽法估算的视宁度与谱比法之间的相关系数为0.91,纵向半高宽估算的视宁度与谱比法之间的相关系数为0.58;修正的像运动法与谱比法之间的相关系数为0.65,纵向方差估算的视宁度与谱比法之间的相关系数为0.24。这说明在一定时间内,当一系列斑点图受到综合因素的影响,而本文选取的方向并未受到严重影响时(最低要求决定系数大于0.8),使用本文的方法可以有效提高半高宽法、像运动法与谱比法之间的相关性,对比任意选择一个方向估算视宁度,本文的方法可以有效提高半高宽法和像运动法的视宁度估算精度。
3 总结与展望
本文分析了影响半高宽法和像运动法估算视宁度精度的各种因素,提出了一种可以改善跟踪误差、风或者机械振动等因素影响的方法,并使用实测数据进行了验证,得到以下主要结论:
(1)使用半高宽法估算视宁度时,更大口径的望远镜有利于提高视宁度的估算精度;
(2)像运动法估算的视宁度比谱比法偏大,可能的原因有曝光时间过长、望远镜口径过大、有限外尺度的影响和CCD噪声或者光子噪声的影响;
(3)一系列斑点图受到跟踪误差、风或者机械振动等因素的影响,表现为在某个方向上延展时,使用本文的方法选择合适的方向估算视宁度,可以有效改善跟踪误差、风或者机械振动等因素的影响。方向选择的依据是:① 此方向上的方差小;② 重心坐标投影在此方向上依然较好地符合高斯分布。
本文提出的方法改善了跟踪误差、风或者机械振动等因素对半高宽法、像运动法的影响,提高了半高宽法、像运动法和谱比法之间的相关性。但是,这3种方法估算的视宁度之间仍然存在一定的偏差,分析偏差的影响因素,量化影响因素与偏差程度之间的关系,以及补偿偏差的方法是未来工作的重点。

