基于文化基因算法和犹豫模糊集的聚类算法及其分布并行实现

王 超 英

(东莞职业技术学院 广东 东莞 523808)

0 引 言

随着医院的信息化建设和普及，全国的医疗系统每天产生海量的数据，如何高效地管理医疗大数据成为了一个难题[1]。在医学领域存在大量的高维小样本数据，例如医嘱类文档数据、病例类文档数据、DNA微阵列数据[2-3]。海量高维小样本数据集的聚类和分析需要大量的处理时间。以DNA微阵列数据为例，微阵列的维度高，且含有大量的冗余样本和不相关样本，严重影响聚类器的准确率[4]。

通过特征选择处理能够降低特征集的维度，删除冗余特征和不相关特征，有助于提高数据聚类的准确率和速度，是当前高维小样本数据挖掘领域的研究热点[5]。为了解决上述高维小样本数据集的瓶颈问题，许多研究人员进行了深入的分析[6]。文献[7]基于随机森林变量重要性分数提出了一种加权K-均值的基因微阵列数据聚类算法，以基因为对象、样本为特征、基因的重要性分数为权重进行K-均值聚类，该算法提高了聚类结果的同质性和差异性。文献[8]提出的高维微阵列数据混合特征选择算法分为两层：第一层使用信噪比方法计算全部基因的信噪比值，根据信噪比值选择指定数目的信息基因，过滤无关基因；第二层使用改进的Lasso方法对第一层得到的信息基因候选子集进行特征选择，剔除冗余基因。文献[7-8]均采用了过滤式特征选择算法，分别将随机森林变量重要性分数和基因信噪比作为特征重要性的评价指标，此类传统方法难以获得最少的特征数量[9]。

DNA微阵列数据存在以下特点[10]：(1) 生物标志物的数量极低(低于1%);(2) 生物标志物能够提高特征子集的聚类准确率;(3) 过滤式特征选择可缩小搜索空间，但无法保证优质的特征选择结果;(4) 样本量少，聚类器训练难度大。提取最少量、最高准确率的特征子集是特征选择的两个目标，采用元启发式算法对两个目标进行寻优是一个重要的研究方向，例如：量子进化算法[11]、飞蛾扑火优化算法[12]和人工蜂群优化算法[13]，但此类算法在全局搜索和局部开发之间未能实现较好的权衡，同时基于迭代的算法对于海量数据的处理速度较慢，效率较低。文化基因算法[14](Memetic Algorithm,MA)是一种基于种群全局搜索和基于个体局部启发式开发的结合体，其搜索效率最高比遗传算法快数个数量级。鉴于递归模型[15]在全局搜索和局部开发之间能够实现较好的平衡，本文将文化基因算法和递归模型结合，设计了递归文化基因算法(Recursive Memetic Algorithm,RMA)。采用递归文化基因算法求解高维小样本数据的特征选择问题，但是基于迭代的寻优过程依然较为耗时。

分布式并行计算模型是加快大数据处理的有效方法，目前的大数据技术大多基于MapReduce框架，但该框架并不适合基于迭代的算法，原因主要有[16]：(1) 每次迭代作为独立任务重新处理，需要重新读写数据和初始化数据；(2) 每次迭代需要重新从分布式文件系统加载程序，消耗I/O资源和CPU资源；(3) 前一次迭代必须全部结束并且数据全部写入分布式文件系统，才能开始下一次迭代。Spark框架[17]则是基于内存的分布式并行计算模型，将数据缓存于各节点的内存中，从而缩短数据访问的延迟。本文基于Spark架构设计和实现了递归文化基因算法，可以高效、准确地进行高维小样本数据集的特征选择处理。并且本文研究并提出了一种基于犹豫模糊集理论(Hesitant Fuzzy Set,HFS)的加权相关性指数度量基因的相似性，设计了基于HFS的密度聚类方法，HFS对噪声具有鲁棒性，设计了迭代Spark框架的弹性分布式数据集(Resilient Distributed Datasets,RDD)模块将基因集聚类处理。

1 犹豫模糊集理论

HFS是一种扩展模糊集，其隶属度不是确定值或服从确定分布，而是多个可能值，该理论对于群决策信息的处理具有优势[18]。

1.1 HFS定义

设X={x1,x2,…,xn}为一个固定集，如果A满足以下条件，则认为A是X的一个HFS。

A={〈x,hA(x)〉|x∈X}

(1)

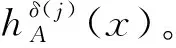
设h、h1、h2为3个HFE，HFE支持以下三个运算：

(2)

(3)

(4)

给定h∈HFE(x)，x的下限和上限分别定义为：

LB:h-(x)=min(h(x))UB:h+(x)=max(h(x))

(5)

设Aenv(h)表示h的包络线，表示为(h-,1-h+)。

1.2 HFS的相关性

设X={x1,x2,…,xn}为一个离散论域，A和B是X上的两个HFS，表示为A={〈xi,hA(xi)〉|xi∈X,i=1,2,…,n}，B={〈xi,hB(xi)〉|xi∈X,i=1,2,…,n}。如果len(hA(xi))

(6)

两个HFS的相关性定义为：

(7)

如果A,B∈HFS，那么CHFS(A,A)=EHFS(A),CHFS(A,B)=CHFS(B,A)。最终可计算出两个HFS的相关系数：

(8)

HFS的相关系数具有以下属性[19]：ρHFS(A,B)=ρHFS(B,A)，0≤ρHFS(A,B)≤1，如果A=B，那么ρHFS(A,B)=1。

2 聚类系统总体结构

本文的高维大数据聚类系统(见图1)主要分为两个部分：基于密度的聚类处理和递归文化基因的特征归简处理。两个部分是递归迭代的关系。在每次迭代中，递归文化基因算法递归地化简特征子集，将特征子集输入聚类处理部分，根据聚类结果判断特征子集的质量，实现了一种封装式特征选择方式。密度聚类处理应用特征子集做聚类处理，基于Spark框架提高处理的速度和效率。

图1 高维大数据聚类系统的主要模块图

3 基于递归文化基因的特征归简

递归文化基因算法(RMA)进行特征选择总体上重复执行文化基因算法(MA)，逐步缩小特征空间。MA采用精英机制，随机建立种群，按聚类的适应度值(准确率)将染色体排列。首先，每个染色体做局部搜索处理，将其替换为更好的染色体；然后，采用轮盘赌选择交叉算子的染色体，应用MA的交叉算子和变异算子。MA算法对于一般数据的特征选择效果较好，但对高维微阵列数据的降维能力较弱，因此设计了RMA模型。

应用MA优化种群，选出适应度高于动态阈值θ的i个最优染色体，i个染色体和β%的最优特征合并组成新的特征空间，新特征子集的聚类准确率应当高于θ;再次应用MA处理上述特征子集，逐渐缩小特征空间，并且提高后续基于密度聚类的准确率。图2为RMA的算法流程。

图2 RMA的算法流程

(1) 局部搜索。初始化阶段将排序的特征集输入RMA做局部搜索处理，局部搜索包括ADD和DEL两个算子。设cr为选择的一个基因子集的染色体，P和Q分别为染色体cr选择和排除的基因子集。ADD算子将Q的基因加入P中，DEL算子将基因从P放入Q中。局部搜索的主要问题是决定ADD、DEL算子的输入基因集，首先采用ReliefF方法[20]将所有的特征排序，然后ADD算子选择Q中最优的特征，加入P中，DEL算子选择P中最差的特征，移至Q中。

(2) 交叉算子。交叉算子是一种遗传算子，交叉算子的方式主要有单点交叉、两点交叉、多点交叉、融合交叉和均匀交叉等，其中两点交叉实现较为简单，且无须设置交叉概率，因此采用两点交叉算子。

(3) 变异算子。变异算子也是一种遗传算子，有助于增强算法的全局搜索能力。变异率设为随机变量q，每次迭代基于概率q应用变异算子。

(4) 综合多目标的适应度函数。基因微阵列的聚类准确率结果作为主目标，特征数量作为次目标。具体方法为：设置一个误差域值，在最大化次目标的情况下，保留其中准确率误差小于阈值的染色体，删除高于阈值的染色体。算法1所示为适应度评价算法，采用加权平均准确率和特征数量决定优质的染色体，其中γ=1-(选择的特征数量/特征总数量)。

算法1适应度评价算法

输入：染色体ci,cj。

输出：优质染色体c。

1. if ((mod(acc(ci)-acc(cj))>α))

//mod表示模运算，acc()为准确率

2. if (acc(ci) >acc(cj))

//比较准确率

3. returnci;

4. else

5. returncj;

6. else

7.v=((w1×acc(ci))+(w2×γ(ci)))-((w1×acc(cj))+(w2×γ(cj)))

8. if (v>0)

9. returnci;

10. else

11. returncj

(5) 特征空间化简。设一个动态阈值φ，种群的top-i染色体与φ作比较，如果染色体的适应度高于φ，则重建种群。通过调节φ将种群规模从100%调节至ρ%，重建种群时，φ设为top-i种群的平均值。算法2是φ的增加算法伪代码，其中：r是种群重建的次数，φ随着r递增，参数l1,l2,l3,step等参数根据实验确定。算法3是φ的衰减算法伪代码，φ随着recn增加而降低。如果处理测试集的特征集较小且准确率高，或者达到了预定义的最大递归次数，则停止递归模型。根据实验结果将li值设为：l1=8,l2=6,l3=3,l4=10,l5=13。

算法2φ的递增算法

输入：top-i染色体的平均准确率：accavg。

输出：动态阈值φ。

1.stepl=step×2；

2. if (r>l1)

3.φ=max(accavg,100-stepl);

4. else if (r>l2)

5.φ=max(accavg,100-2×stepl);

6. else if (r>l3)

7.φ=max(accavg,100-3×stepl);

8. end if

算法3φ的衰减算法

输入：种群重建次数：recn。

输出：动态阈值φ。

试验过程中，每周从每个重复组中随机选出1只小鼠，宰杀解剖后分别切取十二指肠段、空肠段、回肠段各3 cm左右。按照ELISA试剂盒使用说明书通过酶标仪进行测定肠道黏膜SIgA的表达水平。试剂盒购置于德国IBI分装公司。

1. if (recn>l4&&φ≥ρ+step)

2.φ=φ-step;

3. if (recn>l5&&φ≥ρ-step)

4.φ=φ-step;

5. end if

4 基于密度的聚类系统

4.1 聚类算法

设ξ为类的最少成员数量，τ为类内成员之间的最大距离。本文的研究对象为DNA微阵列数据集，所以假设数据元素为基因数据。设Nτ(gi)表示与基因(gi)距离小于τ的基因集，如果(|Nτ(gi)|+1)≥ξ，则称gi为一个核心基因(Core Gene,CG)，|Nτ(gi)|表示Nτ(gi)的大小。类中的非CG基因称为边缘基因(Border Gene,BG)。设G={g1,g2,…,gn}为一个基因集，如果gb∈CG且ga∈Nτ(gb)，那么ga由gb密度直达，将gb由ga密度直达表示为ga→gb，核心基因具有自我密度直达的性质。设一个基因序列为{g1,g2,…,gk}，如果存在一个密度直达序列满足条件gi→gi+1，1≤i≤k-1，那么g1向gk密度可达，表示为g1⟹gk。密度可达具有对称性，即g1⟹gk≡gk⟹g1。如果一个非CG与任意的CG均不是密度可达，那么该基因为孤立基因(Outlier Gene,OG)。CG的邻居基因之间密度相连，并且所有可达基因均与CG密度相连。如果存在gk⟹gi，gk⟹gj，gk∈CG，那么gi和gj密度相连，本文将密度相连表示为gi⟺gj。对于聚类问题，同一个类的基因之间密度相连。

4.2 基于犹豫模糊理论的基因相似性度量

相似性度量是决定聚类准确性的关键因素，采用HFS相关系数度量基因的相似性。设Gj为m个HFS的元素，cor=(ρij)m×m为一个相关矩阵。根据式(8)，ρij表示Gi和Gj间的相关系数，ρij具有以下属性[19]：(1) 0≤ρij≤1,i,j=1,2,…,m；(2)ρii=1,i=1,2,…,m；(3)ρij=ρji,i,j=1,2,…,m。

Gk={〈Col,hGk(Col)〉|Col∈Co,Gk∈G}

(9)

将表达谱值Exp做归一化处理，即{0≤Exp≤1|Exp⊂hGk(Col)}，hGk(Col)是基因Gk在条件hGk(Col)下的犹豫模糊元素，表示为HFE(k,l)。

(10)

WCHFS(Ga,Gb)=

(11)

(12)

5 分布式聚类系统设计

采用基于密度的聚类算法对基因微阵列做聚类处理，基于Spark框架实现对聚类算法的分布式处理。基于Spark框架的分布式聚类算法如图1所示，主要分为5步：① 数据预处理；② 特征归简；③ 计算距离；④ 建立子类；⑤ 最终融合。

Spark框架由1个master模块和若干的worker模块组成。Master为worker分配job，在driver的协助下控制计算程序。worker的job从RDD、分布式文件系统(Hadoop Distributed File System,HDFS)、数据帧(DataFrame)等存储系统读取数据，然后处理剩余数据并输出结果。worker节点的每个job由多个阶段组成，worker串行地完成各个阶段，每个阶段可能独立或者依赖之前阶段的输出。Spark内部将数据分割为若干的分区，每个worker节点处理有权限的部分分区，输出相应的结果。worker节点度量数据的相似性，Spark的平台负责实现分布式处理程序的细节，例如：负载均衡、容错机制、数据分布、寻址处理等。

Spark可独立运行或者建立于Hadoop YARN、Apache Mesos和Amazon EC2等云计算平台。Spark支持分布式数据存储系统，包括HDFS、HBase等。本文在YARN和EC2上建立Spark，采用HDFS作为分布式数据存储系统。

5.1 数据预处理

基因表达数据集的预处理内容主要为：采用表达谱对数变换处理[21]将输入数据集归一化，将一些数据做单位转换和偏差转换处理。如果实验矩阵40%以上的行是空值，那么过滤这种表达谱矩阵。例如：如果{(Ga,Gb)∈HFS,leni(hGa(xi))

每个微阵列实验是一个m×n的矩阵M，m是基因的数量，G=(G1,G2,…,Gm)，n是实验条件的数量，Co=(Co1,Co2,…,Con)。假设共存在q个医学实验，最终共有n个条件下对m个基因的q次实验结果。设置一个Spark driver程序归一化矩阵每行的数据，计算每行数据的均值μ和方差σ。将旧的表达谱替换为新值，计算式表示为：

(13)

5.2 特征归简

采用第3节中基于递归文化基因的特征归简算法缩小特征空间。

5.3 计算距离

加权的HFS相关系数WρHFS(Ga,Gb)表示基因Ga和Gb之间行为的相似性，相关系数越高说明基因行为的相似度越高。从HDFS读取基因表达谱矩阵，然后转化为RDD格式。每个worker节点运行一个迭代程序，并行地计算全部基因的加权信息能量WEHFS(Gk)。最终，通过key函数的reduce累加全部的能量值，将基因的ID作为key，信息量是key操作的目标。计算加权相关系数之前，driver生成一个三角矩阵，称为watch列表。master节点检查watch列表，验证两个条件：(1) 计算不同基因集{Ga,Gb}之间的加权相关性；(2) 每一对基因的加权相关性应当仅计算一次，即WCHFS(Ga,Gb)=WCHFS(Gb,Ga)。

算法4所示是计算距离的伪代码。在初始化阶段为watch列表的每个元素设置一个预定值，作为是否已经计算的标记。逐渐将watch列表的元素替换为计算的加权相关系数，每个worker节点并行地计算基因的加权相关系数。最终master节点在每次迭代结束更新watch列表，master节点在watch列表的约束下修改RDD的内容。在watch列表中没有相关系数记录的基因对保存于相同的RDD中，然后计算它们的加权相关性并保存于watch列表中。重复该迭代程序，最终使所有基因对均具有相关性记录。该程序具有可扩展性，能够处理任意规模的输入数据矩阵。

算法4计算距离的伪代码

输入：watch列表WLE。

1. for each (WLEi⊂WLE)

2. WLEi←0;

//初始化为缺省值

3. end for

4. while ((WLEi⊂WLE)==0)

5. shuffle_rdd()；

6. 计算WCHFS；

7. 更新WLEi；

8. 计算WρHFS；

9. 生成GPM；

10. 建立DRM

算法5是建立密度可达矩阵的伪代码。由近似矩阵生成密度可达矩阵，因为密度可达具有对称性，所以无须保存对称的可达性，密度可达也是三角矩阵形式。基因分布于各个worker节点，近似矩阵中基因Gi的第i列和第m+1-i行元素加入一个向量中，称为Vi，每个向量表示一个基因和其他所有基因的相似性，该向量被分配至各个worker节点。设计一个函数记录Vi中加权相关系数高于阈值((WρHFS)i,j>τ)的基因数量Gj。每个节点并行地调用计数函数，将计数值高于ξ(|Nτ(Gi)|>ξ)的基因标记为核心基因。

算法5建立密度可达矩阵

1. for each (Gi⊂RDD)

2.CntGi=0；

//初始化计数器

3. for each (Gj∈vector(Gi),i≠j)

4. if [(WρHFS)i,j>τ]

5.CntGi=CntGi+1；

6. end for

7. end for

8. for each (Gi⊂RDD)

9. if (CntGi>ξ)

10.Gi.coregene=TRUE；

//Gi标记为核心基因

11. end for

12. fore ach (Gi⊂RDD &&Gi.coregene == TRUE)

13. for each(Gj∈vector(Gi),i≠j)

14. if ((WρHFS)i,j>τ)

15.Gi⊂Gj；

//更新RGL(Gi),RGL(Gj)

16. end for

17. end for

18. for each (Gi⊂RDD)

19. for each (Gj∈RGL(Gi),i≠j)

20. list(Gi)⊂list(Gj)；

//更新RGL()

21. end for

22. end for

标记完所有的核心基因之后，将所有加权相关系高于阈值τ的基因标记为对Gi直接密度可达，即{Gi→Gj|(Gj)∈Nτ(Gi),Gi∈CG}。可能某个基因对于多个基因密度可达，所以采用一个可达基因列表(Reachable Genes List,RGL)记录对某个基因的密度可达基因。Gi被保存于Gj的可达基因列表中，Gj被保存于Gi的可达基因列表中。计算所有核心基因的直接密度可达之后，将直接密度可达泛化为密度可达。如果两个基因之间密度直达，那么列表内所有基因均为间接密度可达。

5.4 子聚类阶段

为每个基因Gi创建一个ID和数据结构，将序号i作为基因的ID，每个基因设置一个状态记录该基因是否被访问，并且设置一个状态记录该基因是否为核心基因。每个基因的列表RGL记录密度可达的邻居基因，根据密度可达矩阵DRM计算RGL。设置一个状态变量记录该基因是否为边缘基因，设置一个UID列表记录子类的UID值，将属于子类的基因添加到子类对应的UID列表中，如果基因的列表为空，说明该基因尚未被分配子类。

算法6是子聚类算法的伪代码。master节点将密度可达矩阵中的基因分配至各个worker节点，worker开始并行迭代子聚类程序。基因作为子聚类程序的输入，基因的子聚类结果作为输出。子聚类程序将核心基因作为初始化子类的中心基因Gi，对应的UIDi将添加到核心基因Gi的UID列表中。如果一个密度可达基因Gf是核心基因，则将UIDi分配到Gf和Gf的所有密度可达基因。worker节点nextUID()函数生成唯一的UID，该函数保证不同worker程序UID值不相同。

算法6子聚类算法

输入：RDD。

//Spark RDD数据库

输出：UID。

//基因的子类ID

1. for each (Gi⊂RDD&& CGstatus(Gi) == TRUE)

2. if (visiting_status(Gi) == UNVISITED)

//状态未访问

3. visiting_status(Gi) == VISITED;

//状态已访问

4. UID(i)←nextUID();

5. UIDlist(Gi) = UIDlist(Gi) + UID(i);

6. for eachGjin RGL_Gi

7. visiting_status(Gj) == VISITED;

8. UIDlist(Gk) = UIDlist(Gk) + UID(i);

9. if CGstatus(Gk) == TRUE

10.j=k；

11. end for

12. end if

13. end for

14. for each (Gi⊂ RDD&&((UIDlist(Gi)== NULL)‖(visiting_status(Gj) == FALSE)))

15. BGstatus(Gi) = TRUE;

16. end for

每个子线程首先处理尚未访问的核心基因Gj，为Gj分配新的UIDj和密度可达基因集，UIDj的基因访问状态变量修改为“访问”，最终访问完所有的基因。如果一个基因由两个不同核心基因密度可达，则其UID列表中会存在多个UID值。

在程序结束阶段将未被访问的基因标记为边缘基因BG。并且为每个子类指定一个骨架基因，骨架基因的决定方法为同一个UID列表中所有基因的HFE值，计算方法为：

(14)

式中：Gpro为骨架基因;hGPro是子类中所有基因的HFE;β是子类的基因数量。

5.5 融合阶段

将分布式处理获得的子类融合为总体的聚类。计算两个子类UIDi、UIDj之间的相同成员，如果满足以下任一条件：

(1) 子类UIDi和UIDj之间相同基因的数量大于ξ，即{Ga∈UIDi,Ga∈UIDj,i≠j,|Ga|>ξ}；

(2) 子类骨架基因之间的相似性大于τ，即{WρHFS(Gpro(UIDi),Gpro(UIDj))>τ,i≠j}。

那么将子类UIDi和UIDj合并为新子类UIDk。如果子类UIDi和UIDj合并为UIDk，那么UIDi和UIDj的类标签替换为UIDk，UIDk的基因数量等于UIDi和UIDj之和。

6 实 验

6.1 实验环境和参数设置

(1) 实验数据集和实验环境。在Hadoop YARN集群管理平台搭建独立的Apache Spark 2.0软件。单一的基因微阵列数据集对实验的工具和环境具有敏感性，为了提高实验结果的可靠性，减小噪声影响，采用多个微阵列数据集测试算法的性能。这些数据集组成了多条件、多实验下基因行为的犹豫模糊观察样本。

采用临床数据和人工合成数据从多个角度测试算法的各个性能：临床数据来自于不同的临床实验，设立相似的实验条件以评价结果的精度和效果；人工合成数据为大规模数据集，加入噪声数据测试算法的鲁棒性和可扩展性。第一个临床数据集[23]为肝脏组织的cDNA、核苷酸、表达谱数据，数据集包含430个基因芯片微阵列、cDNA微阵列和寡核苷酸，将该数据集简称为肝脏。第二个临床数据集[24]简称为POM，是体内裂殖酵母全局细胞循环控制的基因微阵列数据集，该数据集是多组实验的微阵列数据，并且是一个关于时间的函数。第三个数据集[25]简称为SPC，是一个大规模的数据集，测试本算法的可扩展性。

(2) RMA的参数设置。应用轮盘赌策略从种群中选择染色体，种群大小设为15，每对染色体应用两点交叉算子。染色体的第一个数量范围为[n/2,3n/4]，n是种群的特征数量。采用精英机制保留父种群和子种群的最优染色体，准确率的权重设为特征数量权重的4倍，容错度α=2。在RMA优化种群的过程中，保留种群中适应度高于动态阈值φ的i=3个最佳染色体。特征归简处理之后，收集β%个最佳的特征组成新的特征空间。根据实验结果分析，将参数β设为定值5，最大迭代次数为20次，ρ=94.5，w1=4，w2=1，q=0.3，step=0.5，初始种群的特征数量范围为[m/2, 3m/4]，m为染色体的特征数量。

(3) 聚类处理的性能指标。选择3个常用的聚类算法性能评价指标，分别为： 邓恩指数(Dunn Index,DI)、Davies-Bouldin指数(Davies-Bouldin Index,DBI)和Silhouette指数(Silhouette Index,SI)。

6.2 实验结果与分析

选择4种较新的聚类算法与本文算法做比较来综合评价本文算法的性能，分别为MBC[25]、HRSC[26]、MOOC[27]、EGWOM[28]。其中MBC是基于建模的聚类算法，HRSC是基于Hessian矩阵的聚类算法，MOOC是基于多目标优化的聚类算法，EGWOM则是基于灰狼优化算法和MapReduce的聚类算法。

(1) 聚类性能结果。图3、图4、图5分别为四个算法对于3个临床数据集的实验结果。DBI值越小表示聚类结果的簇内紧密，簇间分离大。观察实验结果可见，本文算法对于3个数据集的聚类准确率均优于其他4种算法，本文算法在聚类系统中采用犹豫模糊加权相关系数评估基因行为的相似性，根据基因的密度可达性将基因聚类，该设计对于高维小样本的基因微阵列数据实现了较好的效果。在特征归简处理中，采用文化基因算法对特征空间进行封装式的特征选择，实现了较好的优化效果，降低了基因的冗余度且排除了噪声基因。

图3 肝脏数据集的聚类性能结果

图4 POM数据集的聚类性能结果

图5 MOOC数据集的聚类性能结果

(2) 扩展性实验和计算效率。采用POM数据集作为人工数据集，测试算法的可扩展性和计算效率。将POM数据分别合成POM1、POM2、POM3、POM4四个数据集，POM1、POM2、POM3、POM4分别是将POM数据集复制1 000次、10 000次、100 000次和1 000 000次的数据集，结果如图6所示。可以看出，随着数据集规模10倍的扩展，SI指标并未呈现数倍的减低，数据规模增至1 000倍，SI指数大约降低0.1，DI指数大约降低0.15。结果证明了本文算法具有较好的可扩展性，对于大规模的数据集依然具有较好的聚类性能。

图6 扩展性实验的聚类性能结果

图7为不同规模数据集相应的处理时间。可以看出，随着数据集规模的指数级增长，处理时间也呈现出明显的升高。比较POM1和POM4，数据集规模增加了1 000倍，但是时间仅提高了约10倍，所以本文算法在计算效率上也具有较好的扩展性。

图7 扩展性实验的处理时间结果

(3) 与其他算法的处理效率比较。图8为5个聚类系统对于肝脏和SPC临床数据集的处理时间结果。可以看出，MBC和HRSC两个算法的处理时间均明显高于其他三个算法，主要原因是这两个算法是一种串行处理机制，虽然MBC算法通过多模型化简减小了特征空间和数据维度，但是依然保持较高的计算时间。HRSC在Hessian矩阵的处理过程中需要大量的计算，具有较高的计算成本。MOOC是一种多目标优化的聚类算法，该算法基于分布式多目标框架加快了计算速度，EGWOM则基于MapReduce框架实现了分布式处理，但是MapReduce具有以下三点不足：① 每次迭代作为独立任务重新处理，需要重新读写数据和初始化数据；② 每次迭代需要重新从分布式文件系统加载程序，消耗I/O资源和CPU资源；③ 前一次迭代必须全部结束并且数据全部写入分布式文件系统，才能开始下一次迭代,不仅具有较大的I/O开销，也导致了时间的延迟。本文算法基于Spark平台实现了分布式的处理过程，对于迭代处理程序实现了较快的速度。

图8 5个聚类系统的处理时间

7 结 语

为了支持海量高维小样本数据的分析和挖掘，设计了基于递归文化基因和Spark分布式计算的高维大数据聚类系统。该系统每次迭代作为独立任务重新处理，不需要重新读写数据和初始化数据；每次迭代直接从缓存系统加载程序，无须消耗额外的I/O资源和CPU资源。受益于递归文化基因算法和Spark分布式计算平台的诸多优点，本文算法实验获得了较好的聚类和聚类效果。

Spark平台将各个worker的数据缓存于内存中，无须消耗额外的I/O资源和CPU资源，但是增加了内存的负担，在海量高维小样本数据挖掘过程中产生大量的中间数据，导致不可忽略的内存负担，未来将关注于降低聚类系统的内存消耗。