基于复合模型的软组织变形模拟算法

谭时杰 郑津津 周洪军

1(中国科学技术大学精密机械与精密仪器系 安徽 合肥 230026) 2(国家同步辐射实验室 安徽 合肥 230029)

0 引 言

随着计算机技术的发展，虚拟现实技术成为了近几年来热门的研究方向。虚拟现实技术应用有许多方面，其中虚拟手术系统是虚拟现实技术的重要应用之一[1]。虚拟手术的对象是软组织，其系统需要具有实时性和精确性两个方面的要求。

目前，软组织模拟变形的研究一般采用有限单元模型或弹簧质点模型。例如：Tang等[2]提出一种基于约束的有限元变形模型来模拟虚拟手术中的软组织对象。Haouchine等[3]采用有限元模型模拟具有异质性的软组织对象，并在肝脏虚拟手术中进行应用。Duan等[4]提出了具有新的约束方法的弹簧质点模型来模拟软组织变形。Skornitzke等[5]将弹簧质点模型应用于二尖瓣修复手术的模拟上。就有限元模型和弹簧质点模型的特点来说，前者的特点是随着划分单元增多，模拟变形的精确度越高，但是计算处理时间变大，实时性变差。后者的特点是计算处理时间少，实时性好，但是精确度较低，使得变形模拟的真实程度大打折扣。基于位置的动力学模型是近些年来模拟变形的新方法。白隽瑄等[6]提出三维情形下的基于位置的动力学模型，并将其应用于脾脏和肝脏等软组织变形。Camara等[7]将基于位置的动力学模型应用于肾脏手术区域的模拟变形，并建立了肾脏手术的实时仿真平台。基于位置的动力学模型的特点是稳定性好，可以模拟出较好的视觉效果，但是精确度较低[8]。

本文提出一种结合了有限元模型和基于位置动力学模型的复合变形模型，包括复合网格的建立、复合网格中粗糙网格有限元模型的建立、复合网格中精细网格基于位置动力学中几何约束的选择、复合模型的变形计算处理流程。本文模型在确保实时性的情况下提升了变形的精确度，使得实时性和精确性达到了一个新的平衡。

1 复合变形模型

1.1 概 述

结合有限单元法模型和基于位置动力学模型的优点提出复合变形模型。在复合变形模型中，粗糙的四面体单元网格使用有限单元法计算网格变形，得到的变形约束着精细的三角形单元表面网格的一些控制点。而后，整个精细三角形表面网格的变形再通过基于位置动力学模型计算其他非控制点的变形，并做视觉渲染输出。

1.2 复合网格的建立

复合网格是由一个精细的三角形单元表面网格和一个与表面网格相匹配的粗糙的四面体单元网格组成。给定一个精细的三角形单元表面网格，生成与之相匹配的粗糙的四面体单元网格的过程如下：先用TetGen软件[9]生成精细的四面体单元网格作为基网格。再对基网格的顶点进行选择，得到的顶点集通过TetGen生成粗糙的四面体网格。基网格顶点的选择按最少顶点覆盖问题[10]解决。这些被选择的顶点作为体网格对表面网格的控制点，控制着表面网格的变形。图1以二维的方式展示了生成复合网格的过程。

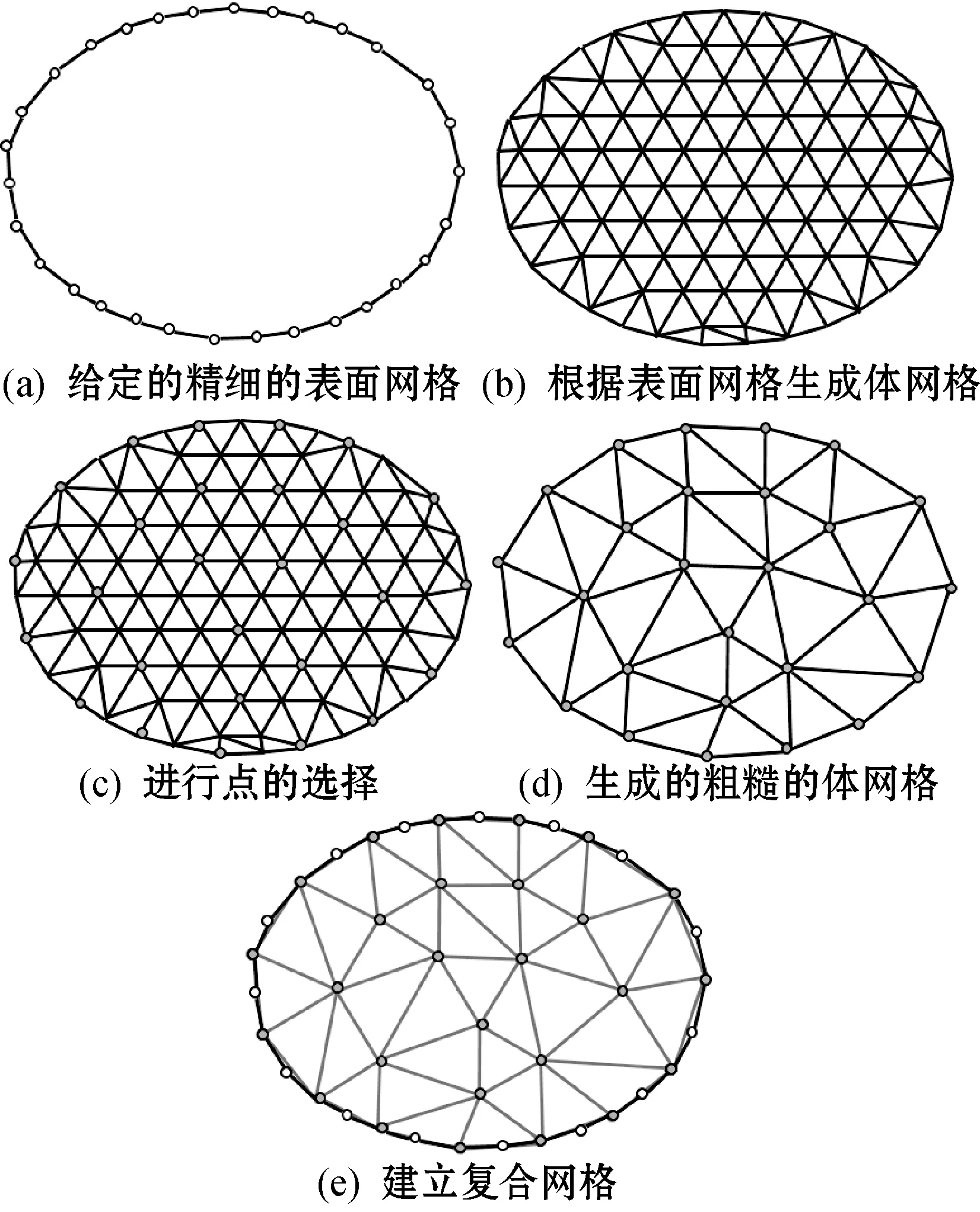
图1 复合网格建立过程

1.3 有限单元法

有限单元法是求解弹性理论中偏微分方程组最常用的方法之一。在有限单元法中，模拟区域Ω会被分解成一个有限单元的集合。模拟使用四面体单元网格对三维域进行离散。在这种空间离散化的基础上，采用有限元网格顶点位移插值的方法逼近连续位移场。具体来说，根据式(1)，利用单元顶点、单元形函数插值形成网格单元Ωe(e表示网格中各个单元内部的情形)的位移场函数。

uΩe(x)=Ne(x)ue

(1)

Ne(x)为单元形函数矩阵：

(2)

ue为网格单元节点的位移向量:

(3)

选择线性插值作为四面体离散化的形函数，它满足有限单元法的要求。

1) 满足单位分解：

(4)

2) 保证在相邻网格单元之间的连续性。

3) 满足克罗内克符号函数性质：

(5)

通过形函数，建立单元内应变于单元节点位移之间的关系：

εΩe(x)=Be(x)ue

(6)

式中：Be(x)是单元应变矩阵。

(7)

根据虚功原理，可得:

Keue=fe

(8)

式中：Ke为单元刚度矩阵；fe为单元载荷向量。

(9)

式中：D为弹性矩阵[11]。

(10)

根据单元间共享顶点的全局索引组合每个单元质量矩阵、单元刚度矩阵和单元载荷向量，得到一个针对整个网格的整体刚度矩阵和整体载荷向量，根据虚功原理可得：

Ku=f

(11)

要计算变形时，只需解式(11)获得u即可。

1.4 基于位置动力学模型

(1) 简介。基于位置动力学是一种通过控制点的位置来控制模型变形的算法。与基于物理的模型不同，该模型的迭代计算过程中，无须通过计算外力作用时的加速度，从而对加速度进行积分获取模型中各个点的位置变化。模拟时，首先对模型中各个点的位置、速度和质量初始化，模型中外力作用的顶点的位置发生变化，计算各个点的预测位置。预测位置再根据约束函数对模型中的每个点进行投影，以获得适合的位置。

每个约束函数为Cj(x1,x2,…,xi,…,xn)=0，其中：j为约束函数的序号，xi为第i个受约束点的位置；n为受该约束所影响的点的个数。对于当前点位置P，下一时刻位置为P+ΔP，约束函数可展开为：

C(P+ΔP)≈C(P)+▽PC(P)·ΔP=0

(12)

式中：ΔP为位置P的变化量;▽PC(P)为约束函数在P处的梯度。为了保证动量守恒和角动量守恒，ΔP与▽PC(P)的方向相同，从而有：

(13)

常用的几何约束有:两个点之间的拉力约束,两个三角形面片的弯曲约束,组成模型的每个三角形单元的面积应保持不变约束等。

(2) 拉力约束。拉力约束模拟了两个点之间的弹力，对于模型中的每条边，拉力约束函数为：

Cstretch(p1,p2)=|p1-p2|-l

(14)

式中：l为p1与p2之间的初始长度。图2为拉力约束的示意图。

图2 拉力约束示意图

p1、p2的梯度▽P1C、▽P2C分别为：

(15)

(16)

将式(15)和式(16)分别代入式(13)，有:

(17)

(18)

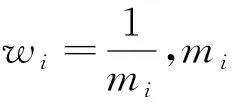
(3) 弯曲约束。弯曲约束为在外力的作用下两个三角形单元间的角度保持不变。图3为弯曲约束的示意图。

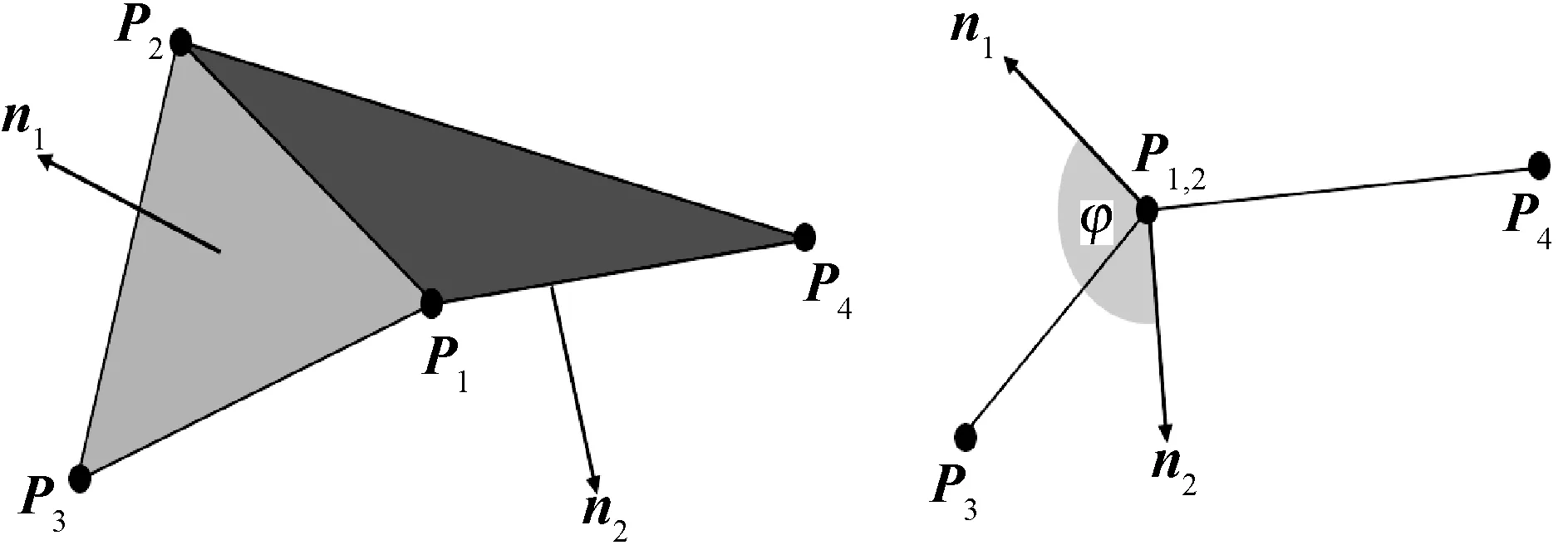
图3 弯曲约束示意图

对于模型中与每条边相邻的两个三角形单元(p1,p3,p2)和(p1,p2,p4)，弯曲约束为：

Cbend(p1,p2,p3,p4)=arccos(n1·n2)-φ=

(19)

式中：n1、n2分别为两个三角形单元(p1,p3,p2)和(p1,p2,p4)的法向量。

(20)

(21)

φ为(p1,p3,p2)和(p1,p2,p4)的初始二面角。根据式(19)、式(20)、式(21)，得梯度：

(22)

(23)

(24)

▽p1C=-▽p2C-▽p3C-▽p4C

(25)

将式(22)-式(25)代入式(13)，得：

(26)

其中:

q1=-q2-q3-q4

(27)

(28)

(29)

(30)

1.5 变形计算流程

1) 初始化：根据有限单元法计算四面体网格的整体刚度矩阵K，初始化三角形表面网格每个顶点的位置pi和速度vi，以及受力点的力f。

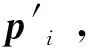
(31)

式中：f为外力。

3) 预测顶点位置:

(32)

4) 约束处理，分两部分处理。对于控制点:

(33)

(34)

(35)

6) 开始下个时间间隔，返回2)。

2 实 验

2.1 对比实验

实验平台配置为NVIDIA GeForce GT 520、Intel Core i3 CPU(3.60 GHz双核)和4 GB RAM内存。

复合网格使用的是一个立方体模型，该模型含有690个节点、1 380个三角形单元精细的表面模型网格，根据1.2节，生成复合网格。复合网格中生成的粗糙的四面体网格含有153个节点和411个单元。

基于位置的动力学模型使用的是前文复合网格模型中精细的表面网格。有限元模型使用的是前文提到的复合模型中的精细的表面网格，用TetGen生成精细的四面体网格。该精细四面体网格含有3 028个节点和17 044个单元。有限元模型使用精细体网格而不采用粗糙体网格的原因是在对比实验中有限元模型的变形实验结果将作为评价精确度的标准，对于有限元模型来说，划分单元越多，变形结果的精确度越高。

实验中，复合变形模型使用复合网格，有限元模型选择精细四面体网格，基于位置动力学模型使用精细表面网格进行实验。在立方体顶部表面的中心点施加垂直立方体底面向上的拉力和向下的1 N压力。记录三个模型的上表面变形区域的变形量和变形时间。图4为对比实验变形结果展示。

图4 对比实验变形结果

通过计算复合模型和有限元模型的顶部表面变形量的相关系数来评价本文中复合模型变形的计算精确性。其值越接近1，则复合模型与有限元模型顶部表面变形量之间的相关度越高。表明复合模型变形的精确度较基于位置动力学模型有很大提升。结果如表1所示。

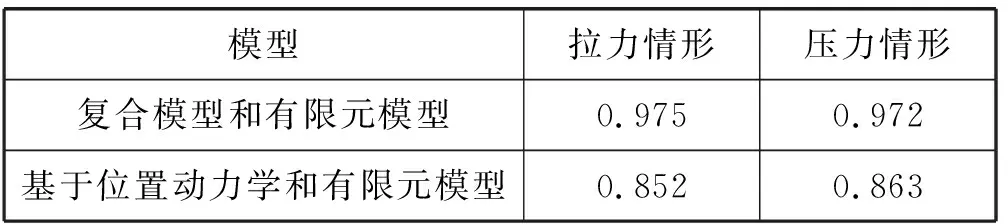
表1 复合模型和有限元模型、基于位置动力学和有限元模型的顶部表面变形量的相关系数

通过对比复合模型、基于位置动力学模型和有限元模型的变形计算处理时间来评价本文复合模型的时间效率。处理时间越短时间效率越高。结果如表2所示。

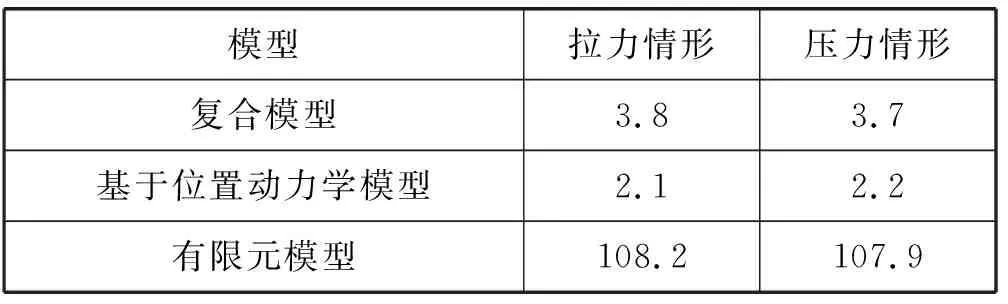
表2 复合模型、基于位置动力学模型和有限元模型的平均每帧处理时间 ms

实验结果表明，复合模型相对于传统的基于位置动力学模型在变形量计算的精确性上具有优势，复合模型相对于有限元模型在时间效率上具有极大优势。复合模型在变形计算的精确性和时间效率之间取得了一个较好的平衡。

2.2 复合模型变形实例

选取肝脏模型来展示变形实例，该肝脏复合模型的精细表面模型含有1 316个节点和2 608个三角形单元，粗糙体模型含有181个节点和596个四面体单元。图5展示了肝脏模型及其提拉与下压变形效果。两种变形情况下的处理时间如表3所示。实例显示了复合模型对实体模型也有很好的展示效果。

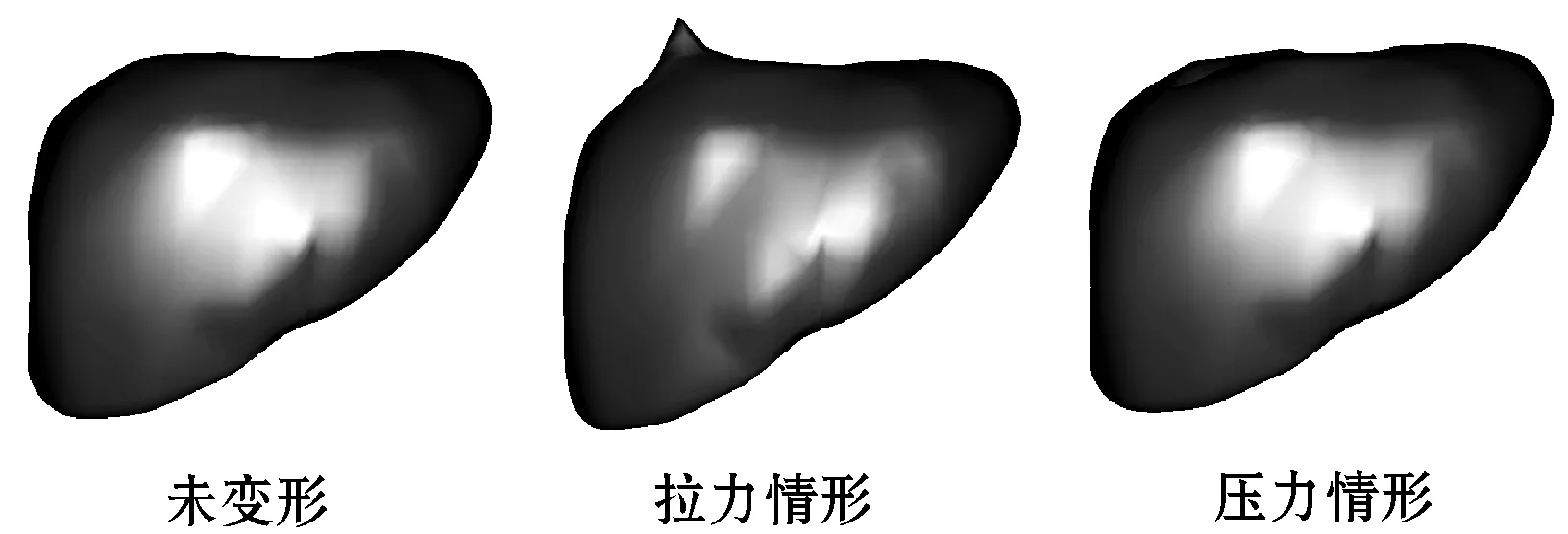
图5 肝脏模型及其提拉与下压变形效果

表3 变形实例中两种变形情况的变形计算处理时间 ms

3 结 语

本文提出复合模型来模拟虚拟手术中软组织的变形。在复合模型中，粗糙的四面体单元网格采用有限元模型，精细的三角形单元表面网格采用基于位置的动力学模型，粗糙的体网格通过控制点约束着精细的表面网格变形。复合模型按照变形计算流程实现变形模拟。在实验中，复合模型与传统的有限元模型和基于位置的动力学模型进行拉力情况和压力情况的模拟变形对比。通过收集变形面的变形量数据，计算复合模型的数据与有限元模型的数据的相关系数以及基于位置的动力学模型的数据与有限元模型的数据的相关系数，表明复合模型变形模拟的精确性较基于位置动力学模型有较大优势。在变形计算处理时间方面，复合模型也可以保持实时性。综合两方面考虑，复合模型在变形计算的精确性和处理时间之间取得了一个较好的平衡。最后，本文展示了复合模型的变形实例，将复合模型运用到了肝脏模型上，结果表明复合模型应用于实体模型时也有很好的展示效果。