基于DDPG算法的海上无人救援技术研究
郑 帅 贾宝柱,2* 张昆阳 张 程
1(大连海事大学轮机工程学院 辽宁 大连 116026) 2(广东海洋大学海运学院 广东 湛江 524088)
0 引 言
海上应急救援往往受海况恶劣、时间紧迫等因素限制,救援成功的关键在于遇险目标位置的确定和如何快速靠近遇险目标。海上遇险目标会随着风、浪、流的作用而发生漂移,由于各种海洋漂浮物的受风面积与水下面积不尽相同,即使在同一风场与流场中,落水物的漂移轨迹也不相同[1]。相关研究表明,落水人员在20 ℃海水中最长存活时间为16小时20分钟,而在0 ℃海水中最长存活时间仅为12 分钟[2],即使遇险人员能够利用救生艇、筏等延长存活时间,但也受到淡水、食物等补给限制。
目前,海上救援主要依靠人工的经验驾驶船舶应对海上多变的复杂环境追踪遇险目标,但是海上环境恶劣,使执行救援任务时有较高的安全风险。随着船舶无人驾驶技术的发展,海上无人救援研究受到了广泛重视[3]。
针对遇险目标位置漂移问题,多数研究采用了预测遇险目标漂移轨迹的办法。旷芳芳等[4]结合风场和流场的数值模拟,给出了落水人员和救生筏的风致漂移系数,用于预测落水人员以及救生筏的实时位置。刘同木等[5]基于MMG模型研究了风、浪、流的作用下船舶的漂移数学模型。Gao等[6]通过蒙特卡洛方法在疑似马航370航班遇难海域对其残骸的漂移轨迹进行预测。漂移模型预测方法的不足在于无法找到一个通用的预测模型对不同漂移目标的位置进行预测。同时,已有的多数研究工作仅仅关注预测方法准确度,却没有考虑遇险目标的快速追踪及靠近的问题。根据SOLAS公约规定,每艘救生艇、筏要求至少配备一台搜救雷达应答器(Search and Rescue Radar Transponder,SART),用来近距离确定遇难船舶、救生艇、救生筏,以及幸存者位置[7]。因此,实际救援场景中更可靠的是根据SART所提供的实时目标位置信号开展营救。
当遇险目标的位置已知,就要考虑如何快速靠近遇险目标的问题。Park等[8]基于视觉的估计和制导方法,控制无人机追踪移动目标。李静等[9]提出交通道路网络环境下的局部搜索树移动目标追踪算法。Woo等[10]设计了强化学习控制器,使无人船具备了自主路径跟踪的能力。本文尝试将DDPG深度强化学习算法应用于海上无人救援,结合SART所提供遇险目标位置信号,设计了基于机器人操作系统[11](Robot Operating System,ROS)仿真实验平台。在Gazebo物理仿真器中模拟水文环境以及船舶的运动特性,使搜救无人船在感知环境信息的同时,通过对不同漂移轨迹的落水物进行追踪实验,训练其追踪漂移遇险目标的能力。
1 目标跟踪算法设计
1.1 船舶运动模型
一般情况下,船舶运动研究通常只考虑三个自由度的运动,通过 Gazebo插件实现双体船操纵的非线性运动学模型,船舶操纵公式[12]如下:
Mv+C(v)v+D(v)v=τ+τenv
(1)
η=J(η)v
(2)
式中:M是惯性矩阵;C(v)是科里奥利矩阵;D(v)是阻尼矩阵;τ是推进系统产生的力和力矩向量;τenv是通过Gazebo插件模拟的风、浪、流干扰力;向量η描述了惯性参考系北(N)、东(E)中的位置和绕Z轴的转首角度φ;η= [x,y,φ]T和向量v包含船体固定坐标系中的船体的纵向速度u、横向速度v和转首角速度r,即v=[u,v,r]T。船体坐标系到惯性坐标系的坐标转换关系为:
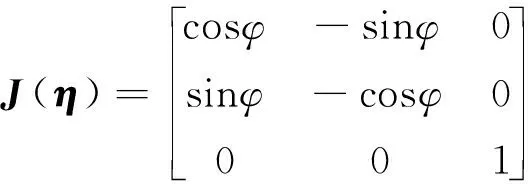
(3)
1.2 状态空间设计
为追踪到不同的遇险目标,使算法具有一定的泛化性,搜救船的环境模型需要考虑遇险目标的位置,得到遇险目标与搜救船的相对位置关系,这种关系包括二者之间的距离d以及船舶的首向与二者连线方向的夹角φ,环境模型状态如图1所示,定义状态s为:
s=[d,φ]T
(4)
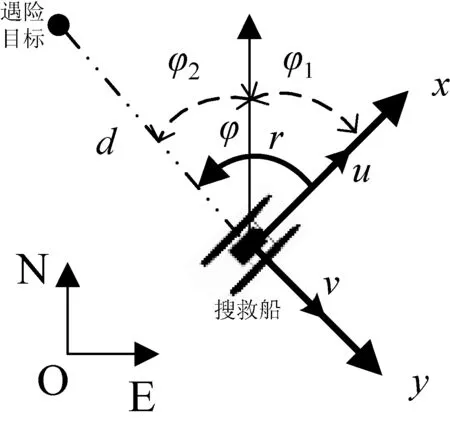
图1 状态示意图
当搜救船捕获到SART反射的雷达信号,在雷达屏幕上形成12个一连串的光点,这种显示方式用来区别于其他雷达回波信号,其中最靠近雷达中心点的光点便是遇险目标的位置(xt,yt)。另外,通过船舶运动模型计算我们船的位置信息(xv,yv),可以计算出二者之间的距离d。
(5)
φ=φ1-φ2(-180<φ,φ1,φ2≤180);φ1通过模型计算得出,其为首向角,即船首方向与正北方向的夹角;φ2为遇险目标和搜救船的相对方位,即二者连线与正北方向的夹角。
φ2=arctan((xt-xv)/(yt-yv))
(6)
1.3 动作空间设计
对环境状态的改变依赖于智能体通过驱动装置使船舶发生运动,双体船通过电机指令驱动两个螺旋桨产生差速推力来驱动搜救船移动。动作空间由一组电机指令组成,指令发布时间间隔为1 s,定义动作空间a为:
a={[m+n,m-n]T|m∈[-0.5,0.5],n∈[-0.5,0.5]}
(7)
式中:m表示双体船的双桨转速值;n表示左右螺旋桨差动值。参考文献[12]中的系柱实验得出的单浆推力与电机指令之间映射关系,得到搜救船的驱动力τ,根据船舶操纵模型以及坐标转换公式可以计算出当前指令执行后船舶的位置姿态。
1.4 奖励函数设计
由于救援任务具有时间相关性,所以奖励函数的设计需要考虑时间与距离因素。奖励函数用rt表示。
(8)
式中:t表示时间环境反馈奖励值为(2-0.01×t),设计成为时间相关函数,目的是引导搜救船用尽量短的时间完成追踪任务;dt表示当前采样获得的搜救船与遇险目标的距离;dt-1表示上一次采样的距离。将上一次的距离与当前的距离做差,如果当前距离比上次距离短,差值为正,反之为负,φ角同理,这种设计目的是引导搜救船朝着遇险目标的方向逐渐靠近,获得相对较高的奖励值。
2 DDPG算法
环境观测值与动作值由深度确定性策略梯度下降(Deep Deterministic Policy Gradient,DDPG)[13]算法进行处理。DDPG算法需要两套神经网络,分别为主网络与目标网络。每套网络都由一个Actor(演员)网络与一个Critic(评论家)网络构成。两套网络的网络结构完全相同,只是参数不同。
该算法是在梯度下降法的基础上,对Actor-Critic算法进行改进,将输出动作选择概率转变为输出确定动作值的强化学习算法,这个确定性的zs915121动作是随机策略梯度的极限值。Actor-Critic算法框架由两个网络构成,包含了以求解值函数为核心的Critic网络,还有以策略为核心的Actor网络。其中Actor网络的输入为状态矩阵,输出确定的动作值at,而Critic网络的输入为动作值at与状态值st,输出动作的Q值,Q值对当前回合的一系列动作策略做出评价,因此,训练该网络的过程是判断动作策略优劣的学习过程,通过训练,得出Q值最大的一系列动作策略。
每一步采集的样本(st,at,r,st+1)输入到主网络中训练,采样过程如图2所示,同时开辟一个记忆库来存储采样的结果,目标网络则随机抽取记忆库中的数据作为输入,记忆库的数据不断更新,切断了样本数据间的相关性。主网络的参数通过回合更新的方式,若干回合后,将主网络参数赋值给目标网络,进行目标网络的参数更新。
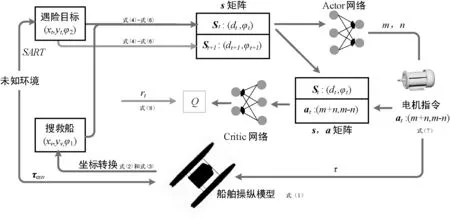
图2 样本采集过程
算法具体流程如下:
(1) 构建Actor网络与Critic网络,主网络参数分别为θμ、θQ,并进行随机初始化。Critic网络得到的Q值为Q(s,a|θQ),Actor网络得到状态到动作的映射μ(s|θμ)。
(2) 通过网络参数θμ、θQ来初始化所要求解的目标网络的参数θμ′、θQ′,同时开辟一个记忆库存储空间。
(3) 初始化状态s1,通过主网络加上高斯扰动Nt,从动作库中选择一个动作at进行探索:
at=u(s|θμ)+Nt
(9)
(4) 执行该动作,得到相应的奖励rt和下一个状态st+1,并且形成元组(st,at,rt,st+1),作为一条采样值存到记忆库存储空间中。
(5) 通过当前网络Q(s,a|θQ)进行估计,同时从记忆库中选取一小批元组数据,通过Bellman方程对Q值进行估计,估计结果表示为:
q(ai)=ri+γQ(si+1,μ(st+1|θμ′)|θQ′)
(10)
式中:γ表示折扣率,反映未来估计的奖励对当前决策的影响程度,如果γ=0,则不考虑未来任何价值;如果γ=1,则未来的价值不会随时间衰减。
将计算出的两个值做差,得到损失函数TD_error。然后使用梯度下降法对Critic网络的参数进行更新。
(6) 主要采取策略梯度的方式进行Actor网络的更新,即:
▽θμμ(s|θμ)|si
(11)
在得到策略梯度后,通过最大化期望奖励的方式对总奖励进行梯度上升更新参数。
(7) 若干回合后,将主网络的参数赋值给目标网络,对目标网络参数更新。
(12)
算法结构如图3所示。
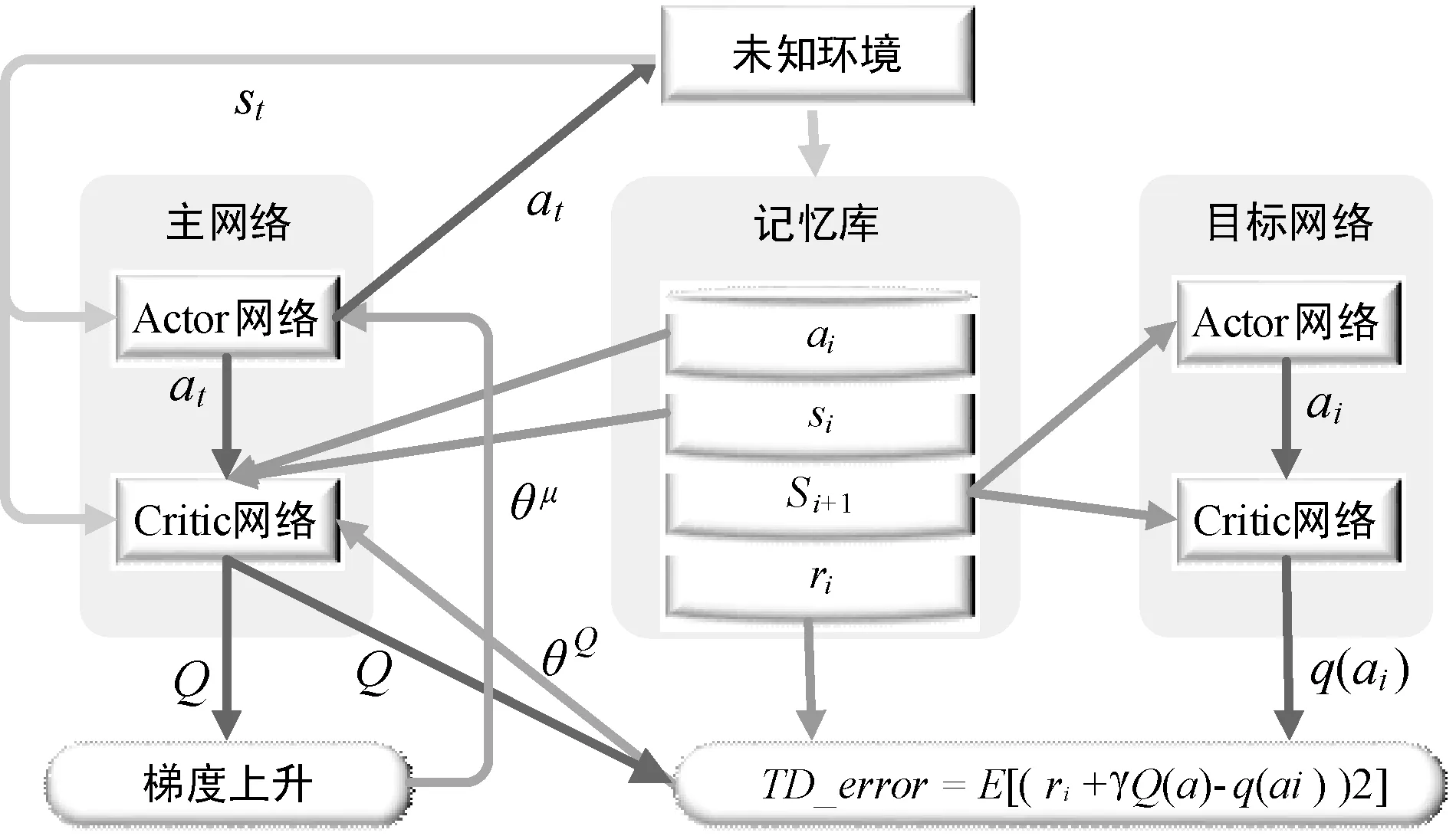
图3 DDPG算法结构图
使用TensorFlow搭建Actor网络和Critic网络,Actor网络的输入为状态矩阵,网络结构有两个隐藏层,每个隐藏层的节点分别为400、300,输出动作矩阵。将状态矩阵输入到Critic网络中,该网络第二层有400个节点,第三层有300个节点。动作矩阵也输入到Critic网络,第二层有300个神经元节点,并将状态空间矩阵输入的网络的第三层神经元与动作矩阵输入的网络的第二层神经元节点合并进行线性变换,输入到第四层网络神经元节点上,该层共有300个神经元节点,最后输出动作的Q值。网络的所有神经元节点之间的连接方式均为全连接方式,网络结构图如图4所示。
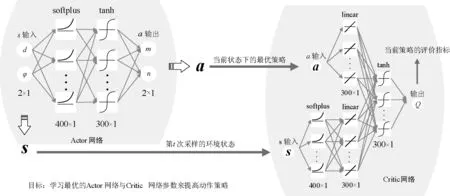
图4 Actor-Critic网络结构图
3 实 验
3.1 实验平台
实验设计基于ROS,在Gazebo物理仿真器中创建三维实验环境与智能体,模拟海上救援场景,设定环境场景边界为50×50的范围,初始状态下搜救船位于(0,0)的位置,并在环境扰动的干扰下运动,遇险目标位于(20,10)的位置。当搜救船与遇险目标的距离小于5时,视为满足成功救援的条件。Actor网络的学习率为0.000 1,Critic网络的学习率为0.001,折扣因子为0.99。每次实验的总回合数为1 000,每个回合最多采集200个样本数据,由于搜救船执行电机指令需要一定的时间,设置样本采集的时间间隔为1 s。记忆库的容积为10 000,批数据的容量为64。奖励函数的系数为ξ,ζ均为1,目标网络更新参数κ为0.01。
3.2 实验设计及结果分析
3.2.1直线轨迹目标追踪
从图5中可以看出,实验初期(前200回合),由于探索的概率比较大,这一阶段搜救船在探索环境,采集环境样本数据,很难准确追踪到遇险目标,平均Q值Qa也较低,只有少数成功的情况,Q值较高。从图6中可以看出,这一阶段用时都相对较长。实验中期(200~500回合),随着样本数量的累积,逐渐建立起了奖励函数与动作策略之间的联系,搜救船从探索环境知识逐渐转为利用环境知识,逐渐可以追踪到遇险目标,算法快速收敛,但是会走一些弯路。随着训练的不断深入,搜救船会不断地调整自己的运动趋势,以最短的时间靠近遇险目标,最终Qa稳定在10,平均时长ta稳定在70 s。从Q值以及时间的变化趋势来看,算法符合救援过程中时间紧迫性的要求。
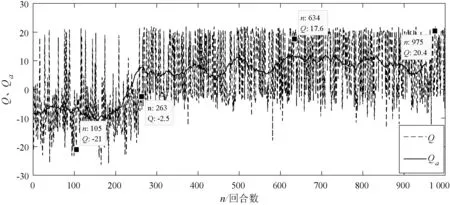
图5 Q值以及平均Q值(Qa)变化曲线一
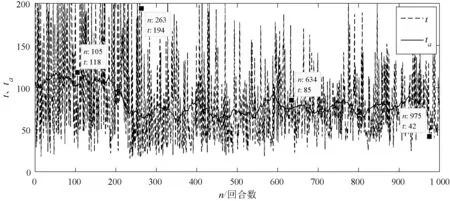
图6 回合时长以及平均时长(ta)变化曲线一
从三个阶段中选取第105回合、第263回合、第634回合,以及第975回合训练过程进行分析,如图7所示,分别对应(a)、(b)、(c)、(d)的四幅轨迹图,其中虚线轨迹为搜救船的运动轨迹,实线轨迹为遇险目标的漂移轨迹。可以看出只有第105回合训练失败,结合图5可以看出,奖励值最低,其他三个回合均成功追踪到了遇险目标。随着训练深入,第263、第634、第975回合搜救船的轨迹渐短,Q值越高,结合图6可以看出所用的时间也越来越短。
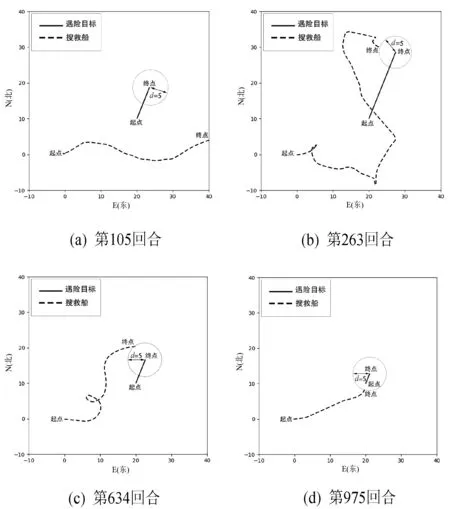
图7 搜救船及遇险目标运动轨迹一
在Gazebo仿真环境中可以观察到以上四个回合结束时搜救船与遇险目标的相对位置如图8所示,其中黑色的圆点为回合结束时遇险目标的位置。

图8 回合结束时Gazebo场景一
由图9可以直观地看出上述四个回合的样本的实时奖励值变化趋势。第105回合(曲线a)奖励值多数情况下是负数,表明搜救船一直在远离遇险目标,因此Q值比较低,为-21。而第975回合(曲线d)则每一个动作都是在靠近遇险目标,因此奖励值很高,高达20.4。其他两个回合(曲线b和曲线c)均有正有负,表明追踪过程有远离的情况,这两个过程中的动作策略不是最优的策略。从图7的轨迹图中也可以看出这一点,证明奖励函数的设计可以引导搜救船快速追踪到救援目标,是有效的。
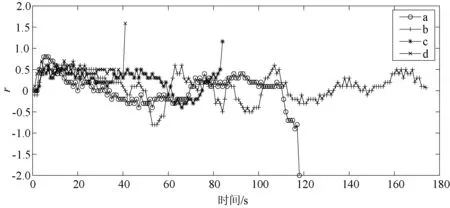
图9 单个回合奖励值随时间的变化曲线对比一
3.2.2不规则轨迹目标追踪
由于不同落水物体在海上的轨迹不同,为证明算法的有效性,补充了不规则轨迹落水物的追踪实验。从图10中可以看出与直线轨迹追踪实验结果相似,随着环境状态样本采样数量的增加,搜救船由探索环境转变为利用环境知识,从第200回合开始算法逐渐收敛;平均Q值(Qa)逐渐增加,最终稳定在15左右。从图11中可以看出完成任务所需的平均时间(ta)逐渐减少,用时较少的回合可达28 s。由此可见,尽管不同的遇险目标漂移的轨迹不同,甚至轨迹变得不规则,搜救船仍然可以通过DDPG算法达到快速追踪到遇险目标的目的,算法仍能够收敛。
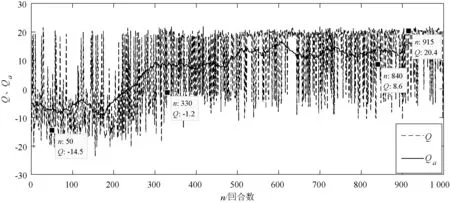
图10 Q值以及平均Q值(Qa)变化曲线二
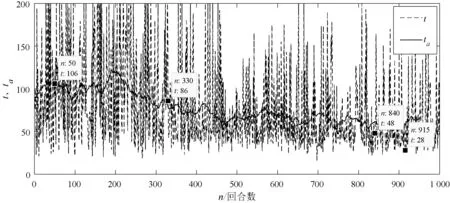
图11 回合时长以及平均时长(ta)变化曲线二
选择第50、第330、第840、第915回合,运动轨迹分别如图12(a)、(b)、(c)、(d)所示,同样虚线轨迹为搜救船的运动轨迹,实线轨迹为遇险目标的漂移轨迹。第50回合中搜救船没有能够追踪到遇险目标,而第330、第840、第915回合均完成了对遇险目标的追踪任务,并且第915回合的轨迹是最短的,用时最少,Q值也是最高的。
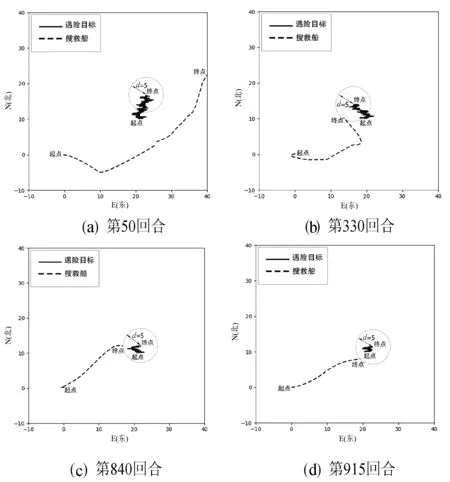
图12 搜救船及遇险目标运动轨迹二
上述四个回合在回合结束时, Gazebo中显示的相对位置如图13所示,黑点表示回合结束时遇险目标的位置。

图13 回合结束时Gazebo场景二
通过对以上四个回合中的每一次采样获得的奖励值变化进行分析,如图14所示。从曲线e可以看出,算法未建立起奖励函数与动作策略之间的关系,与遇险目标的距离时远时近,曲线在0附近波动。而曲线g和曲线h表示在这两个回合中每次采样的奖励值大多位于0.5以上,表明搜救船与遇险目标正在快速靠近,再一次说明奖励函数的设计是有效的。
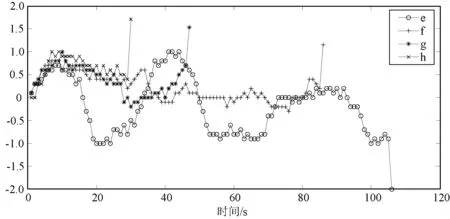
图14 单个回合奖励值随时间的变化曲线对比二
4 结 语
在海上无人救援过程中,针对遇险目标漂移问题,本文提出一种基于DDPG算法的目标追踪方法,本文所做的研究工作及相应结论可为实船实验提供参考。主要结论如下:
(1) 分析了强化学习算法应用于海上无人救援情景的技术难点,在未知遇险目标的漂移模型情况下,当获取遇险目标与自身相对位置时,算法可以使搜救船自主做出恰当的操纵决策,以较短的时间靠近遇险目标,通过直线漂移轨迹的遇险目标追踪实验和不规则漂移轨迹的遇险目标追踪仿真实验得以验证。
(2) 将强化学习算法与海上实际救援情况相结合,设计状态、动作空间、相应的奖励函数,奖励函数的设计考虑了时间因素与距离因素。经过仿真实验验证,奖励函数能够引导无人搜救船快速地追踪到遇险目标,并且具有一定的泛化性,符合海上搜救时间紧迫性的要求以及目标追踪距离逐渐缩短的要求。

