基于Wi-Fi和自适应蒙特卡洛的移动机器人定位方法的研究

刘 鹏 刘 凯 周 愉

(成都信息工程大学 四川 成都 610225)

0 引 言

定位是移动机器人导航技术中的一个关键环节。在一个简单的导航任务中，移动机器人需要获知自己在当前环境中的准确位置，才能顺利地由初始位置A移动到目标位置B。在已知自己准确位置信息的前提下，服务型机器人可以轻松地完成从厨房拿一杯咖啡送至客厅任务。Pinheiro等[1]认为机器人在自身位置已知的情况下也可以很好地帮助人类完成日常家庭的清洁工作。除此以外，自主定位与导航技术还广泛地应用于自动运输车辆的集装箱码头、自动驾驶汽车等方面。在自动驾驶领域，文献[2]提出全球定位系统(GPS)可以为车辆提供必要的位置信息，但由于其定位误差过大，不适用于定位精度要求较高的场所。

1 相关工作

移动机器人的定位是利用当前位姿信息、先验地图信息和传感器输入信息来预判机器人下一时刻位姿的过程[3]。从概率的角度来看，机器人的定位问题就是状态估计的问题。由于基于概率的方法普遍具有很好的鲁棒性，因此很多概率估计方法适用于移动机器人的位置估计。经典卡尔曼滤波(KF)和扩展卡尔曼滤波(EKF)方法虽可以有效地解决移动机器人的姿态跟踪问题，但其要求系统必须是线性系统且满足高斯分布，所以卡尔曼滤波方法(KF)在实际应用中会产生很多问题[4]。为了解决上述问题，使用了粒子滤波算法(PF)的蒙特卡洛定位法(MCL)在移动机器人定位问题上的效果显著[5-6]。该方法利用一组离散加权粒子对估计状态后验概率增加的过程进行模拟，通过状态预测的步骤完成对粒子过滤，权重更新和重新采样。蒙特卡洛方法的主要特点是可以有效地应用于非线性和非高斯系统，但这种方法无法解决当移动机器人因姿态突然改变产生的机器人“绑架”问题，且其难以从定位失败中恢复过来[7-8]。当其定位环境规模较大时，蒙特卡洛方法还存在粒子的退化风险。在粒子退化过程中，绝大多数颗粒的权重变得非常小，只有一个或几个颗粒的权重发生了相对较大迭代。针对上述问题，Li等[9]提出了自适应蒙特卡洛定位方法,不仅给予了移动机器人从“绑架”中恢复过来的能力，还使用了KLD采样方法调整粒子的数量和解决粒子退化的问题。受上述文献启发，本文提出了一种基于Wi-Fi和自适应蒙特卡洛的移动机器人混合定位方法，解决了传统自适应蒙特卡洛(AMCL)方法存在的初始位姿定位效果差、粒子收敛速度慢、定位所需移动距离远等问题。实验结果表明，通过引入Wi-Fi三角定位算法改进自适应蒙特卡洛(AMCL)定位方法，在明显缩短定位时间的同时，很大限度上提高了移动机器人初始化定位精度。

2 Wi-Fi定位原理及信号衰减模型

2.1 Wi-Fi定位原理

文献[10-12]最早提出了利用Wi-Fi进行移动机器人的定位，其具体方法是利用Wi-Fi接收信号强度和方向采用三角定位技术估计当前位置。无线局域网技术用于距离接入点20～100 m的数据计算机网络的无线交换。它是基于IEEE 802.11标准在2.4或5 GHz频带上完成超过1 Gbit的吞吐量。本文的Wi-Fi定位系统是由三个相同规格的路由器和一个移动机器人构成，其三个路由器的分布情况如图1所示。

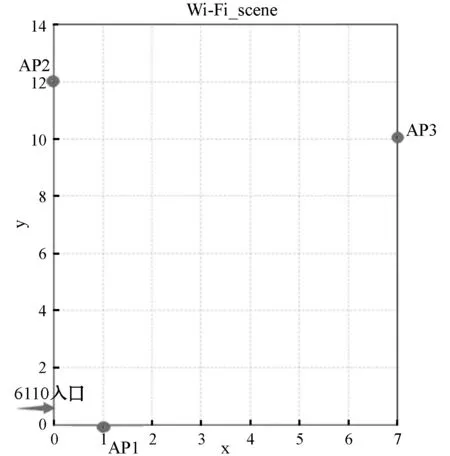
图1 路由器分布

Wi-Fi初始定位法首先是通过接收多个AP接收信号强度值，之后根据接收信号强度和一定的信号衰减模型来估计距参考点的距离。本文将通过实际信号衰减模型计算出实际位置已知的AP与未知节点距离之间的关系，利用此距离推算未知节点的绝对位置信息。该方法产生的误差主要是由环境对信号的影响造成的。在传播过程中，无线信号会受到反射、折射和多径效应的干扰，使得现有的基本信号衰减模型可能不适用于当前的测量环境，从而导致出现很大的定位误差。因此需要在实验环境中实际测量记录每个信号发射节点的实际发射功率，然后记录稳定环境下信号传播损耗的实际情况，并根据损耗建立衰减模型[13]。最后，基于接收点的RSSI的实际消耗，使用损失模型计算未知节点与参考节点间的相对距离，通过三角定位法来确定待估计节点的实际位置坐标。Wi-Fi初始位置定位流程如图2所示。

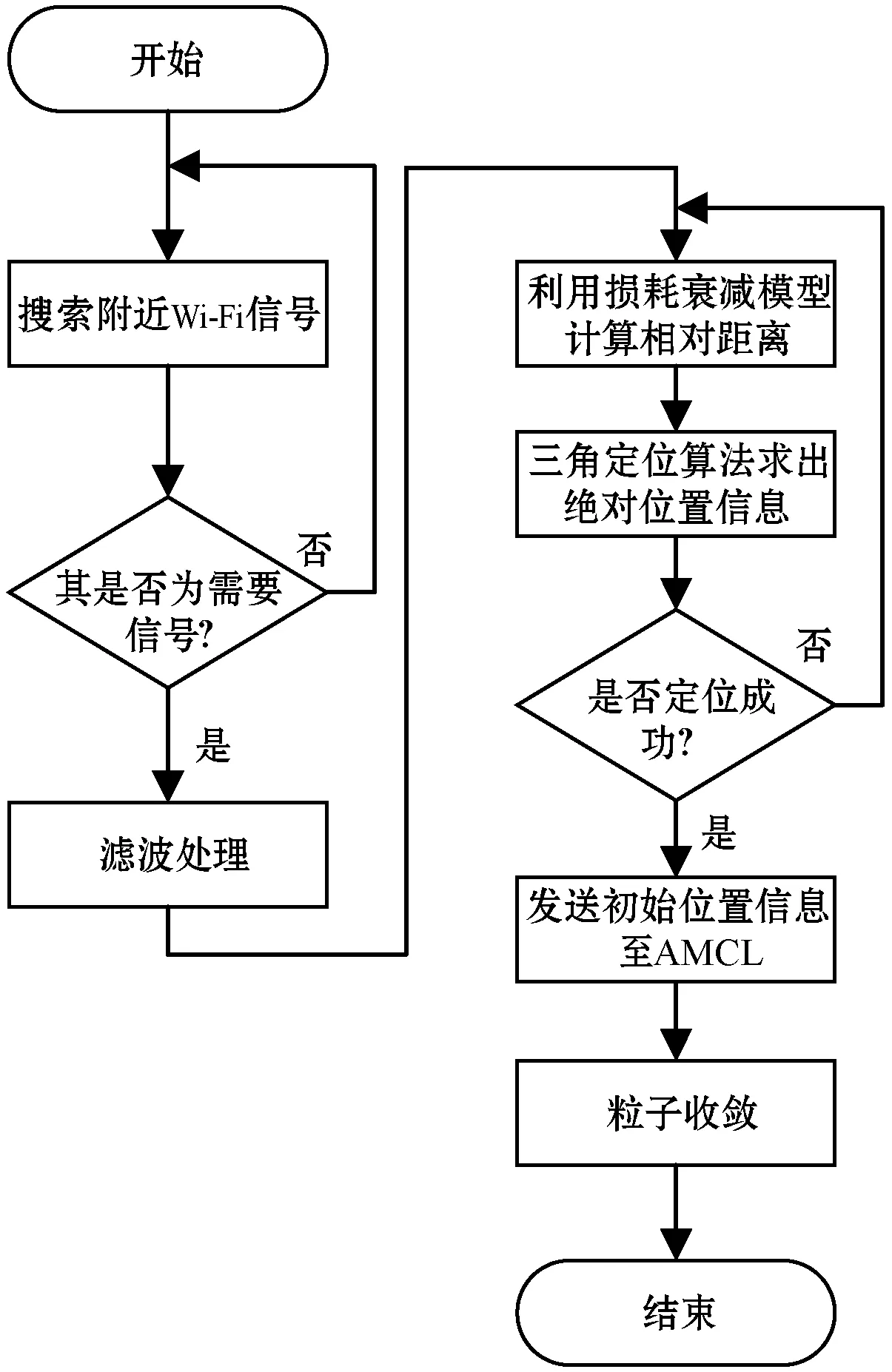
图2 Wi-Fi初始定位流程

首先移动机器人开始搜索附近多个的AP的接收信号强度值(RSSI)，在对无效值信息进行剔除后将其发送至信号衰减损耗模型进行计算，估计信号实际传播距离。然后选取三个最近的距离值作为三角定位算法的输入，得到初始位置的坐标信息，将其作为自适应蒙特卡洛算法的初始位姿输入。经过一段时间的粒子收敛得到机器人最终位姿信息。

2.2 信号衰减模型

无线信号本质上是一种电磁波，它通常在大气之中传播。由于大气环境中颗粒物质分布不均，导致其在传播时容易发生折射、散射和多径现象，致使其能量被大气吸收，到达信号强度发生衰减[14-15]。一般来说，信号强度的大小是由特定的信号值表示，其单位为dB或dBm。在理想情况下，Wi-Fi信号在真空中传播速度最快，损耗最小，但在现实生活中，真空的传播环境是不存在的。所以在信号传播过程中，其不可避免地会造成能量损失。Wi-Fi信号传播损耗模型主要分为自由空间损耗模型、对数距离损耗模型和衰减因子损耗模型三种。自由空间损耗模型又称理论覆盖模型，是无线电波传播最简单的模型，在给定信号频率时只和距离有关。但由于其不能在复杂的室内环境下准确地反映环境特征，故不适用于本文实验环境。而衰减因子损耗模型一般适用于信号由室外向室内传输(遭受建筑物阻挡)，信号强度发生严重衰减的情况。由于本实验环境存在较多诸如桌椅和大型设备等障碍物，因此选用复杂条件下环境特征效果较为明显的对数距离损耗模型。其信号传输公式为：

(1)

式中：L[dB](d)是机器人与AP之间距离为d时的路径损耗；d0是参考距离(通常参考距离设为1米)；L(d0)是机器人与AP之间距离为d0时的路径损耗；Xσ为覆盖因子，服从平均值为0、标准差在4～10之间的高斯分布，Xσ值越大，代表测距误差越大；n为路径损耗因子，即单位距离内的信号功率衰减率，该值一般为1～6，具体取值视室内环境条件而定。距信源距离为d时接收到的无线信号强度为：

RSSI(d)=Pa-L(d)

(2)

式中：RSSI(d)表示当前时刻的信号强度；Pa是AP发送时的功率。当d=d0时，由式(2)得：

RSSI(d0)=Pa-L(d0)

(3)

将上述公式代入式(1)可得：

(4)

(5)

式中：Xσ是均值为0的一个正随机变量。故可得到距离公式：

(6)

式中：RSSI(d0)为单位距离处的信号强度。

下面实验将在实验环境中的信号采集点上进行信号强度采样，每个信号采集点进行100次实验采样，最后计算100个样本的平均值作为采样点处的信号强度值。具体的采样点分布情况如图3所示。

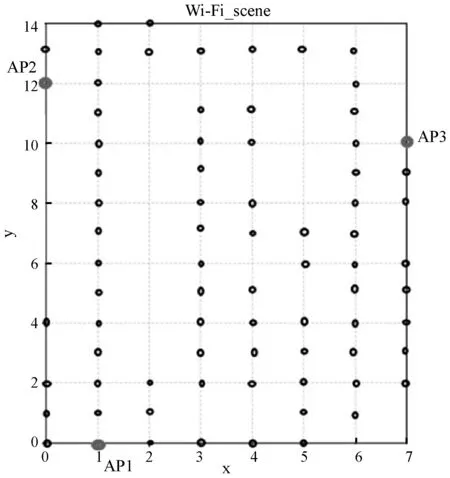
图3 Wi-Fi采样点分布(未能采样处均有大型障碍物)

由上述采样结果可得实验环境中AP1、AP2、AP3的信号强度分布分别如图4、图5、图6所示。

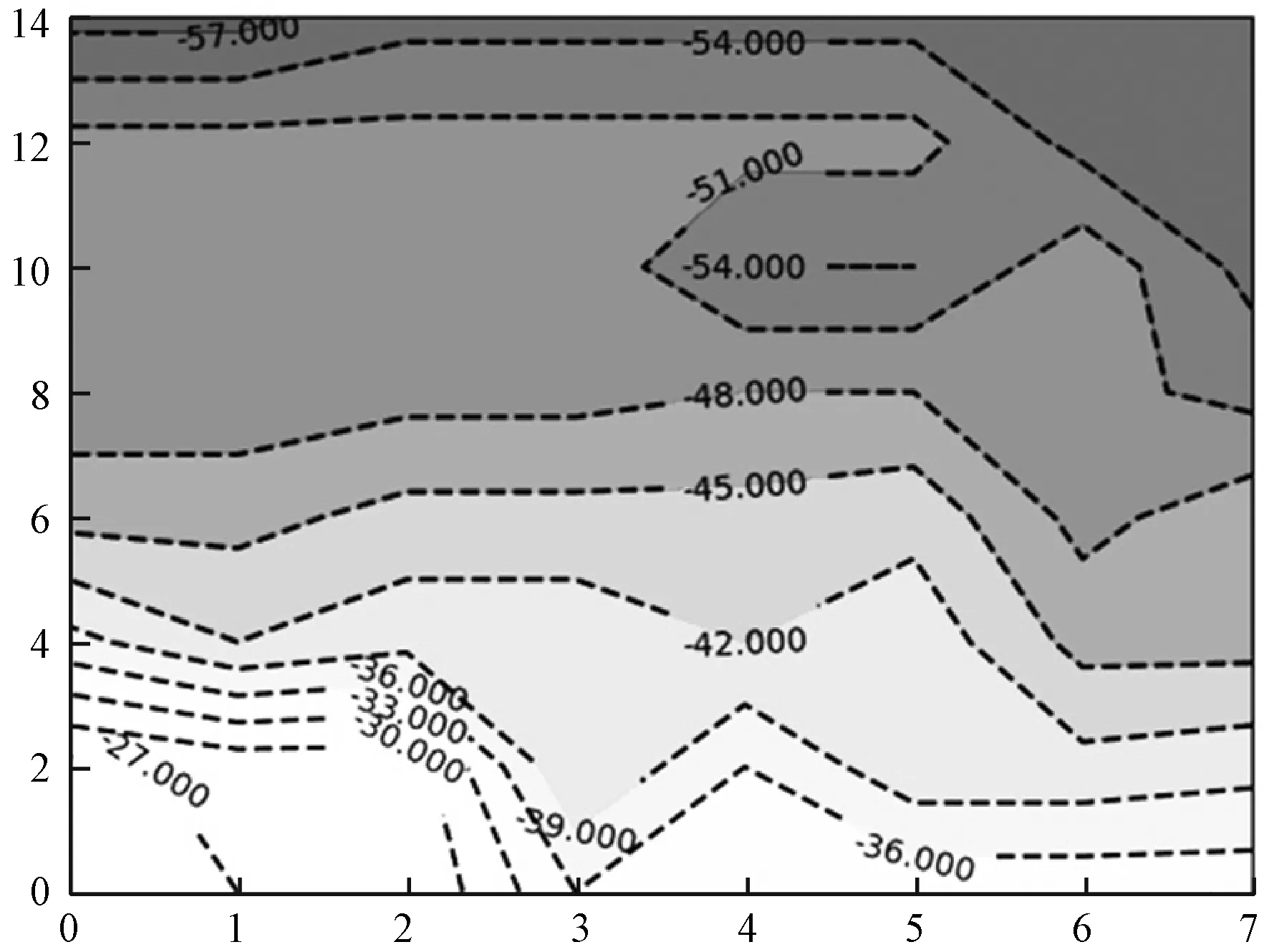
图4 AP1信号强度分布

图5 AP2信号强度分布

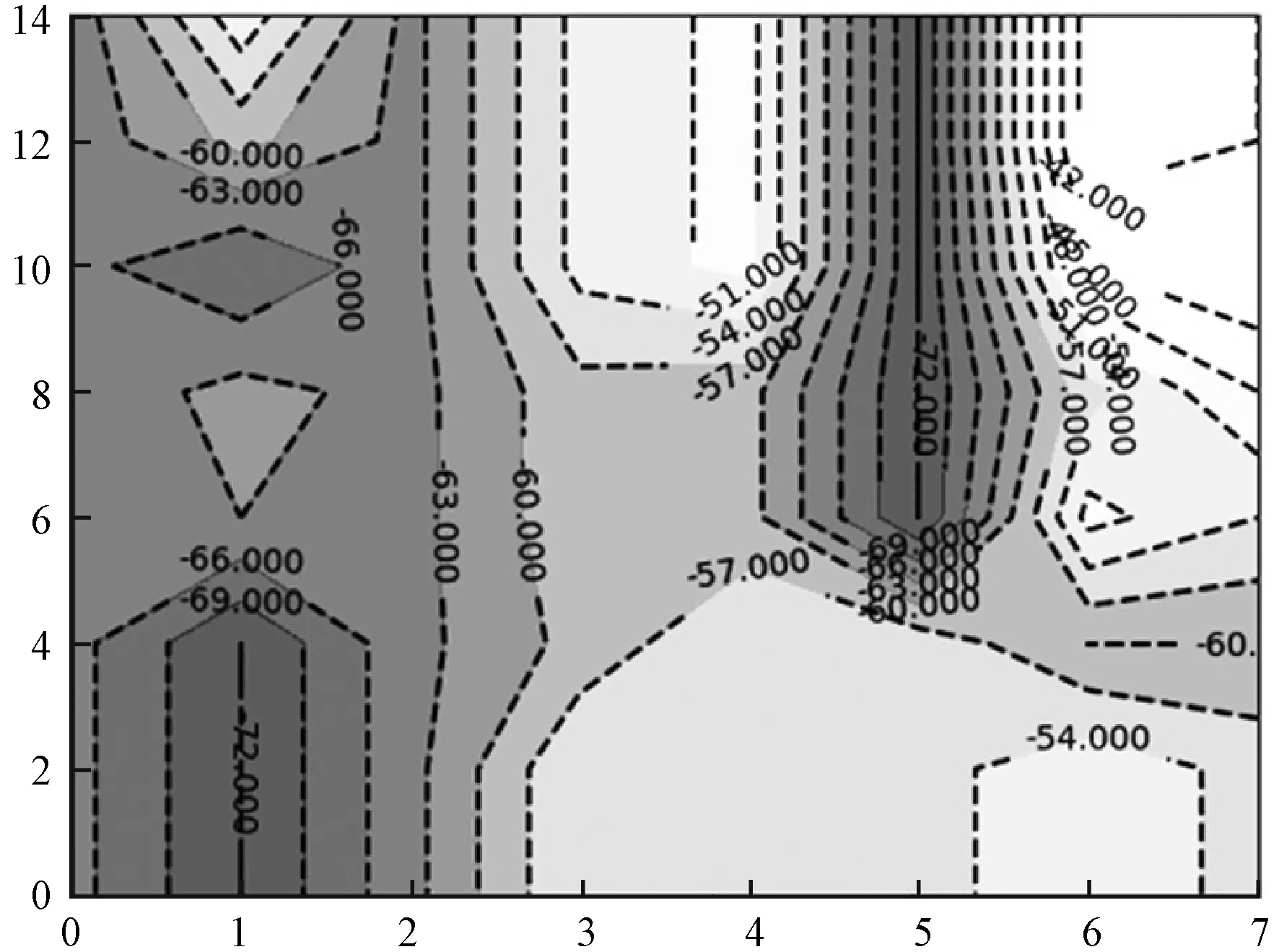
图6 AP3信号强度分布

3 Wi-Fi三角定位算法

3.1 自适应蒙特卡洛算法

自适应蒙特卡洛定位算法是MCL(Monte Carlo Localization)算法的一种改进。蒙特卡洛定位算法适用于局部定位和地图较小的全局定位，已成为机器人定位领域的主流算法。蒙特卡洛定位算法的原理较为简单，首先将随机粒子均匀地散布在需要定位的局部或全局地图上，每个粒子的位姿即代表机器人此刻可能的一种位置姿态。当机器人向前或向后移动一段距离时，所有粒子都按照自己当前的位置和姿态在地图上向前或向后移动一段距离。此后，算法将与机器人自身的运动不一致的粒子除去，保留剩余正确的粒子，经过一段时间的粒子收敛后，剩余的粒子位置即代表了机器人当前所处位置。在某种程度上，粒子只能在单个位置附近“存活”，如果这个位置不正确，则算法就无法恢复。所以MCL算法仍然存在无法从机器人绑架或全局定位失败中恢复的问题。实际上，当粒子数量很小时，任何随机算法都可能会意外地丢失在正确位置附近的所有粒子。而AMCL算法有效地解决了该问题，AMCL算法在机器人遭遇绑架时注入新的随机粒子。AMCL定位是指在地图已知的情况下，机器人通过使用传感器的观测结果来确定其位置。由于机器人的运动过程具有不可预测性，AMCL方法通过产生许多随机粒子来估计机器人在地图上的位姿状态，每个粒子都包含对未来可能状态的完整描述。当机器人观测到周围环境特征时，它会丢弃与此观测结果不一致的粒子，并生成更多与观测结果一致的粒子。随着移动机器人的不断运动，基本上所有粒子都收敛至机器人实际所在的位置，以此达到定位的目的。移动机器人系统的运动状态模型表示为：

xt=ft(xt-1,ut-1)

(7)

式中：xt代表系统t时刻的运动状态；xt-1代表系统上一时刻的运动状态；ut-1表示系统的控制噪声。机器人系统的观测模型可表示为：

zt=ht(xt,vt)

(8)

式中：zt表示当前时刻的观测状态信息；vt表示系统观测噪声。

(9)

根据移动机器人的系统动力学，可得其拟议分布为：

(10)

位姿xt的后验可靠性估计为：

(11)

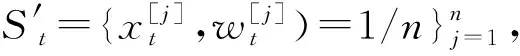
(12)

由AMCL算法中提出的拟议式分布原理可以看出，当其系统缺少及时的观测信息zt时，该方法容易使采样粒子集的观测似然函数分布过于尖锐或为零，最终导致机器人定位失败，如图7所示，使用AMCL算法进行初始化定位效果较差。

(a)

可以看出，微小颗粒表示随机粒子，图中箭头表示机器人运动方向，图7(a)的圆点表示机器人实际所在位置，图7(b)的圆点表示粒子最终收敛的位置。图7展示了机器人初始化位姿的收敛过程，在该过程中，机器人初始化定位结果在五个位置反复跳跃，引起粒子聚集错误，致使定位收敛时间长，定位性能不高，鲁棒性较差。

3.2 三角定位算法

Wi-Fi定位算法基本上分为两类。一类是非基于Wi-Fi信号强度，例如TOA(到达时间)、TDOA(到达时间差)；另一类是基于Wi-Fi信号强度的RSSI方法。三角测量定位算法是基于接收信号强度的最为典型的算法之一。三角测量定位过程主要分为两个阶段，即测量阶段和定位阶段。测量阶段是将接收点的信号强度代入2.2节所述的对数衰减模型中，计算出其与参考目标点的相对距离。本节主要介绍定位阶段。通过三角形算法分别计算待测点与三个AP的实际距离，将位置已知的三个AP作为圆心，将测量点与AP之间的距离作半径画圆，得到三个圆的交点，如图8所示。

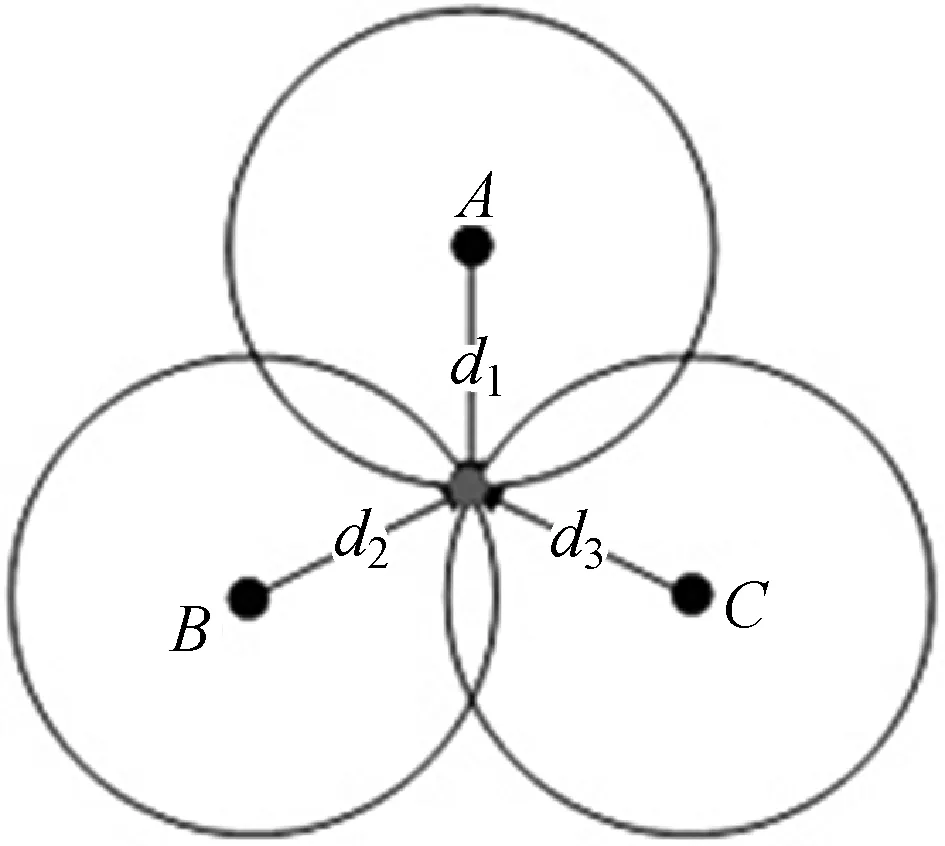
图8 三角定位算法原理

假设A、B、C是三个参考节点，其坐标分别为(x1,y1)、(x2,y2)、(x3,y3)，中心灰点是未知坐标(x,y)。从灰点到A、B、C三点的距离分别为d1、d2、d3。此距离可由2.2节的对数路径损耗模型计算获得。根据欧氏距离的计算公式可得方程组如下：

(13)

其未知机器人的坐标可以通过矩阵方程求解：

(14)

但实际应用中，由于误差等原因，三个圆一般不会交于一点，而会交于一个区域，如图9所示。当三个圆相交于一个区域时，通常认为未确定的位置在该区域内，即图9中三点之间的区域。一般来说，对于三圆的公共区域，求得两两相交圆的割线，最终三条割线的交点即为待估计目标位置。

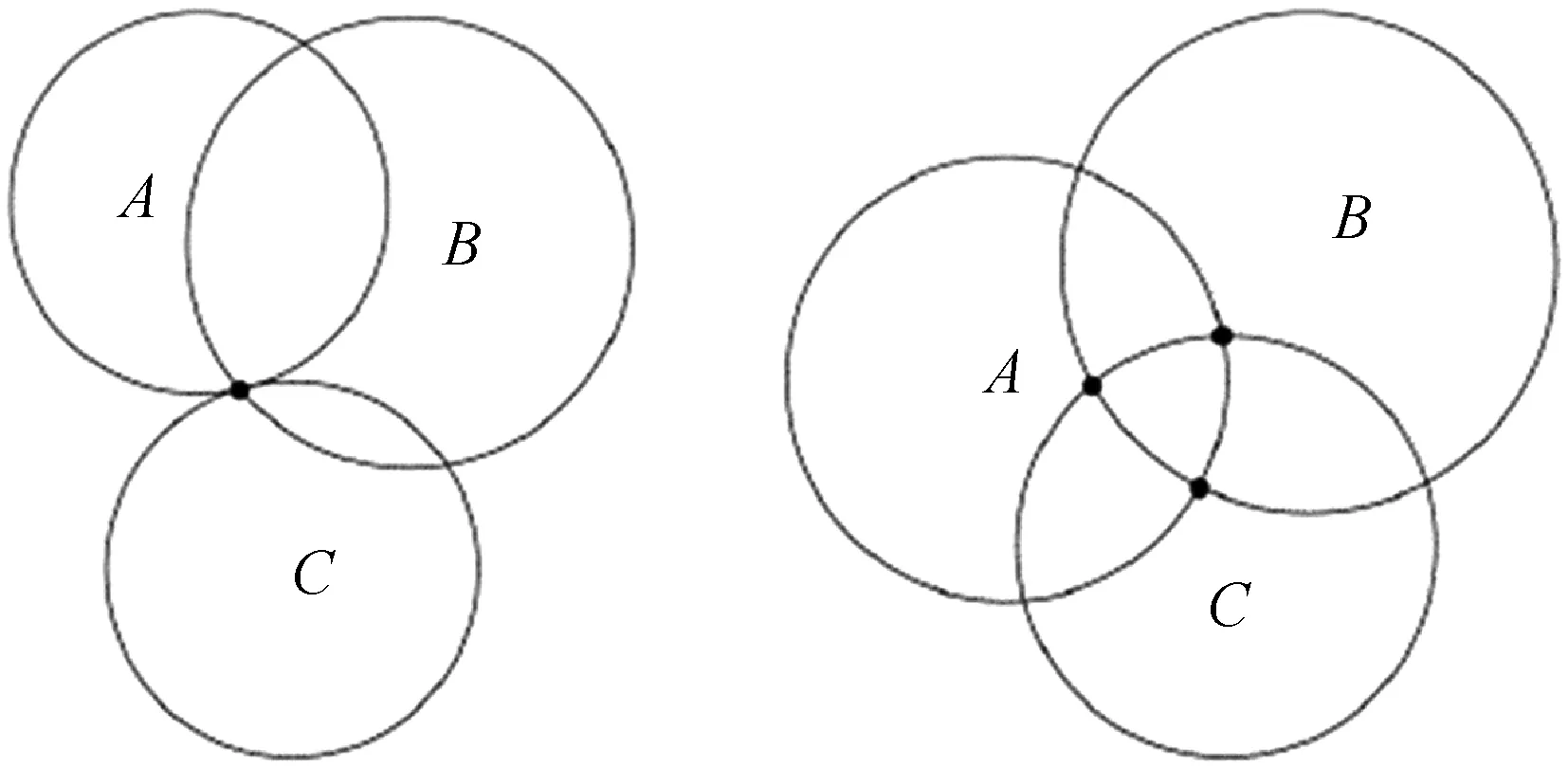
图9 三圆交于一个区域的两种情况

3.3 自适应蒙特卡洛和Wi-Fi混合定位算法

本文为了使用Wi-Fi三角定位法辅助自适应蒙特卡洛改善其初始位置定位效果，将Wi-Fi定位位置结果输入Initial_pose，作为AMCL定位的初始位姿。机器人通过感知其所在环境特征，不断更新其粒子，直到可以准确地反映其位置。对于每个粒子，机器人通过计算得知当前粒子的状态与传感器观测到的环境状态之间的相似概率，并按照此概率成比例地为粒子分配权重w[i]t。然后再从上一时刻概率较大的粒子群中随机抽取M个新粒子，抽取个数与其概率成比例，与传感器观测状态一致的粒子被保留下来，不一致的粒子被除去，逐步使粒子收敛至与机器人更相似的状态。机器人利用三角测量算法的将初始化定位结果将发送至AMCL的初始节点，然后AMCL执行至完成收敛。与传统方法相比，该方法在提高了初始位姿定位准确度的情况下，还大大降低了随机粒子的收敛速度。

由拟议式分布的原理可见，拟议的分布越接近提议分布函数，粒子滤波器的滤波效果就越好。 一些非系统因素(如驱动轮滑动、不均匀地面等)可能会使里程计传感器的运动模型产生很大的偏差，导致机器人定位失败。为了获得更为理想的提议分布，本文通过EKF融合里程计和IMU的传感器数据，结合运动模型和观测模型生成更为合理拟议式分布。该方法可以通过IMU校正里程计误差，所得提议分布更加接近后验概率机器人姿态状态的分布，可以有效提高AMCL的定位精度。本文提出的基于Wi-Fi三角定位算法和AMCL定位方法的过程如图10所示。

图10 混合算法的定位过程

4 实 验

为了验证本文方法的有效性，下面将通过对比实验来说明Wi-Fi三角定位算法是怎样辅助AMCL算法实现精确定位的。本文的仿真验证过程是在Ubuntu16.04系统的ROS机器人仿真平台上进行的，使用的是CPU为2.6 GHz、内存容量为8 GB的华硕笔记本电脑，在仿真结果可视化方面采用了ROS中的可视化工具Rviz。

本文在上述相同条件下设置两种不同的全局定位方法，一种方法是使用传统的自适应蒙特卡洛进行全局定位，随机粒子分散在整个地图上然后逐渐收敛在一个位姿上；另一种方法将使用Wi-Fi位置估计结果作为AMCL初始位姿状态，使随机粒子分散在一个较小的区域内。

4.1 粒子收敛速度的比较

在使用传统的AMCL对机器人进行定位时，其初始化随机粒子遍布于整个地图上，随着机器人的不断移动最终收敛于机器人位置周围。本文实验通过控制机器人原地旋转，直至状态粒子收敛于一点，其结果如图11所示。其中：图11(a)的圆点代表机器人位置，微小颗粒色代表AMCL随机粒子所在的位置和方向；图11(b)的箭头表示机器人运动方向，圆点代表随机粒子最终收敛的区域位置。

(a)

可以看出，传统AMCL初始化定位过程所需的时间为29.58 s。在相同环境条件下使用Wi-Fi位置估计辅助AMCL进行定位时的结果如图12所示。

(a)

对比可知，粒子初始化定位比之前更加集中且不会遍布整个地图空间。融合方法的初始化定位时间仅为6.75 s，可见该方法较传统方法具有更快的收敛速度，使其初始定位时间明显缩短。

4.2 定位所需移动距离的比较

在AMCL定位过程中，随着机器人不断移动，随机粒子逐渐收敛于机器人周围。此实验通过控制机器人直线移动一定距离，使随机粒子收敛于一点，对比其达到收敛状态时的移动距离，其结果如图13、图14所示。

图13 传统AMCL定位所需的移动距离

图14 Wi-Fi-AMCL定位所需的移动距离

可以看出，Wi-Fi-AMCL方法需从初始状态移动8.83 m后可以得到自身准确位置，而传统AMCL方法在相同条件下则需要19.95 m移动距离。上述实验结果表明，本文方法有效地加快了粒子的收敛速度，缩短机器人初始化定位的计算时间。

4.3 定位误差的比较

在使用传统AMCL算法时，当其系统缺少及时的观测信息zt时，很容易使采样粒子集的观测似然函数分布过于尖锐或为零，导致其定位误差较大。实验通过控制机器人到达指定目标位置，分别测试20组初始定位结果数据，其结果如图15、图16所示。

图15 传统AMCL定位误差范围

图16 Wi-Fi-AMCL定位误差范围

机器人周围的圆形范围表示20组初始定位测试结果的误差范围。图15中传统AMCL全局初始化定位的误差半径为1.47 m；图16的Wi-Fi-AMCL初始定位结果则具有较小的误差范围，误差半径为0.83 m。以上实验结果表明基于Wi-Fi-AMCL融合方法不仅可以有效加快粒子的收敛速度，缩短机器人的定位时间，而且在一定程度上提高了定位精度，改善了定位效果。

5 结 语

本文通过对实验环境中Wi-Fi信号的分布进行测试，利用Wi-Fi信号强度的三角定位法，在ROS平台上实现了Wi-Fi-AMCL室内初始定位系统。本文共进行了三个实验，用于测试Wi-Fi-AMCL方法的初始定位效果。结果表明，在使用Wi-Fi-AMCL方法进行初始化定位时，其收敛速度比传统方法更快，所需定位时间更短。基于Wi-Fi-AMCL融合方法不仅可以有效加快粒子的收敛速度，缩短机器人的定位时间，而且在一定程度上提高了定位精度，改善了定位效果。总而言之，Wi-Fi定位方法的引入，在提高自适应蒙特卡洛定位方法初始位置的定位精度过程中有着显著的效果。