基于神经网络的电子战人力资源规划分析

刘歌声，赵禄达，沈从勇

(国防科技大学，安徽 合肥 230037)

0 引 言

电子战越来越成为现代局部战争中的决定性、制胜性力量，在近期的美伊、美俄中东局部冲突中都发挥出左右战争结果的巨大作用。而电子战在实际作战过程中需要大量电子战人员的参与，包括电子战军官、士官、技师以及文职人员等。

随着现代智能化战争的迅速发展，第4代、第5代电子战装备陆续问世，各国电子战能力的大幅提高，电子战人员的需求量也出现了大幅的增长。这样，电子战人力资源规划问题就显得格外重要。目前，国内外对电子战的研究主要集中于政策、体制编制方面[1-2]，而对电子战人力资源规划的研究还不广泛，按照现代战争的发展趋势对电子战人员需求变化趋势进行研究还很少。

本文研究基于神经网络理论的电子战人力资源规划方法，通过建立兵力需求规划模型、神经网络预测模型和电子战k级人员补充模型，为电子战人力资源规划提供了一种有效的思路和方法。

1 电子战人力资源规划思路分析

军事人员的人力资源规划主要是军事人员系统状态分析。系统状态随时间的演变主要与内外的人员流动有关。系统内部流动有晋升、降级、平调等；内部与外部之间的流动有招募(入伍、调入、提干等)、退休、转业、复原、调出和其他减员等[3]。

本文研究电子战人员规划的思路和方法主要是分为3个过程，即首先按照总体兵力，根据国内外形势变化，确定电子战兵力比例，得到电子战兵力，其次通过若干间隔时间计算的电子战兵力数据代入神经网络模型，推测下一阶段的电子战兵力数量，最后通过推测的电子战兵力数量对电子战人员补充系统进行人员数量信息的确定。通过以上步骤，将电子战人力资源规划从顶层到底层进行连贯分析，可以为决策者提供很好的决策辅助。电子战人力资源规划过程如图1所示。

2 电子战人力资源规划模型构建

2.1 电子战兵力需求规划模型

一般而言，兵力规划对于某个国家的军队来说属于战略层级的任务。但电子战兵力的规划有灵活、多变的特点，随着战场和阶段任务的实时变化会产生很多无法预测的情况，所以电子战兵力规划一般需要结合战略、战役层级以及国家发展需求等实际情况共同考虑[4]。

首先，基于国家军事战略、国内外政治、经济、外交等情况和重大突发性事件影响(战争突然爆发、发生大型自然灾害以及重大卫生防疫事件等)因素，保证部队正常运转的条件下，兵力规划目标为打赢随时可能发生的局部冲突和战争。其次，综合考虑以上因素后，根据可能对手的电子战兵力数量，依据专家经验以及敌我兵力数量、状态比等因素，确定电子战兵力需求比n。最后，再根据国家部队总员额得出各个时期电子战兵力的数量。那么，在模型1中总共需要确定以上4个具体数值ni(i=1,2,3,4)。

2.2 神经网络预测模型

神经网络理论是根据现代人类神经系统的研究慢慢发展而来的，是一种通过模拟人类神经活动和神经信息传递方式对数据信息进行处理、练习，产生一定的处理信息规律，对未知信息进行进一步处理、预测和分类。经过50多年的发展，神经网络理论被各行各业认同和广泛运用，可分为前馈网络(多层感知机)和反馈网络(Hopfield网络)。其中，比较著名的是BP神经网络(NN)、RBFNN、GRNN、PNN、支持向量机等。本文主要以BP神经网络和RBF神经网络2种算法对电子战人员进行数据处理和预测。

2.2.1 BP神经网络预测模型

BP人工神经网络模型一般有3个基本要素：输入层(Input)、隐含层(Hidden)以及输出层(Output)。数据需要在网络中进行不断的迭代和训练，从而找到一套合适的连接权值，对数据可以进行预测和分类。

BP神经网络作为反馈型神经网络的代表，具有很好的系统鲁棒性。网络连接示意图如图2所示。

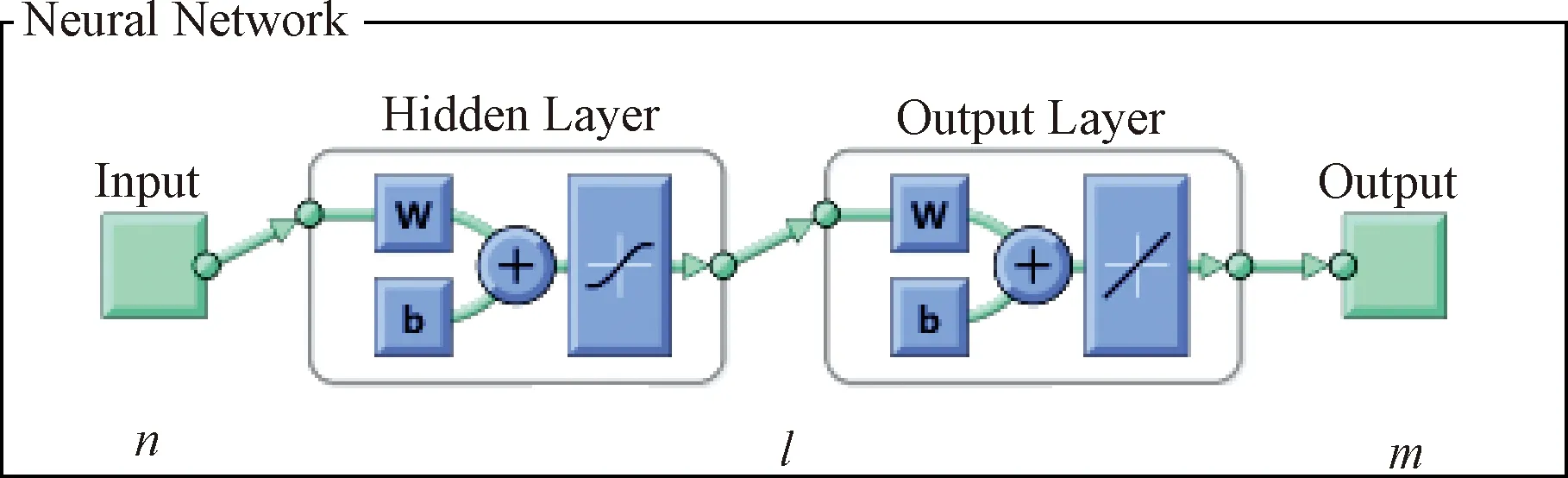
图2 BP神经网络连接示意图

其具体步骤如下：

Step1：网络初始化。确定必要的网络参数，一般有输入层节点数、隐含层节点数、输出层节点数、连接权值和阈值、传递函数种类等;

Step2：根据步骤1确定的各项参数，进行隐含层输出计算;

Step3：同上，进行输出层输入计算;

Step4：计算网络误差=期望输出-网络预测输出;

Step5：根据网络误差和网络学习速率，更新连接权值和阈值;

Step6：判断算法是否结束，若未结束，返回步骤2继续进行网络训练。

需要说明，一是传递函数有很多种，一般选用阈值型传递函数(hardlim)；二是网络数据在训练过程中需要的是归一化后的数据，这就要求在数据输入前进行(0，1)的数据归一化，在数据输出时再进行数据还原；三是一般来说，隐含层节点数需要人为确定，设输入层节点数为n，隐含层节点数为l，输出层节点数为m，满足以下关系：

(1)

2.2.2 RBF神经网络预测模型

进一步，由于BP神经网络在连接权值上一般需要反复迭代进行确定，对于大量数据处理过程会产生比较大的时延。而RBF径向基神经网络通过求输入样本和隐藏层点(中心点)的范数，将其代入径向基函数(高斯函数，二次函数，逆二次函数等)得到一个数值，再与之后的权值相乘加和，就得到了相应的输出，其网络简单，学习收敛速度很快。其总体的表达为：

(2)

式中：ω为连接权值，可通过最小二乘法迭代得到，计算式为：

i=1,2,…,h;p=1,2,…,P

(3)

具体的学习算法步骤如下：

Step1：使用K均值聚类方法求解径向基函数中心，一般经过网络初始化、将输入数据按照最近邻规则分组、重新调整聚类中心3步完成；

Step2：求解RBP神经网络径向基函数方差；

Step3：使用最小二乘法计算隐含层和输出层间的权值。

M国、E国和Z国从2009年至2019年电子战人员变化曲线如图3所示。可见，电子战人员的需求量随着现代战争发展以及国际形势变化会呈现出非单调的摆动发展序列或者具有饱和状态的S形序列，使用神经网络对其进行数据预测比较恰当。

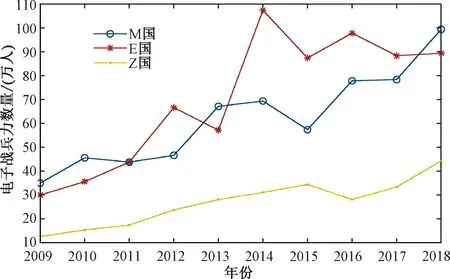
图3 M、E、Z国2009～2019年电子战人员变化趋势图

2.3 k级人员补充模型

对于电子战人员系统，一定是不断有人从中离开，因而要保持各类人员的数量必须进行人员补充(如招收新的人员以及人员的晋升等)。k级人员补充模型就是根据当前的人员分布、将来希望的人员分布以及离开人员的数量(比例)，计算晋升和招收的各类人员的数量。

用ni(t)表示在时刻t，i级的人员数；nj(0)表示在当前时刻j级的人员数；mij(t)表示在区间(t-1,t]内从i级转移到j级的人员数；ri(t)表示在区间(t-1,t]内从外部招收到i级中的人员数；mi0(t)表示在区间(t-1,t]内从i级离开系统的人员数(i=1,2,…,k；j=1,2,…,k；t=1,2,…)。

在此考虑具有k级的严格等级人员系统。由人员流动的平衡关系，由k-1级向k级晋升满足：

mk-1,k(t)=nk(t)-nk-1(t)+mk0(t)

(4)

在每级之间的mij(t)由各级间的晋升比例确定(编制、战斗力需求等因素影响)，则mk-1,k(t)与mk-2,k-1(t)均为已知量，可以得出递推关系：

(5)

可以发现，在调整i-1级人员比例时出现本级人员积压过多的现象，导致该级流出(包括离开机构以及向上级晋升)人员小于希望本级减少的人员数量，向i级的晋升m(i-1)i(t)会产生负值，显然不符合实际，对式(5)做出如下改进：

(6)

同样地，如果i-1级人员数量过小，需要晋升的人员数比原有数量还要多时，对式(6)做出如下改进：

(7)

这样，通过模型1将各个阶段电子战兵力大致数量确定，代入模型2中，将未来需要了解阶段内的电子战兵力人数进行预测，在模型3 中对电子战人员系统进行人员增减的具体讨论，就可以对电子战人力资源规划提供一个清晰的思路流程。

3 电子战人员补充算例预测与分析

以Z国电子战人员数据为例，进行电子战人员补充算例预测与分析。下面按照电子战人力资源规划流程，将原始数据(2009～2019)分为两部分，前10年数据为基础数据，第11年数据为验证数据，进行3个模型的求解，进而预测后一阶段的电子战人员数量，求解人员补充模型具体解。

3.1 Z国电子战兵力整体需求

在第1个模型中，首先将原始数据(2009～2018年Z国军事人员数量)进行初始化，按照军事战略发展和世界军事发展趋势等因素确定电子战兵力各阶段初始化数据，并且电子战兵力序列为(12.6,15.4,17.44,23.76,28.1,31.1,34.42,28.14,33.35,44.35,35.8)。如表1所示。

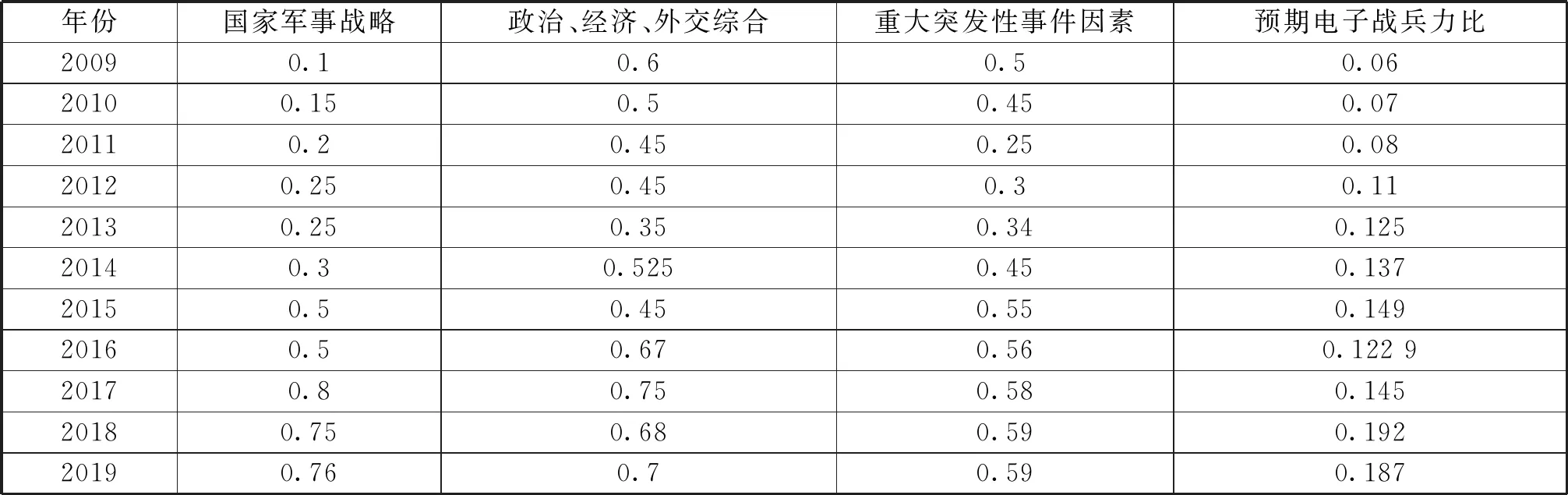
表1 Z国电子战兵力各阶段初始化数据

3.2 Z国电子战兵力神经网络模型预测

3.2.1 BP神经网络预测[5-6]

按照BP神经网络建立步骤，首先建立4-9-1结构的BP神经网络，如图4所示。

在结果的讨论中，我们加入决定性系数来讨论相对误差的大小。

设相对误差：

(8)

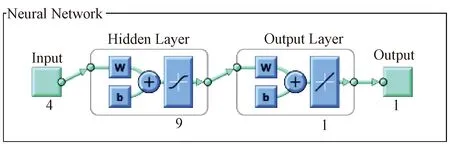
图4 Z国电子战BPNN模型结构

式中：Tsim为兵力预测结果；Ttest为兵力实测结果。

决定性系数为：

(9)

3.2.2 RBF神经网络预测

按照RBF神经网络的建立步骤，同BP神经网络数据处理相类似建立模型。

节点的径向函数φ为高斯函数：

(10)

式中：‖·‖取欧式范数;c为函数中心;σ为函数方差，求解方法为：

(11)

通过以上方法，代入模型1求的相关数据，得到表2结果。

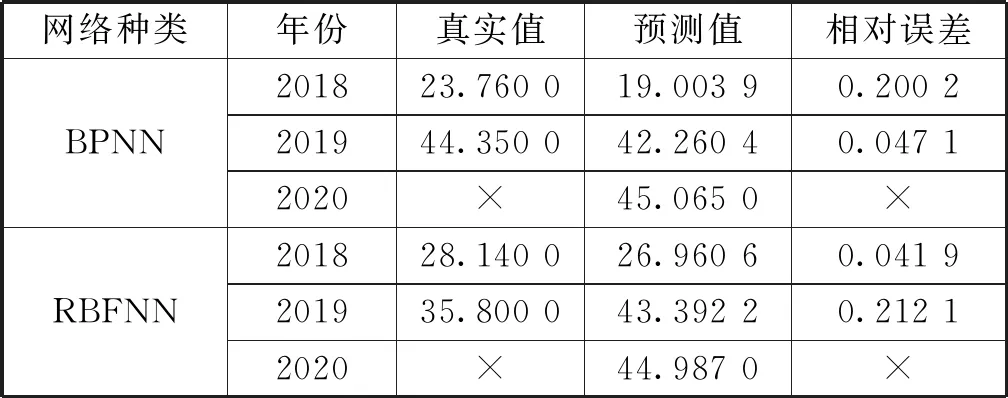
表2 Z国电子战人员神经网络预测数据

在BP神经网络预测的训练测试误差和总体误差(9组数据)进行误差分析，其决定性系数拟合值变化图像如图5所示，图中横纵坐标分别表示输入样本数据和预测数据的误差值，若以Y代表预测误差，两者的误差拟合方程分别为：

Y1=0.92·A+0.041

(12)

Y2=0.83·A+0.12

(13)

式中：A为当前样本在总样本中所占比例。

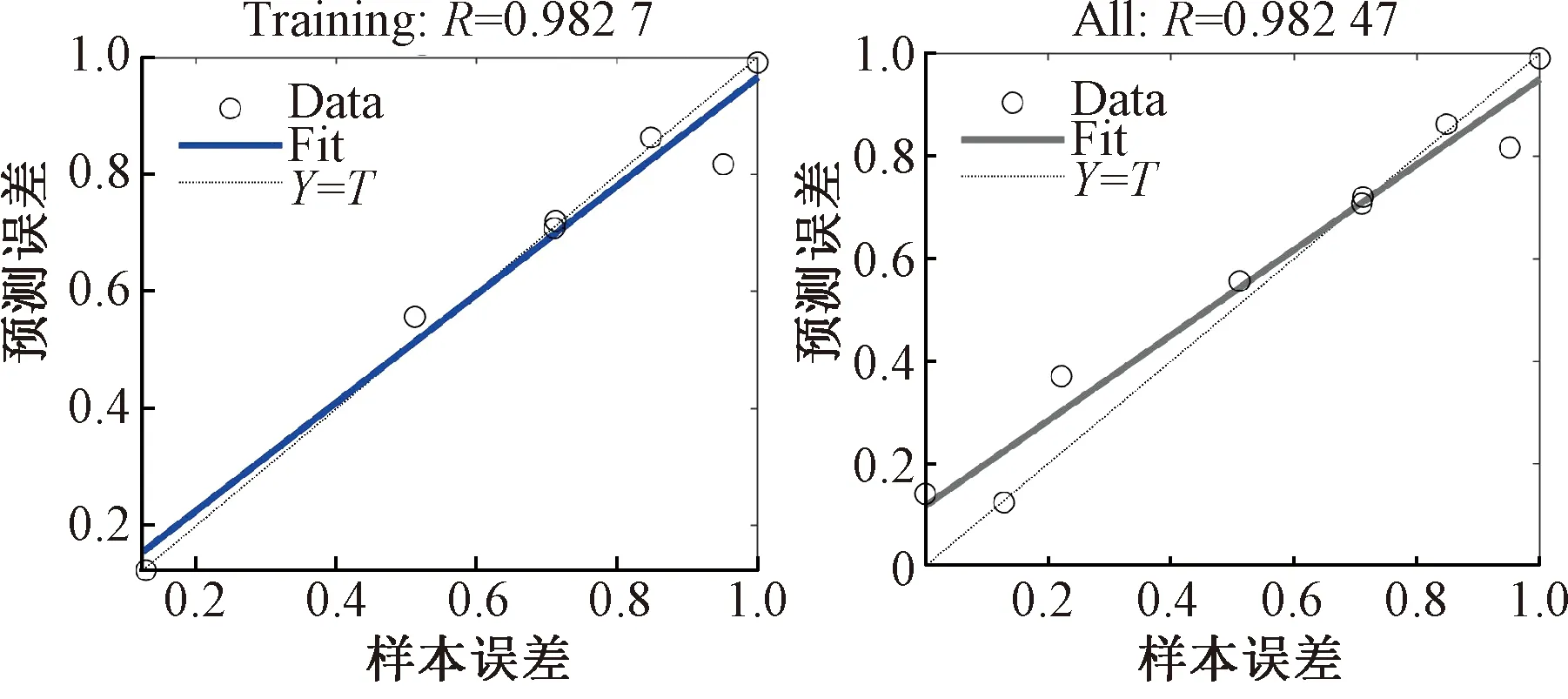
图5 误差决定性系数变化

可见，2种神经网络在具体算例计算过程中相对误差比较相近，但对于遇到大数据样本时，BP神经网络由于反馈迭代连接权值过程比较耗时，此时RBF神经网络就会更节约时间。

3.3 Z国电子战兵力k级人员补充需求

按照模型2预测出Z国2020年度电子战兵力数量取45.065 0万人，代入模型3中进一步求解人员补充需求。

假设Z国电子战兵力系统有4级，各级之间人员需保持3∶1的数量关系，则可得出各级人员序列为nj(t)=(30.417 4,10.139,3.380,1.127)，模型3满足：

(14)

解得:m10(t)=47.36,m20(t)=21.43,m30(t)=8.91，m40(t)=3.86，r1(t)=74.86。

这样，就得出了Z国在2020年电子战兵力的预期需求，获得了实际电子战兵力结构中各级的晋升、退役大致人数，可以为兵力整体规划提供很好的决策依据。

3.4 几点说明

通过以上算例，说明整个电子战人力规划十分有效，可以为指挥员提供很好的决策依据。但还存在几点不足：一是整体规划流程在模型1中考虑了突发事件的影响，在另外2个模型中考虑的还不够细致；二是k级人员补充模型中表示的严格等级系统只允许第1级直接从外部招收人员。而实际上等级系统也需要在其他级直接招收新的人员(比如对特殊电子战人才的招收和战时的紧急动员)，这样进入某级的人员就会分为下级晋升和外部招收两部分，等级就会拓展为非严格的等级系统，可运用各级之间的人员转移矩阵进行关系表示，运用马尔科夫转移网络也可以得出相应结论，有待进一步讨论。

4 结束语

在未来智能化联合作战中，电子战必定是左右战争胜负的关键一环，而电子战人力资源规划就显得尤为重要了。而目前对于这方面的研究很少，基本停留在定性分析上。本文立足于以往人员数据和经验结论，运用2种神经网络进行模型分析和数据预测，为电子战人力资源规划提供了一个切实可行的定量分析方法。经实际数据演算，该方法的确能够对电子战人力资源规划起到辅助决策的作用。