基于热线法的不同水分含量松散煤体热物性实验与模拟研究*

曲国娜，贾廷贵，娄和壮，强 倩，郝 宇

(1.内蒙古科技大学 矿业与煤炭学院，内蒙古 包头 014010；2.北京城市排水集团有限责任公司，北京 100000；3.重庆工程职业技术学院，重庆 402260)

0 引言

采空区松散煤体对氧气的吸附作用导致热量集聚不宜消散，促使松散煤体热膨胀性增加[1-3]，造成松散煤体与氧气更大面积接触，促进煤自燃的发生和发展。松散煤体热物性参数对掌握煤自然氧化规律以及对矿井采空区煤自燃火源定位、煤自然发火预测起着重要参考作用[4-6]，并对采空区温度场产生直接影响。目前对松散煤体热物性参数测定主要包括稳态圆筒法[7]、非稳态平面热源法[8]、非稳态热线法[9-11]等，这些实验手段对松散煤体热物性参数的测试虽已取得一定成果，但由于测试周期长且与实验误差大等原因未能对松散煤体热物性参数进行准确测定[12-13]。Sassi等[14]以铂丝作为热线，利用热线法对多孔介质结构的有效热导率进行测量；陈清华等[8-9]采用自制物性参数测试系统，得出热物性随温度、含水率等因素的变化特征；唐明云等[15]采用平行热线法对松散煤体的导热系数进行测定；杨建蒙等[16]采用Fluent数值的方式对温度场的分布特征进行反演。上述研究对松散煤体热物性的测试均采用单一的热线法，本文综合考虑交叉法和平行法各自的特点进行研究，使用交叉法测定实验煤样的热导率，平行法测定实验煤样的扩散率；通过构建测试装置实验平台，对松散煤体热物性参数进行准确测量及计算，对不同水分含量下松散煤体导热系数的变化规律进行研究，结合Fluent数值模拟软件对松散煤体温度场进行模拟，并对比模拟与实验结果的差异性。

1 数学模型

利用交叉热线法测得松散煤体导热系数λ，在松散煤体中放置1根细长热线，其直径相对于松散煤体介质无限小，在某一时刻产生的热量为q，在经过任意时间t后的任意位置(x,y)的温升为T，计算如式(1)所示：

(1)

式中：T为温升，℃；ρ为密度，kg/m3；Cp为比热容，kJ/(kg·℃)；a为热扩散率，m2/s；x为位置横坐标，m；y为位置纵坐标，m；t为从热线位置点 (x0,y0)到测温位置点(x,y)所需的时间，s；q为热量，kJ，可通过电流I及其电阻R表示，如式(2)所示：

(2)

式中：L为热线长度，m；I为通过热线的电流，A；R为热线电阻，Ω。

当线热源以恒定热流q持续加热时，从0到t时间段内，试样中距热线垂直距离为r的某一点(x,y)对于初始点(x0,y0)的温升计算如式(3)所示：

(3)

式中：λ为导热系数，W/(m·℃)，λ=aρCp；r为距热线径向距离，m，r2=x2+y2。

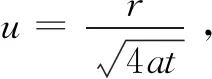
(4)

式中：Ω(u)为对时间t进行拉普拉斯变换后升温中的指数积分函数。

进一步得到式(5)：

(5)

(6)

式中：γ为欧拉常数，取0.577 26。

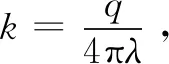
(7)

利用热线上的温升数据结合交叉热线法测得松散煤体导热系数λ，同时测得距热线r处的温升T，代入式(4)得式(8)：

(8)

令u2=p则有式(9)：

(9)

参照文献[6]中的各项数据，式(9)取5项得式(10)：

(10)

式(10)为超越方程，结合Matlab数值计算软件求出热扩散率a，通过若干个时刻对应的热扩散率得1组a值，取其平均值作为终值。

比热容Cp计算如式(11)所示：

(11)

2 实验准备

2.1 煤样制备与实验参数

选取神东补连塔长焰煤进行热物性实验，煤样工业分析见表1，对长焰煤煤样进行预处理，将取自井下的新鲜煤样袋装密封送至实验室，开袋后取出块煤的中心部分，粉碎研磨并筛选出1～2 mm，0.5～0.6 mm和0.2～0.3 mm 3种不同粒径的煤样，每种粒径的煤粉筛选10 kg，按不同粒径分成3组18份，以备实验所需。采用水雾喷淋和台式电热恒温干燥箱干燥的方法制备5.12%,7.50%,11.73%,13.88%,17.72%和20.05% 6种不同水分含量的实验煤样。

表1 神东补连塔长焰煤煤样工业分析Table 1 Industry analysis on coal sample of long flame coal in Shendong Bulianta %

2.2 实验装置

实验装置结构如图1所示，采用平行热线法与交叉热线法结合方法对松散煤体热物性进行测定。煤样筒为高400 mm，内径210 mm的圆柱形筒，内部填充硅酸盐隔热棉绝热材料，具有较好的隔热保温效果。数据采集与传输系统采用PLC+热电偶的方式，采用西门子S7200系列PLC进行热电偶测量信号的转换与传输，利用PC/PPI编程电缆进行通讯，选用T分度高精度铠装测温热电偶。选择DY3500E型高精度可调直流稳压电源对加热棒进行加热，设计加热棒直径3 mm，长300 mm，人工用6位半精度万用表测定加热棒电阻，测试系统软件自动换算加热功率。

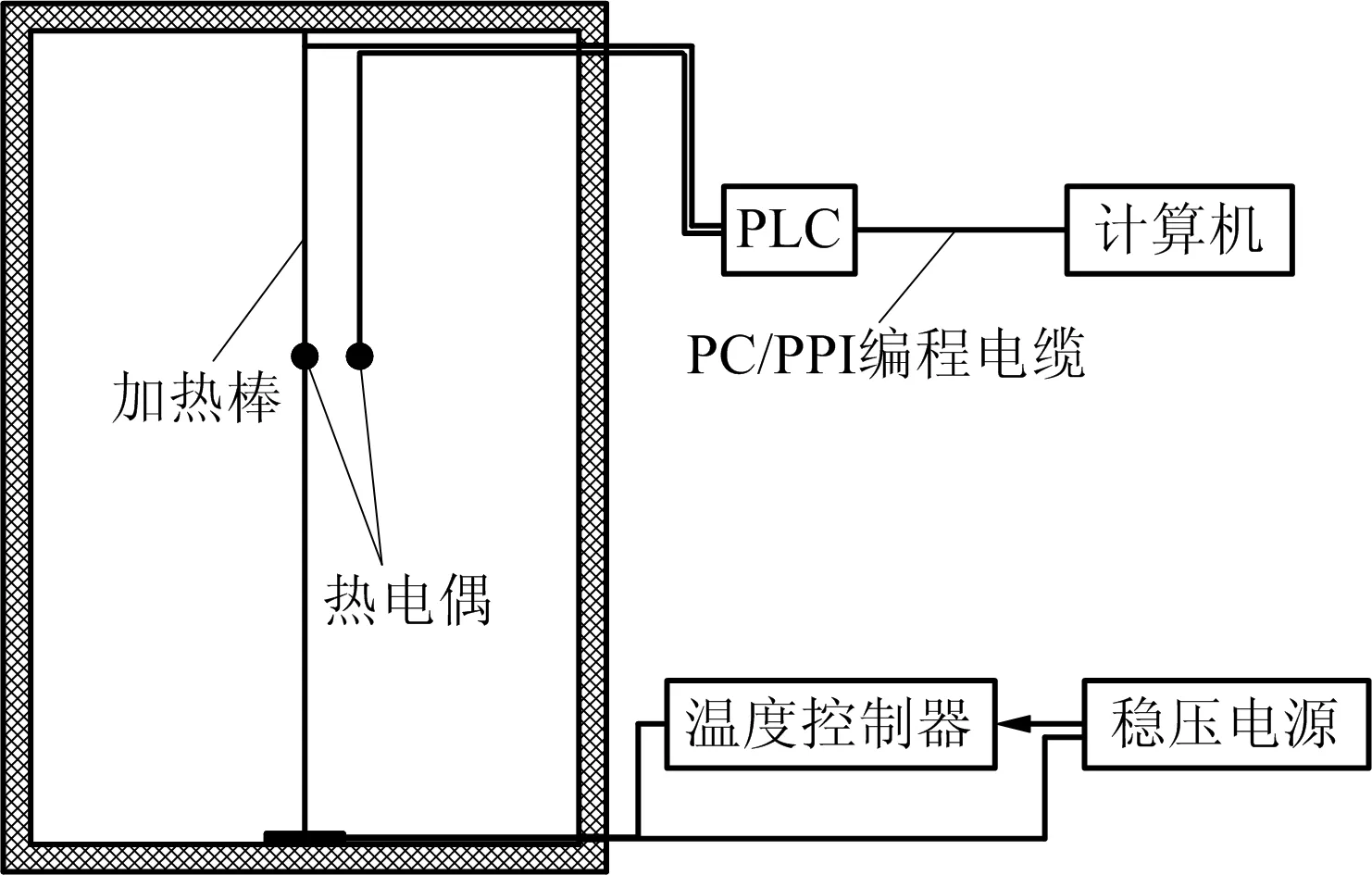
图1 实验装置结构示意Fig.1 Schematic diagram of experimental device structure

2.3 实验操作

对神东补连塔长焰煤3种不同粒径不同水分含量的实验煤样进行热物性实验，将测试煤样装入试样内筒中，采用高精度电子秤测量出煤样质量并计算出每次实验煤样的填充密度。调节温度控制器，待测煤样内筒中热电偶采集温度与环境保持一致，且5 min内波动不超过±0.1 ℃，打开直流稳压电源加热，加热功率10.50 W/m。实验120 s后开始收集并记录数据，间隔1 min读取1次计算机显示数据，采集10个有效实验数据后，结束数据收集并停止实验，并进行热物性分析的计算，测得导热系数λ和热扩散率a,计算得出比热容Cp。

3 实验结果

对煤样的温升-时间对数关系曲线图进行一元线性回归分析，拟合得出直线斜率k，根据式(7)计算不同粒径煤样的导热系数。实验测得松散煤体导热系数随水分含量的变化如图2所示。由图2可知，松散煤体的导热系数随水分含量的增加而增势渐缓。松散煤体的水分含量大小对其内部热流变化产生深刻影响，松散煤体内的水分通过潜热发生相变，导致其自身导热能力的改变[17]，水分含量的增大使得松散煤体导热能力得到大幅提升，一方面，随着松散煤体水分含量的增加，其内部热流在煤颗粒与气体之间接触面的汇聚效应减弱，减小接触热阻使得松散煤体导热能力得到整体提升。随着松散煤体的水分含量上升，水的导热系数逐渐增加，由于水的导热系数大于固体煤颗粒的导热系数，使得松散煤体的导热系数增加幅度缓慢。同时，在所测粒径范围里，同等水分含量下的松散煤体粒径越大导热系数越小，这是由于松散煤体粒径的增大使得煤粒间空气占比增加，而空气的导热系数较小，导致松散煤体导热系数减小。

图2 松散煤体导热系数随水分含量的变化Fig.2 Change of thermal conductivity of loose coal with moisture content

根据式(10)并结合Matlab软件计算不同粒径煤样的热扩散率，松散煤体热扩散率随水分含量的变化如图3所示。根据式(11)计算不同粒径煤样的比热容，松散煤体比热容随水分含量的变化如图4所示。由图3～4可知，松散煤体热扩散率随着水分含量的增加而增大，当水分含量达到11.73～13.88%后热扩散率开始逐渐下降，而比热容随着水分含量的增加逐渐增大，根据式(11)，在松散煤体水分含量较小的情况下，随着煤水分含量的增大热扩散率增加，但当松散煤体水分含量较大的情况下，因导热系数的增加幅度缓慢，而比热容仍随水分含量增加而增加(但实验中1.0～2.0 mm大粒径煤样略有不同，这是因为当水分含量小于14%时，符合比热容随水分含量增加而增加规律，且趋势明显；当水分含量在14%～18%时，该增加趋势变缓；当水分含量大于20%呈回落趋势。)，故此松散煤体热扩散率反而下降。同时，在所测粒径范围里，同等水分含量下的松散煤体粒径越大，热扩散率与比热容越大。由于煤体表面存在侧链结构，煤中水分含量的增加，使得其受热后做分子热运动剧烈，从而引起消耗的能量增加，导致比热容增大。而在同一水分含量下，较粗粒径的煤样表面侧链结构繁多，虽然较细粒径的煤样表面面积大，但侧链结构较前者少，受热后的分子热运动缓慢，表现为随着粒径的降低比热容降低。

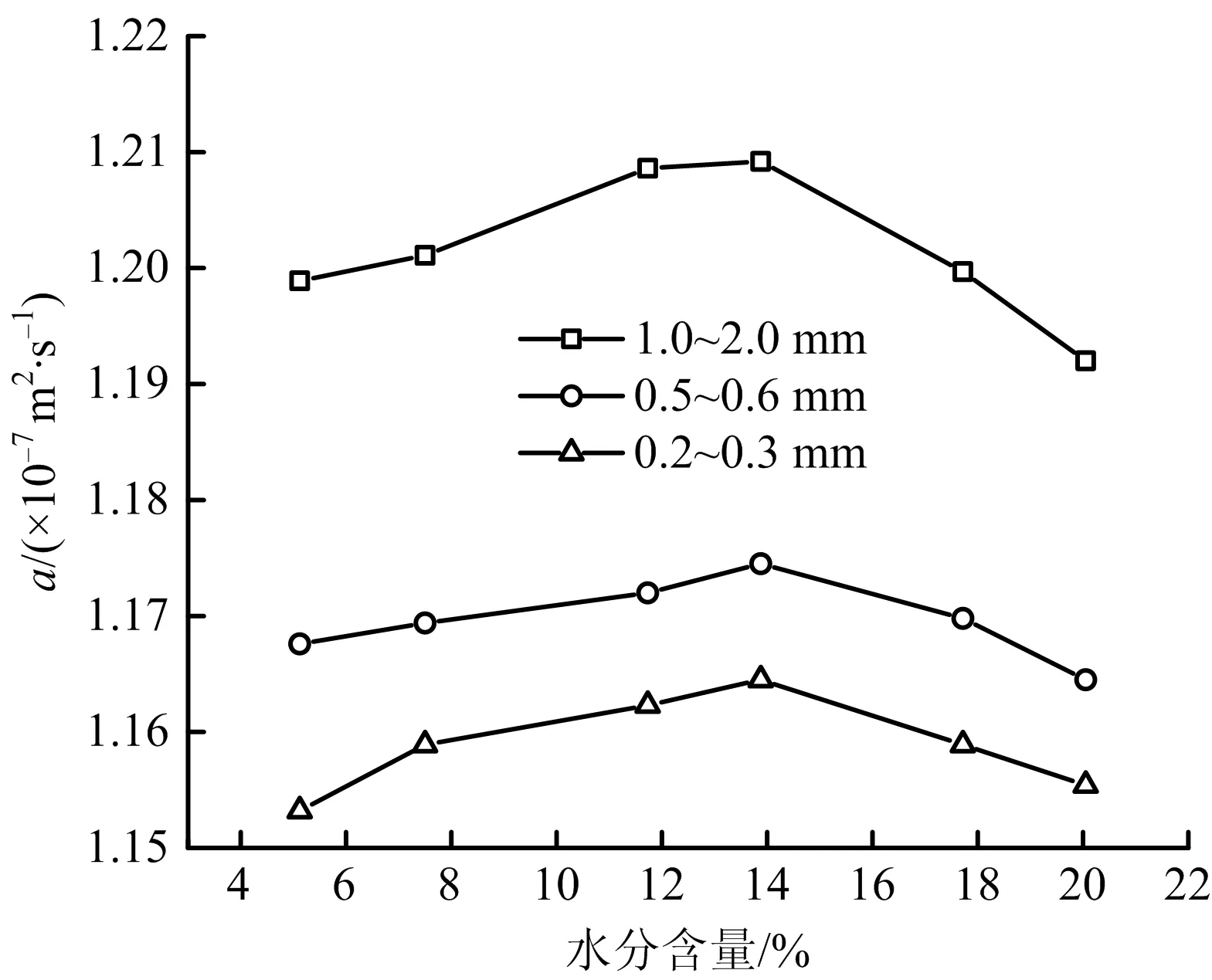
图3 松散煤体热扩散率随水分含量的变化Fig.3 Change of thermal diffusivity of loose coal with moisture content

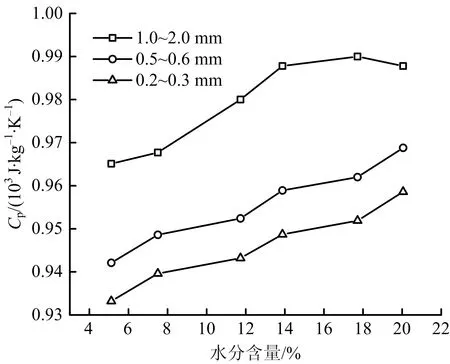
图4 松散煤体比热容随水分含量的变化Fig.4 Change of specific heat capacity of loose coal with moisture content

4 松散煤体温度场Fluent数值模拟

4.1 数值模拟模型

将实验装置简化为二维轴对称模型进行Fluent数值模拟计算，选取轴向截面一半为研究对象，松散煤体温度场数值模型如图5所示。煤样半径105 mm，高度300 mm，热线半径1.5 mm。热线定义为固体1，煤样定义为固体2，设置非稳态隐式格式求解器，非稳态热传导控制方程和其边界条件[16，18-19]如式(12)～(15)所示：

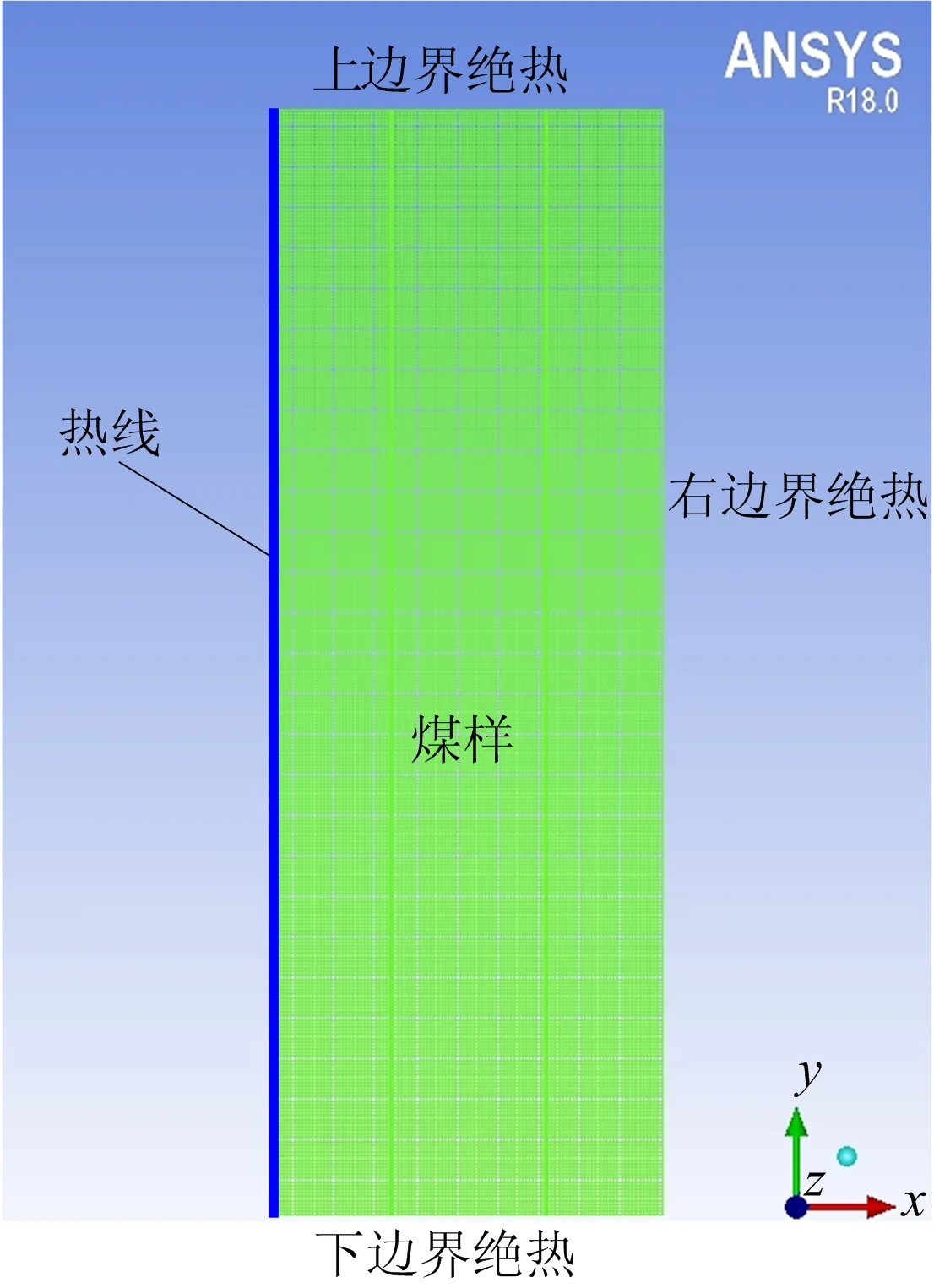
图5 松散煤体温度场数值模型Fig.5 Numerical model of temperature field of loose coal

(12)

(13)

(14)

Tt=0=T0

(15)

式中：R为煤样半径，mm；H为煤样高度，mm；Q为热源体密度，W/m3。

根据式(12)～(15)对建立的松散煤体温度场数值模型进行计算。采用结构化网格的四边形网格进行网格划分，左边界定义为axis，上、下、右边界定义为wall且绝热，划分得到totalelements=33 232，totalnodes=32 520。设置热线与煤样参数见表2，模拟初始温度290.65 K，热线功率10.50 W/m，加热时间750 s。

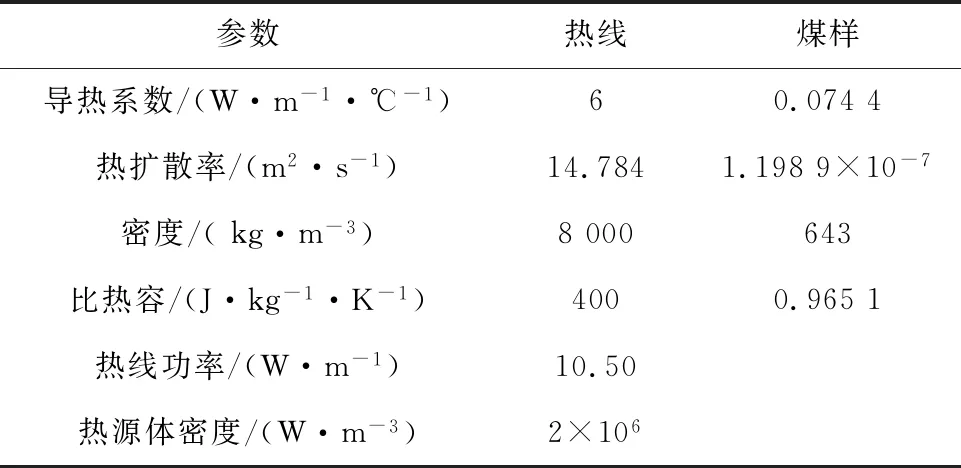
表2 热线与煤样参数Table 2 Parameters of hot wire and coal sample

4.2 模拟结果分析

神东补连塔长焰煤粒径1～2 mm，水分含量5.12%煤样热线温差数据见表3。通过Fluent数值模拟得到热线表面温度变化曲线如图6所示。

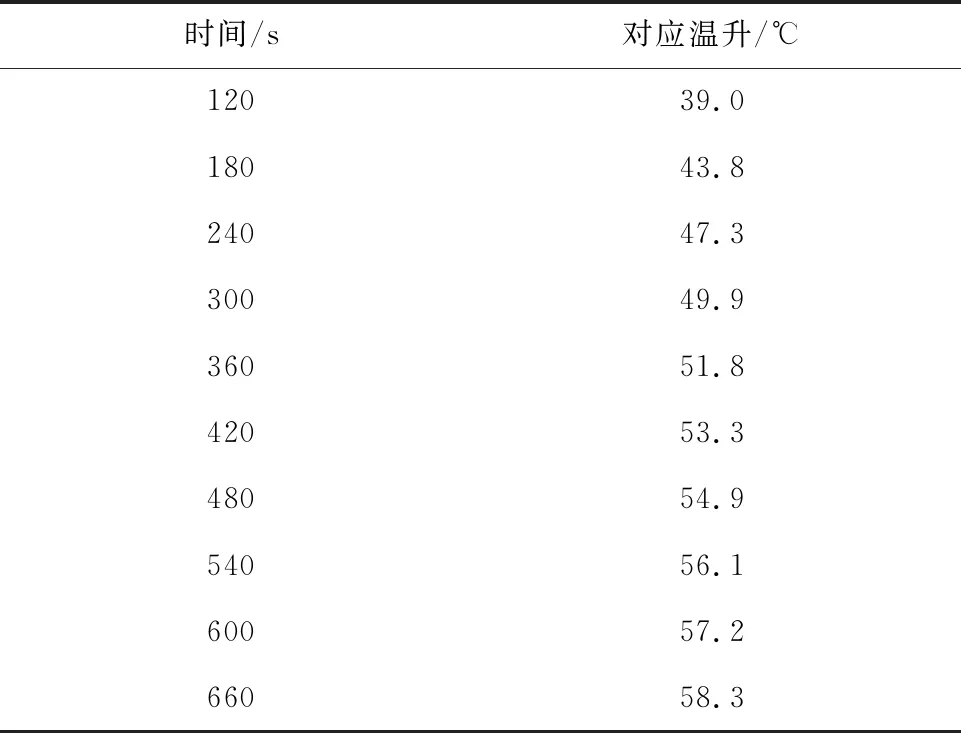
表3 热线温差数据Table 3 Temperature difference data of hot wire

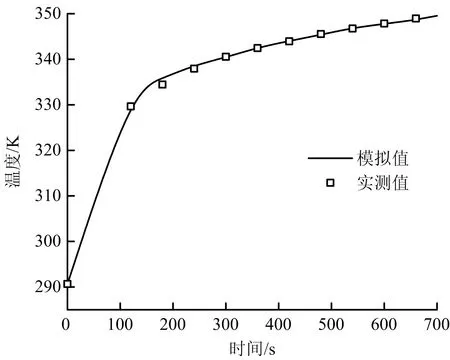
图6 煤样热线表面温度变化曲线Fig.6 Curves of temperature change on surface of coal sample hot wire

由表3和图6可知，模拟结果与实验结果契合度较高，可以相互印证，实验数据为理想数据，结论可靠。

5 结论

1)采用平行热线法与交叉热线法相结合的方法可对松散煤体热物性进行有效测定，在所测粒径范围里，同等水分含量下的松散煤体粒径越大，导热系数越小，热扩散率与比热容越大。

2)松散煤体的导热系数随水分含量的增加而增加，随着水分含量进一步增加，水的导热逐渐占据主导地位，松散煤体的导热系数增加幅度缓慢。

3)松散煤体热扩散率随着水分含量的增加而增大，当水分含量达到11.73～13.88%后热扩散率开始逐渐下降，而比热容随着水分含量的增加逐渐增大。