浮动堆设备闸门瞬态热固耦合数值模拟研究

(武汉第二船舶设计研究所，武汉 430064)

0 引言

浮动堆是国家海洋战略的重要工程之一，为海洋开发提供永续可移动能源的保障，是我国经略海洋的必然选择[1]。浮动堆在世界民用核能应用领域属于难度极高的工程，其相关设备安全性研究尤为重要。浮动堆设备闸门在事故工况下，与安全壳一起包容放射性物质，是安全壳压力边界较薄弱的环节。浮动堆设备闸门与陆上核电站不同，需要承受海洋环境引起的冲击、纵横摇摆载荷，更为复杂的是LOCA事故下安全壳内温度和压力相应引起的热应力载荷变化将更加剧烈[2]，在瞬态温度载荷下导致结构破坏的一个重要原因是来自结构不同位置的温度差[3]，而不单纯是最大的温度载荷，这种热应力足以使设备闸门产生过量的塑性变形或断裂[4]。

杜坤等[5]基于ANSYS有限元分析方案和法国RCC-M《压水堆核电厂机械设备设计和建造规则》的理论，分析设备闸门在内压、重力、地震等载荷组合的影响，开展了稳定性分析和法兰、螺栓的强度分析。钱浩等[6]开展人员闸门在温度、内压、重力等载荷下的强度评定，其中温度载荷采用了静态分析方法。施勣等[7-8]结合土建强迫位移，采用了等效静力的方法研究地震等载荷对人员闸门的影响。左树春[9]通过有限元静力分析法研究安全壳强迫位移造成法兰密封面分离及相对错动。采用热固耦合分析方法针对现有核电站设备闸门结构及密封安全问题的研究较少，而且均未考虑海洋环境下摇摆等特殊工况。因此，对设备闸门在事故工况下瞬态温度场以及相应的耦合热应力进行研究是具有实际意义的研究方向。

本文利用有限元方法求得瞬态温度场，结合事故工况下的压力、摇摆、冲击载荷，求得设备闸门耦合热应力，采用的分析方法可为其他浮动堆设备闸门的设计与安全评估提供参考和理论指导。

1 热应力问题基本原理

1.1 瞬态温度场有限元求解方程

求解瞬态温度场问题的核心是利用相应的数值方法求解线性常微分方程组，通过将经典热力学中结构三维瞬态温度场的控制方程进行推导，可以得出该问题以时间t为独立变量的线性常微分方程组[10]。

(1)

矩阵C，K，P的元素由单元相应的矩阵元素集成[11]，为：

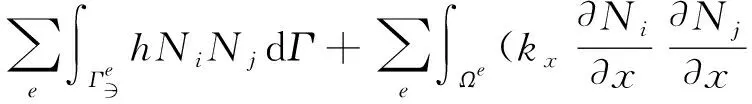
(2)

(3)

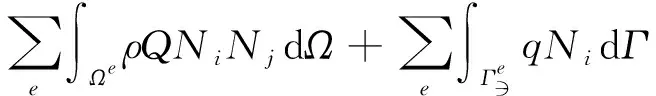
(4)

通过上式，可将时间域和空间域的偏微分方程问题在空间域内转变成N个节点温度φi(t)常微分方程的初值问题。

1.2 热-固耦合分析理论

热应力是温度场和应力场共同作用的结果，温度场和应力场互相作用的问题叫做热固耦合问题[12]，耦合结果满足物理方程、平衡方程和协调方程。热-结构分析计算的有限元方程[13]为：

(5)

式中，M为质量矩阵；u，T分别为位移、温度载荷；C为结构阻尼矩阵；Ct为比热矩阵；K为结构刚度矩阵；Kt为热传导矩阵；F为总等效结点力列阵；Q为总等效结点热流率向量。

2 耦合热应力的有限元分析

本文采用顺序耦合法进行分析，首先对设备闸门进行热分析，在得到瞬态温度场分布以后，将求得的节点温度作为体载荷施加到结构中，并利用给定的载荷和位移条件对耦合应力进行分析。

2.1 工况说明

浮动堆在正常运行工况，受到船体摇摆、自重作用，极端事故工况时，需要考虑受冲击影响下，LOCA事故的高温高压影响。LOCA是压水堆核电站的设计基准事故，当船用核动力装置发生LOCA事故时，大量高温高压流体从破口喷入安全壳，导致堆舱内温度和压力急剧上升[10]。由于前10 s出现温度及压力峰值，本文选取冷断断裂情况下前10 s的温度及内压进行分析。

正常运行工况下，安全壳内壁初始温度为50 ℃，外表面温度为22 ℃。冷断断裂情况下，安全壳内温度及压力变化如表1所示。其余设计载荷为摇摆载荷、冲击载荷、自重、压力、螺栓预紧力，如表2所示。

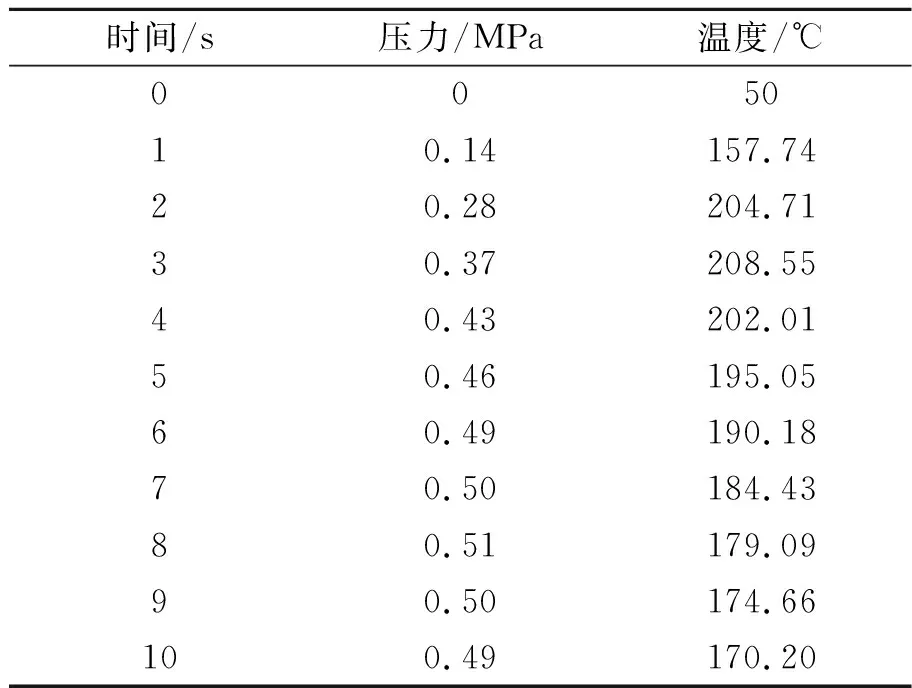
表1 安全壳内温度及压力

表2 载荷说明

在考虑船舶摇摆对换料盖的影响时，假设换料盖为一质点，摇摆的中心位于水线面、船舶中心线与船舯的交点处。将其运动函数简化为角位移函数[14]：

(6)

(7)

本文计算时，将角位移函数求解二阶导数[15]，将该载荷转化为瞬时加速度施加。摇摆运动加速度控制方程如下：

(8)

(9)

设备闸门上下法兰材料选用ASME boiler and pressure vessel code,sectionⅡ,Material D篇中的SA-738Gr.B级钢板，其热导率性能列于表3。

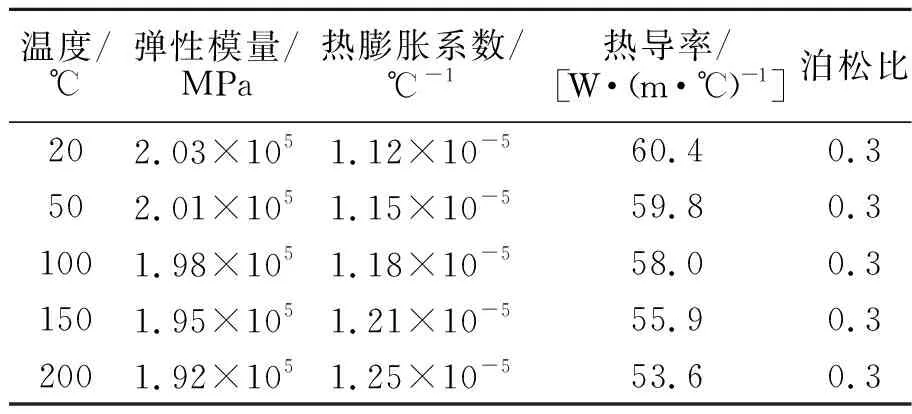
表3 SA-738Gr.B力学参数

设备闸门螺栓材料选用SA-193 B7。根据ASME boiler and pressure vessel code,sectionⅡ,Material D篇，当温度为158 ℃时材料基本力学性能见表4。

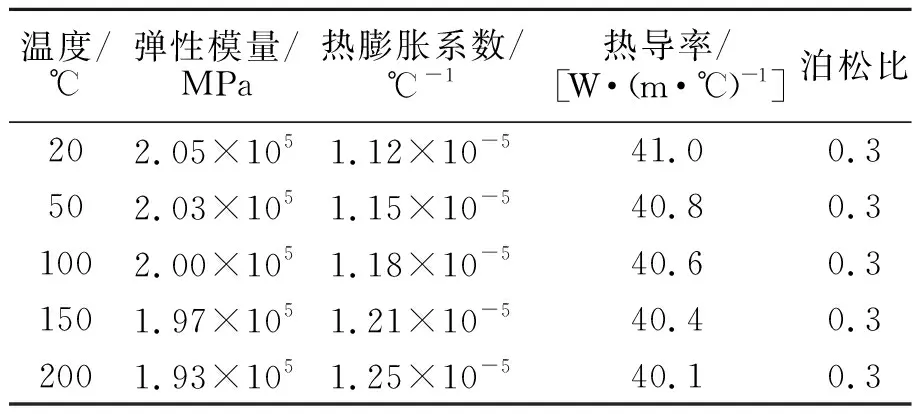
表4 SA-193 B7力学参数

2.2 建模及约束条件

本文采用有限元软件Ansys Workbench19.2进行模拟分析，分别建立设备闸门本体、主螺栓、筒体以及下法兰模型，并装配成为整体。计算模型中球面盖板、法兰和螺栓均使用三维实体单元Solid 186；法兰之间的接触及螺栓与法兰之间的接触采用接触单元Targe 170和Conta 174；螺栓预紧力采用Prets 179单元[16-17]，各处的摩擦系数取为0.2。在建模过程中，本文对结构进行了如下简化：

(1)结构中的密封垫片只作密封用，不是主要受力件，建模不予考虑，不作评估；

(2)设备闸门受摇摆和冲击载荷，具有1/2对称性，在保证计算精度的前提下，为减小计算量，采用1/2模型进行建模。

2.3 瞬态温度场计算以及应力计算

本文结构热固耦合分析分为3个阶段：第1阶段先分析设备闸门正常运行工况下热稳态温度场；第2阶段分析结构升温过程中的瞬时温度场;第3阶段把所得温度场作为体载荷施加到结构整体热应力分析中。

(1)第1阶段计算设备闸门热稳态分布。正常运行工况下安全壳内壁初始温度为50 ℃，外表面温度为22 ℃，与空气对流换热，换热系数为5×10-6W/(mm2·℃)。此时，设备闸门温度分布比较均匀，螺栓端部温度最低，与设备闸门内壁最大温差约为2 ℃，图1示出初始热稳态时设备闸门温度场分布。

图1 初始热稳态时设备闸门温度场分布示意

(2)第2阶段计算整个升温和降温过程的各瞬态温度场。冷断断裂情况下，设备闸门内表面经过3 s升温到208.55 ℃，随后逐渐降低至170.20 ℃。计算时，温度载荷的施加分为10个载荷步，设置结束时间10 s，采用子部设置，每一子步计算10个瞬态热结果，开启时间积分设置。

图2是第3 s瞬时温度峰值时温度场分布。此时设备闸门由内表面至外表面呈现较为陡峭的梯度分布，特别是在内表面区域温度变化最大。可见,在安全壳内突然升温时，由于热量不能快速传递至外表面，形成热量在设备闸门内表面堆积的情况。

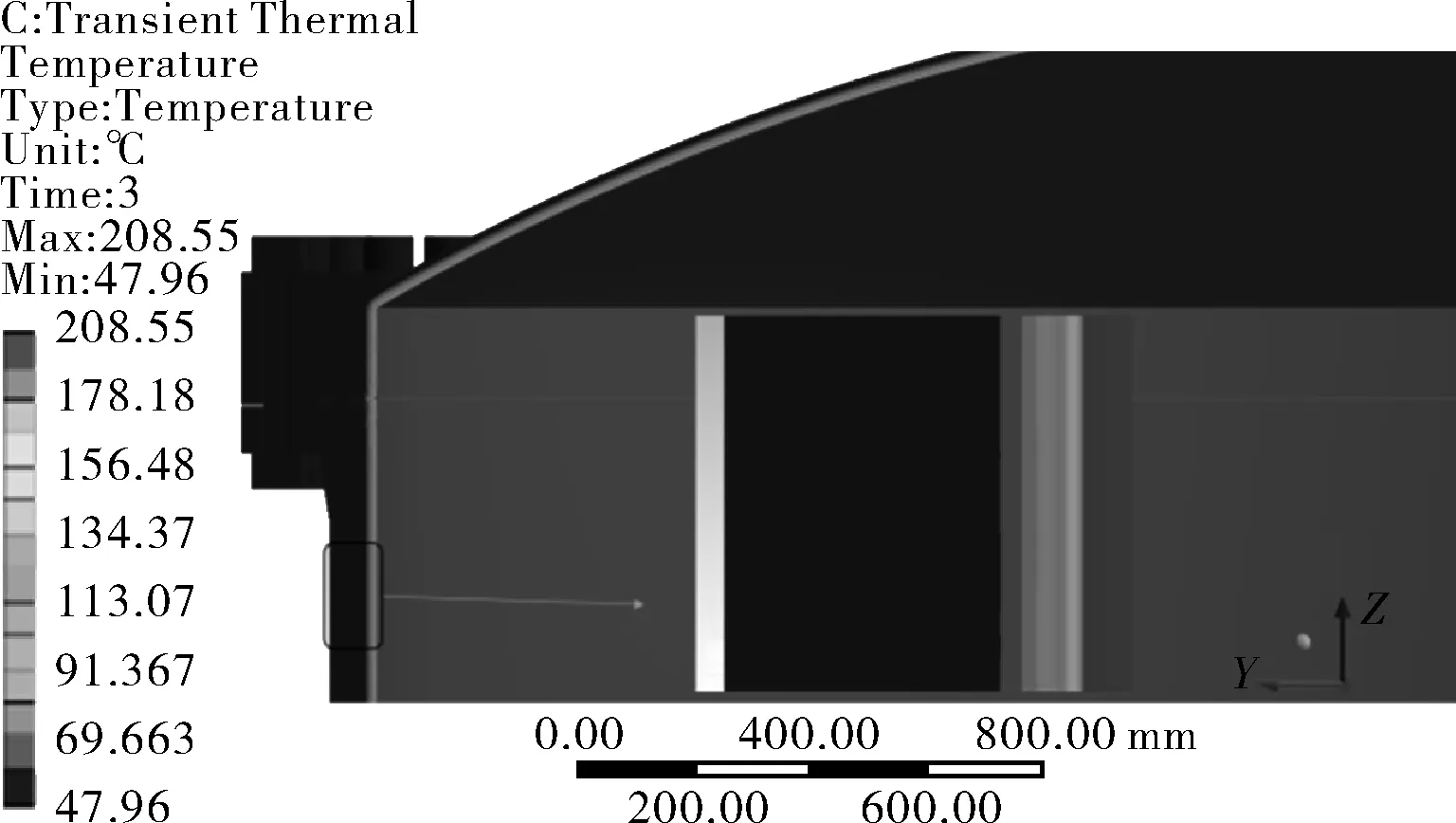
图2 第3 s瞬时温度峰值时温度场分布

表5示出设备闸门内外密封面、封头外表面、螺杆及螺母的温升情况。在10 s内，内密封面和球壳外表面温度变化要大于其他区域，温度差引起的热应力影响也应大于其他区域。

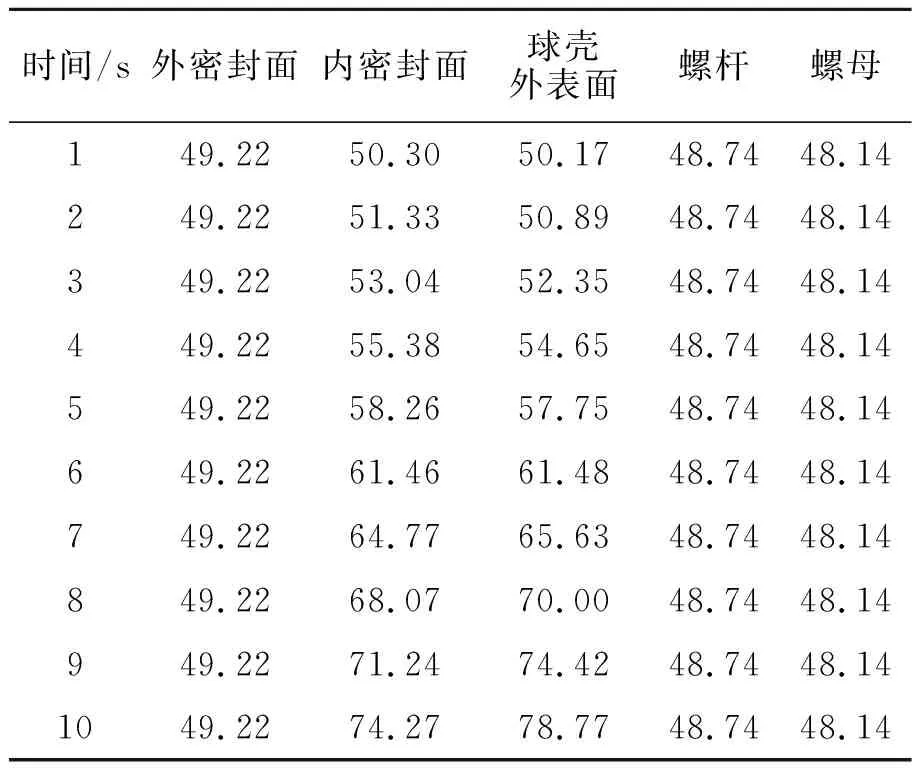
表5 设备闸门各区域温度

(3)第3阶段将所得的节点温度映射到结构中，并结合给定的结构应力和位移条件求解。图3是设备闸门在第3 s时，设备闸门von Mises及周围典型螺栓应力云图。由于设备闸门需要承受摇摆、冲击等不均匀载荷影响，因此，选取设备闸门周边5个典型位置作为应力监测点。

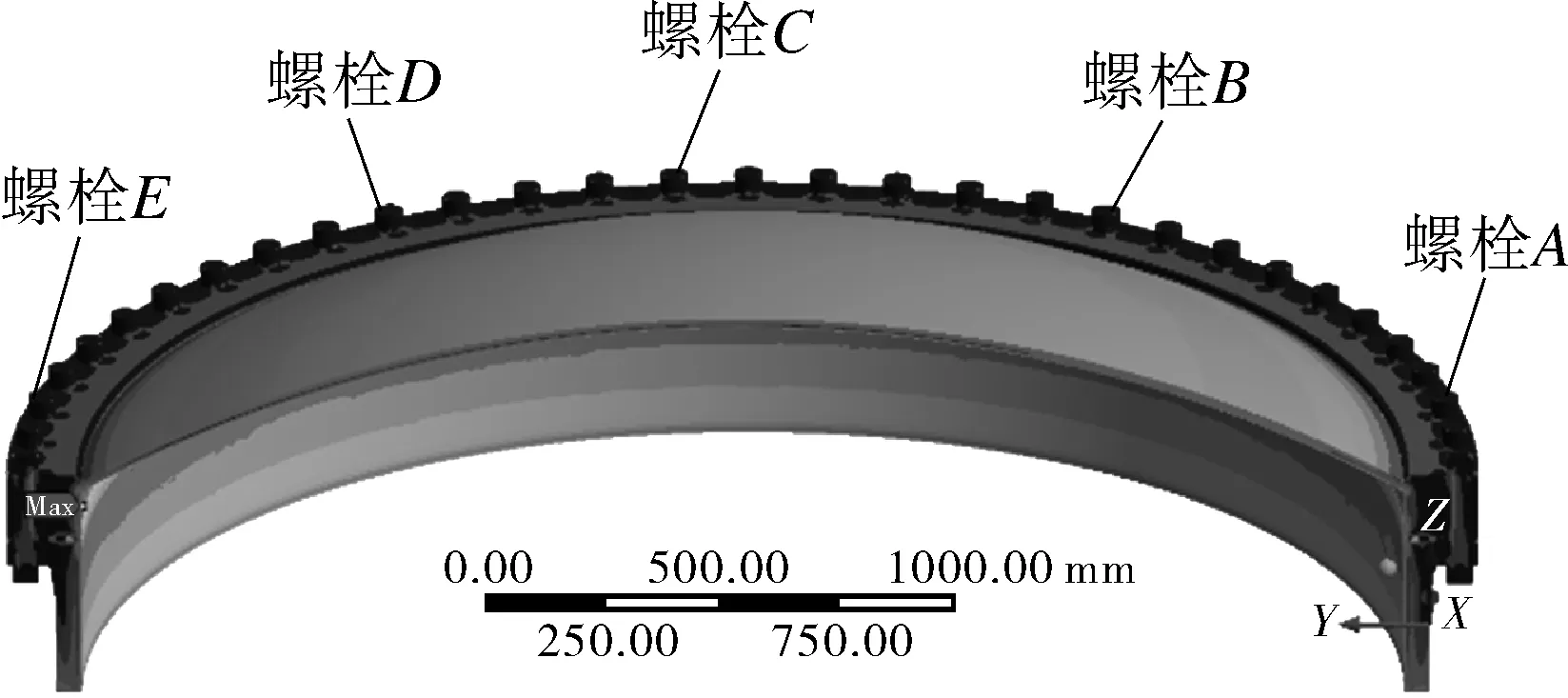
图3 第3 s时von Mises应力云图

表6示出设备闸门球面盖、下法兰、螺栓A、螺栓B、螺栓C、螺栓D、螺栓E的von Mises应力时程。可以看出，设备闸门球面盖、下法兰应力变化随温度变化明显，螺栓由于温升量较小，应力变换随温度变化不明显，出现峰值应力的时间点并不相同。球面盖、下法兰最大von Mises应力发生时间为3 s，最大值为452.87 MPa及429.35 MPa，螺栓B的von Mises应力较其他螺栓高，发生时间为8 s，最大值为214.54 MPa。

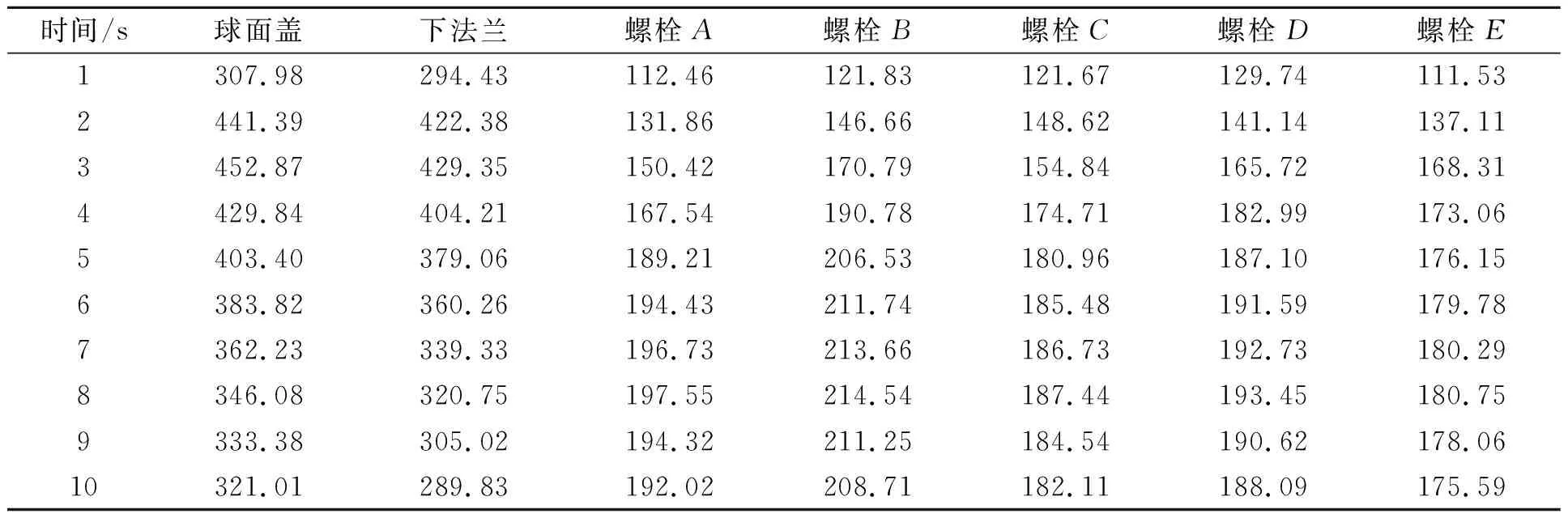
表6 设备闸门各部件von Mises应力时程

考虑瞬态温度载荷后，设备闸门整体von Mises应力明显增大。与采用稳态热应力计算相比，采用瞬态热固耦合方法可以更为准确地反映设备闸门内部结构温度分布，分析出由于球面盖及下法兰和螺栓最大von Mises应力发生时刻，从而更为精确地分析设备闸门在复杂海洋环境中的安全性能。

3 结构耦合热应力有限元结果分析

3.1 结构耦合热应力结构影响分析

基于ASME boiler and pressure vessel code,section Ⅲ,Rules for construction of nuclear facility components中表NE-3221-1应力强度限制的要求，采用第三强度理论校核设备闸门结构强度进行校核。分别在球面盖、法兰及螺栓前10 s最大等效应力处开展应力分类评定，分离出一次总体薄膜应力Pm、弯曲应力PL+Pb、二次应力PL+Pb+Q，如图4～7所示。

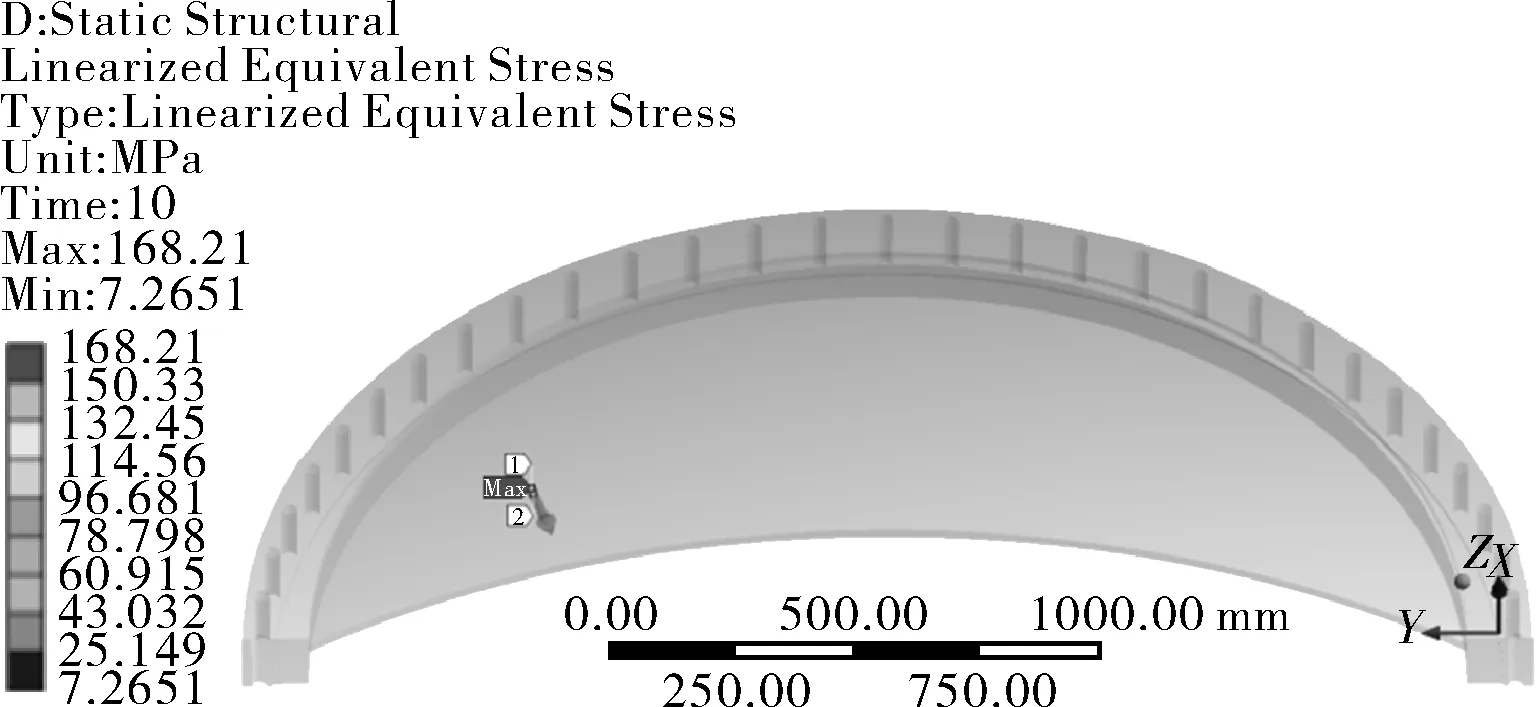
图4 球面盖封头应力线性化路径G01

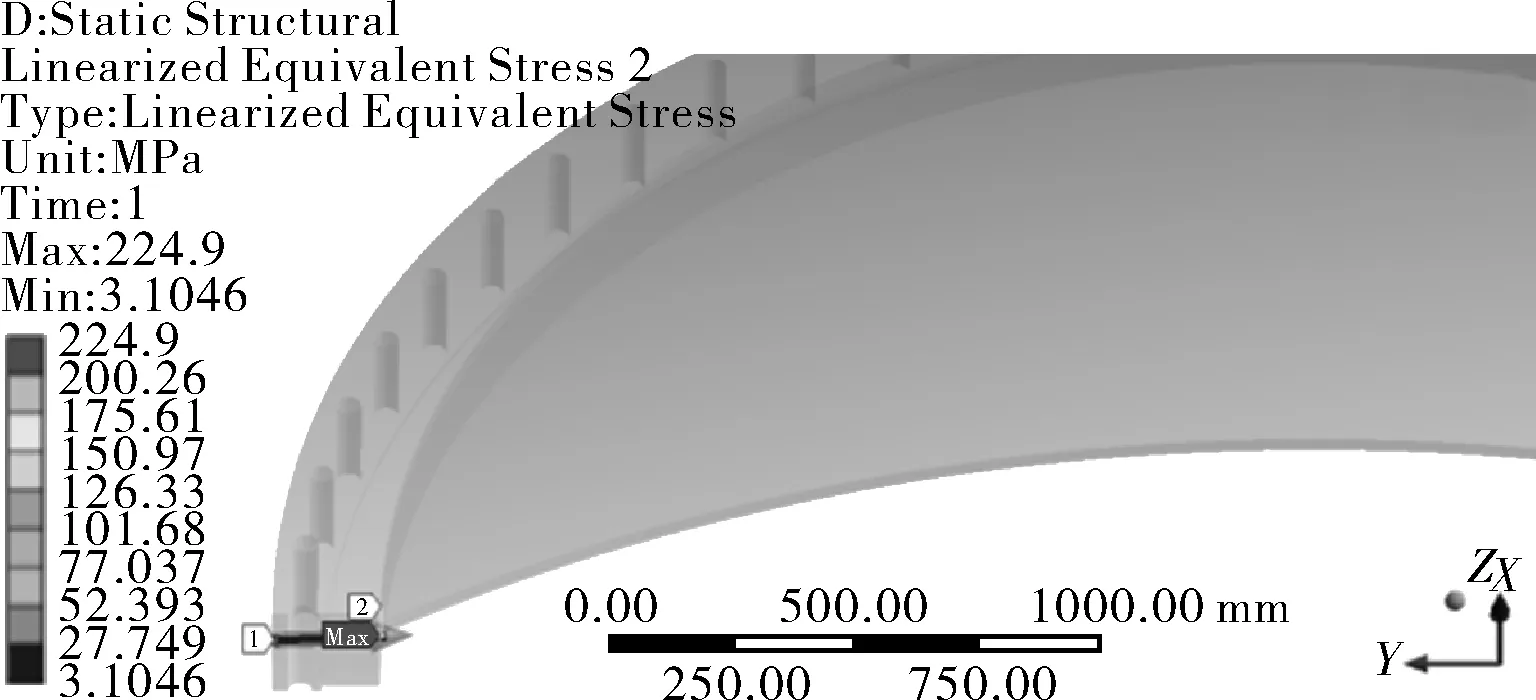
图5 球面盖上法兰应力线性化路径G02

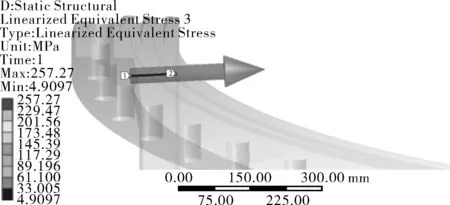
图6 下法兰应力线性化路径F01

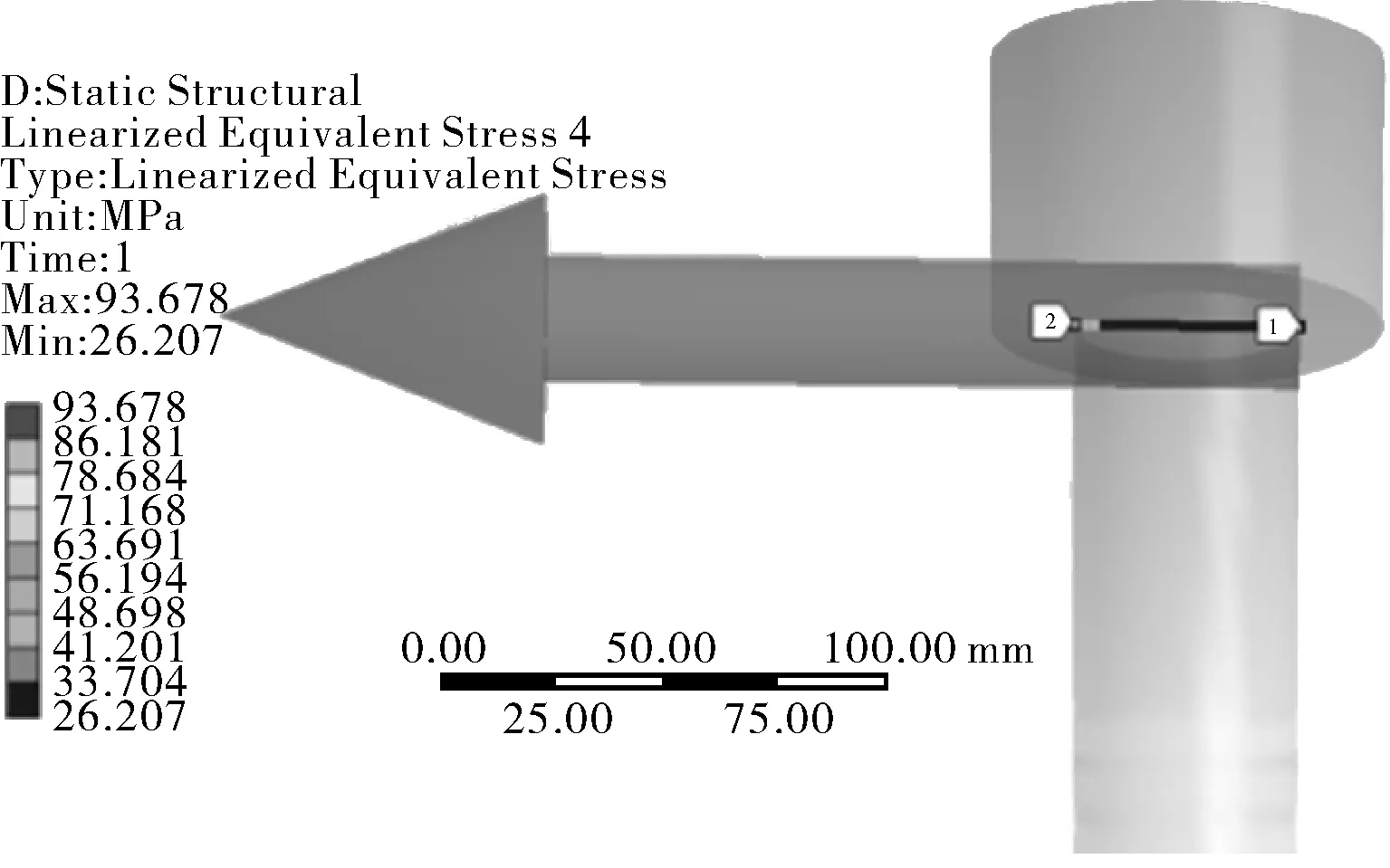
图7 螺栓应力线性化路径L01

采用瞬态热应力载荷开展应力评定时，应考虑全时间周期内线性化路径上的应力变化。球面盖在3 s时von Mises应力最大，应予以重点考虑。

图8示出10 s内球面盖法兰弯曲应力值，可以看出球面盖法兰G02两端的弯曲应力变化较内侧大，受温度载荷影响，内侧弯曲应力在0～3 s时快速升高，随后变化趋于平稳，在10 s时达到峰值，完全应力最大值为93.82 MPa，整体变化趋势与内压变化相近。

图8 0～10 s球面盖法兰弯曲应力值云图

图9为10 s内球面盖封头二次应力值，在0～2 s时封头内表面二次应力快速升高，达到峰值148.89 MPa，而后逐渐降低。同一时刻封头内表面受温度载荷影响，内表面二次应力值要明显大于其他区域。图10,11示出10 s螺栓平均应力和最大应力值云图，在3 s前螺栓平均应力和最大应力值增速明显，在第8 s时，平均应力和最大应力值均达到最大值，整体变化趋势与内压变化相近。综合考虑整体瞬态温度分析，可以确定在设备闸门内侧区域，由于结构温度差产生的热应力而引起的应力变化占主导地位，必须予以重视。

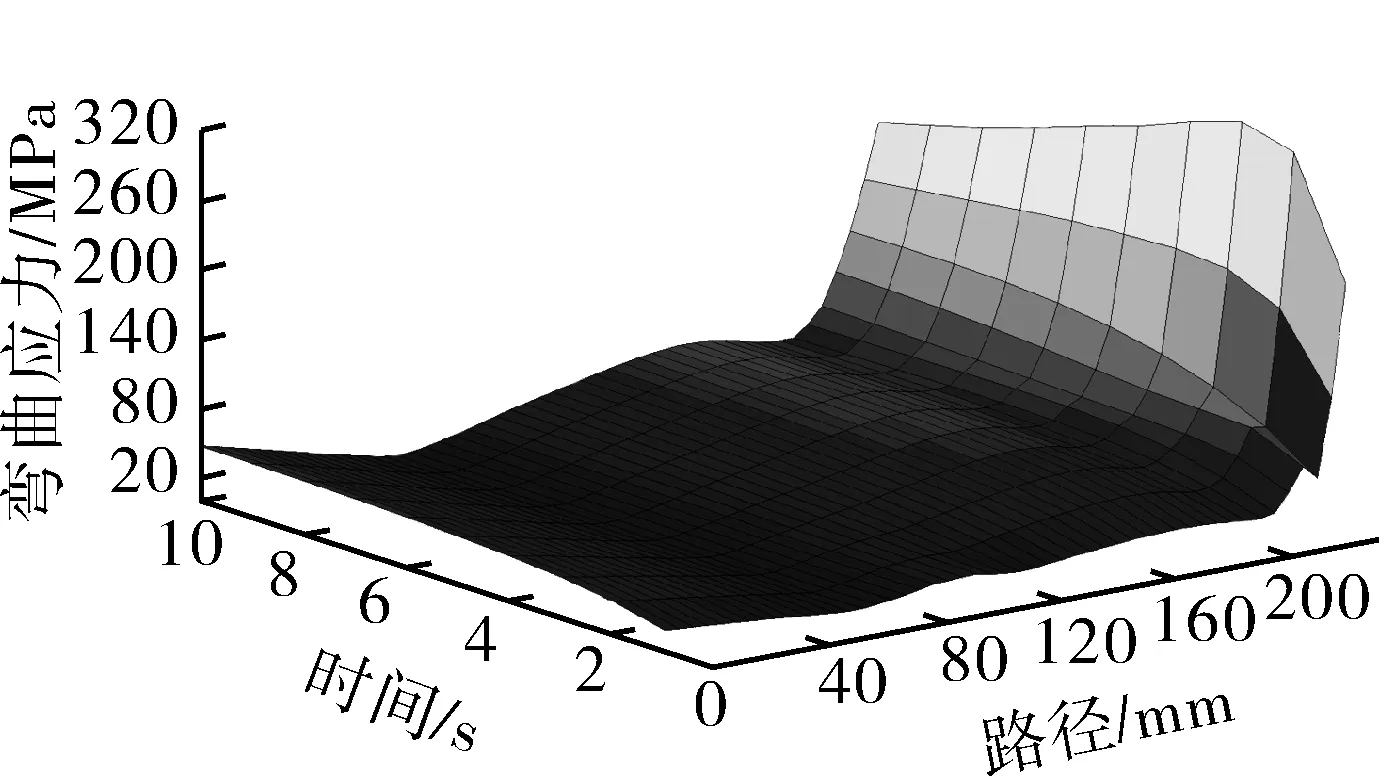
图9 0～10 s球面盖封头二次应力值云图

图10 0～10 s螺栓平均应力值云图

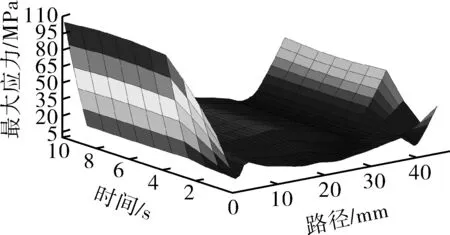
图11 0～10 s螺栓最大应力值云图

表7示出设备闸门应力分类评定结果，在第4 s时球面盖封头完全应力比值达到95.91%，可以认为在该时刻，设备闸门处于最危险状态，应针对该区域进行加厚处理或采用隔热涂层等措施，以降低热应力的影响。

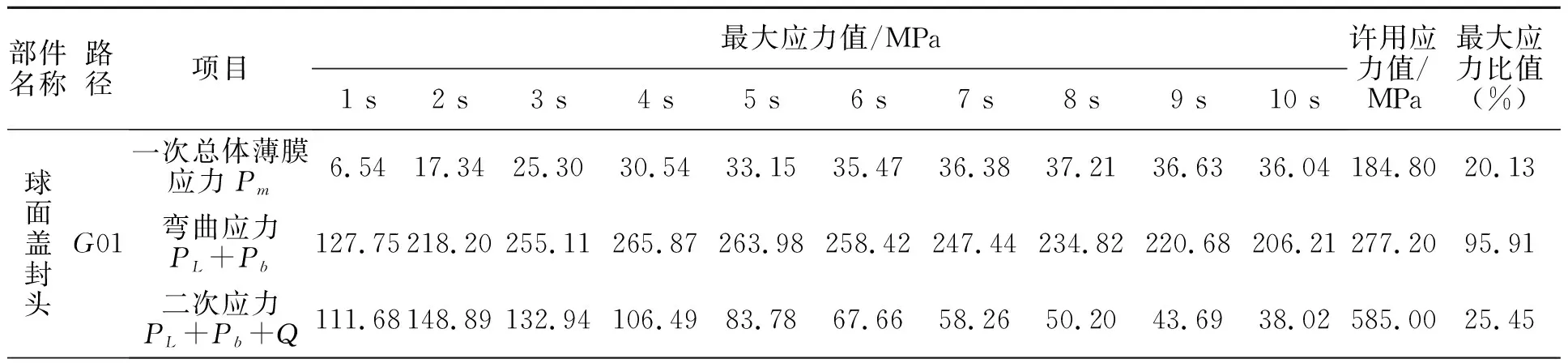
表7 设备闸门应力分类评定结果

(续表7)

3.2 结构耦合热应力密封影响分析

设备闸门整体受非对称载荷，选取变形量最大时刻的最大变形截面进行分析[18-20]。球面盖与下法兰呈分离的趋势，密封面截面发生明显的扭转。图12为该截面处法兰密封面形变示意，表8为该截面内外密封面上下表面位移时程表。在第9 s时，内密封面最大分离值为0.4 mm，外密封面最大分离值为0.21 mm，第10 s变化趋于稳定。

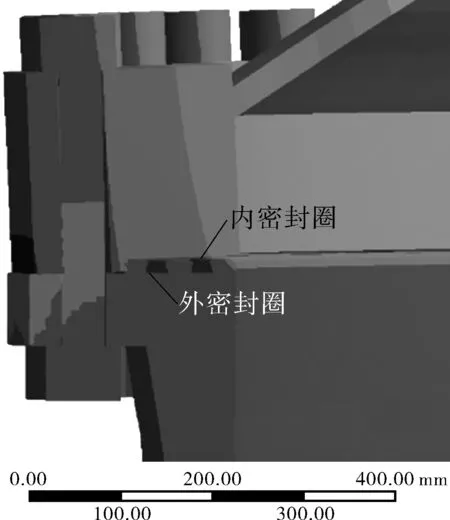
图12 法兰密封面形变示意

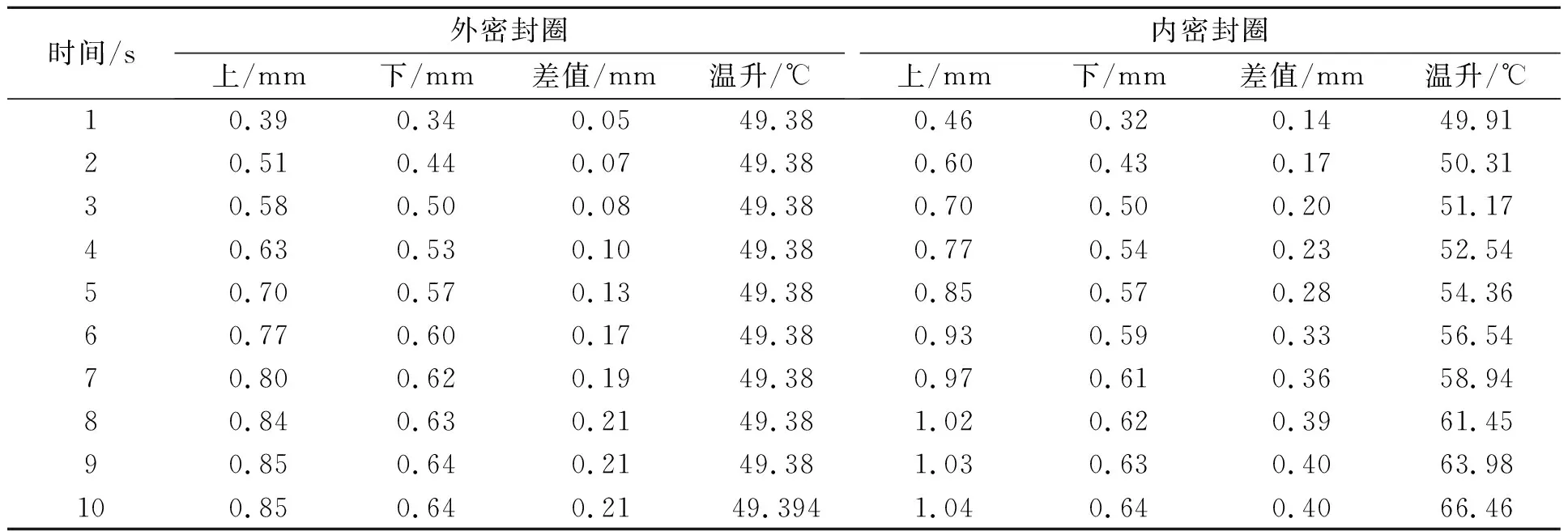
表8 内外密封面上下表面位移变化

在考虑瞬态热应力的情况下，内密封面存在约17 ℃的升温，而且密封面分离值较大，密封性能下降，外密封圈升温较低，密封面分离值较小，密封性能影响较小。因此，进行设备闸门密封性试验时，应根据计算的最危险结果增加升温状态下密封圈试验。

4 结论

本文计算浮动堆设备闸门正常运行工况下的热稳态温度场，并开展事故工况前10 s时刻的瞬态热应力、热应力最大值的变化趋势以及整体结构和主螺栓上的应力状态研究，得到接近真实的模拟结构工作状态。

(1)采用瞬态热固耦合方法计算可以较为准确地分析设备闸门各部件最大von Mises应力、完全应力、二次应力极值发生时刻，更准确地发现设计薄弱环节，并予以改进。

(2)在10 s内，设备闸门温度场由内表面至外表面呈现较为陡峭的梯度分布，特别是在内表面区域温度变化最大。可见在安全壳内突然升温，热量不能快速传递至外表面，形成热能在设备闸门内表面堆积的情况。计算结果显示，设备闸门内表面弯曲应力、二次应力受温度载荷变化显著。

(3)在考虑瞬态热应力的情况下，在第9 s时，内密封面存在约17 ℃的升温，而且密封面分离值约为0.4 mm，初步确定可能发生密封失效时的状态，为改进密封性试验提供数据支撑。

(4)本文采用等效静力的方法来处理冲击问题，取值也相对保守，但在工程实际中，船用核动力装置的冲击由船舶撞击、直升机坠落等外部事件引起，还需开展冲击响应分析，以便更为精确分析设备闸门的安全性。