胀接工艺和片距对金属复合管换热器接触热阻影响的数值研究

邓 君，张 华

(1.武汉科技大学 机械自动化学院，武汉 430081；2.武汉科技大学 冶金装备及其控制教育部重点实验室，武汉 430081；3.武汉科技大学 机械传动与制造工程湖北省重点实验室，武汉 430081；4.武汉科技大学 绿色制造工程研究院，武汉430081;5.武汉理工大学 船舶动力工程技术交通运输行业重点实验室，武汉 430070)

0 引言

金属复合管换热器是一种采用机械胀接成型、液压成型、热轧成型、爆炸成型等基于金属变形成型的连接工艺制造的换热设备[1]。由于金属复合管具有工作适应性好、制造成本低、便于工业化大规模生产的特点，广泛应用于各类换热场合[2]。

胀接工艺是制造金属复合管常用的工艺方法，胀接工艺的不同会影响金属复合管换热器的可靠性。王立辉等[3]对管子管板的胀接工艺进行了改进，发现改造方案可以提高工艺可靠性。潘秀娟等[4]对蒸汽发生器管头的胀接工艺进行了探讨，发现不同工艺对于提高蒸汽发生器的安全性有很大帮助。武玉洁等[5]对超级双相钢换热器的胀接工艺进行了试验研究，得到了满足胀管率下的胀管压力和胀接时间，并提出以此作为胀接过程的关键质量控制点。张泉达等[6]对铜管与翅片气压胀接工艺进行了试验和模拟研究，发现胀紧度随着铜管与翅片间过盈配合压力值的增大而增大。

胀接时，金属复合管在胀接力的作用下内圈壁和外圈壁同时膨胀，内圈壁发生塑性变形，外圈壁发生弹性变形。当胀接力消失后，内圈壁的塑性变形不会消失，外圈壁的弹性变形会回复，内外圈壁在回复的弹性变形力下结合在一起。原本内外圈壁间存在间隙，内外圈壁仅仅因为回复的变形力结合在一起，间隙不会完全消失，传热过程中也必然存在接触热阻。接触热阻是影响金属复合管换热器换热能力的重要问题，国内外学者[7-10]对该问题的研究均发现，接触热阻对金属复合管换热器的负面影响显著，并且具有一定的不确定性。现阶段，国内外学者们发现，通过试验能够有效地分析出接触热阻的试验关联式，用于指导换热器的设计和研究工作。如马其良等[11]对碳钢-铝翅片的接触热阻进行试验研究，拟合出对换热器设计和运行具有指导意义的试验关联式；张凡等[12]对4种相同加工工艺、不同材料的金属复合管的接触热阻进行了研究，拟合出试验准则式；TALER等[13]提供了一套基于试验和CFD模拟的修正方法，并用该方法研究了空气侧换热的情况等。试验拟合研究为研究内外管壁间接触热阻问题提供了参考。

对于金属复合管换热器来说，较小的片距意味着同等换热器体积下，具有更轻的质量、更高的翅片换热面积和更高的换热密度。然而在工业生产中，较小片距的翅片因为制造工艺和制造成本方面的限制，只能采用胀接成型工艺对该类型的换热器进行加工。不同于焊接成型及铸造成型工艺，胀接成型的金属复合管换热器在传热过程中必然存在接触热阻削弱换热器的传热效果[14-15]。因此，本文着眼于内外壁间的接触热阻问题，结合试验及数值模拟方法，介绍一种适用于工程上的金属复合管换热器平均接触热阻的近似计算方法，针对船用柴油机空冷器常用的两种片距(2.0，2.2 mm)的翅片，研究两种不同胀接工艺对接触热阻的影响。该接触热阻的研究方法能够部分解决接触热阻在传热过程中的不确定性问题，研究过程和研究结论可为后续金属复合管换热器接触热阻问题的研究提供帮助，为金属复合管换热器的生产工艺改进提供技术支持，同时可降低换热器的生产成本。

1 接触热阻计算原理及计算方法

1.1 计算原理

根据GB/T 2497—2008《船用柴油机增压空气冷却器》，当管内流体流速不变时，管外流体流速变化在设定范围内，则试验过程中金属复合管换热器总传热系数的表达式为：

Kexp=aReexpb

(1)

式中，Kexp为试验过程的总传热系数，W/(m2·K)；Reexp为试验设定的管外流体雷诺数；a,b为通过试验结果获得的待定系数。

同样，根据文献[9]，若假定金属复合管的平均接触热阻为Rtc，则模拟过程中金属复合管换热器总传热系数的表达式为：

Ksim=aResimb

(2)

式中，Ksim为模拟过程的总传热系数，W/(m2·K)；Resim为模拟设定的管外流体雷诺数;a,b为通过模拟结果获得的待定系数。

若假设存在一系列平均接触热阻Rtc1,Rtc2,……,Rtcn，则可以通过模拟获得一系列总传热系数表达式。

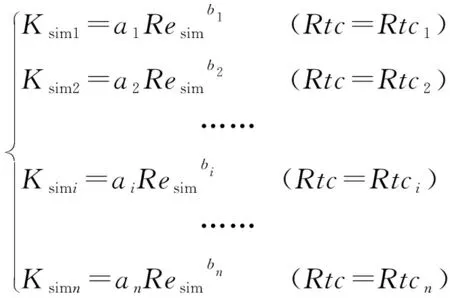
(3)

结合式(1)和式(3)，当Kexp=Ksim，且Reexp=Resim时，试验过程中的平均接触热阻Rtc与模拟过程中的接触热阻Rtci相等，且平均接触热阻的变化规律符合下式：

Rtc=Rct(Re)

(4)

式中，Rtc为接触热阻,(m2·K)/W；Re为K值相等时的管外流体雷诺数。

1.2 金属复合管换热器传热性能试验

1.2.1 试验台架

试验台架如图1所示。

(a)工作原理 (b)试验台架

图1(a)中，深色部分为空气流道，浅色部分为水流道；被测量金属复合管换热器位置见图1(b)。方管中含有隔热层以避免试验过程中的热散失。在空气流道中换热器前后位置分别布置4个温度传感器(方管的上下左右位置)，以避免大空间流道中流动的偏温效应对试验结果造成影响。

试验通过采集空气质量流量Qmair，空气侧入口、出口温度T1和T2，水侧入口、出口温度T3和T4的传感器数据，即可获得总传热系数K和管外雷诺数Re。具体计算公式如下：

(5)

(6)

其中：

Qh=Cpair(T1-T2)Qmair

(7)

(8)

式中，K为总传热系数，W/(m2·K)；Qh为换热总量，W；A为管外侧翅片面积(通过实际换热器计算得出)，m2；ΔTm为对数平均温差，K；ρ为密度，kg/m3；v为流速，m/s；γ为黏度，Pa·s；d为水力直径，m，d=(4Ad)/Ld=2Ph(其中，Ad为湿周面积，m2；Ld为湿周周长，m)；Qmair为空气质量流量，kg/s；Aflow为流通面积，m2；Ph为片距，m；Cpair为空气比热，J/(kg·K)；T1，T2为空气侧入口、出口温度，K；T3，T4为水侧入口、出口温度，K。

1.2.2 试验工况

在试验过程中，空气侧入口温度恒定为373.15 K(100 ℃)，空气侧雷诺数Re测量点设为2 000，3 000，4 000，5 000，6 000。水侧入口温度恒定为303.15 K(30 ℃)，水侧流速恒定为1 m/s。每个测量点测量2次，采用最小二乘法拟合式(1)，以获得试验过程总传热系数特性。

1.2.3 测试金属复合管翅片

由于本文主要研究胀接工艺和片距对金属复合管换热器的影响，特设置两种片距翅片及两种不同胀接工艺进行相关研究工作，具体如图2所示。

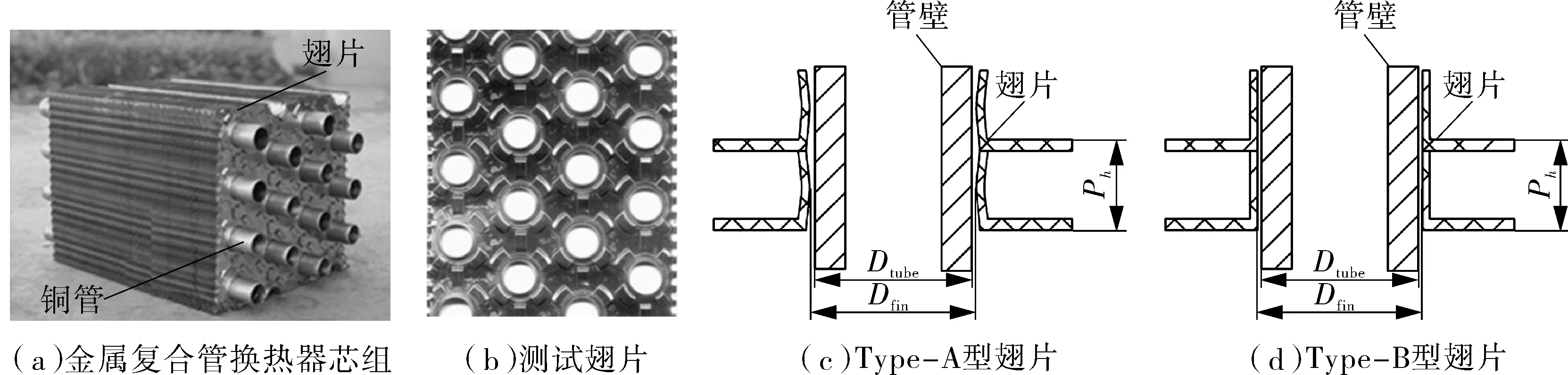
图2 测试金属复合管翅片实物及制作工艺、片距设定示意

Type-A型(见图2(c))为其中一种胀接工艺，Type-A型翅片采用非精密冲压模具制造，并且没有通过机械加工方法对该非平整管壁进行修饰，冲压后的翅片特点为非平整的翅片，翅片和管壁的贴合不紧密。Type-B型(见图2(d))为Type-A型的改进型，采用精密冲压模具制造，冲压后的翅片为平整的翅片，与管壁贴合较好。两种胀接工艺均将原Dtube=15 mm的管外径扩展成Dfin=15.4 mm的管外径，以此体现不同胀接工艺对接触热阻的影响。

两种不同片距是指Ph=2.0 mm和Ph=2.2 mm两种，原始片厚度均为0.12 mm，以此体现不同片距对接触热阻的影响。翅片的具体尺寸见图3。其中，图3(a)为根据实物建模的整体模型图，图3(b)为模型中具体翅片尺寸，图3(c)为图3(a)中局部细节N部分的尺寸，图3(d)为图3(b)中局部细节M部分的尺寸。

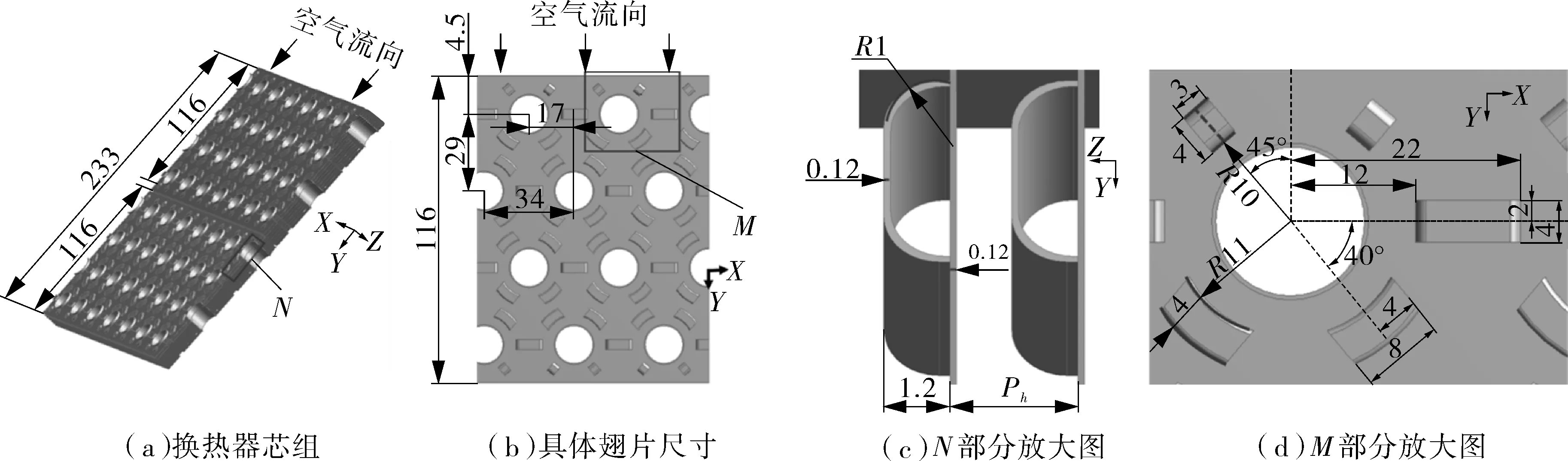
图3 翅片结构及寸示意

由图2,3可以看出，翅片的主要区别在于不同片距和不同胀接工艺。

1.3 金属复合管换热器性能模拟

1.3.1 模型缩减

在进行金属复合管换热器模拟时，计算规模太大，需要根据换热器的流动与尺寸关系对金属复合管换热器的计算模型进行缩减。缩减过程如图4所示，缩减后的模型如图5所示。其中，图4(a)为图1中空气流道和水流道的整体模型，图4(b)为图4(a)中被分割区域1，图5为图4(b)中被分割区域2，即被缩减后的计算模型域。

图4 模拟计算域分割示意

图5(a)为简化后的模型及其边界，图5(b)为图5(a)中Y轴视角，图5(c)为翅片和管模型，图5(d)为图5(c)中Y轴视角。空气绕圆管流动，若将管外的流动按照圆管轴线位置空气来流方向的平面进行分割，管外流动的两个部分流动状态与温度状态呈现出关于该平面的对称分布；水在管内流动，若将其流域按照空气侧平面进行分割，其流动状态和温度也呈现出关于该平面的对称分布，所以可以采用对称边界(Symmetry)模拟圆管内外的对称流动和温度情况，分割位置如图5(b)中对称边界位置。

图5 计算模型及边界条件

在两个片距距离的翅片上下表面(图5(b)中周期性边界位置)，空气流动和温度分布呈现出周期性分布，即流出上表面的流体流动状态和温度分布与流入下表面的流体流动状态和温度分布一致，采用周期性边界模拟其流动状态和温度情况。为了便于划分网格，选取1/4Ph的位置作为整个模型的周期性边界分割面，如图5(d)所示。

模拟过程中，由于不用考虑热散失效应，空气域入口段(从空气入口到翅片的长度)及出口段(从翅片到空气出口)的长度足够，测量结果与进出口位置无关；水流域，可以通过圆管内流动经验公式获得湍流状态数据，消除模拟过程与试验过程的误差。

整个翅片长度233 mm，由2个116 mm的翅片和1 mm的中间间隙组成，翅片宽度17 mm，水侧管内径14.2 mm，具体如图5(c)(d)所示。

1.3.2 边界条件和物性参数设置

试验过程中，假定空气和水的物性参数保持不变，金属复合管和翅片材料为T2铜，模拟过程中的物性参数如表1所示。

表1 模拟过程中的物性参数

试验过程中，水入口温度303.15 K(30 ℃)，入口流速为1 m/s。所以模拟过程中，水入口采用速度入口边界，水出口采用压力出口边界，水入口和出口湍流强度为4.71%，入口和出口水力直径为14.2 mm，出口背压为0 Pa，入口温度为303.15 K(30 ℃)，具体加载位置如图5(a)所示。

试验过程中，空气侧雷诺数Re范围为2 000～6 000，入口温度373.15 K(100 ℃)。所以在模拟过程中，空气入口采用速度入口边界，空气出口采用压力出口边界，加载位置如图5(a)所示，具体数值设置见表2(表中Set 1～Set 6为设定的覆盖空气侧雷诺数范围的6个不同工况)。

表2 空气侧入口与出口边界条件设定

1.3.3 模拟过程接触热阻的设置

由于接触热阻存在于管壁和翅片之间，所以接触热阻的加载位置如图6所示。

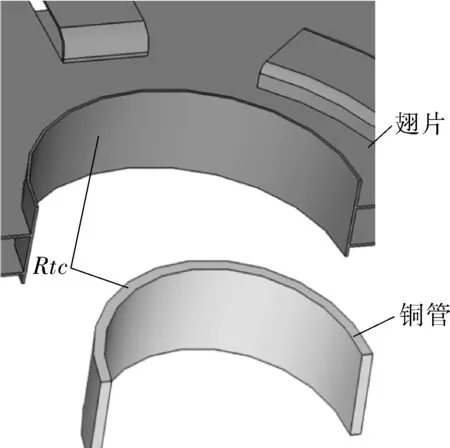
图6 接触热阻的加载位置

接触热阻在模拟时用金属锡的等效厚度表示，即:

(9)

式中，δe为锡的等效厚度,m;kSn为锡的导热系数,W/(m·K)。

1.3.4 网格划分及湍流模型

如图7所示，在划分网格时，固体材质网格均具有3层厚度，流体壁面附近均具有5层边界层网格，空气侧第1层网格厚度为0.01 mm，水侧第1层网格厚度为0.5 mm，计算过程采用k-e模型并结合Enhanced wall边界函数计算，计算过程均在流体计算软件FLUENT中完成。

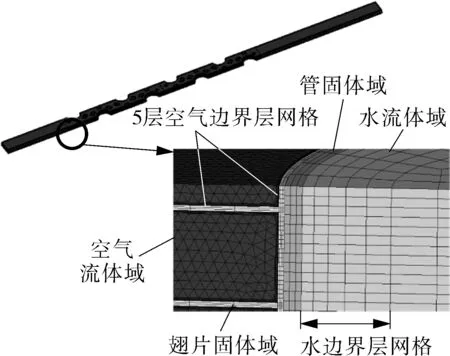
图7 模拟模型的局部网格模型

2 试验与模拟结果

2.1 金属复合管换热性能试验结果

经过试验，计算出4种复合管式换热器总传热系数如图8所示。图8中，Re代表空气侧变化的雷诺数，“2.0 mm Type-A”代表2.0 mm片距、Type-A型胀接工艺所制造的翅片。

图8 4种复合管式换热器总传热系数

从图8可看出，随着Re数值的变化(2 000～6 000)，2.0 mm Type-A型的K值变化范围为63～115 W/(m2·K)；2.0 mm Type-B型的K值变化范围为67～119 W/(m2·K)；2.2 mm Type-A型的K值变化范围57～96 W/(m2·K)；2.2 mm Type-B型的K值变化范围为61～103 W/(m2·K)。

从图8中还可以看出，胀接工艺对总传热系数K值具有一定影响。比较2.0 mm Type-A的数据和2.0 mm Type-B的数据可以看出，2.0 mm Type-B整体的传热系数K较大，并且随着Re的增加，2.0 mm Type-B的K值增加幅度也也比2.0 mm Type-A型的增加幅度大。该现象在2.2 mm Type-A和2.2 mm Type-B中也同样存在。

片距对总传热系数K值也具有一定的影响(见图8)。比较2.0 mm Type-A和2.2 mm Type-A可发现，2.0 mm Type-A型翅片整体K值均比2.2 mm Type-A型的大，随着Re从2 000增加到6 000，2.0 mm Type-A型翅片整体K值增幅也比2.2 mm Type-A型的增幅大。该现象在2.0 mm Type-B型和2.2 mm Type-B型中也同样存在。

从换热性能试验结果可以看出，胀接工艺和片距对金属复合管换热器的换热能力具有影响，Type-B型胀接工艺的换热能力大于Type-A型胀接工艺，片距2.0 mm的换热能力大于片距2.2 mm的换热能力。

2.2 金属复合管换热性能定接触热阻模拟结果

片距2.0 mm和片距2.2 mm定接触热阻模拟结果如图9,10所示。图中Re代表空气侧变化的雷诺数；K为模拟总传热系数；“RTC0.00055”代表接触热阻Rtc=0.000 55 (m2·K)/W时，对应的定接触热阻翅片的总传热系数曲线。

图9 片距2.0 mm翅片定接触热阻模拟结果

图10 片距2.2 mm翅片定接触热阻模拟结果

从图9中可以看出，当Re的变化范围为2 000～6 000时，RTC0.00023总传热系数从92 W/(m2·K)增加到114 W/(m2·K)，变化量为22 W/(m2·K)；RTC0.00055总传热系数从63 W/(m2·K)增加到66 W/(m2·K)，变化量为3 W/(m2·K)。图10中，片距2.2 mm翅片也具有类似的现象。

从定接触热阻模拟结果可以看出，接触热阻越大，当雷诺数Re相同时，总传热系数K值越小；接触热阻越大，总传热系数K值随着Re变动的增幅越小。

3 讨论

3.1 接触热阻的变化情况分析

将图8和图9进行叠加获得片距2.0 mm翅片模拟和试验结果比较图(见图11)，将图8和图10 进行叠加获得片距2.2 mm翅片模拟和试验结果比较图(见图12)。图11，12中，Re代表空气侧变化的雷诺数；K为总传热系数；“RTC 0.00055”代表接触热阻Rtc=0.000 55 (m2·K)/W时，对应的定接触热阻翅片的总传热系数模拟曲线；“2.0 mm TYPE-A”代表2.0 mm Type-A型翅片的总传热系数试验曲线。

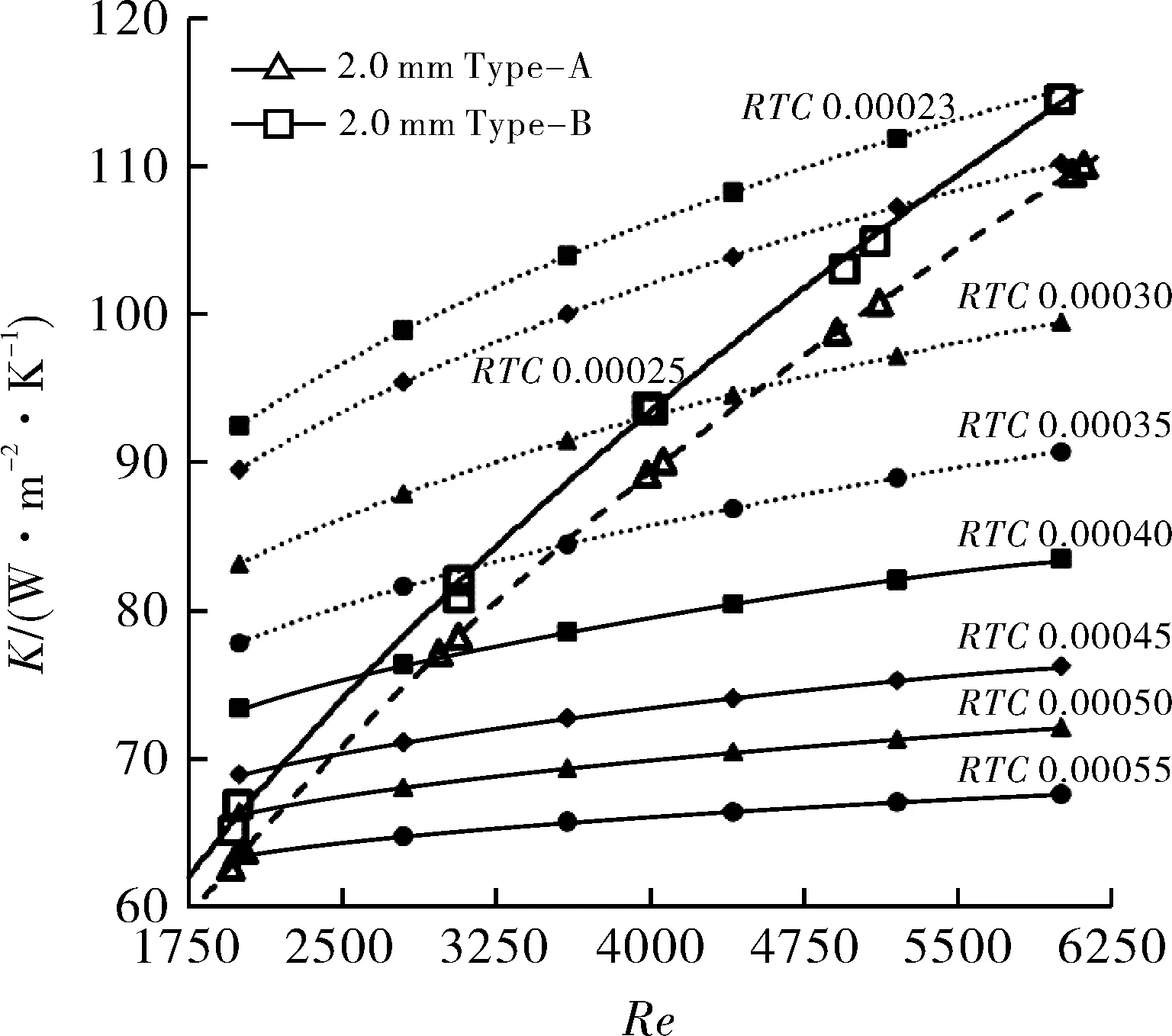
图11 片距2.0 mm翅片模拟和试验结果比较

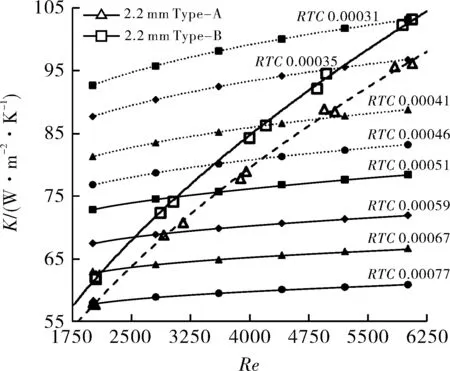
图12 片距2.2 mm翅片模拟和试验结果比较

从图11看出，Re=2 000时，2.0 mm Type-A型翅片的接触热阻约0.000 55 (m2·K)/W，2.0 mm Type-B型翅片的接触热阻约为0.000 50 (m2·K)/W；Re=6 000时，2.0 mm Type-A型翅片的接触热阻约为0.000 25 (m2·K)/W，2.0 mm Type-B型翅片的接触热阻约为0.000 23(m2·K)/W。

从图12看出，Re=2 000时，2.2 mm Type-A型翅片的接触热阻约0.000 77 (m2·K)/W，2.2 mm Type-B型翅片的接触热阻约0.000 67 (m2·K)/W；Re=6 000时，2.2 mm Type-A型翅片的接触热阻约0.000 35(m2·K)/W，2.2 mm Type-B型翅片的接触热阻约为0.000 31 (m2·K)/W。

从图11，12中可以看出，随着雷诺数Re的增加，翅片的接触热阻开始减小；Type-B型翅片的接触热阻整体上小于Type-A型翅片。由此可见，金属复合管换热器的接触热阻会随着换热工况的变化而变化；并且，片距、胀接工艺的不同会造成变化规律的不同。

3.2 接触热阻变化规律的数值分析

通过图11，12中试验K值曲线和定接触热阻模拟K值曲线，可以找出一系列的(Re,Rtc)点，这些点可以通过多项式展开的方法获得单一翅片接触热阻随着空气侧雷诺数变化的情况。

从图11，12中获得的4种翅片试验和模拟结果曲线交点(Re，Rtc)见表3,4。根据表3，4，片距2.0 mm翅片和片距2.2 mm翅片的接触热阻变化规律如图13所示。图13中，Re为空气侧雷诺数;Rtc为实际平均接触热阻。

表3 片距2.0 mm翅片在图11中的交点

表4 片距2.2 mm翅片在图12中的交点

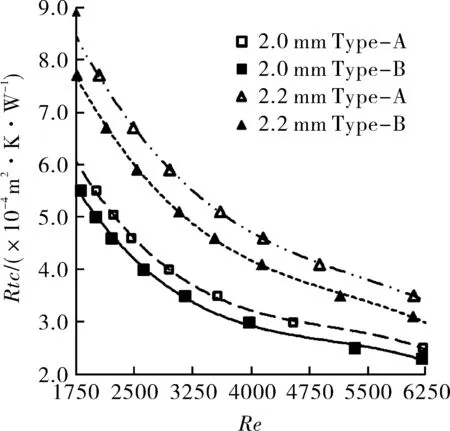
图13 4种翅片接触热阻Rtc变化曲线

从图13可以看出，Re的变化范围为2 000～4 000时，2.0 mm Type-A型翅片接触热阻的变化范围为0.000 545～0.000 324 (m2·K)/W，幅值为-0.000 221(m2·K)/W；2.0 mm Type-B型翅片接触热阻变化范围0.000 493～0.000 301(m2·K)/W，幅值为-0.000 192 (m2·K)/W；2.2 mm Type-A型翅片接触热阻的变化范围为0.000 776～0.000 466 (m2·K)/W，幅值为-0.000 310 (m2·K)/W；2.2 mm Type-B型翅片接触热阻的变化范围为0.000 680～0.000 423 (m2·K)/W，幅值为-0.000 257 (m2·K)/W。当Re的变化范围为4 000～6 000时，2.0 mm Type-A型翅片接触热阻变化范围0.000 324～0.000 270 (m2·K)/W，幅值-0.000 054 (m2·K)/W；2.0 mm Type-B型翅片接触热阻的变化范围为0.000 301～0.000 241 (m2·K)/W，幅值为-0.000 060 (m2·K)/W；2.2 mm Type-A型翅片接触热阻的变化范围为0.000 466～0.000 348 (m2·K)/W，幅值为-0.000 118 (m2·K)/W；2.2 mm Type-B型翅片接触热阻的变化范围为0.000 423～0.000 321 (m2·K)/W，幅值为-0.000 102 (m2·K)/W。

综上所述，片距2.0mm翅片的接触热阻小于片距2.2 mm翅片；Type-B型胀接工艺翅片接触热阻小于Type-A型胀接工艺翅片；随着雷诺数Re的增加，4种翅片接触热阻均下降，当Re范围为2 000～4 000时，接触热阻的数值及下降幅值均较大，当Re范围为4 000～6 000时，相对于Re范围为2 000～4 000，接触热阻的数值及下降幅值均较小。

根据表3，4，接触热阻特性的拟合表达式见公式(10)～(13)。

2.0 mm Type-A型：

Rtc=-6.5251×10-15Re3+9.3753×10-11Re2

-5.0585×10-7Re+1.1759×10-3

(10)

2.0 mm Type-B型：

Rtc=-7.4274×10-15Re3+1.0958×10-11Re2-5.6171×10-7Re+1.2905×10-3

(11)

2.2 mm Type-A型：

Rtc=-6.2419×10-15Re3+9.7884×10-11Re2-5.5642×10-7Re+1.4763×10-3

(12)

2.2 mm Type-B型：

Rtc=-5.4955×10-15Re3+8.9918×10-11Re2-5.3971×10-7Re+1.5429×10-3

(13)

3.3 管和翅片温度变化规律解析

本文通过研究管1位置基管和翅片管温度变化规律，验证接触热阻变化规律的正确性。管1位置如图14所示，平均温度结果如表5所示。

图14 管1位置示意

图14为图4(a)的Z轴视角图。由此可见，管1位置为最热空气和水热交换的位置，温度变化结果具有代表性。表5中的温度结果为基管及靠近基管附近翅片管的平均温度。

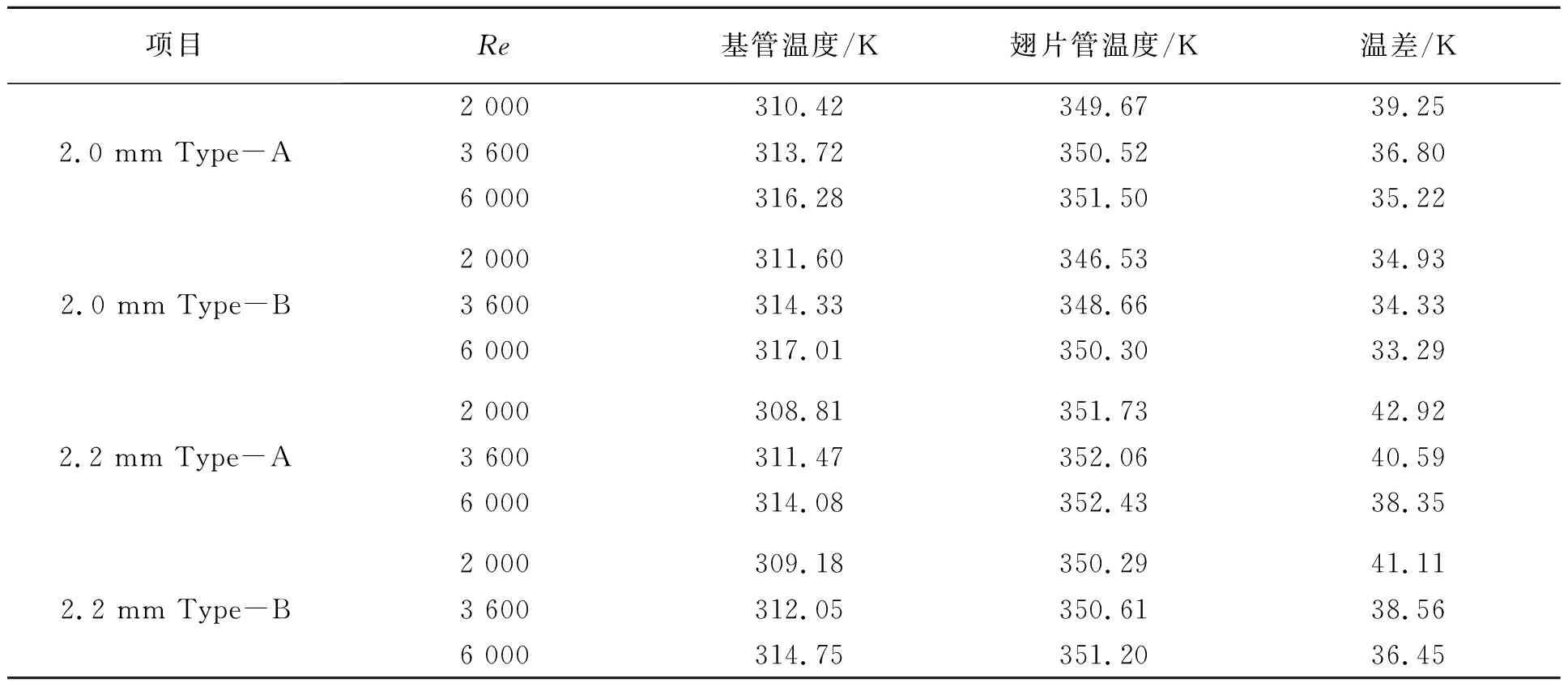
表5 基管和翅片管平均温度结果

结合表5和图13可以看出，接触热阻的变化规律与基管和翅片管的温度变化规律密切相关。随着雷诺数Re的增大，翅片管温度略微增加，基管温度显著增加，基管与翅片管间的温差减小，接触热阻下降；对于同片距翅片，Type-B型翅片管的接触热阻低于Type-A型，Type-B型基管温度略高于Type-A型。

造成接触热阻变化规律和翅片管温度变化规律密切相关的主要原因是传热过程中翅片管的温度变化。在整个试验过程中，管内流体流速和温度不变，所以管内换热系数不变，参考温度不变。当空气侧雷诺数上升时，换热密度增大，体现的后果就是基管温度上升。Type-B型初始接触热阻比Type-A型小，随着空气侧雷诺数增大，Type-B型基管温度及其上升幅度也均高于Type-A型。整个金属复合管的受力状态可以被视为同心环状受力状态，内管温度上升幅度高于外管，由于热膨胀作用，内管向外膨胀，基管和翅片管间的接触压力增加，接触热阻也会进一步减小。减小的接触热阻会进一步增加换热密度，造成翅片温度降低。

由此可见，2.0 mm Type-A型、2.0 mm Type-B型、2.2 mm Type-A型和2.2 mm Type-B型翅片接触热阻变化的主要原因是基管温度上升。相同换热工况下，具有更低接触热阻金属复合管的特征是具有更高的基管温度。

4 结语

结合试验与模拟方法，介绍了一种适用于工程使用的金属复合管接触热阻计算方法，并用该方法对两种不同胀接工艺下片距2.0 mm和片距2.2 mm翅片的接触热阻展开研究，得到4种翅片的传热特性；分析了接触热阻对翅片换热的影响情况、片距和胀接工艺对接触热阻的影响情况；得到这4种翅片接触热阻变化的数值规律。

通过上述研究工作，可以得出如下结论。

(1)片距2.0 mm翅片的换热能力优于片距2.2 mm翅片，胀接工艺Type-B型翅片的换热能力优于Type-A型翅片；

(2)片距2.0 mm翅片的接触热阻小于片距2.2 mm翅片，Type-B型胀接工艺翅片接触热阻小于Type-A型胀接工艺翅片；

(3)随着雷诺数Re的增加，4种翅片接触热阻均减小，当Re范围为2 000～4 000时，接触热阻的下降幅度较大且接触热阻较大；当Re范围为4 000～6 000时，接触热阻的下降幅度较小、接触热阻也较小。

(4)金属复合管接触热阻变化的具体表现为变化的基管和翅片管温度，较高的基管温度具有较低的接触热阻。

由此可见，Type-B型胀接工艺、2.0 mm片距以及高雷诺数(Re>4 000)均能直接减小接触热阻，从而提高金属复合管换热器的换热能力。在换热器强化传热设计过程中，应尽量使用平整后的翅片作为胀接工艺的基础，采用较小的片距和较大的换热负荷以尽量降低因为接触热阻而带来的换热能力损失，提高金属复合管换热器的传热能力。然而，较小的片距及高雷诺数均会增大金属复合管换热器的压降，降低换热过程的经济性，如何合理地权衡胀接工艺、片距和雷诺数这三者的关系，合理优化换热过程经济性是需要进行的后续工作。本文的研究方法能够部分解决接触热阻在传热过程中的不确定性问题，计算方法和研究结论可为研究后续金属复合管换热器接触热阻问题提供帮助。