稀疏激光扫描点的自主移动机器人地图创建

贾丙佳， 李平

(华侨大学 信息科学与工程学院， 福建 厦门 361021)

地图创建是移动机器人研究领域的核心及热点问题.如果没有精确的地图作为先验条件，机器人就无法自主执行一些任务，也无法确定自身相对于环境的位姿(位置和姿态角).因此，利用传感器感知周围环境信息，是移动机器人必须具备的一项基本功能[1-2].常用的传感器有声波传感器[3]、视觉传感器[4]和激光传感器[5]等.声波传感器具有发散性，测量距离越远，误差越大.视觉传感器对环境和处理速度的要求较高.相较而言，激光传感器在精度、速度和稳定性方面都具有更好的性能[6].

在利用激光雷达创建环境地图方面，国内外众多学者已进行大量的研究[7-9].其中，应用最为广泛的是迭代最近点(ICP)算法[10].ICP算法可以对不同时刻传感器获取的二维或三维环境深度信息进行配准，寻求一组旋转和平移参数，使配准后的两帧深度数据达到最大程度的重叠[11-12]，同时，经计算可得不同时刻传感器在环境中的位姿.然而，传统ICP算法在实际应用中存在收敛速度慢、对给定初值敏感、易陷入局部最优、相邻两次扫描点不存在单映射关系等缺陷[13-15].为解决这些问题，文献[16]采用基于改进k-D树的方法，提高对应点查找速度.文献[17-19]采用基于点-直线匹配(PLICP)方法和几何方法解决扫描点集不符合单映射的问题，筛选出对应点对，并减少点对的搜索次数.文献[20]提出一种基于判断点云领域法向量夹角的自动配准算法.基于此，针对激光雷达相邻扫描点集之间不存在一对一单映射关系的问题，本文提出一种稀疏扫描点的对应点对搜索算法.

1 二维点集粗配准

1.1 扫描点的采集

通过传感器采集环境的深度数据，采用Neato XV-11型激光雷达(图1)，其有效测量范围为0.15～4.00 m，每旋转360°会扫描产生360个距离数据，即1°对应1个距离数据，并返回1组极坐标表示的二维扫描点集O={(θi,ρi)|i=0,…,n}.其中：θi为激光雷达自身扫描第i度的角度信息；ρi为第i个角度上的距离；n为扫描点的个数.

将扫描点集数据从极坐标系转换到直角坐标系，有

xi=ρicosθi,yi=ρisinθi，

(1)

并用集合P={(xi,yi)|i=1,…,n}表示.

在数据采集过程中，通常间隔一定的时间或移动机器人位姿改变一定的阈值时，进行一次数据采集.由于运行中的机器人位姿不会发生突变,且具有连续性，故采集到的相邻时刻扫描数据点集具有明显的对应关系.激光扫描简图，如图2所示.图2中：红色点表示机器人在M0处的激光扫描点；蓝色点表示机器人在M1处的激光扫描点；车载红点和蓝点表示激光雷达的安装位置；点之间的连线表示激光扫描时的射线，图中仅画出一部分；R表示机器人；黑色边框表示墙壁；A～C表示相同位置不同时刻激光点的分布.由于相邻两个时刻机器人的位姿无较大变化，故相邻两个时刻的数据集将大部分重叠.

图1 激光雷达实物图 图2 激光扫描简图 Fig.1 Physical picture of laser lidar Fig.2 Laser scanning diagram

1.2 问题的分析

自主移动机器人创建环境地图时，在环境中不断地移动，一方面，有新的环境进入激光雷达的可测范围，也有当前环境远离可测范围，导致相邻两个时刻激光雷达产生的两帧点集数据不能完全重叠，而自主移动机器人连续、不突变的的运动特点使两帧数据只有小部分无法重叠，不重叠的数据代表新地图的特征，由此创建出增量式的地图；另一方面，即使机器人不移动，激光雷达的测量噪声也会导致两帧数据不完全重叠，这种测量噪声无法准确排除，特别是在复杂的环境中，更无法排除这种噪点是测量噪声还是环境特征.

在激光扫描简图中，机器人两次扫描环境时的姿态角没有变化，仅改变位置.然而，在实际创建地图过程中，机器人的位置和姿态角均发生变化，此时，以激光雷达为坐标系的扫描点集数据就会发生错位，进一步使两帧扫描点集重叠部分变少.为了使ICP算法具有最佳的初值，快速收敛到正确的结果，前期的粗匹配尤为重要.

1.3 方向和位置的配准

为了使相邻时刻激光雷达扫描数据尽可能最大程度地重叠，对扫描数据进行粗配准.采用方向柱状图匹配法[21]，对每一帧扫描点集计算连续两个扫描点构成直线的角度，得到两帧扫描点集的角度柱状图，再经互相关得到两帧扫描点集的相对角度对应关系，互相关函数为

(2)

其离散形式为

(3)

式(2)，(3)中：h1，h2分别为相邻时刻的扫描点集；X,Y，Z，I,J均为方程变量.

由于激光雷达通过不同位姿对同一环境扫描得到的数据方向柱状图仅相差一定的角度，利用互相关函数搜索到的最大值即两次扫描数据的相对角度差Δθ.方向配准后，进行位置配准.分别计算两帧扫描点集数据的重心，计算重心间的距离，可得x轴和y轴的距离差，即位置配准在x轴和y轴方向移动的距离.

通过上述方向和位置配准处理后，两帧数据在主方向和重心上都能大致重合，这将有利于后续准确建立对应点对搜索机制，以及确定扫描点间一对一单映射关系.需要注意的是，在进行粗配准时，先要进行方向配准，只有方向配准到一致时，位置配准才能更加准确.

2 二维点集精配准

在不采用编码器信息的情况下，仅利用激光雷达采集的扫描点集数据进行环境地图的创建.由于自主移动机器人在运行过程中的位姿不会发生突变，相邻时刻两帧扫描点集数据具有明显的对应关系，故采用ICP算法计算激光雷达在相邻两个时刻的位姿变化量.

2.1 ICP算法概述

ICP算法[10]是基于最小二乘优化思想的配准算法，具有精度高、编程实现简易等优点.

将激光雷达当前扫描点集变换到与参考扫描点集相同的坐标系下，有

Q1:n=R·P1:n+T.

(4)

式(4)中：Q1:n，P1:n分别为参考扫描点集与当前扫描点集，两个点集数据数量相等；R为3×3的旋转矩阵；T为3×1的平移向量.

ICP算法有以下6个步骤.

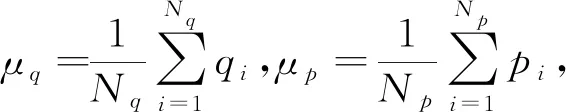
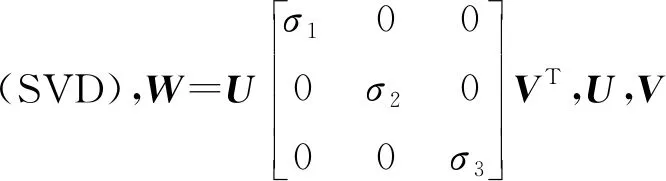
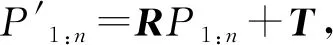
ICP算法的核心是最小化目标函数，即

(5)

经迭代计算出正确的配准结果.

2.2 问题分析

ICP算法的实现原理，必须满足以下2个假设.

1) 参考扫描点集和待配准的当前扫描点集的个数完全相同，对应点对需完全满足一对一单映射对应关系.

2) 选取合适的R,T作为迭代初始值，使最终目标函数最小，迭代次数最少.

然而，ICP算法的假设过于理想化，这两个假设在实际应用中很难得到满足.

首先，自主移动机器人搭载激光雷达在环境中移动，探测到的新环境造成相邻时刻激光扫描数据不完全重合(图2)，则A～C处会出现以下3种情况：1) 情况1，前一次的扫描点集多于后一次；2) 情况2，前一次的扫描点集和后一次相等;3) 情况3，前一次的扫描点集少于后一次.如果把前一次的扫描点集当成参考扫描点集，则相对于前一次的扫描点集，后一次的点集会出现一对多、一对一和多对一的情况，情况2的两帧点集则具备一对一的单映射对应关系.

对应点示意图，如图3所示.图3中：红色点为参考扫描点；蓝色点为当前扫描点.将蓝色点配准到红色点位置，在A～C处不存在一对一单映射对应关系，而其他位置的多数点存在明显的对应关系.

其次，相邻时刻机器人的位姿变化并不一致，迭代初值必须随之进行适当地更改.受上述因素影响，直接使用ICP算法进行配准，结果会存在较大误差.

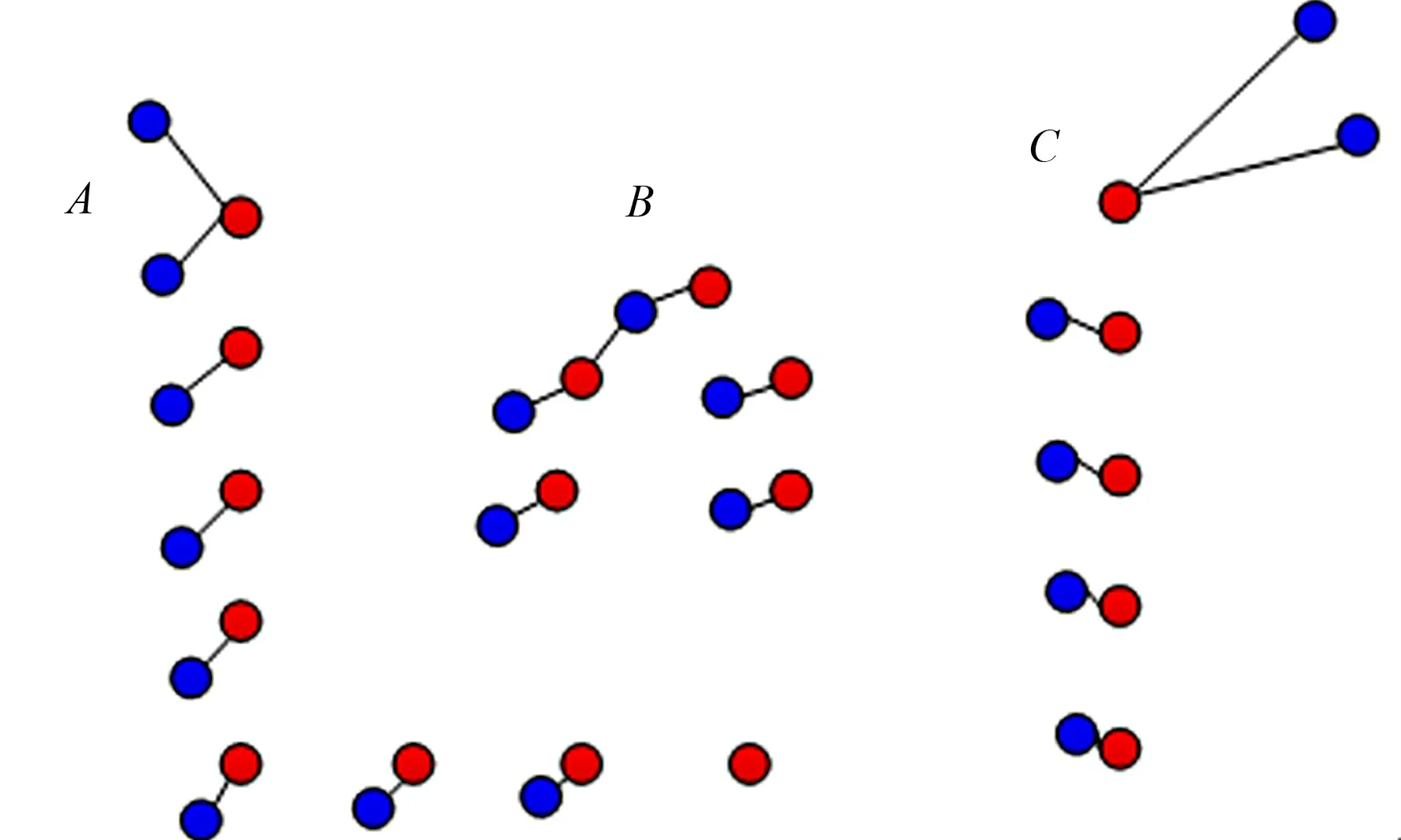
图3 对应点示意图Fig.3 Schematic diagram of corresponding points

因此，两帧扫描点集数据对应点对的查找及迭代初值的设置是实现ICP精配准的关键，在此基础上才能创建较为精确的地图.

2.3 对应点对搜索机制

首先，不满足一对一单映射对应关系的数据点可以忽略，即从当前扫描点集中剔除.

然后，重建点集，使最终配准的两帧扫描点集具有一对一单映射对应关系.由于在精配准之前，已进行了粗配准，但其只能减小扫描点集之间的错位，并不能在A，B处实现完全重叠.C处是小车在M1位置的环境扫描点(图2)，代表新的环境特征，而在M0处的扫描点集中并没有对应的点，因此，需要对M1处扫描得到的数据进行稀疏处理，具体有以下4个步骤.

步骤1根据两帧扫描点集，构建曼哈顿距离矩阵，第i个当前扫描点和第j个参考扫描点之间的曼哈顿距离d(i,j)为

d(i,j)=|xi-xj|+|yi-yj|.

(6)

式(6)中：xi，yi分别为第i个点的横、纵坐标;xj,yj分别为第j个点的横、纵坐标；i，j≤360.

矩阵中的每个元素表示Q1:n点集中的每一个点相对于P1:n点集中每一个点的距离，如图4所示.图4中：水平方向排列的是i个当前扫描点坐标；垂直方向排列的是j个参考扫描点坐标.

步骤3构建3×1的动态搜索窗口，按照初始最小值在矩阵中的索引，进行后续迭代搜索，需满足

(7)

图4 曼哈顿距离矩阵示意图 图5 搜索路径示意图Fig.4 Schematic diagram of Manhattan distance matrix Fig.5 Schematic diagram of search path

步骤4重复步骤3，直至搜索完i列数据.

完成步骤1～4，可搜索出一条路径.迭代搜索过程中需要满足以下2个约束条件.

1) 连续性.相邻搜索点是连续的，即下一个搜索点必须是D(j-1,i+1),D(j,i+1)和D(j+1,i+1)这3点中的一点.

2) 单调性.垂直方向按照曼哈顿距离矩阵中数值递减的方向进行搜索，水平方向按照当前扫描点P1:n索引的排列顺序依次搜索.

对于节2.2描述的3种情况，其路径搜索示意图，如图6所示.图6中：左侧为搜索路径原理分析图；右侧为实验结果图；左侧红色虚线框表示一次搜索过程需搜索的3个点；右侧红色实线框是搜索到的距离最小值.由于采用科学计数法，搜索路径中的距离最小值并不都为零.

(a) 一对多

(b) 一对一

(c) 多对一图6 路径搜索示意图Fig.6 Schematic diagram of path search

2.4 稀疏扫描点

搜索路径上的动态搜索窗口并没有过多地偏离上一次搜索到的最小距离值，即动态搜索窗口的索引值变化量在[0 1]范围内变化，且正常情况下的索引值变化量为Δi=1，Δj=1.在索引值变化量Δi，Δj不为1时，删除该索引值对应的当前扫描点和参考扫描点.此外，一方面，当索引值变化量较大时，点会被删除(图3)；另一方面，设置1个最小曼哈顿距离阈值D，当搜索到的最小值比D大时，这两种情况下同样删除该索引值对应的当前扫描点和参考扫描点，这些对应点视为无效对应点.

删除无效对应点后，重建当前扫描点集，可得到稀疏扫描点集.

2.5 点集精配准

采用ICP算法对稀疏扫描点集与参考扫描点集进行精配准，此时，待匹配的是过滤后的数据点，已排除一对多和多对一的情况，可获得较精确的ICP配准结果.经配准可得旋转矩阵和平移向量，应用式(4)对当前扫描点的原始点集数据进行变换操作，将当前扫描点匹配到参考扫描点坐标系中.然后，将配准前的当前扫描点作为参考扫描点，激光雷达下一时刻扫描得到的点集作为当前扫描点集，进行下一步配准，并将上一次配准结果作为该次配准的初值.计算获得该次配准结果并累加之前的配准结果，对当前扫描点集进行变换.依此类推，可创建出整个环境地图.地图创建流程图，如图7所示.

图7 地图创建流程图Fig.7 Flowchart of map creation

3 结果与分析

应用MATLAB仿真平台，在局部环境下，通过相邻两帧扫描点集验证文中方法的有效性.实验平台为Inert(R) Core(TM) i3-3220 CPU，3.30 GHz主频和4.00 GB内存的笔记本电脑，Windows 10操作系统.实验数据来自Neato XV-11型激光雷达，开发平台为微软Microsoft Visual Studio 2017，采用C#编程语言编写激光雷达的数据解析代码和扫描点数据配准代码.

相邻两帧扫描点集配准结果，如图8所示.图8中：红色点为参考扫描点；蓝色点为当前扫描点.实验目的是将蓝色点配准到红色点的位置.由图8可知：在一定距离阈值内，存在部分无法建立对应关系的数据点；剔除无效点后，红色和蓝色数据已最大程度地重叠.将当前扫描点作为参考扫描点，对下一帧点集数据进行配准，进而将两两点集数据进行同样的处理，直至停止数据采集，即可建立环境地图.

(a) 激光扫描原始数据 (b) 文中方法匹配结果图8 相邻两帧扫描点集配准结果Fig.8 Matching results of two adjacent scan point sets

表1 不同方法的配准结果Tab.1 Registration results of different methods

为验证文中算法配准结果的准确性，将其与ICP算法、文献[16]方法、文献[17]方法、文献[20]方法进行对比.不同方法的配准结果，如表1所示.表1中：e为配准误差；C为迭代次数.

由表1可知:在相同的扫描点集下，ICP算法的配准误差较大；文献[16]方法采用k-D树加速对应点的查找，迭代次数减少，但配准误差较大；文献[17]方法采用点-直线的匹配方法，迭代次数和配准误差均有降低；文献[20]方法虽然滤除了测量噪声点，但依然存在相邻两帧扫描点集无效对应的点；文中方法在前处理过程中将无效对应点剔除，其配准误差和迭代次数均优于其他方法，可提高地图创建的准确性.

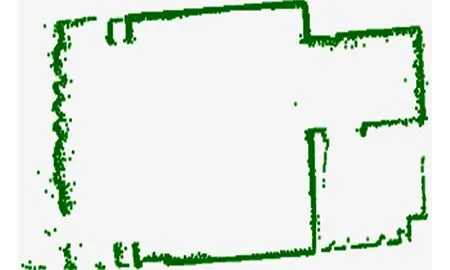
图9 实际环境配准图Fig.9 Registration map of actual environment

在实际环境中，激光雷达多帧扫描数据两两匹配的结果，如图9所示.由图9可知：文中方法可以消除ICP算法因不满足一对一单映射对应关系而产生的数据错位问题.由此可知，实际环境中的配准结果验证了文中方法的有效性.

4 结束语

提出一种稀疏激光扫描点的自主移动机器人地图创建方法.在粗配准后，运用稀疏扫描点的对应点对搜索方法，对激光雷达环境扫描点集建立对应点对搜索机制，根据曼哈顿距离剔除无效对应点，在精配准时提高ICP算法的配准精度，减少搜索次数，建立环境地图.实验结果验证了文中方法的准确性和有效性.