基于时空预处理DS证据的同质传感器数据融合
朱 聪
(中铁二院工程集团有限责任公司,四川成都 610031)
0 引言
多个传感器监测一个对象,将多个传感器数据融合成一个值称为同质传感器数据融合。综合管廊作为现今保障城市运行的重要基础设施,其内部存在种类繁多、数量庞大的传感器群。为降低数据传输成本,提高数据精度,增加数据鲁棒性,近年来主要采用多传感器数据融合的方式处理传感器数据。
针对传感器的数据融合,国内外学者进行了深入的研究[1-9]。其中,代啟林等[1]以电化学气体传感器为研究对象,提出了基于线性神经网络的数据融合算法,解决了常规测量在较大测量范围的精密测量问题。徐建亮等[2]为消除传感器间可能存在的虚假或错误数据,提出了一种基于粒子滤波算法(PFA)的改进贝叶斯算法(IBA),提高了数据融合精度。左延红等[3]针对制造系统中检测节点环境与设备的的差异性,提出了基于分数阶微分的多传感器检测数据融合算法,提高了数据的可靠性。曹守启等[4]为解决水产运输过程中多传感器检测数据误差大的问题,提出了一种结合分批估计和自适应加权的数据融合算法,增强了数据稳定性。陈英等[5]根据数据多样性提出一种利用小波变换阈值去噪的多传感器融合算法,对信息的保留效果有较大提高。H. S. Zhai[6]提出了基于无损Kalman滤波及小波变换的多传感器数据融合方法,对数据先分解后重构,提高了融合数据的抗干扰性及准确性。K. Kim等[7]以韩国的高铁为研究主体,提出了基于Kalman滤波的非完整控制数据融合算法,有效解决了列车通过隧道时RFID部署间距、定位的不准确性及GDPS错误等问题。璩晶磊等[8]为提高数据融合精度,提出了基于模糊证据理论的多传感器融合算法,该方法无需历史数据,在单次测量中融合效果较好。潘啄金等[9]为减少数据传输量,提出结合了深度自编码的WSN融合算法,该方法有效提高了数据传输效率。
DS(dempster-shafer)方法认为多个传感器之间通常具有数据一致性,能够相互验证。如果某个传感器数据明显异于其他传感器,说明其他传感器不支持该异常传感器,该传感器的可信度低。基于上述思路,DS方法将每个传感器定义为目标传感器,对于每个目标传感器,将所有传感器作为支撑该目标传感器的证据,通过这些证据计算目标传感器的可信度。根据可信度对所有目标传感器加权平均获得最终融合值。现有DS方法主要是针对单传感器的误差或多传感器融合的精度进行研究。但都未考量各传感器的时空特征,导致数据的可信度较低或完全丢失。针对DS方法中的噪声和异常数据,以及容易丢失数据特征的问题,提出一种基于时空预处理的DS证据方法(spatio-temporal DS,ST-DS),用于多传感器数据融合。本文设计了一种时空预处理机制,根据数据的空间和历史变化规律剔除异常和噪声,并寻找数据特征区域。同时结合DS方法,根据数据空间分布和特征区域位置计算证据的信任分配。首先对传统DS证据理论进行改进,在此基础上引入时空预处理,对争议点数据进行可信度判断,最后通过融合证据获得同质传感器的融合数据。本文算法的结构框图如图1所示。将传感器所探测到的数据进行时空预处理;进行ST-DS数据融合;获得最终融合值。

图1 本文算法流程
采用本方法对综合管廊中的甲烷浓度传感器数据进行融合,实验结果表明在发生甲烷泄漏的情况下,本文融合数值明显高于其他方法,并在甲烷未发生泄漏时基本保持一致,认为本文方法有较高的有效性及实用性。
1 多传感器数据时空预处理
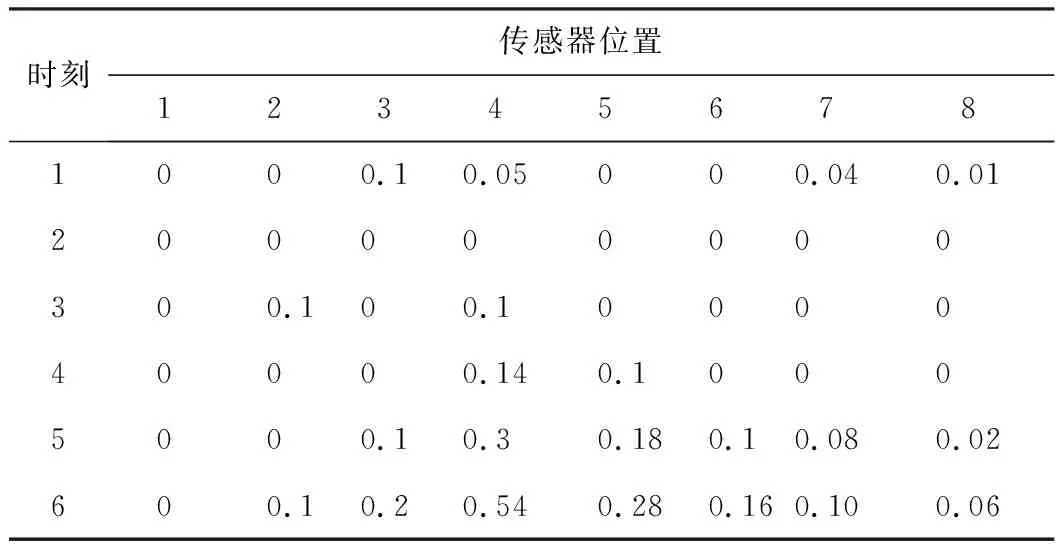
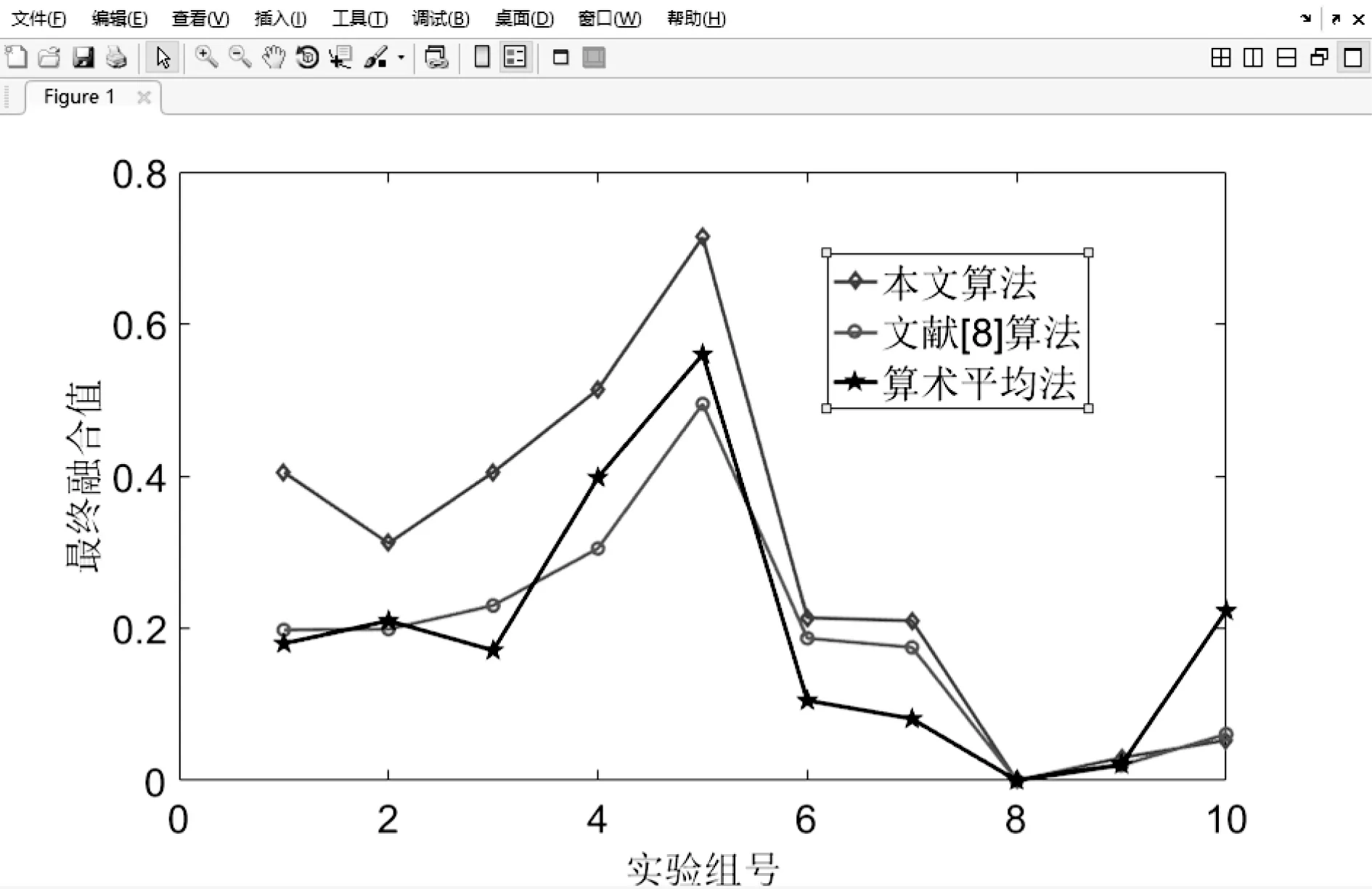
本文以综合管廊一个防火分区中布置的甲烷传感器为研究对象,沿防火分区布置多个甲烷气体浓度传感器采集数据。多个同质传感器按线性布置,位置s处的传感器数据为J(s),s=1~S,S为传感器总数。引入时间信息后,s处,t时刻的传感器数据为J(t,s),t=1~T,T为最新时刻。对于任意t (1) 设计3个指标用于检测噪声和异常数据:空间均值、空间一致性、时间一致性。采用区域熵寻找特征区域,例如数据出现明显变化,或出现峰值的区域。 1.1.1 空间均值 最新时刻T时,所有位置处数据的均值可表示为 (2) 目标时序N定义为时间变化的最新时序。 1.1.2 空间一致性 T时刻s处,数据的空间变化率为Δs(s),如式(3)所示。当数据变化趋势为增大时,Δs(s)>0,当数据减小时,Δs(s)<0。 Δs(s)=J(T,s)-J(T,s-1) (3) s与其左邻域s-1处的数据变化趋势一致,则s与其左邻域数据具有空间一致性。定义Cleft(s)为左邻域空间一致性,如式(4)所示。若Cleft(s)>0,s的左邻域满足空间一致性。 Cleft(s)=Δs(s-1)·Δs(s) (4) 与Cleft(s)同理,定义Cright(s),如式(5)所示,若Cright(s)>0,s的右邻域满足空间一致性。 Cright(s)=Δs(s+1)·Δs(s+2) (5) 根据空间一致性,可以排除异常的噪声点,当某个传感器失效或者出现较大噪声时,该传感器数据与左右两侧数据的变化趋势不同,不满足空间一致性要求。当Cleft(s)或Cright(s)为负数时,将数据点s删除,从而保证空间一致性。 1.1.3 时间一致性 t时刻s处数据的时间变化率为Δt(t,s),如式(6)所示: Δt(t,s)=J(t,s)-J(t,s-1) (6) T时刻的数据与前一段时间的变化趋势相同时,则数据具有时间一致性。定义Ctime(s)如式(7)所示。Ctime(s)>0,s处的数据满足时间一致性。 Ctimes(s)=Δs(T-1,s)·Δs(T,s) (7) 由于外部环境突变,可能导致传感器异常,例如电压电流变化、撞击等,通过Ctime(s)可以判断传感器当前时刻与历史时刻的数据变化情况是否一致,从而发现异常。 1.1.4 区域熵 N(s,R)表示一个位于s附近,半径为R的区域,覆盖数据矩阵JT×S从T-2R到T行,从s-R到s+R列的数据块。通过区域熵E(s)度量N(s)内的信息量。 E(s)表示为[10]: (8) (9) E(s)越大,表示N(s)中的信息越丰富,区域中的数据出现了显著的变化,是需要重点关注的特征区域。其中将E(s)最大的区域N(s)标注为特征区域regionF。 本文模型通过时空预处理保留同组传感器的数据特征,避免传统DS证据融合因个别数据异常,降低其可信度或剔除数据导致融合结果失去环境特征。本文时空预处理步骤如下所示。 步骤1:输入原始数据{J(t,s)|t=1~T,s=1~S}; 步骤2:根据式(2),计算空间均值; 步骤3:计算T时刻各位置数据与空间均值的差值,当某位置处的差值绝对值大于等于阈值σ时,标记为争议点数据si; 步骤4:根据式(3)~式(7),计算疑似争议点数据si的空间一致性及时间一致性,剔除异常数据; 步骤5:根据式(8)、式(9)计算区域熵获得特征区域regionF; 步骤6:输出时空预处理后数据{J(s)|s=1~S′}。 其中,σ为传感器数据与目标时序数据均值差额的阈值,本文主要研究综合管廊甲烷气体传感器的数据融合,取经验值为0.15。其次通过时空预处理,剔除了部分位置处的异常数据及噪声数据,因而S′≤S。对于空间一致性,因存在特殊情况如目标传感器为边缘传感器,故若仅满足左侧一致或右侧一致,则认为其满足空间一致性。 D-S证据理论由Dempster和Shafer提出[11]。在D-S证据理论中,辨识框架Θ表示有限个完备而互斥的元素{θ1,θ2,…,θn},2θ为辨识框架幂集,证据理论通过定义基本信任分配描述元素之间的差异性。任一关注命题都对应于识别框架Θ的一个子集。若式(10)成立,则称m∶2θ→[0,1]为Θ上的Mass函数。 (10) 式中m(A)为基元的基本信任分配函数(BPA)。 若m(A)>0,则称基元A为焦元。所有焦元并称为BPA的核。信任函数(Bel)和似真函数(Pl)分别定义为: (11) (12) 对于辨识框架Θ中的命题(或事件)A,可构成信度区间[Bel(A),Pl(A)],用于描述命题A发生可能性的取值范围。即证据理论是利用信度区间来描述命题的不确定性。证据理论中Mass函数的赋值m(Θ)∈[0,1]用于描述未知性。需要指出的是依据贝叶斯全概率理论,全集的总概率P(Θ)=1。 基于Dempster规则,可获取独立证据m1和m2的组合或融合结果,如式(13)所示: (13) 多个证据组合时,Dempster规则满足结合律和交换律,这有利于信息融合系统的分布式实现。 针对综合管廊同质传感器的数据融合,传统的数据融合方式存在许多不完善的地方,比如在某一时刻部分位置传感器数据明显高于其他传感器均值时,决策系统可能将其归列为错误数据并将其剔除,未参与最后的融合处理,这类融合数据方式易丢失监测环境中的特征信息,对融合后的数据应用(例如火灾预警等)造成不良影响。为了克服传统融合方式的缺陷,本文利用对各传感器间的数据一致性,以所有传感器作为支撑目标传感器的证据,通过这些证据计算目标传感器的可信度,最后根据可信度对所有目标传感器进行加权融合。 对于多个传感器,选取任意一个作为目标传感器,将所有传感器作为支撑目标的证据。设目标传感器为J(n),n=1~S′。对于每个目标传感器,向J(n)提供证据支撑的证据传感器为J(i),i=1~S′。J(i)对J(n)的支撑程度称为证据的基本信任分配mi(n)。根据所有证据获得目标的可信度m(n)。若某个传感器数据在数值大小及时空信息明显异于其他传感器,即说明其他传感器不支持该传感器数据,则该传感器可信度较低。相反的,若其他传感器各类信息充分支持目标传感器,则该传感器数据可信度较高。 2.2.1 证据划分及信任分配 根据证据与目标的相对位置关系及特征区域位置,定义证据的基本信任分配。根据证据传感器与目标传感器之间的距离,将证据划分为邻域证据集ΨN和一般证据集ΨM。另外,特征区域regionF内的传感器组成特征证据集ΨF。根据不同证据集的特性确定不同的信任分配。 (14) (15) 当J(i)靠近J(n),认为J(i)为邻域证据,所有邻域证据组成邻域证据集ΨN。反之,若J(i)距离J(n)较远,则J(i)为一般证据,所有一般证据组成一般证据集ΨM。 (16) 邻域证据靠近目标传感器,对目标的支撑度大,而一般证据对目标的支撑度较小,因此,需要为邻域证据和一般证据确定不同的信任分配。mi(n)为证据传感器i对目标传感器n的基本信任分配。KN、KM分别是ΨN、ΨM中元素的数量。 (17) 若证据J(i)位于特征区域regionF中,则J(i)∈ΨF。此时,取消原来的信任分配,重新定义mi(n),其中2R+1是特征区域regionF的宽度。 (18) 通过时空预处理中的空间位置和特征区域信息划分证据,有效改善了DS信任分配过程,有利于后续根据证据的信任分配计算目标可信度。 2.2.2 信任分配更新 (19) (20) 其次,对于ΨN、ΨM、ΨF等不同集合中的证据J(i),定义wi(n)满足一定约束。设为J(i1)为所有J(i)中的一个证据,J(i2)为所有J(i)中的另一个证据。J(i1)、J(i2)对应的组合权值分别为wi1(n)、wi2(n)。wi1(n)和wi2(n)满足以下约束,如式(21)所示,L为全体传感器覆盖的总长度,当相邻传感器距离为1时,L=S。 (21) 式(21)的物理意义为:(1)若J(i1)、J(i2)都属于邻域传感器,则证据与目标的距离越近,组合权重越大,权值与距离成反比。(2)通过时空预处理所得的特征区域产生的特征证据比邻域证据更重要,因此特征证据的权重理应大于邻域证据及一般证据。(3)邻域证据比一般证据更重要,故邻域证据权重理应更大。 另外,当两个证据均为一般证据或者特征证据时,组合权重相同。 (22) 由此,完成证据更新。 2.2.3 证据组合 将所有证据对目标的支撑程度mi(n)组合在一起,计算目标可信度m(n),如式(23)所示: (23) 以可信度m(n)作为J(n)的权重,多传感器加权融合结果为J0,J0表示为 (24) 为验证本文算法的实效性及优越性,文献[12-13]中使用模拟软件FLUENT对综合管廊一个防火分区中各位置甲烷传感器的数据模拟情况以及文献[14]对综合管廊通风情况的模拟,建立实验数据集共10组,其中1~7组设置为甲烷存在泄漏,8~10组设置为甲烷无泄漏,并在第10组加入异常值干扰。因篇幅限制,仅列出第1组实验数据,如表1所示,其中位置为传感器线性排列放置的位置,时刻为传感器收集数据的时序,6为最新时刻。实验PC处理器为Inter(R) Core(TM) i7-4710HQ CPU @2.50 GHz,内存8.00GB,在Matlab2016环境下进行实验。 表1 第1组甲烷传感器监测值 最新时刻数据图如图2所示,其中特征区域传感器为3、4、5。从传感器数据图可以看出,传感器4附近位置发生甲烷泄漏,故该时刻此防火分区最终融合值应在0.5左右才能够有效表现甲烷泄漏情况。 图2 最新时刻数据图 本文以第1组实验为例,分别以位置1、4处的作为目标传感器J(n=1)、J(n=4),给出各证据的信任分配计算步骤: 步骤2:根据式(16)~式(18)计算各证据的初始信任分配; 步骤3:根据归一化约束式(20),权重关系约束式(21),计算各证据的组合权重; {wi(n=4)|i=1~8}={0.196,0.188,0.153,0.136, 0.136,0.05,0.07,0.07} {wi(n=4)|i=1~8}={0.039,0.144,0.198,0.198, 0.198,0.144,0.039,0.039} 步骤4:根据式(22)更新证据信任分配; 0.167,0.167,0.006,0,0}, 0.244,0.107,0.018,0.018} 步骤5:根据式(23)获得目标可信度,由式(24)计算最终融合值,J0=0.405。由于本文方法最终融合值较接近0.5,故能够快速有效地表现该时刻防火分区发生的甲烷泄漏情况。 表2 算法生成的证据对比 此外,对实验集中的10组实验数据进行数据融合实验,对比算法包括文献[8]的算法和算术平均法。实验结果如图3所示。 图3 数据融合结果对比 从图3中可以看出:对于无甲烷泄漏的第8~9组实验数据,3种算法的融合值基本一致,即ST-DS保持了传统数据融合算法的良好融合能力。对于无甲烷泄漏但存在异常值的第10组实验数据,本文算法与文献[8]算法均具有排除异常值的能力,其中文献[8]依据方均欧式距离剔除异常值,而本文算法通过时空预处理,充分考虑异常位置的数据变化情况,判断异常值。第8~10组实验结果表明,本文算法保证了在无泄漏情况下的数据融合精度。对于存在甲烷泄漏的第1~7组实验数据,ST-DS的最终融合值明显高于文献[8]的算法和算术平均法,融合值越高越容易触发泄漏报警,同时更快的引起监测人员关注。因此,融合值越高算法性能越好。 这是由于ST能够监测甲烷的时空信息,通过时空预处理,能够最大程度保留泄漏点的环境特征,从而合理分配证据融合中各传感器的权值。文献[8]仅通过方均欧氏距离阈值差距大小判断异常值,导致最终融合值的可靠度不高。算术平均法对数据的敏感性较低且无法排除异常值,如对于第4~5组实验数据,在泄漏点浓度较小时,其融合值与本文算法融合值的差异较小;对于第6~7组实验数据,在泄漏点浓度较大时,其融合值与本文算法融合值的差异较大。综上所述,ST-DS不再以单一数据的数值差距作为融合依据,对综合管廊甲烷浓度感知更加敏感,最终的融合结果能够对当时管廊甲烷环境起到表征作用,提高了最终融合数据的实用性和有效性。 综合管廊中的监测数据具有种类多、总量大的特点。本文选用甲烷气体浓度的监测为研究对象,以D-S证据理论为研究基础,结合综合管廊中甲烷气体传感器的布置方案,通过进行时空预处理的方式,充分挖掘传感器监测数据特有的时空信息,提出一种基于ST-DS的数据融合算法。实验结果表明,与其他文献算法相比,本文算法通过进行时空预处理不仅能够保留原有数据内的特征信息,而且能够消除异常值,为后续的数据应用提高了实用性及有效性。1.1 时空预处理方法
1.2 时空预处理步骤
2 基于ST-DS的数据融合算法
2.1 D-S 证据理论
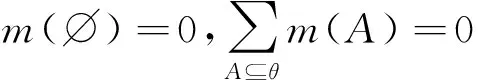
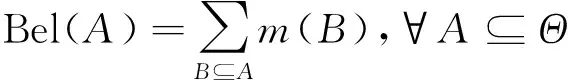
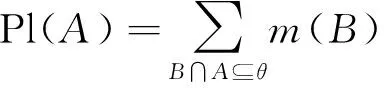
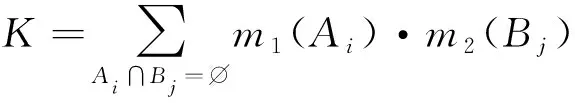
2.2 基于时空预处理的D-S融合方法
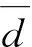
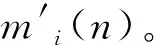

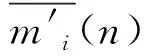
3 实验结果与分析

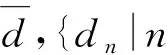
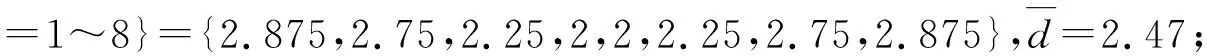

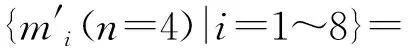


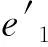
4 结论

