基于CQGA-LSSVM的桥式起重机主梁损伤识别

石瑞敏, 刘岩松, 马 旭, 臧春田

(1.中北大学机械工程学院， 太原 030051； 2.山西省起重机数字化设计工程技术研究中心， 太原 030051)

主梁是桥式起重机(简称“桥起”)中最主要的受力部件，在变载荷持续作业下部分焊接处可能会出现裂纹损伤，如若得不到及时处理，可能会发生损伤扩展，严重时更是会发生主梁断裂[1-4]。因此有必要定期对桥起主梁进行损伤识别与预测。

桥起主梁损伤实质是结构的损伤，对于结构损伤相关学者也进行了大量研究。安平和等[5]将曲率模态差变化率作为损伤评价特征，基于曲率模态通过量化突变，结合支持向量机实现了梁桥损伤的准确识别；石万[6]提出了一种基于经验模态分解和小波变换的损伤识别方法，并通过简支梁模型实验验证了所提方法的有效性；徐先峰等[7]在结构损伤模态频率的提取上将鲁棒性独立分析应用到钢结构框架比列模型中，大大提高了结构损伤特征提取准确率；为了改善桥起主梁损伤识别效果，徐红波[8]在原有识别技术上引入了改进粒子群算法，并通过修正的有限元技术模型进行验证，虽能准确判断结构实际状态，但在位置识别上还有待改进。

桥起主梁损伤的后果往往是主梁刚度减小，因此，现将常用于土木基建行业的刚度变化指标(stiffness variation index，SVI)引入到桥起主梁损伤评价中，结合云量子遗传算法(cloud quantum genetic algorithm，CQGA)优化后的最小二乘支持向量机(least squares support vector machines，LSSVM)实现桥起主梁结构的损伤识别，并完成相应的损伤程度计算，为其他结构损伤研究提供理论参考。

1 模型建立与处理

研究对象为山东某公司生产的QD型桥式起重机箱型主梁，其主梁截面简图如图1所示。主梁结构的基本参数如表1所示。

B为翼缘板宽度；H为腹板高；t1为上翼缘板厚度；t2为下翼缘板厚度；δ1为腹板厚度；b为主梁腹板间距图1 桥起主梁截面图Fig.1 Section of the main girder of bridge crane

表1 桥起主梁参数Table 1 The parameters of the main girder of bridge crane

在不影响分析与损伤识别的前提下，将主梁按单元长为500 mm进行等分，共45个单元，并进行等效刚度处理，得到的主梁力学模型如图2所示。

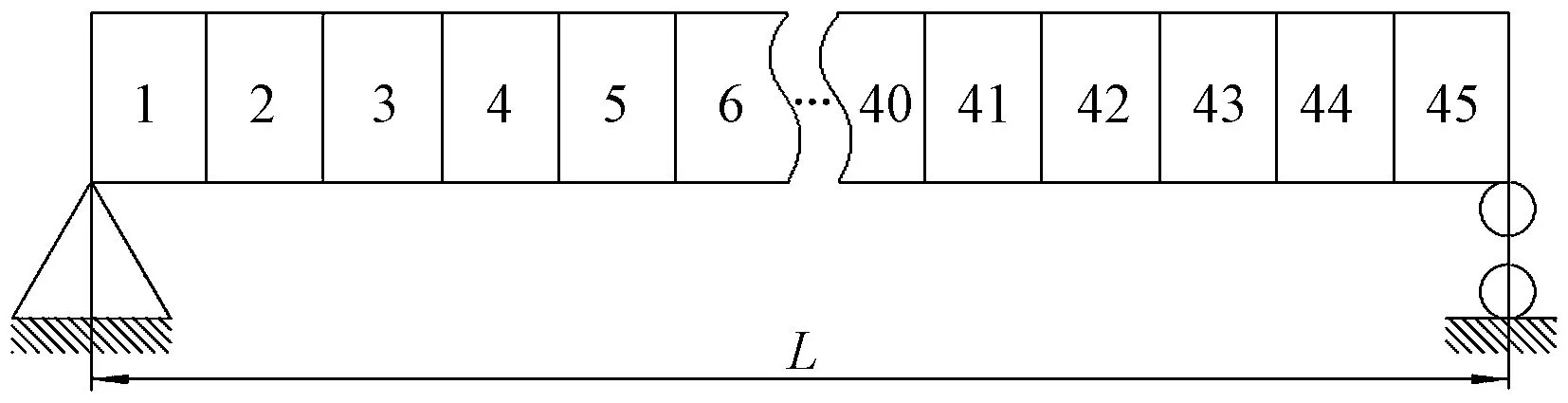
图2 桥起主梁力学模型Fig.2 Mechanical model of the main girder of bridge crane

2 评价指标

对主梁的损伤识别可转化刚度的计算。针对图2中的主梁力学模型，在模态小幅振动作用下，对于等分桥起主梁中的各个单元截面的抗弯刚度EI可表示为

(1)

式(1)中：EI为梁的抗弯刚度；M为截面的弯矩；φ为位移模态;ν为曲率模态。

若在主梁的第i个单元上强加第m阶模态的惯性力，可得第m阶模态单元的节点弯矩，即

(2)

式(2)中：ωm为m阶模态振动微量；ρ为密度；A为截面积；V为剪力。

初设目标函数为Q，为了减少计算误差，将曲率差值降低到最小，采用惩罚函数法进行计算，并通过调整参数α和β来实现曲率获取，Q表达式为

(3)

从式(3)中可知，在损伤位置及程度均不清楚的情况下，惩罚函数法中α和β不易选取，综合考虑采用中心差分法进行曲率模态获取，再依据式(1)完成刚度计算。通过对比计算损伤前后的刚度，即可得到用于评价结构损伤的刚度变化SVI，定义为

(4)

式(4)中：EId和EIu表示损伤前后的EI。

结构的损伤可改变结构的动力学特性和模态特性，因此若主梁出现局部损伤，则在该部位SVI值会发生显著改变。

3 LSSVM原理及优化

3.1 LSSVM原理

针对SVI该评价指标在迭代计算时过程复杂、拟合精度偏低等缺陷，同时为了避免二次规划等问题，引入LSSVM并将其应用于桥起主梁结构损伤识别。LSSVM用经验误差平方代替非负松弛因子，用等式约束代替了不等式约束[9]。LSSVM回归优化问题为

(5)

式(5)中：w为权向量；ε为误差变量；φ(xi)为非线性映射函数；b为偏差量；δ为误差惩罚因子。

采用拉格朗日法进行优化问题求解，即

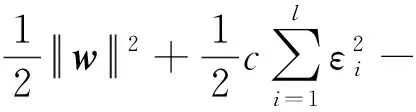
(6)

式(6)中：αi为拉格朗日乘子；c为正则化参数。

定义核函数K(xi,xj)为满足Mercer条件的对称函数，写作

(7)

式(7)中：xi为输入向量；xj为径向基函数的中心；σ2为径向基核函数。

根据Karush-Kuhn-Tucker优化条件，优化问题可转化为线性方程，即

(8)

求解上述方程可得相应的LSSVM最优线性回归函数，可得

(9)

3.2 LSSVM的优化

LSSVM模型的拟合精度与泛化能力通过参数c和σ2体现，因此最佳模型参数的选择对预测结果至关重要。为了让LSSVM能够得到良好的预测效果，需对LSSVM中模型参数进行优化调整。

云量子遗传算法(CQGA)作为一种结合了云理论和量子理论的新型遗传算法，不仅弥补了传统遗传算法搜索速度慢、早熟收敛等缺陷，在避免选择的压力的同时保证了种群多样性[10]。综合考虑选择使用CQGA对LSSVM中模型参数进行优化。

在种群的进化过程中，CQGA采用X条件云发生器对个体进行交叉、互换变异操作，在算子生产之后，对选取的优秀染色体进行重新编码构建，直至求出最优可行解。算子生成公式为

(10)

量子态的演化主要通过量子门的幺正变换来实现。为提高量子染色体叠加态的概率幅进化效率，选择通过量子旋转门来实现种群更新[11]。量子旋转门为

(11)

式(11)中：δθ=g(α,β)θ，g(α,β)为旋转方向，θ=D(αi,βi)Δθi，D(αi,βi)值可从旋转角度表中获取[12]。

量子门旋转角步长Δθi计算公式为

(12)

式(12)中：fB为最优适应度评价函数；Gmax为最大遗传代数。

在最优解求解时，最优适应度值g(X)min和平均适应度值g(X)avg关系为g(X)min≈g(X)avg，因此可将|g(X)min-g(X)avg|≤ε作为CQGA的收敛准则。CQGA优化LSSVM模型参数具体流程如图3所示。

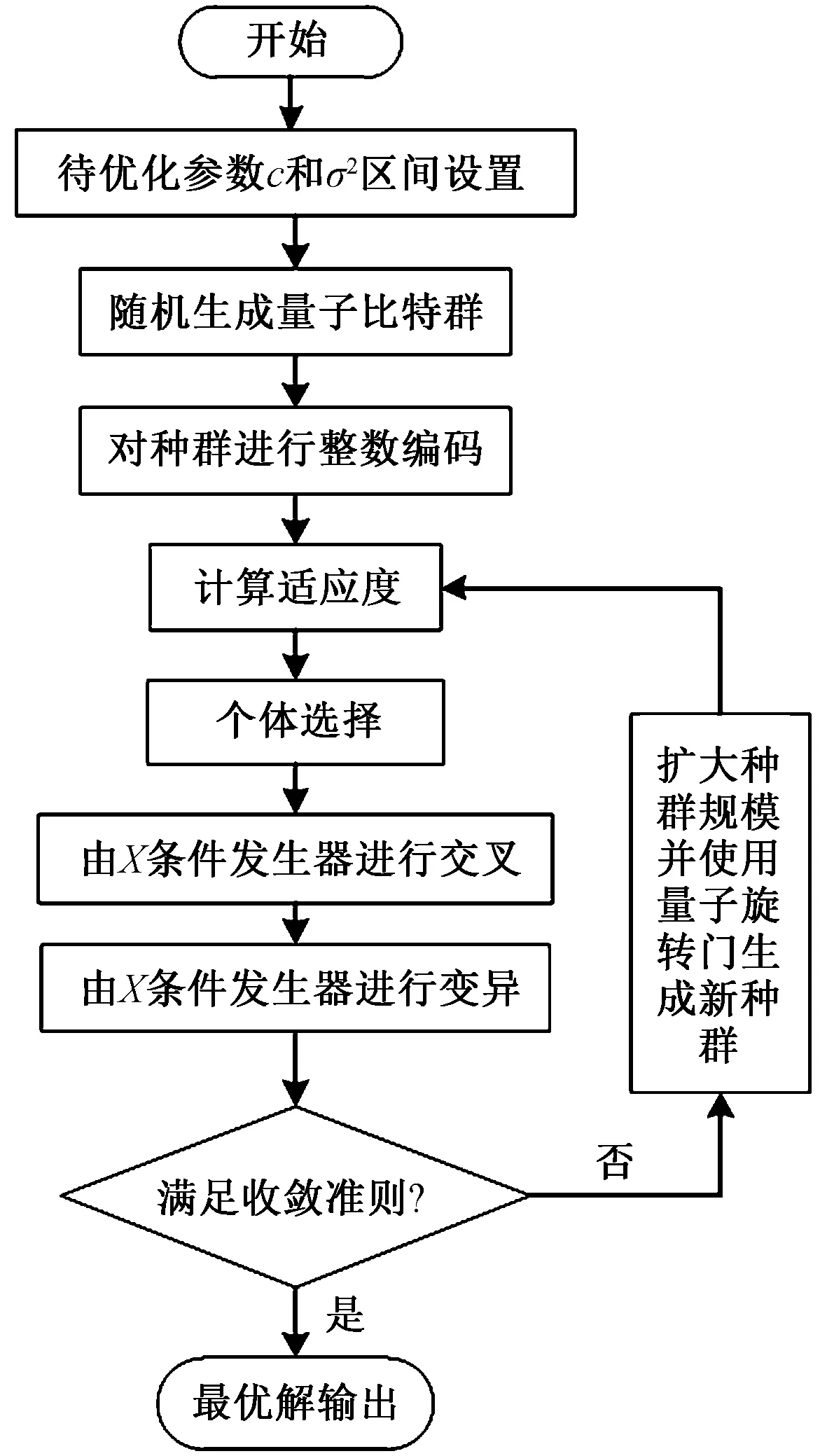
图3 LSSVM优化流程Fig.3 The optimized flow of LSSVM

4 实验分析

实验中选择桥起主梁的第一阶模态数据进行损伤识别及损伤程度预测。损伤单元选取及损伤因子设置如表2所示。

表2 损伤单元选取及损伤因子设置Table 2 Selection of damage units and setting of damage factors

为充分还原现场工况，提高仿真的真实性，在实验中对桥起主梁的模态参数加入高斯白噪声进行噪声模拟，噪声水平为5%。不同损伤类型下的SVI指标分析结果如图4～图6所示。

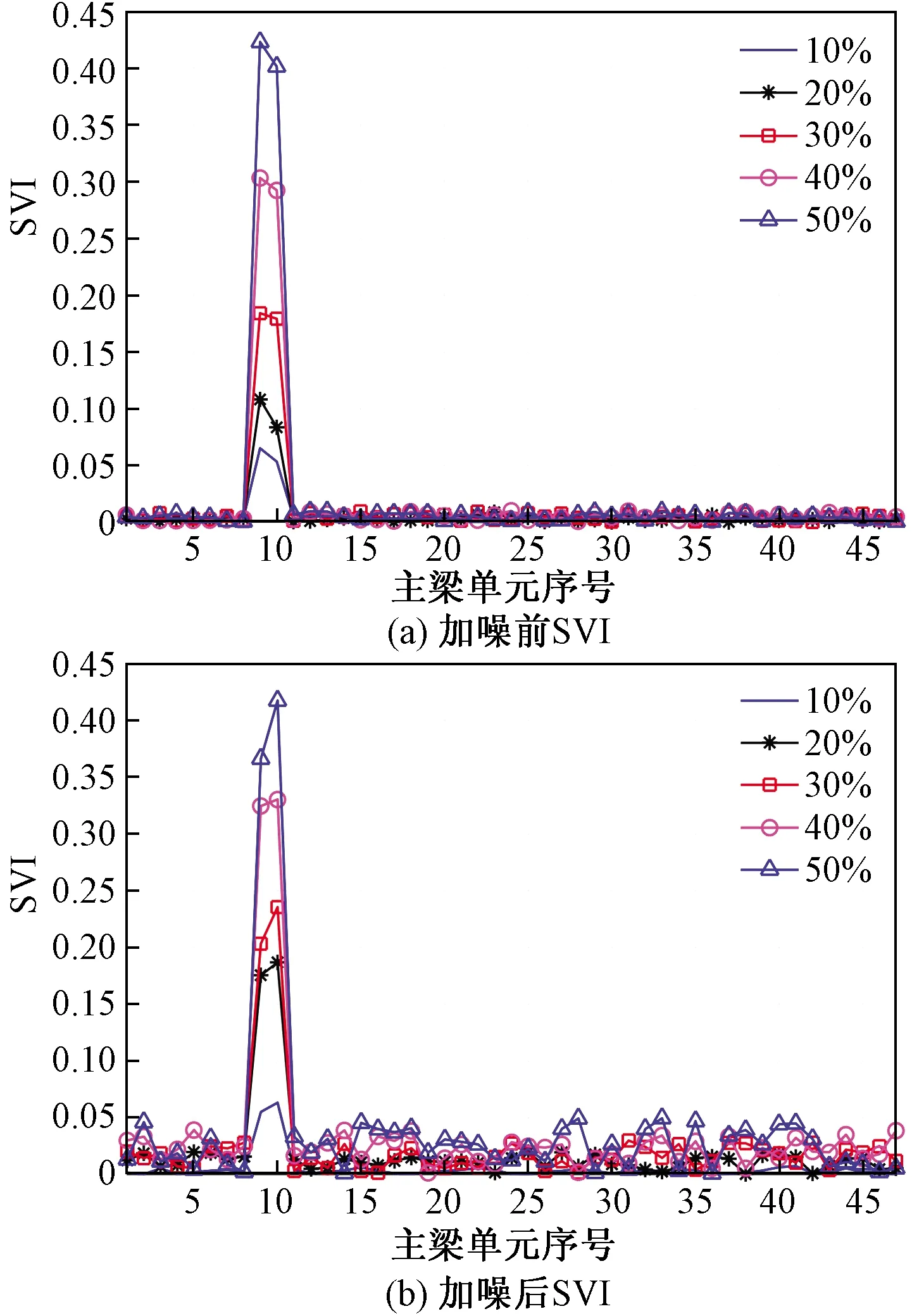
图4 主梁第9单元单损伤时各单元SVIFig.4 Each unit SVI of main girder when unit 9 is damaged

图5 主梁第39单元单损伤时各单元SVIFig.5 Each unit SVI of main girder when unit 39 is damaged

图6 主梁多损伤时各单元SVIFig.6 Each unit SVI of multiple damage of main girder

分析不同损伤类型下的各单元SVI结果可知：不论桥起主梁存在单损伤还是多损伤，均可根据SVI波动幅度完成损伤识别，进而确定损伤位置；在5%的高斯白噪声干扰下，SVI的抗噪能力良好，虽整体出现了小幅波动，但对损伤识别影响不大。

从损伤识别过程中可以看出，SVI会随着损伤因子增大而增大，损伤因子增大意味着损伤程度加深，而且在整体结构各单元SVI之间存在回归现象，因而在桥起主梁损伤定位完成后，有必要对损伤位置的损伤程度进行预测与评估。

为了验证 CQGA-LSSVM 性能，以第39单元损伤因子为25%、35%、45%和55%的损伤数据作为测试集，分别采用LSSVM和CQGA-LSSVM进行实验验证。

在CQGA-LSSVM实验中，选取主梁第39单元的 SVI 构成训练集，并按损伤因子的不同将损伤程度划分为5个等级，构造出桥起主梁的LSSVM 损伤预测网络。通过CQGA得出优化后LSSVM的最佳影响参数值：c=26.831，σ2=0.226，利用MATLAB训练得到LSSVM回归模型。39单元的损伤预测曲线及损伤预测的相对误差如图7和图8所示，分析结果如表3所示。

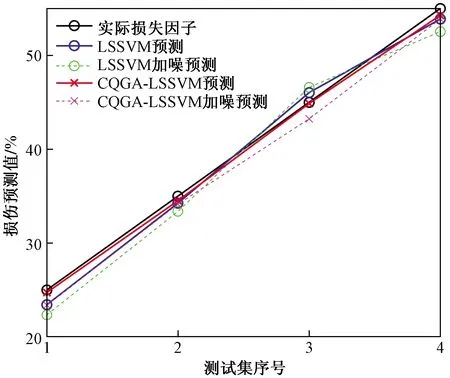
图7 主梁39单元损伤预测曲线Fig.7 Damage prediction curve of main girder unit 39

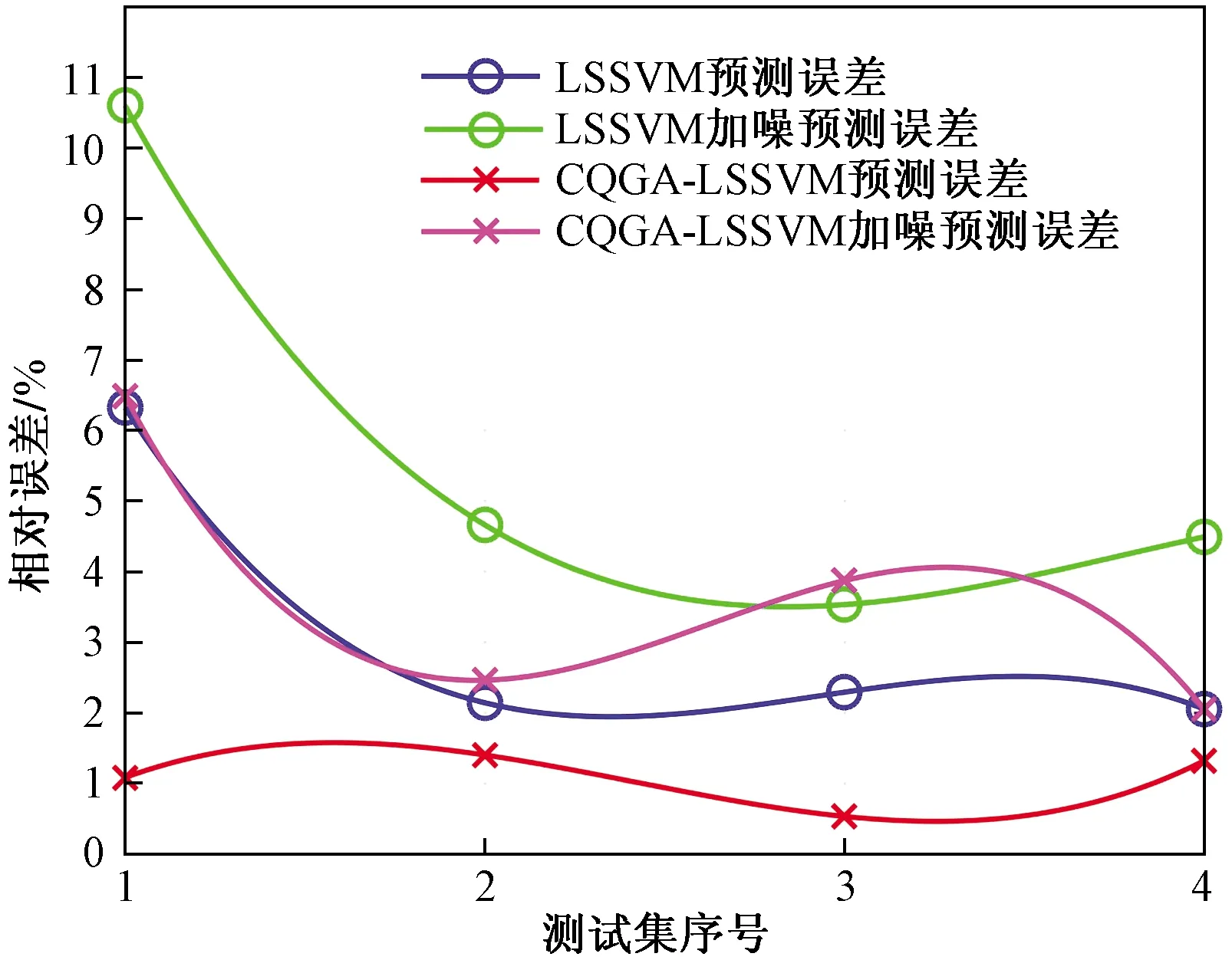
图8 主梁39单元损伤预测误差Fig.8 Error in damage prediction of main girder unit 39

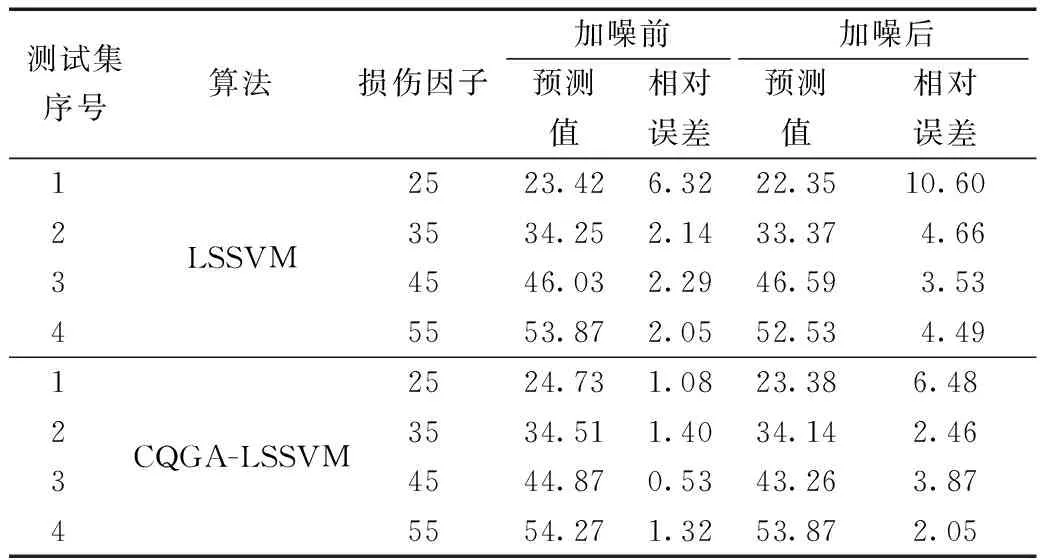
表3 损伤预测对比结果统计表Table 3 Statistical table of damage prediction comparison results

通过表3对比结果可以得出：CQGA-LSSVM较LSSVM的预测结果更接近于实际损伤因子，识别结果精度更高，具有更好的鲁棒性；在加入5%高斯白噪声后，其预测精度依然有明显的优越性。

5 结论

将SVI引入到桥起主梁损伤分析中，结合优化后的LSSVM，成功地实现了桥起主梁损伤定位及损伤程度预测。主要结论如下。

(1)创新性地将土木基建行业的SVI引入到桥起主梁结构损伤识别中，将主梁的损伤识别问题转化为桥起主梁局部刚度的计算，大大降低了损伤识别难度。

(2)采用CQGA对LSSVM的模型参数c和σ2进行优化，并采用 SVI 构成训练集对LSSVM进行训练，大大提高了LSSVM的拟合精度与泛化能力。实验结果表明：CQGA优化后 LSSVM的拟合精度与泛化能力增强，具有更好损伤识别能力及抗噪性。与传统LSSVM方法比较，更充分体现了CQGA-LSSVM方法的精确性与优越性。研究结论可为分析其他设备结构损伤奠定理论基础。