基于微分数学模型的数据挖掘方法

【摘 要】数据挖掘是处理大批量数据常用的手段，为了进一步掌握数据的发展规律，笔者基于微分数学模型开展了数据挖掘方法的设计，按照微分数学模型中的联合分布函数以及随机分布函数，构建数据的高纬度相空间，并以数学模型中微分数据的存储节点为特征获取依据，获取矢量数据集合的特征。为了减少数据拟合的工作量，在完成数据收集的基础上，进行空间维度的调整，将高纬度矩阵转变为低纬度矩阵。在数据收敛的作用下，通过对信息测度的调控，采用高斯核函数进行离散数据流挖掘，以此完成数据挖掘方法的设计。此外，提出仿真实验，建立实验仿真操作平台，使提出验证的方法更具备有效性，不仅对挖掘数据的命中率更高，还可适应不同环境下的数据挖掘方式，更具备实际应用价值。

【关键词】微积分;数据挖掘;数学模型

数据挖掘是指借助辅助性计算工具，在大批量的数据集合中，采用指定算法找出隐藏在数据集合中的某种规律性。随着当下社会生产的迅速发展，环境中数据监测量同步增大，可明显地发现传统数据挖掘方法在大批量数据处理及分析下的压力增大，虽然在指定时间内完成的数据挖掘量依旧较大，但数据的命中率较低，挖掘的数据层次较浅[1]。为了更好地解决这一问题，本文引入了微分数学模型。此模型是按照微分数学计算中的逻辑方法，利用数学语言构成的科学工程。目前数学模型已经是数学计算过程中不可缺少的计算工具[2]。本文基于微分数学模型的应用，设计数据挖掘方法，以期加大对数据集合的处理，提高处理数据集合的完整性与规范性。

1   数据挖掘方法

1.1  基于微分数学模型获取数据信息流的互信息特征

对于在不同渠道获取的数据集合，根据信息资源来源的不确定性，按照微分数学模型中的联合分布函数以及随机分布函数构建数据的高纬度相空间[3]。假设将点模型中分布的微分数据集合表示为 L={ l1，l2，l3，…，ln }，应控制模型中的微分数据与空间维度数据 N={1，2，3，…，x }集合具有一一对应的特点[4]。设定 T 为云环境下数据流的互信息特征表达方式，根据上述提出的对应特点，对 N 维度数据进行空间重构。重构的过程如下。

公式（2）中：F 表示在混合数据流环境下，与微分数学模型相匹配的有限矢量数据集合; f 表示集合中的子数据，E 表示模型中的微分动态化数据，s 表示数据在空间中的嵌入方式。根据上述计算公式，对获取的数据流集合进行样本压缩，以此获得聚合后数据信息流的互信息特征，以数学模型中微分数据的存储节点为特征获取依据，对上述计算的矢量数据集合进行特征提取。计算过程如下。

公式（3）中：表示数据信息流的互信息特征，p 表示数据分布存储阶段，q 表示数学模型中微分数据的存储节点，k 表示特征提取的云环境，i 表示获取行为的发生次数，f 表示数据的非线性时间排序。通过上述公式的计算，整合云数据的初始值，完成对数据信息流互信息特征的提取。

1.2  离散数据的拟合与挖掘

使用上述获取的数据信息流互信息特征，分析不同层面数据之间的关联性，并采集数据中最大指数的频谱特征集合。在此过程中，可使用 Lyapunove 算法建立高纬度数据矩阵，将完整型数据与离散型数据一并列入矩阵集合中。为了减少数据拟合的工作量，在完成收集数据的基础上，进行空间维度的调整，将高纬度矩阵转变为低纬度矩阵。此过程可用如下公式表示。

公式（4）中： k 表示数据频谱特征，c 表示数据流适度值，表示矩阵空间维度。在完成矩阵降维的同时，进行离散型数据的擬合，拟合过程如下。

公式（5）中：J 表示数据流拟合中心矢量，m 表示数据在拟合过程中的非线性扰动误差，O 表示拟合特征目标函数，W 表示数据拟合关联规则。在完成数据的拟合后，根据离散数据的表达方式，对其执行层次挖掘指令。在最小迭代次数和收敛的作用下，调控测度信息，采用高斯核函数进行离散数据流挖掘，核函数表达式如下。

公式（6）中：β 表示关联数据排列顺序，Q 表示数据挖掘最大调整量，S 表示数据子序列，R 表示数据逆变。根据计算公式，完成基于微分数学模型的数据挖掘方法设计。

2   仿真实验

2.1  实验准备

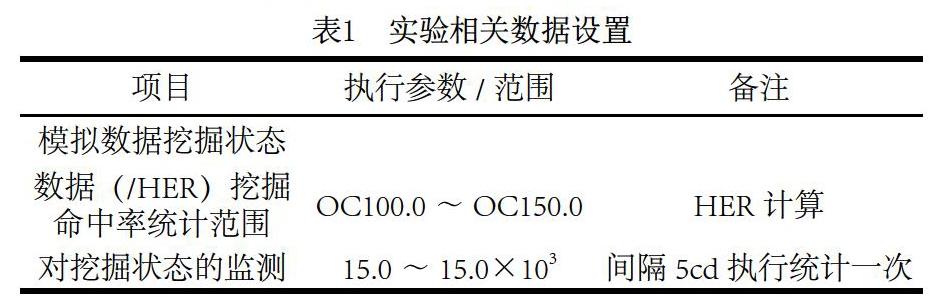
结合当下社会数据量的增长趋势，在此提出一个简单的仿真测试，检验本文提出数据挖掘方法的有效性。为了确保实验结果的准确性，采用搭建仿真实验操作台的方式，模拟此次实验的发生环境。使用4核8线程的计算机 CPU 作为实验的仿真平台，并将 Matlab7.0作为测试软件，数据挖掘的样本选择国家大型数据库开放性网络平台为本文实验提供的数据（MP IL 25.0中的数据集合）。本文实验选择数据库中的随机20组数据作为研究数据对象集合。要求这20组数据集合的规模从500.0Mbit 到 5000.0Mbit ，呈逐步上升趋势。实验过程中，为同组数据提供不同的挖掘环境，分别使用本文设计的基于微分数学模型的数据挖掘方法及传统数据挖掘方法，对选择的数据集合进行挖掘，以数据命中率为方法评估的指标，根据对挖掘环境的监测与分析，设计本次实验的相关指标参数，如表1所示。

根据表1的实验参数及实验环境，将本文数据挖掘方法定义为实验组，将传统数据挖掘方法定义为本次实验的对照组，分别使用两种挖掘方法进行不同环境下的数据挖掘工作，控制影响实验结果的相关变量，以此完成此次仿真实验的实验准备。

2.2  实验结果分析

根据上述的实验准备进行此次数据挖掘实验，记录实验过程数据，整理数据，并将其绘制成表2所示的实验结果。

根据上述表1中统计的数据可知，在不同的数据挖掘环境下，无论是传统方法或是本文设计的方法，均可执行对应的数据挖掘工作。但进一步分析表格中的数据发现，本文数据挖掘方法对于挖掘数据的命中值均在命中范围内，传统方法在环境1与环境3的实验中的数据命中值超出了实际范围，表明挖掘的数据结果不具备研究价值。因此根据上述实验结果得出此次实验的结论：相比传统的数据挖掘方法，本文提出的基于微分数学模型的数据挖掘方法更具备有效性，不仅挖掘数据的命中率更高，同时还可适应不同环境下的数据挖掘方式，更具备实际应用价值。

基于微分数学模型的应用，本文开展了数据挖掘方法的设计。采用设计对比实验的方式验证了提出的方法在不同状态下具备一定的可使用性。但由于本文进行的实验受到实验场地及实验设备的限制，实验的最终结果可能与实际结果存在一定偏差，为此在后期的研究中，可应用本文实验提出的环境，重构实验过程，完备实验中需要的设备，提高数据挖掘方法检验结果的真实性与准确性。

【参考文献】

[1]陈志雄.基于hadoop平台的分布式数据挖掘系统的设计探讨[J].数字技术与应用，2017（1）.

[2]梅毅，熊婷，罗少彬.复杂属性环境下NoSQL分布式大数据挖掘方法研究[J].科学技术与工程，2017（9）.

[3]熊亚军，孙兆彬，李梓铭，等.基于数据挖掘算法和数值模拟技术的大气污染减排效果评估[J].环境科学学报，2019（1）.

[4]李晓峰，李东.基于SOM聚类的多模态医学图像大数据挖掘算法[J].西安工程大学学报，2019（4）.

【作者简介】

常天兴（1982～），男，汉族，山西晋中人，硕士研究生，讲师。研究方向：基础数学。