小学数学活动经验积累的“三注重”

黄雪萍

摘 要：《数学课程标准》将“基本活动经验”从“知识范畴”中单列出来，把积累数学活动经验作为一项重要的教学目标，是新课程理念的重要标志。教师开展有效的数学活动，为学生提供“主动建构”的平台，通过“新知”与“旧知”、“操作”与“表达”、“体悟”与“统整”相结合，建立连接，关注过程，重在思考，引领学习者经历“数学化”过程，能帮助学生积累活动经验，将认知和实践内化为经验和智慧，进而促进数学素养的提升。

关键词：小学数学;数学活动;活动经验

一、注重新知与旧知相结合，激活经验

新课程强调教学应以学生的认知水平和已有的经验为基础。这就要求课堂教学要关注学生的认知背景，找准新旧知识的结合点，探明学生已有的数学活动经验，建立连接，帮助学生建构知识，迁移基本数学活动经验。

（一）创设生活情境，激活“生活经验”

数学活动经验的积累是一个不断发展、螺旋上升的过程。它总是在原有的数学活动经验的基础上开展的，因此教师需要扎根“生活”土壤，分析并唤醒学生已有的生活经验，找准新经验的生长点，设计符合学生认知水平的教学活动，将学习和生活对接，为新课的教学打下基础。

如在教学《反比例》一课时，有教师设置了一个生活情境——往一个茶杯里倒水，让学生观察思考：从这个生活现象中你能找到变化的量吗？两个变化的量有关联吗？由于“倒水”在生活中随处可见，学生纷纷发言，有的学生说：“杯子里的水不断增加，所以水的体积是一个变化的量;杯子上面的空余部分不断减少，所以空余部分的体积也是一个变化的量。”还有的学生说：“水的高度也是一个变化的量，因为倒水时水面不断上升，而且随着水面高度越高，水的体积越来越大，所以水的高度和水的体积这两个变化的量是有关联的。”在此基础上，教师用表格记录水的高度和水的体积变化当中的一些数据，问：“这两个变化的量之间有什么关系？将这种关系用图表示，图像是怎样的？”由于有了前面现实情境中的观察，很好地激活了学生已有的认知经验，点燃了学生亲身经历探索的热情和兴趣，生活经验成了对接新知识，積累、内化新经验的桥梁。

（二）基于原有认知，迁移“数学经验”

学生的数学基本活动经验是学生在数学学习过程中，原有知识、法则、联系与新的基本概念、原理、方法等教学内容相互作用而产生和发展的，因此在数学教学中，教师要找准新旧知识的联系，以学生的原有认知为起点，唤醒学生的已有经验，使其逐渐迁移到新知的学习中来。

如教学《小数乘整数》时，笔者考虑到学生前面学习“小数加减法”已具有“借‘钱说话，通过小数转化为整数计算，再用数形结合的方法验证”的意识和经验，教师让学生尝试计算，借“图”明理。又如教学“长方体的认识”一课时，笔者思考——如何让学生更快的接触长方体的本质特征？如何帮助学生为以后学习其他立体图形的特征积累活动经验？最后笔者确定教学中先唤醒学生研究平面图形的活动经验（从边、角、顶点去观察和研究）后，笔者大胆放手，让学生从“数量、形状以及面与面之间的关系”去研究，引导学生观察、操作、验证长方体面的特征，形成探索方法。学生自己发现、自己讲解、自主构建知识，为后面探索棱、顶点的特征积累活动经验。这样，教师以学生所学知识为媒介，帮助学生积累了迁移与转化的学习经验，丰富了学生的数学素养。

二、注重操作与表达相结合，生成经验

动手实践是数学学习的重要方式，是数学活动经验产生的起点。学生的经验从实践操作中获取，学生在动手操作的过程中能获取感官体验。在课堂教学过程中，教师要注重引导学生“操作”与“表达”紧密结合，促进学生外显操作、内在思维和有机语言的深入融合，使学生的经验不断趋向丰富和深刻。

如教学《圆柱的表面积》一课，为了深化学生的学习认知，笔者设计四个教学活动让学生探究。活动一：（出示一个圆柱体）做这个圆柱体纸盒，到底需要多少纸？说一说你是怎样想的？活动二：想一想，圆柱的侧面展开是一个怎样的图形？你能想办法证明吗？做好后把你的想法和同学说一说。活动三：圆柱的侧面展开图的长与宽与圆柱有什么关系？怎样求圆柱的侧面积？活动四：用卡纸制作一个底面半径为2厘米、高10厘米的圆柱，做好后小组内说说你是怎样想的。整节课教师主要采用了“动手操作——探究思考——语言表达”的教学方法，从而使学生明白了操作与表达是密不可分的，可以使学生所学知识及时得到内化，并使学生积累到操作与表达的学习经验。

三、注重体悟与统整相结合，提炼经验

数学活动的本质还在于数学思维活动。教师在教学实践过程中，通过有效的数学活动，让学生经历操作实践、观察想象、分析综合、抽象概括、归纳演绎、类比联想等数学活动过程，注重学习反思与总结，增强学生对数学活动过程与学习方式的体验，感悟活动过程中蕴含的数学思想和数学方法，促进学生逐步形成一定的数学思维模式和思维习惯，进而丰富数学素养。

（一）引导学生“悟”数学，积累归纳概括经验

在活动中，由“经历”上升到“经验”，非常重要的是需要学生思维和感情的参与。在这个探究学习的过程中，学生会经历猜想、验证、得出结论的过程，此时引导学生反思，有助于学生知识型经验的获得。

如教学“百分数解决问题”时，有教师设计三个层次的活动。首先，在已经知道两种促销方式（A商场：打五折，B商场：每满100元减50元）基础上提出问题：“买一条230元的裙子，选择哪一间商场更省钱？”并让学生凭直觉猜想、计算后思考：明明感觉是一样的，为什么算出的结果不一样呢？其次，出示三个问题（1. 什么情况下优惠程度是一样的？2. 什么情况下优惠程度接近？3. 什么情况下优惠程度相差较多？）让学生先思考再举例说明并想想生活中哪类商品的价格更常见。最后，出示一组分段数据（见表）让学生计算不同促销方式所需的钱，让学生观察归纳，从而得出结论：促销方式看似相同，实际不同;看似不同，也有相同;购物时要用心分析数据，做明智的消费者。

可以看出，通过“猜想—验证—推理—归纳”的方法，促进学生进行数学思考和数学交流，让学生经历抽象、归纳、概括、推理等思维活动过程，有助于学生形成从特例入手得到一般化数学结论的思维模式，获得归纳概括的经验。

（二）引导学生“比”数学，积累类比联想经验

在开展了实践活动后，学生积累了一定的活动经验，但这些经验往往是零散而混乱的，需要教师引导学生经历类比与联想的过程，帮助学生将这些散落的知识进行结构化、系统化处理，促进学生的认知经验由低层向高层迈进。

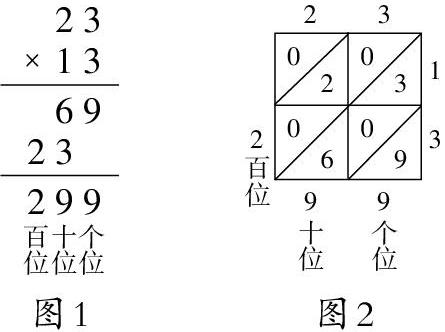
如教学“两位数乘两位数时”，教师通过探究例题“23×13”的三种计算方法，并对这三种方法进行对比，建立三种方法之间的联系，最终明确三种方法只是形式不同，但计算的道理本质上是一致的。

1.拆数口算：23×10=230;23×3=69;230+69=299;

2. 列竖式计算（图1）;

3. 运用画线的方法计算（图2）。

在“比”的活动中，学生建立和打通了以上三种方法的联系，深化了对于计算方法背后算理的理解，体验由此及彼、触类旁通的类比过程，更培养了学生把握事物之间的本质联系的能力。之后学生在计算“小数乘法”时，也能够立足于上述视角拓展思维。除此之外，学生还能够自主完成对活动经验的提炼和概括，可以将其拓展至“多边形面积公式的推导”“组合图形的面积计算”及除法性质、分数基本性质、比的基本性质的联系等知识的学习中。

参考文献

[1]中华人民共和国教育部.义务教育数学课程标准（2011年版）[M].北京：北京师范大学出版社，2012.

[2]郑少斌.积累数学基本活动经验的教学路径初探[J].小学数学教育，2019（01）.

[3]何亚玲.小学数学教学中学会积累基本活动经验的策略与方法分析[J].新教育时代（教师版），2018（21）.

（广东高州师范附属第一小学，高州525200）