论深度探究促规律理解

赵行娜

摘 要：学生在二年级已经学习了平均分，理解了除法的基本含义，“有余数的除法”是在此基础上学习除法后被除数有剩余的情况，理解“余数要比除数小”是这节课的教学难点，笔者在教学中让学生通过多维度的探究帮助学生真正理解“余数要比除数小”，设计对应练习，帮助学生内化规律。

关键词：小学数学;“有余数的除法”;规律理解

“有余数的除法”是人教版教材二年级下册第六单元的教学内容，这部分知识是表内除法知识后的延伸和扩展，也是今后继续学习除法的基础，具有承上启下的作用。笔者在教学中，将例1和例2作为一课时内容。在“余数要比除数小”规律的探索中，教材呈现了摆正方形的操作活动，帮助学生理解“余数要比除数小”的规律，通过这样单一的一次操作，学生只是记住这一规律，直接学习应用这一规律。这样得出规律，显然是不严谨的。

一、追根溯源

二年级学生的思维仍然具有直观性、具体性、形象性等特点，他们的假设、判断、理解等一系列思维过程都是在原有的知识经验基础之上进行的。而“余数要比除数小”的规律过于抽象，所以学生理解起来有一定的困难。那么在教学中应该让学生在具体情境中，通过丰富、有效的操作活动，使余数和除数两者之间的关系自然显现。

二、研究过程与内容

基于以上分析，笔者认为学生要真正理解“余数要比除数小”这个规律，必须要充分经历规律的抽象过程，建立充分的表象，才能使得规律自然显现。

（一）多维研究，促规律具体化

为了让规律抽象的过程更直观、更科学，学生探究的过程必须是多方位的。

1. 维度一：除数一定，被除数变化

问题呈现：通过分一分，知道了9支铅笔，每人分4支，可以分给2人，还剩余1支。如果铅笔的数量增加到10支、11支、12支……16支，还是每人分4支，分的结果会怎么样呢？算式又该怎么表示呢？

学生尝试在探究纸上分一分、算一算。完成后仔细观察分的结果和算式，说一说发现。在学生完成后，教师组织全班交流，介绍每次分的结果和算式。根据学生的回答，将结果展示在黑板上。

通过摆分一分的操作活动，引导学生根据自己平均分的结果列出算式后，再进行观察比较。在这次探究中，学生能够感悟到：在每人分4支的情况下，不管铅笔的数量变成多少，如果有剩余，最后的余数一定小于除数。这次探究是对“余数一定小于除数”这个规律的初步感知，培养学生勇于质疑的精神。

2. 维度二：被除数一定，除数变化

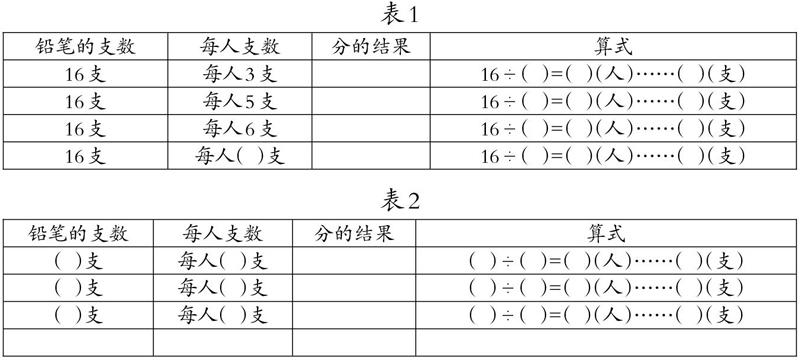
问题呈现：如果现在用这16支铅笔，每人分3支，结果怎么样？如果有剩余，可能会剩余几根？为什么？如果每人分5支呢？6支、7支呢？（见表1）

在这次探究中，学生能够感悟：同样都是16支铅笔，不管每人分几支，如果有剩余，最后的余数都小于除数。这次探究是对所感知的规律作进一步验证。

3. 维度三：被除数和除数都变化

提出疑问：通过刚才的探究，发现当除数不变，被除数变化的时候，如果有余数，余数小于除数;当被除数不变，除数变化的时候，如果有余数，余数也小于除数，这是为什么呢？

猜想：如果被除数和除数都变化了，结果会怎么样？

尝试探究：如表2所示。

本题没有给出铅笔的数量，每人的支数也没有确定，探究后组织学生讨论：仔细观察这些算式，你们又发现了什么？学生通过观察、比较，能够深切体会不管被除数和除数怎么变化，如果有剩余，余数始终小于除数。从一组到多组，从一维到多维，从感性到理性，就能形成系列较为充分的操作体验和直观感知，再通过分析和比较、抽象和概括，进而发现“余数小于除数”的规律，从而促进学生进一步理解余数、余数和除数的关系，理解有余数除法。

（二）适时追问，促规律抽象

为了提升学生的思考力，发展他们的思维，在学生探究后的讨论中，教师要适时追问，让学生可以进一步思考，提升思考层次，逐步达到抽象概括。比如在第一次探究后，教师提问：仔细观察这些算式，你们发现了什么？在学生关注到余数后，追问一：如果铅笔的数量继续增加，余数会是几？追问二：可能是4、5、6……吗？为什么？追问三：余数和谁有关系？是怎样的关系？为什么？在第二次探究后，教师提问：仔细观察这些算式，你们又发现了什么？追问一：如果每人分的铅笔数量继续增加，余数可能是几？追问二：为什么？通过多次追问，促使学生对有余数除法由感性认识上升到理性认识，进一步帮助学生加深对有余数除法的理解，感受数学知识间的相互联系。

（三）对应练习，促规律内化

学生三次探究之后发现了“余数小于除数”的规律之后，跟进相对应的巩固练习是必不可少的。以下“闯三关”的游戏模式，引导学生利用所学知识解决实际问题，进一步加深对规律的感悟，培养学生的应用意识。

第一关是利用“余数比除数小”的知识解决问题，通过独立思考、猜一猜、说一说、议一议等方式让学生明白：摆三角形时，剩余的小棒应少于3根，因为够3根小棒就能再摆一个三角形，摆正五边形依此类推。

第二关是3道选择题。从原先分铅笔、摆图形这些具体形象的事物中，抽象到算式的应用，每一道题都承载了不同的小目标。第一小题可以根据“余数小于除数”的规律直接判断。第二小题根据余数比除数小，可知余数可能是1，2，3，4，序号①出现了0，目的是明确余数最小是1，0即是没有余数，不需要写。第三小题是第一小题的逆向思维，帮助学生进一步理清余数和除数的关系。

第三关解决问题是借助“猫妈妈分小鱼”的情境，对规律的实际应用。图中每只小猫分得的小鱼条数与小猫只数同样多，说明除数和商是一样的，最后剩余7条，可见小猫至少8只，那么根据题意，可列式：8×8+7=71（条），也会出现□÷8=8（条）……7（条），渗透两者之间的联系。

多维度的探究、充分的直观操作，为表象思维和抽象思维提供了“脚手架”，学生充分经历探究规律的过程，适时的追问，帮助学生充分感知余数的含义，并逐步进行抽象，使得余数和除数的关系发现能够水到渠成，最后通过设计具有针对性、层次性和挑战性的练习，让学生更深入地感悟“余数比除数小”这一规律。

三、成果与分析

笔者在磨课过程中对探究过程进行这样的调整后，COP团队对这节课进行了数据采集和分析，我们发现：

1. 探究的深度。问题的类型中，更多的是推理性问题和创造性问题，在探究的深度和课堂生成的高度中，我们所关注的思维深度、对话深度、问题类型都接近，甚至高于全国常模数据，体现了探究过程中，学生能够跟着探究的推进做进一步思考和发现。

2. 學生的参与度。在S-T曲线图中，可以发现学生的行为要高于教师行为，说明探究过程中，学生能够积极参与探究、思考与表达，而不是为了完成教学内容，教师代替讲。在练习过程中，学生能够灵活应用规律，清楚表达，尤其能够感受学生的对规律的理解和思维的提升，大大提高作业的正确率。

参考文献

[1]张春洁.“有余数的除法的认识”教学设计与说明[J].小学数学教育，2020（Z2）.

[2]黄红军.善用对比，促进内化——人教版教材二年级下册“有余数除法”教学设计化[J].小学教学参考，2019（02）.

（浙江省宁波市奉化龙津实验学校，宁波315000）