哈特曼法焦度测量模型的误差分析及修正

杨金龙，贾宏志，金 涛，项华中，张大伟，庄松林

哈特曼法焦度测量模型的误差分析及修正

杨金龙，贾宏志，金 涛*，项华中，张大伟，庄松林

上海理工大学光电信息与计算机工程学院，上海 200093

为了减少屈光度测量误差，提高精度。本文针对哈特曼法焦度测量建立了较详细的误差模型，着重分析了光源的色散误差、入射光与透镜未垂直、光电探测器中心定位不准、透镜倾斜、光源光线主轴与透镜主轴未重合所引起的屈光度测量误差。结果表明，得出由于光电探测器上中心提取的不准确，会对最终的结果产生较大的误差。并由此提出了双重双线性插值结合拟合法来求取中心的方法，并证明了其有效性和准确性。

哈特曼光阑；焦度测量；误差模型；图像处理；中心定位

1 引 言

焦度计[1-3](屈光度计)是用于测量眼镜和接触镜片的顶焦度及棱镜度，以及确定镜片的光学中心、轴位等光学参数的仪器。其中，自动对焦式焦度计因其高分辨率、智能化的特点在实际生产生活中被广泛应用。自动对焦式焦度计的发展经过了三个不同阶段，前两代的自动对焦式焦度计使用线性传感器的单点检测原理，由于光路不密封、容易受干扰、依赖机械开关等导致测量存在误差，而最新的第三代的焦度计主要采用哈特曼光阑测量法，平行光通过镜片和哈特曼光阑板在光电传感器上所成图像与未经过镜片形成的光斑图像在位置上有相对应的变化，再根据光斑位置距离的变化计算出镜片顶焦度的光学参数。该方法不仅能有效地减少人为误差，而且能准确地测量镜片的光学参数，这是目前为止测量镜片光学参数的最简便实用的方法。近年来，镜片的研究领域主要集中在渐进多焦点镜片、自由曲面镜片、非球面镜片[4-6]，其镜片屈光度的测量本质上还是采用哈特曼法焦度测量，目前已有对前两代的焦度计误差分析模型[7-8]。但对于哈特曼法焦度测量方法并没有一套完整的误差模型。因此，本文对哈特曼测量法进行相对完善的误差模型分析，有利于之后焦度计测量的误差修正；而且通过分析误差模型，得出光电传感器上中心的定位不准确会产生较大的误差，提出了一种采用双重双线性插值法结合拟合法求取中心的方式，并证明其有效性和准确性。

2 哈特曼法焦度测量原理

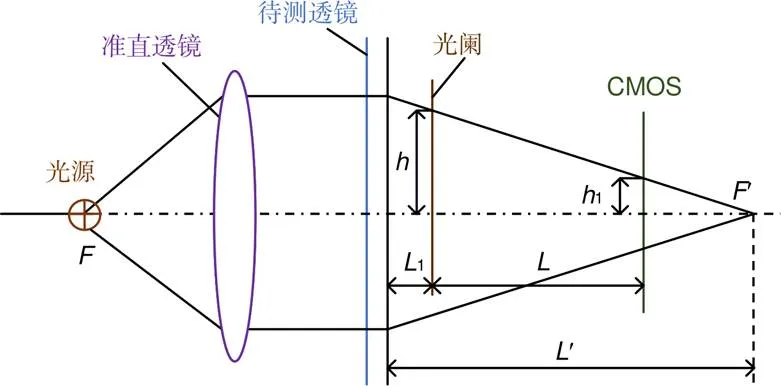
哈特曼法焦度测量法主要由光源、准直透镜、哈特曼光阑、光电传感器(CMOS)等部分组成。图1为哈特曼法焦度测量结构[9]示意图，光源发出的光经过准直透镜后形成平行光，平行光通过待测镜片后的出射光线穿过具有通光孔的光阑，成像在光电图像传感器上。当光路中没有被测镜片时，平行光通过光阑上的某一个通光孔后投影在光电传感器上，表示光电传感器上两投影光斑中心之间的距离，1表示放置待测镜片后在传感器上两个光斑中心的距离。因此，计算落在图像传感器上光斑中心的位置变化量，就可以得到镜片的屈光度。

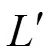
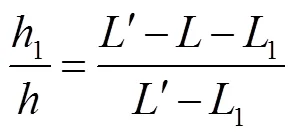
由式(1)可得镜片的焦距¢：

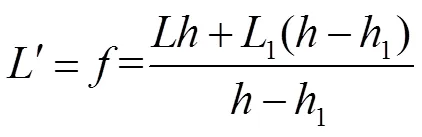
设、1、、1单位均为毫米，则屈光度¢(单位为m-1，通常用D表示)的公式：

式中：1可由光电探测器光斑中心坐标(x，y)得出，因此自动焦度计可通过测量得到的(x，y)计算待测眼镜片的屈光度。

由于式(3)是基于理想的同轴光学系统推导出来的，而实际的屈光度测量时，由于光源的色散误差、入射光与透镜未垂直、光电探测器中心定位不精确、透镜倾斜、光源光线主轴与透镜主轴未重合等原因都会引起屈光度测量误差。因此，下文针对这几种情况进行相应的误差模型分析。

2.1 光源的色散引起的误差

由于不同波长的光经过镜片后的速度不同导致出射方向的偏向角的不同，因此在光电探测器上的会产生不同的像点，常用阿贝数(d)来衡量镜片材料的色散能力，d表达式为

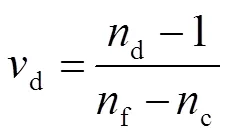
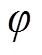
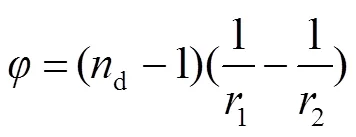
其中：1、2分别为前后表面的曲率半径，由于光的色散引起的顶焦度改变量为

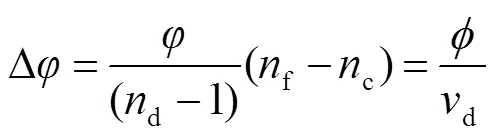
由式(6)可知，由于色散引起的顶焦度变化与阿贝数成反比，阿贝数值越大引起的顶焦度误差越小。由于人眼对黄绿光最为敏感，将波长为555 nm的视见函数称作人眼的最佳视觉函数。国际标准ISO 7944-1988规定了焦度计的测量标准波长为546.07 nm，在使用绿色光源[10](波长为543 nm)时，绿光无修正测试最大绝对偏差为1.5%，最小绝对偏差为-0.18%，均在5%以内。因此，即使没有阿贝数修正，也可以尽可能地减少色散引起的透镜屈光度测量误差，既减少了算法的复杂度，也不影响测量结果的准确性。

2.2 光阑与透镜之间的距离忽略不计引起的误差

图1中1表示待测透镜与光阑之间的距离，而待测透镜与光阑的实际位置关系如图2所示。

每个镜片的曲率半径不同导致1的不同。实验室所用的待测镜片正透镜直径是65 mm，负透镜直径是72 mm(镜片的中心厚度约等于0)，图2中相关参数的关系为

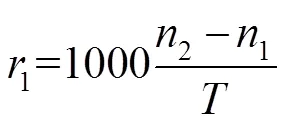
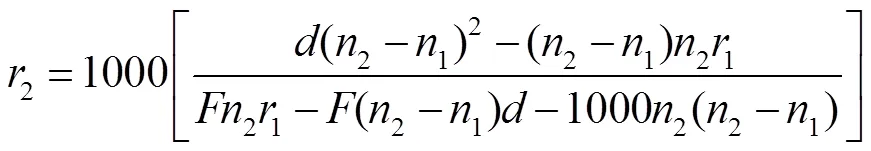
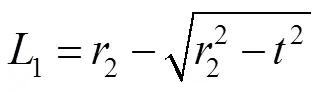
其中：1代表空气折射率，2代表透镜折射率，光阑的半径为，透镜的前表面弯度为。

得到-25D至+25D镜片对应的1在0.01 mm~0.15 mm变化，若1值忽略不计，则屈光度计算式变为

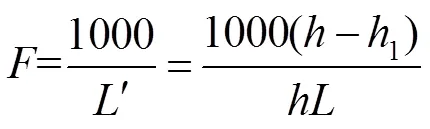
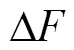
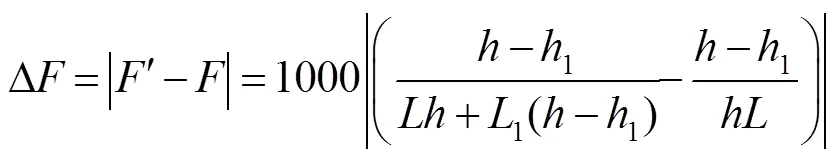
分别以+5D、+10D、+15D、+25D(本文屈光度误差取绝对值，所以负透镜同理)的透镜为例，让1从0.01 mm到0.15 mm变化，则屈光度误差曲线如图3所示。

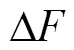
2.3 透镜倾斜所引起的误差

由于人为的失误或者透镜未固定好也会导致透镜倾斜所产生的误差，此时的屈光度测量模型如图4。

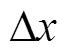
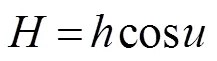
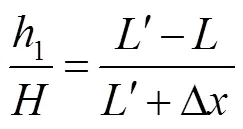
由式(12)~式(14)可得：

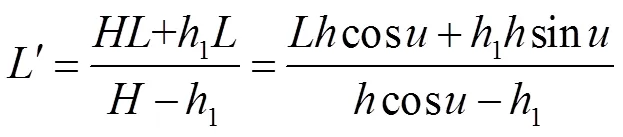
由于透镜倾斜，设它实际的焦距为，为

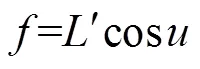
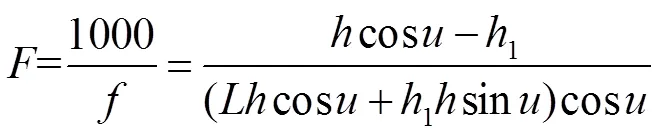
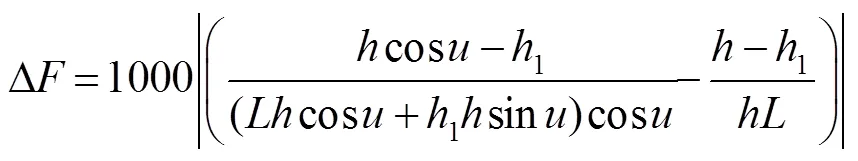
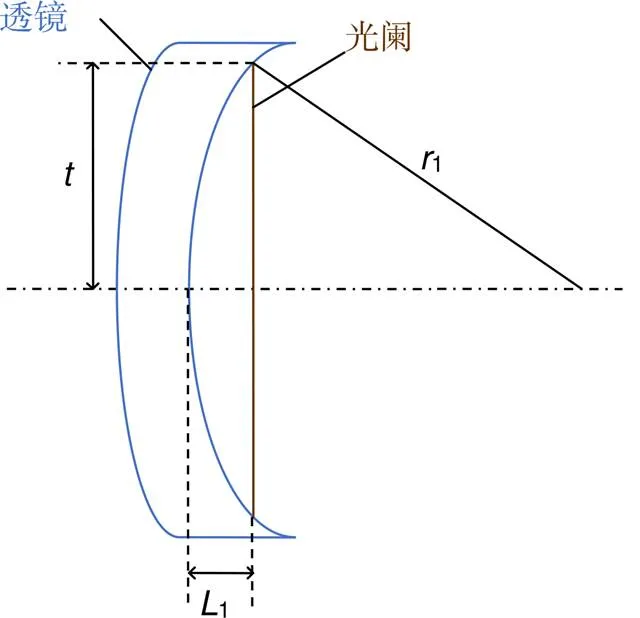
图2 透镜与光阑的实际位置关系图

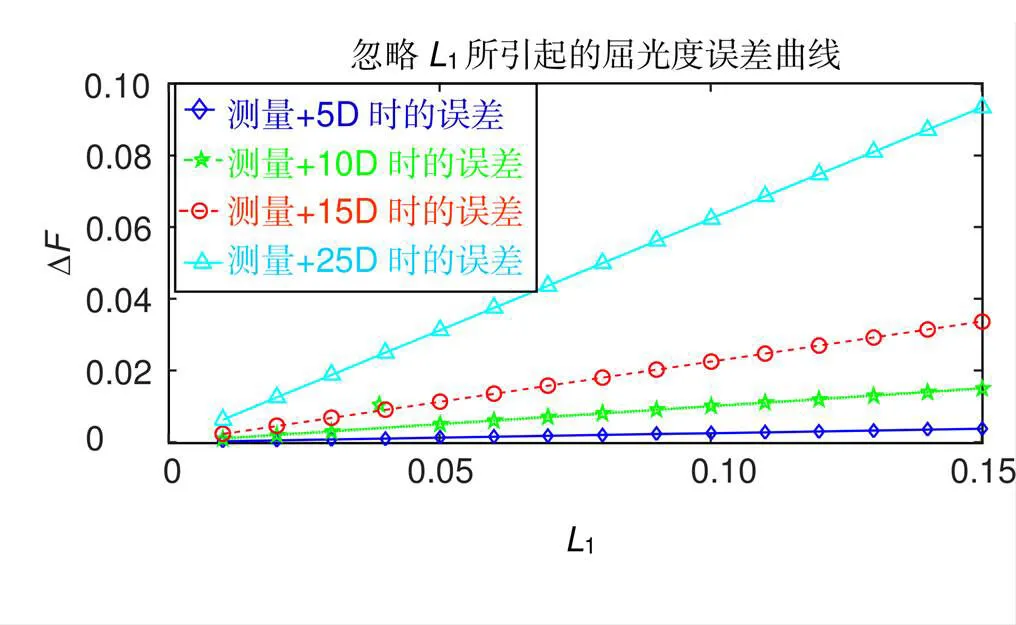
图3 L1所引起的屈光度误差曲线

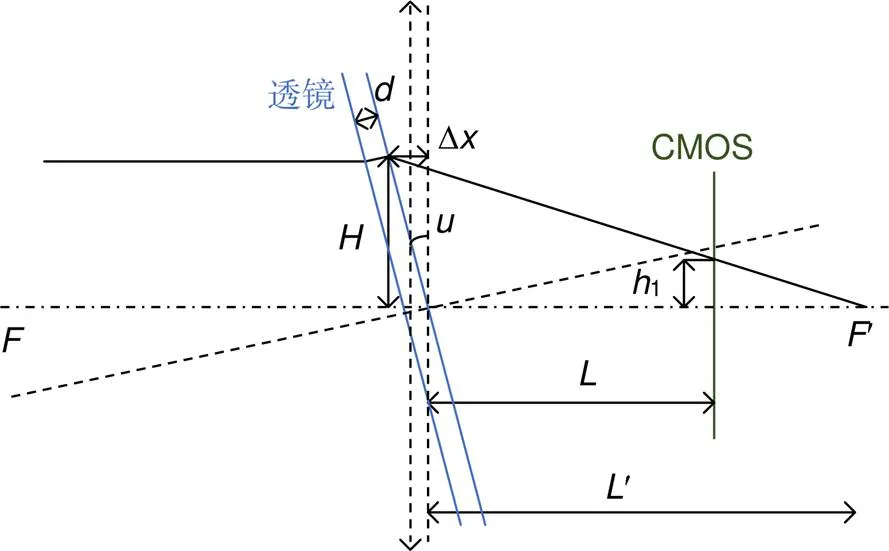
图4 透镜倾斜的测量模型

假设透镜的偏转角度从0°至5°变化，则由于透镜角度偏转导致的误差曲线如图5所示。

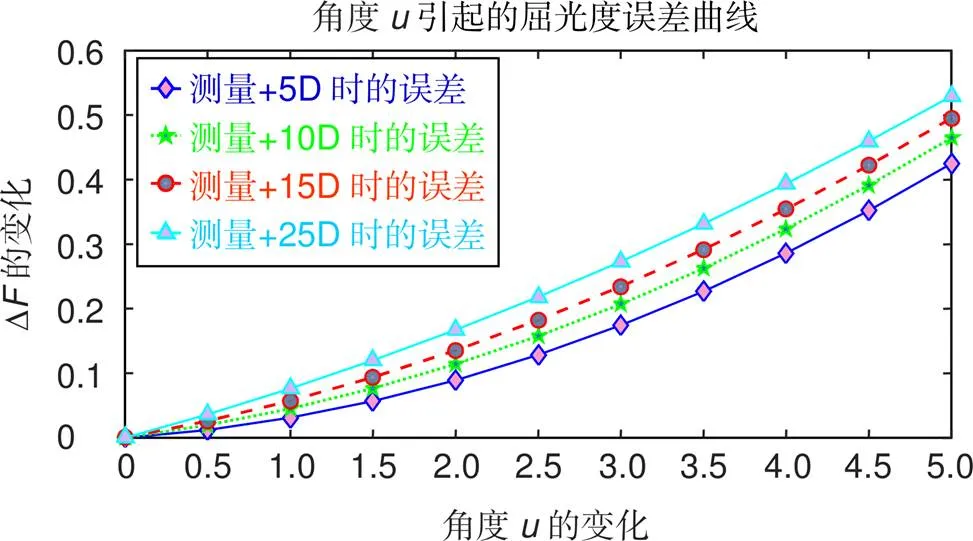
图5 透镜角度偏转导致的屈光度误差变化

由图5可知，透镜的倾斜角度对于大的屈光度镜片的测量误差会偏大，且呈现指数型的增长。当倾角为5°时，测量+25D屈光度时误差达到0.5293D，对最终的屈光度测量结果产生较大的误差，已经超出了国家规定的±0.25D的范围，因此在实验中务必保持透镜与入射的平行光相互垂直，否则会造成测量结果的不准确性。实验中待测透镜由弹性的伸缩杆所固定，根据伸缩杆的长度变化可以算出透镜的偏转角度，代入式(18)中，求出误差后可修正屈光度。

2.4 光源的光轴与透镜的几何中心轴未重合而导致的误差

由于光源的光轴与透镜的几何中心轴未重合会导致误差。设光源从轴外点斜射入透镜，此时的屈光度测量模型如图6所示。

图6中A到主轴的距离为2，¢到主轴的距离为¢2，由=¢/=¢/，得¢2=-2¢/1，光线的入射角的角度为，光点与透镜物方主平面的距离为-1，光线入射高度为，出射光线与主轴交点至光电探测器的水平距离为2，光电探测器与透镜像方主平面的距离为，出射光线在光电探测器上的投射高度为1，出射光线与主轴的交点与透镜像方主平面的距离为¢。由图6参数之间的关系可得：

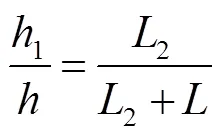
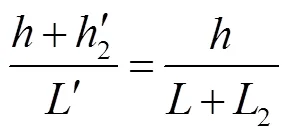
由式(19)、式(20)计算得出¢为

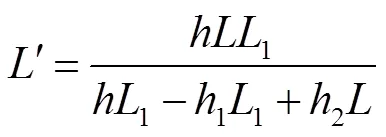
由高斯公式得：

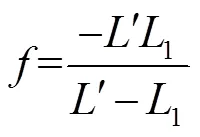
所以透镜的焦距为

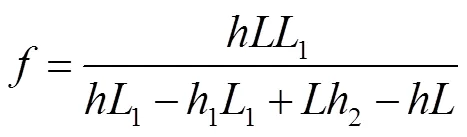
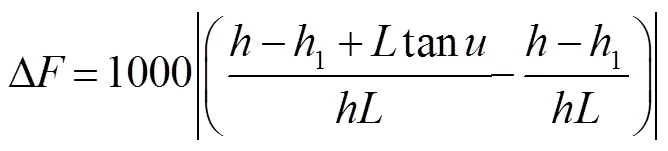
假定2为定值1 mm，角度从0°至1°变化，误差曲线如图7所示。

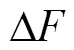
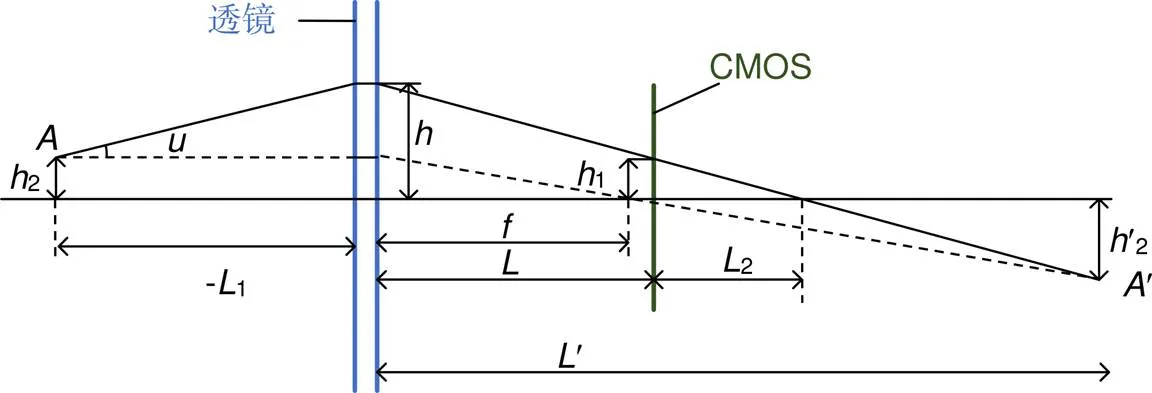
图6 主轴外光点射入透镜模型

2.5 光电探测器图像光斑中心定位不准确引起的误差

用表示光电探测器上两光斑中心之间的距离，当光电探测器上由于光斑中心定位不准确产生误差时，式(11)可算出屈光度误差：

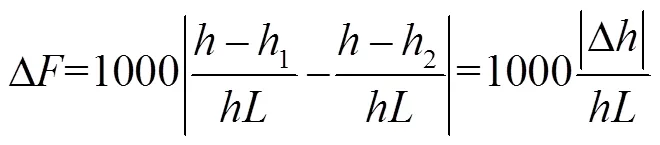
其中：1表示测量的距离，2表示实际的距离，(x，y)表示光斑中心的位置坐标，1、2的计算公式：

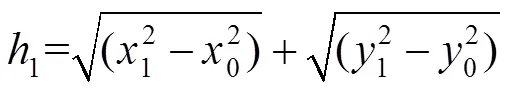
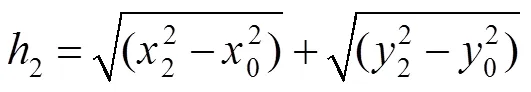
实验室所用的光电探测器中1像素点对应的尺寸为3.5 μm，由于光电探测器光斑中心之间的测量距离不准确所产生的屈光度误差曲线如图8所示。

由式(25)可知，像素差造成的屈光度误差与所测量的镜片的屈光度并无关系，图8显示了在1~10个像素点变化所产生的误差，待测镜片的屈光度误差与光斑中心的距离差成线性关系，且在10个像素的误差内，屈光度最大误差达到0.26D。因此，如果光斑中心的定位不准会产生较大的误差，并有可能直接造成测量结果的不准确。而光斑定位的误差主要分为系统误差和随机误差，系统误差主要由成像器件的非线性、像素尺寸的非均匀性构成。随机误差主要由于噪声，光电探测器[11-12]成像的分辨率的局限性导致的。而下文提出了双重双线性插值法结合拟合法来减小随机误差从而提高中心定位的精度，因此可降低屈光度测量的随机误差。

3 双重双线性插值法结合拟合法求取中心的方法

3.1 算法的整体框图

为了保证该方法的可靠性、准确性，需要建立一个标准的模型用来对比实验结果，本文采用如下方式：首先建立一个二元的高斯函数，得到一个三维的高斯曲面且此曲面的中心坐标为(x，y)，将函数值离散化得到对应灰度值的矩阵，将此矩阵看做一个理想的高斯光斑所对应的矩阵，再用圆拟合法得到中心坐标，最后采用本文所述方法计算灰度矩阵的中心，经过对比，判断该方法的有效性。整体流程如图9所示。

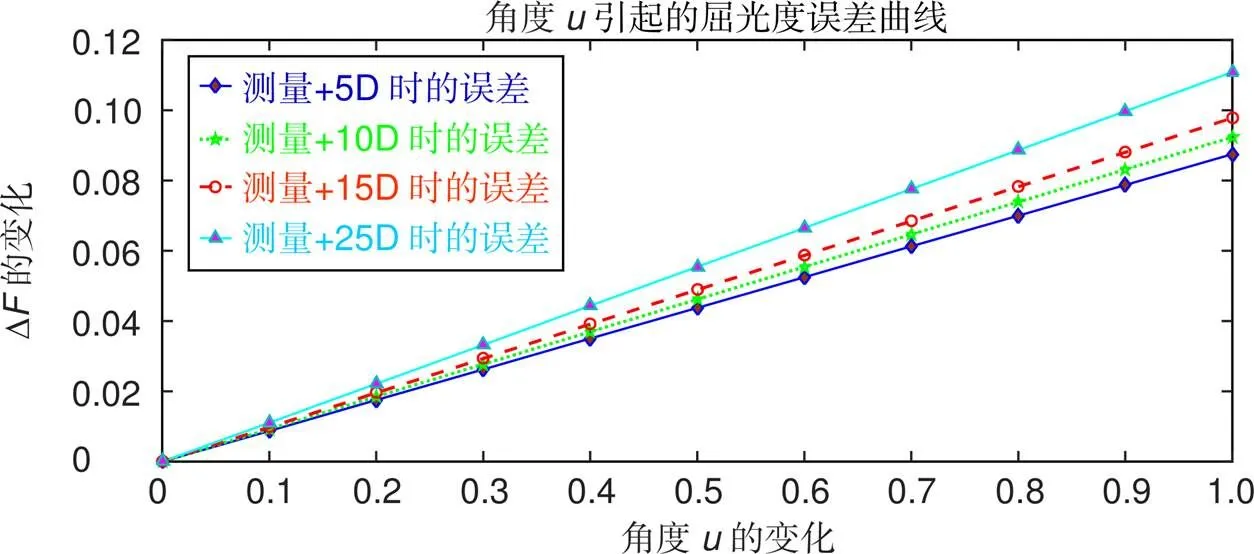
图7 光轴与透镜主轴的偏转角度导致的误差变化曲线

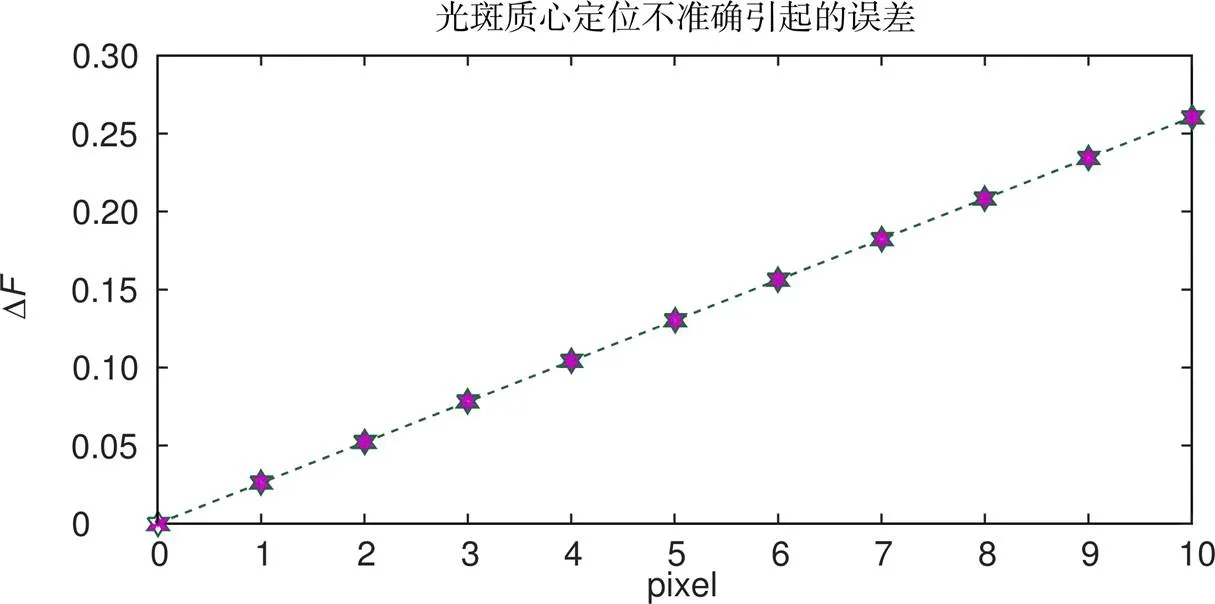
图8 像素差导致的屈光度误差变化曲线

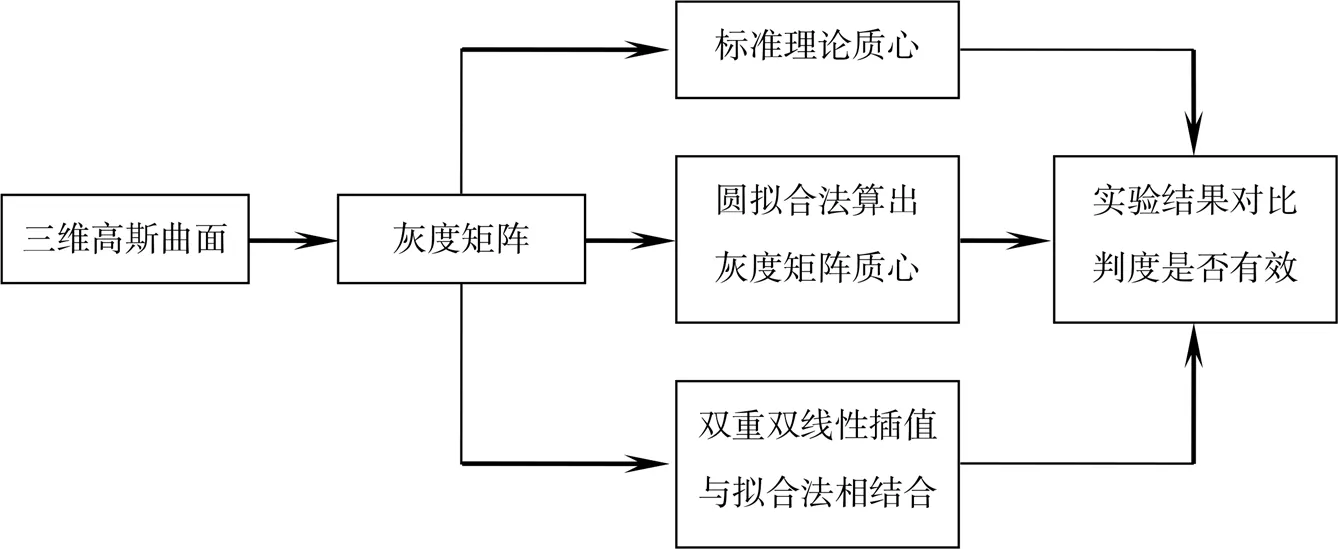
图9 算法的流程框图

3.2 详细的算法步骤

首先，建立二元高斯函数，如式(28)所示：

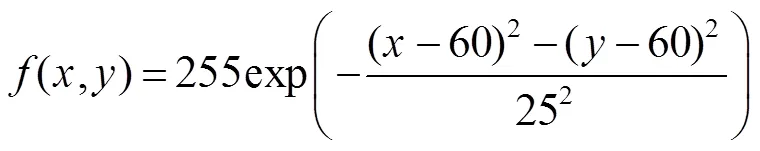
the用Matlab将此函数绘制成三维高斯曲面，将、两个自变量离散化取整得到一个120´120的矩阵，将矩阵的函数值离散化并且转化为unit8数据类型，得到相应的灰度矩阵，灰度矩阵所对应的高斯光斑如图10所示。

图10 高斯光斑所对应的灰度图像

图11 高斯光斑所对应的二值化图像

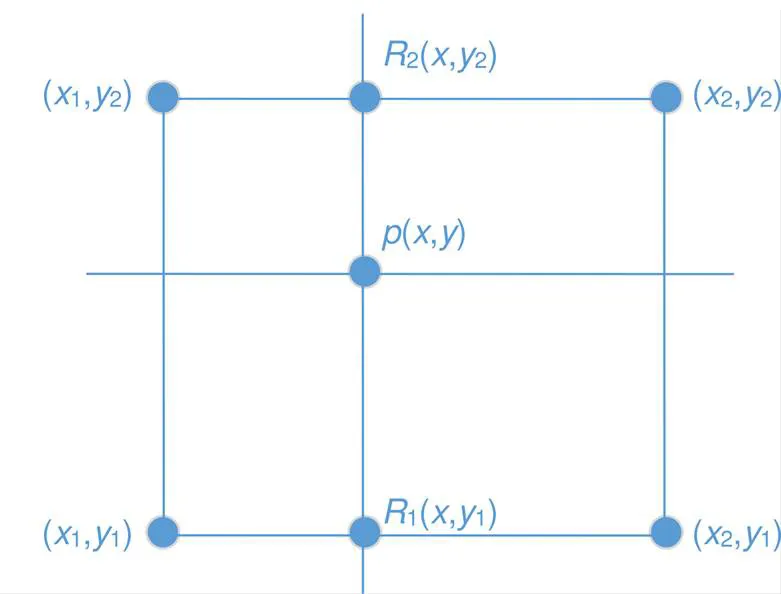
图12 双线性插值算法示意图

得到图像的灰度矩阵后首先进行图像[13-15]的二值化，本文采用直方图法来进行二值化处理，主要是通过统计像素值来寻找图像的两个高峰值，然后将阈值设为两个峰值之间的最小灰度值，得到的二值化图像如图11所示。

得到二值化图像后，采用Canny边缘检测法来采集图像的边缘信息。Canny算法能够有效地检查弱边缘，对噪声信号抑制作用较强，对边缘信息保留的细节多，然后使用圆拟合法对边缘信息进行处理，得到中心坐标1(59.4809，59.5895)。

由误差计算公式，如式(29)所示：

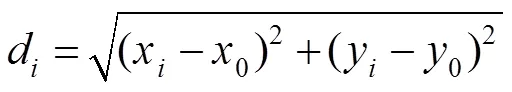
可以计算得到的中心坐标与理论坐标的误差1=0.438。

然后用二维双线性插值对理想光斑进行均匀细化处理，双线性插值本质上是对两个方向分别进行一次线性插值，如图12所示。首先在要插入点的(，)选取邻近4个点，根据(1，1)与(2，1)对1点的值进行线性插值，然后根据(1，2)与(2，2)对2点进行线性插值，最后根据1和2的值对点进行线性插值。

插值前后的三维高斯光斑曲线如图13所示。

插值后的图像变得更加的细化、平滑，对插值后的灰度光斑图像采用与插值前同样的方式求取中心，得到中心的坐标为2(59.7713，59.7919)，由式(29)可得误差2=0.1308。

由中心的坐标及1、2可以得出，对高斯光斑曲线使用二维双线性插值后，光斑的中心定位精度有了提高，但上述方法是对图像进行整体的插值，而圆拟合法的本质上是对光斑的边缘数据采集以及运用最小二乘法进行拟合，所以直接对图像边缘数据信息进行双线性插值运算，提高用于拟合的有效像素，有望进一步的提高精度。因此，首先把光斑边缘所对应的逻辑变量转化为可进行插值运算的unit8类型变量，对边缘所对应的灰度矩阵进行双线性插值，插值前后的光斑边缘成像图如图14所示。

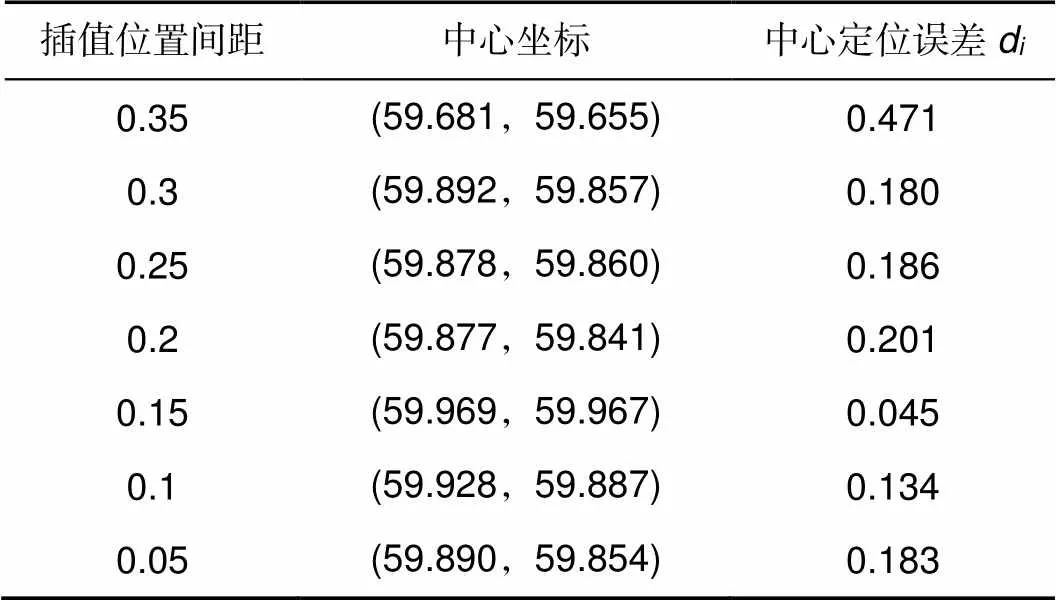
表1 中心坐标及误差

在对边缘信息进行插值时，发现插值的位置不同，最终的结果也不尽相同，当插值点离有效的信息点太远时还有可能造成中心定位精度的降低，因此对灰度矩阵有值的位置进行线性插值时要选择适当的位置，然后用圆拟合法进行处理得到中心坐标。

当插值点分别离边缘的坐标从0.35开始每次递减0.05，得到的中心坐标及误差d如表1所示。

由表1可知，插值位置离有效像素点坐标太远会造成毛刺，对于圆拟合法来说反而加入了一些无用的用于拟合的点数，从而造成更大的误差；而距离太近时，却又影响了用于拟合的真实的有效像素点。当插值位置离有效像素点位置为0.15时，此时中心定位精度最高，中心的坐标为3(59.928，59.887)，将坐标带入式(29)中得到3=0.045。将3代入式(27)中得到此时的屈光度误差仅为0.012D。

对比1、2、3的值可知，整体的插值和边缘有效位置的插值都进一步地提高了所求取中心坐标的精度值，因此采用双重双线性插值有效地提高中心坐标的精度，中心精度的提高则进一步影响了屈光度测量的精度，所以使用该方式提取中心将会有效地提高屈光度精度的测量。

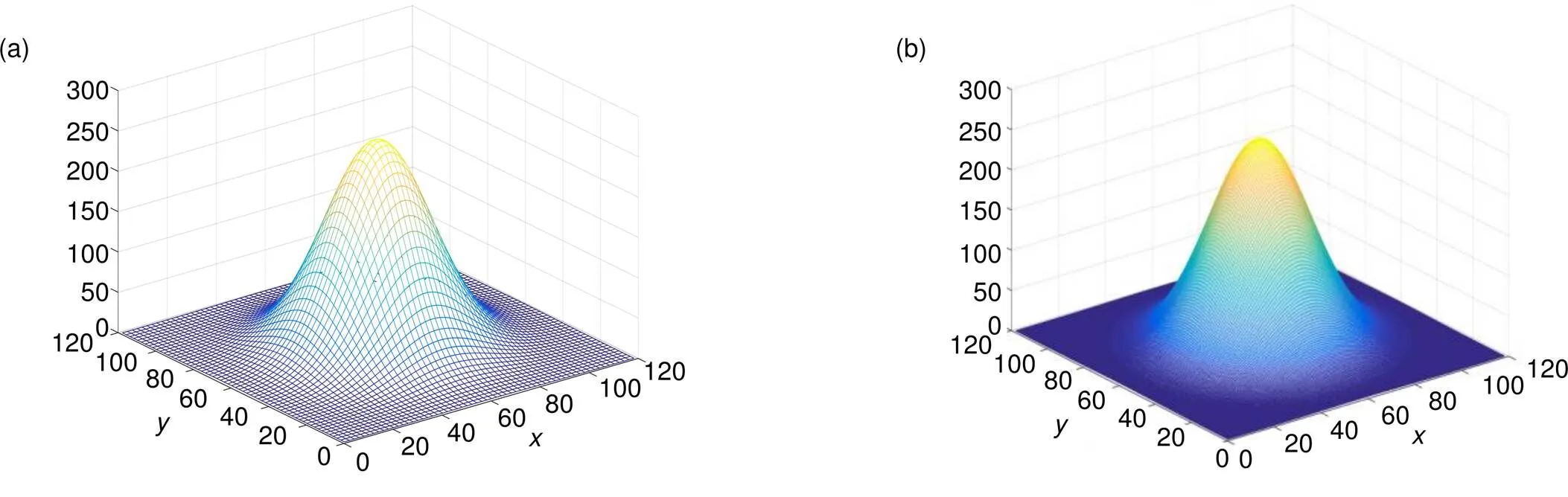
图13 (a) 插值前高斯曲面图；(b) 插值前高斯曲面图

图14 (a) 插值前的图像边缘信息图；(b) 插值后的图像边缘信息图

4 结 论

本文研究了哈特曼法测透镜屈光度的误差来源并建立了相对完善的误差模型。光源采用绿色LED光源以及忽略透镜与光电探测器之间的距离1，既免去了阿贝数的修正，同时也减少了算法的复杂性，对最终测量结果产生较小的误差。对于透镜倾斜及光轴未与透镜几何中心轴相重合而产生的误差，当角度过大时，会产生较大的屈光度误差，影响了实验结果的准确性，在实验中务必保持透镜与入射的平行光相互垂直以及光源的光轴与透镜的几何中心轴相重合，实际应用中可用本文所述误差模型来进行修正。且由于光电探测器上光斑中心的定位如果不准确则会产生较大的误差，因此可采用本文所述的圆拟合法与双重双线性插值结合起来提高光斑中心求取的准确度，确保中心定位的高精度从而保证屈光度测量结果的准确性。

[1] Mumzhiu A M, Strakun G I. Investigation of an automatic lensometer[J]., 1972, 15(4): 538–541.

[2] Cordero I. Understanding and caring for a lensmeter[J]., 2016, 29(94): 37.

[3] Barbosa E A, Silva D M, Nascimento C E,. Progressive power lens measurement by low coherence speckle interferometry[J]., 2013, 51(7): 898–906.

[4] Aono Y, Negishi M, Takano J. Development of large aperture spherical lens with glass molding[J]., 2000, 4231: 16–23.

[5] Fu X H, Dong H, Jia Z H,. Research on processing technology of odd-form off-axis aspherical lens[J]., 2014, 9281:92812F.

[6] Ceyhan U, Henning T, Fleischmann F,. Measurements of aberrations of aspherical lenses using experimental ray tracing[J]., 2011, 8082: 80821K-1.

[7] Yang B S, Liao H Y, Wang H. Error analysis and correction of digital projection focimeter[J]., 2004, 12(S1): 136–139.

杨并上, 廖海洋, 王涵. 数字投影式焦度计误差分析及校正方法[J]. 光学精密工程, 2004, 12(S1): 136–139.

[8] Zhu L Q, Zhu S L. Measuring error and correcting method of the dioptometer[J]., 2006, 27(S2): 1284–1285.

朱林泉, 朱苏磊. 焦度计的测量误差和校正方法[J]. 仪器仪表学报, 2006, 27(S2): 1284–1285.

[9] Zhao J Q, Guo Z Y, Yan J. An image processing auto lensmeter[J]., 2012, 39(3): 34–39.

赵俊奇, 郭智勇, 闫洁. 一种图像处理的全自动焦度计[J]. 光电工程, 2012, 39(3): 34–39.

[10] Shen C H. Briefing the influence of dispersion on detecting lensmeter[J]., 2010, 29(5): 534–537.

沈春花. 浅谈色散对焦度计检测的影响[J]. 北京生物医学工程, 2010, 29(5): 534–537.

[11] Snoeys W. Monolithic CMOS sensors for high energy physics[J]., 2019, 924: 51–58.

[12] Mahato S B, de Ridder J, Meynants G,. Measuring intra-pixel sensitivity variations of a CMOS image sensor[J].J, 2018, 18(7): 2722–2728.

[13] Song W T, Cheng J J, Liu Y,. Three-dimensional image authentication using binarized images in double random phase integral imaging[J]., 2019, 17(5): 21–25.

[14] Roy S, Bhattacharyya D, Bandyopadhyay S K,. An improved brain MR image binarization method as a preprocessing for abnormality detection and features extraction[J]., 2017, 11(4): 717–727.

[15] Cheng M M, Liu Y, Lin W Y,. BING: Binarized normed gradients for objectness estimation at 300fps[J]., 2019, 5(1): 3–20.

Error model analysis and correlation correction of Hartmann's focimeter

Yang Jinlong, Jia Hongzhi, Jin Tao*, Xiang Huazhong, Zhang Dawei, Zhuang Songlin

School of Optical-Electrical and Computer Engineering, University of Shanghai for Science and Technology, Shanghai 200093, China

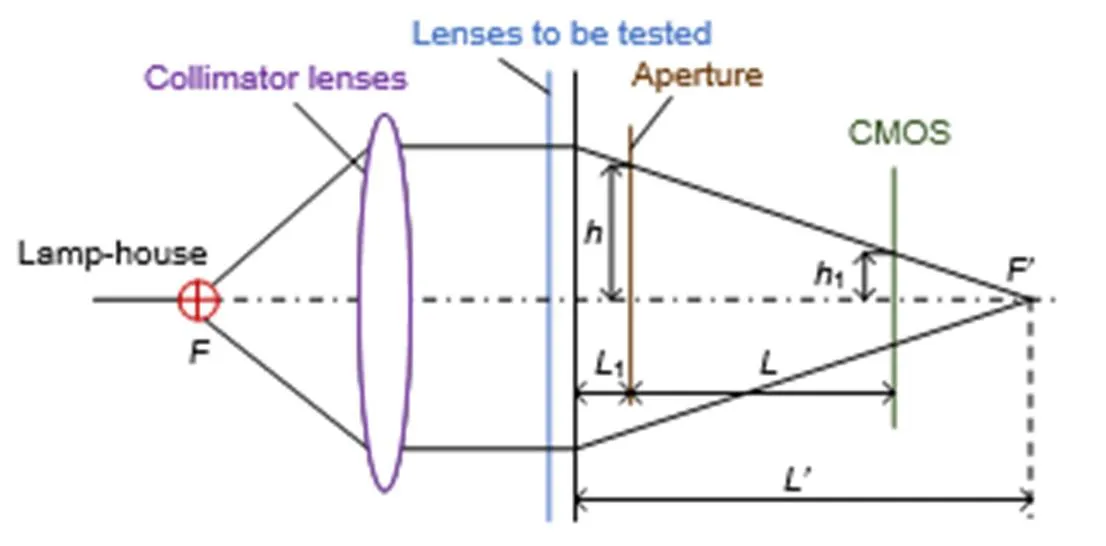
Measuring model for Hartmann method

Overview:The focus meter mainly adopts the Hartmann diaphragm measurement method.The parallel light passes through the lens and the Hartmann diaphragm plate on the photodetector image. The spot image formed without the lens has a corresponding change in position, according to the position of the spot. The change in distance calculates the optical parameters of the lens’ top power. This method can not only effectively reduce the error caused by human but also accurately measure the optical parameters of the lens. However, there is no complete error model for autofocus focal meters. Therefore, the relatively perfect error model analysis of the Hartmann measurement method is beneficial to the error correction of the subsequent focal meter measurement. The inaccuracy of the actual diopter measurement is caused by the dispersion error of the light source, the inaccurate of the photodetector’s central positing, the tilt of lens, and the misalignment between the incidence axis and the main axis of the lens. Through the analysis of the error model, the inaccurate positioning of the CMOS photodetector centroid will lead to larger errors. Therefore, a dual bilinear method is proposed. Combining the interpolation method with the fitting method, one can find the center of mass, and it’s the method is effectiveness and accuracy. The conclusion is obtained through analysis. The light source is the green LED light source. Ignoring the distance between the lens and the CMOS photodetector, the Abbe number correction can be eliminated and the complexity of the algorithm can be reduced, resulting in a small error in the final measurement result. For the errors caused by the lens tilt and the misalignment between the incidence axis and the main axis of the lens. The larger misalignment above the large diopter error, and it affects the accuracy of the experimental results. In the experiment, it is necessary to keep the lens and the incident light is perpendicular to each other. In practice, the error model described in this article can be used for correction. Moreover, if the location of the spot center of mass on the CMOS photodetector is inaccurate, a larger error will occur. Therefore, combining the fitting method in this article with the double bilinear interpolation can improve the accuracy of the spot center of mass and ensure the high positioning of the center of mass, ensuring the accuracy of the diopter measurement results.

Yang J L, Jia H Z, Jin T,Error model analysis and correlation correction of Hartmann's focimeter[J]., 2021, 48(3): 200238; DOI:10.12086/oee.2021.200238

Error model analysis and correlation correction of Hartmann's focimeter

Yang Jinlong, Jia Hongzhi, Jin Tao*, Xiang Huazhong, Zhang Dawei, Zhuang Songlin

School of Optical-Electrical and Computer Engineering, University of Shanghai for Science and Technology, Shanghai 200093, China

In order to reduce the error and improve the measurement accuracy, a more detailed error model is established for the Hartmann method of focal power measurement in this paper. It focuses on the analysis of several problems that cause the error of refraction problems, including the dispersion error of the light source, the inaccurate of the photodetector’s central positing, the tilt of lens, misalignment between incidence axis and main axis of lens, and the incident light and the lens are not perpendicular. At last, it is concluded that the inaccuracy of the center extraction on the photodetector will cause a large error to the final result. For all these reasons, a method of dual bilinear interpolation combined with a fitting method to find the centroid is proposed, proving its effectiveness and accuracy.

Hartmann diaphragm; focimeter; error model; image processing; centroid calculation

10.12086/oee.2021.200238

TN29

A

2020-06-28；

2020-09-18

杨金龙(1990-)，男，硕士研究生，主要从事焦度计与旋光仪的研究。E-mail：870015801@qq.com

金涛(1985-)，男，博士，副教授，主要从事精密测量的研究。E-mail：jintao@usst.edu.cn

* E-mail: jintao@usst.edu.cn

版权所有©2021中国科学院光电技术研究所

杨金龙，贾宏志，金涛，等. 哈特曼法焦度测量模型的误差分析及修正[J]. 光电工程，2021，48(3): 200238

Yang J L, Jia H Z, Jin T,Error model analysis and correlation correction of Hartmann's focimeter[J]., 2021, 48(3): 200238