大矢高凸柱面的超精密车削轨迹计算方法研究

雷茸粮，李 云*，林妩媚，张 帅，青建宏，唐林峰

大矢高凸柱面的超精密车削轨迹计算方法研究

雷茸粮1,2，李 云1,2*，林妩媚1,2，张 帅1,2，青建宏1,2，唐林峰3

1中国科学院光电技术研究所，四川 成都 610209；2中国科学院大学，北京 100049；3西南石油大学，四川 成都 610500

阵列微结构光学元件广泛用于各种光束匀化场合，而常规的加工方法难以满足大矢高凸柱面阵列的精度要求。本文采用超精密车削成型法，分析了影响金刚石车削的主要因素，设计了顺序搜索法和二分搜索法寻找车削轨迹，并对比了两种方法的优缺点，结合Matlab软件用二分搜索法成功找到车削轨迹及数控程序，并在超精密车床上进行了车削实验，得到了表面轮廓误差在135 nm的大矢高阵列微结构。证明了二分搜索法能够准确获得车削轨迹，并且此法可同时适用于球面轮廓和非球面轮廓，具有重要的工程应用价值。

大矢高阵列微结构；凸柱面；超精密车削；半径补偿

1 引 言

阵列微结构光学元件广泛用于激光整形，均匀照明等多种场合。它是一种基于微透镜阵列的折射型光学元件[1-2]。与衍射光学元件相比，其光能利用率更高，不会产生多级衍射现象，因而在一些高端应用场景，常被优先采用。在光刻机照明系统中，均匀照明是保证曝光线条线宽均匀一致的一项重要技术。通常，用于光刻机照明系统的匀光元件有积分棒、衍射光学元件和微透镜阵列。其中微透镜阵列出射孔径角较大，可以实现大面积照明，且匀光基于折射原理，能避免高阶衍射造成较大的能量损耗，并且能保持光的偏振特性[3-5]。

目前针对阵列微结构的加工通常采用基于曝光、显影、刻蚀等类似半导体生产的工艺。主要包括灰度掩模光刻、电子束刻蚀技术、光刻胶-熔融技术、离子交换技术等加工工艺[2,5-8]。国内外许多研究机构采用以上的加工方式都获得了不同的研究成果，如丹麦技术大学光子工程系的Chakrabarti[9]等人使用光致抗蚀剂涂覆的模具复制方法制作出了光学微透镜阵列，美国俄亥俄州立大学综合系统工程系的Zhou[10]等人利用超精密金刚石铣削的方法加工出了微透镜阵列的模具，并利用模压复制方法对红外玻璃进行模压得到了微透镜阵列，日本庆应义塾大学科学技术学院机械工程系Mukaida和Yan[11]两位学者使用慢刀伺服车削的工艺方法在单晶硅表面上实现了微透镜阵列的延性域去除超精密车削加工；中国科学院长春光学精密机械研究所史成勇[12]等利用软光刻和热形变技术在PDMS上制作出了半球形微透镜阵列，天津大学的张雄、宋乐[13]等通过单点金刚石车削对PMMA(聚甲基丙烯酸甲酯)进行加工，获得七子眼仿生复眼系统，台湾大学采用光刻掩模法及压弯法在PDMS制作曲面复眼结构模具及成型件[3]，中国科学院光电技术研究所研究团队采用光刻胶热熔法及刻蚀技术制作出大F数的微透镜阵列[2]。但在高数值孔径的光刻机中采用的柱面微结构阵列矢高大，精度高，仅仅通过曝光、显影、刻蚀等常规加工手段往往难以制造[14-16]。超精密车削技术是获得阵列微结构的一种高效方式，具有高精度、适合制作大矢高结构等特点，极具加工潜力[17-20]。超精密车削技术可以使工件的形状精度达到亚微米级，表面粗糙度达到纳米级。加工精度不受微结构矢高增大而降低，适合于阵列微结构的制作。

2 结 构

图1(a)所示是一种大矢高凸柱面的阵列微结构，其具有以下几个难点：1) 大矢高。所谓大矢高指阵列微结构最高点到最低点的距离，如图1(b)中所示，取值范围一般在100 μm以上；2) 接缝小。每个柱面结构之间采用凹缝连接，接缝距离小至几十微米，如图1(c)所示，通常需要五轴的超精密车床采用刨削的方式进行加工；3) 高面形精度。阵列微结构的面形精度要求优于200 nm，而阵列微结构一般都采用光学曲面，由于光学曲面属于复杂的几何面形，要求能够同时达到较高的表面质量和面形精度便比较困难，采用常规方法进行加工的精度低、成本高、难度大[21]。

图1 大矢高凸柱面阵列微结构。(a) 大矢高凸柱面; (b) 柱面参数; (c) 柱面接缝

图2 搜索法原理图

3 车削轨迹计算方法

对于超精密车削加工而言，刀具切削轨迹引起的误差很大程度上能够影响整个加工表面的表面质量，尤其是面形精度。因此在超精密加工中必须对刀触点轨迹进行补偿，获得刀位点轨迹，即刀具实际加工轨迹。加工中采用的金刚石刀具的刀尖并不是一个理想的点，而是具有一定半径的圆弧，因此超精密车削机床将刀尖圆弧圆心作为刀位点进行控制。

寻找刀位点轨迹的方法有两种，一种是顺序搜索法(如图2所示)，一种是二分搜索法(如图3所示)。顺序搜索法，首先将加工轮廓离散化为个点，作为刀触点P(x, z)。已知刀尖圆弧半径，刀位点Q从远处按照一定的步进距离向曲面轮廓移动。每移动一次，计算刀位点与曲面轮廓上每一个刀触点|PQ|的值，找到min|PQ|。若min|PQ|>，刀位点Q继续移动后再次计算min|PQ|值；直到min|PQ|£后，将此时的刀位点Q作为切削时刀位点坐标。这种方法的优点是只要步进距离取得足够小，寻找的切削刀位点坐标就能非常准确；缺点是精度越高，计算量越大，耗时越长，效率低。

二分搜索法同样先将轮廓离散为若干点，作为刀触点P(x, z)。已知刀尖圆弧半径，计算点刀位点Q(x, z+)和曲面轮廓上每一个刀触点(,)的距离，找到最小距离min。若min£，则将Q作为P点切削时的刀位点；若min>，则将刀位点Q(x,)移到¢(x,z+/2)作为新的刀位点Q的坐标。重复计算Q与(,)的距离，若min£，则将此时的Q作为P点切削时的刀位点；反之，则继续将Q(x,z+/2)移到²(x,z+/4)作为新的Q，再重复以上操作，直到若min£为止，此时的Q即为点切削刀位点。这种方法能够快速找到较为准确的切削刀位点，大大地减小了计算量，节约了时间。

4 车削实验及结果分析

为验证二分法寻找车削轨迹的准确性，实验以球面轮廓为例车削大矢高柱面阵列微结构。图4是生成的球面轮廓，根据二分搜索法可以生成图5中虚线所示的球面轮廓车削轨迹。在采用超精密车削时，若刀尖圆弧半径大于轮廓的最小曲率半径，就会发生干涉切削。为了避免发生干涉，刀尖圆弧半径应该满足条件[21]：

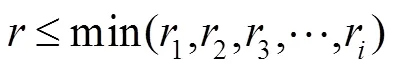
图3 二分法寻找车削轨迹。(a) 二分法原理图；(b) 二分法流程图

图4 球面轮廓图

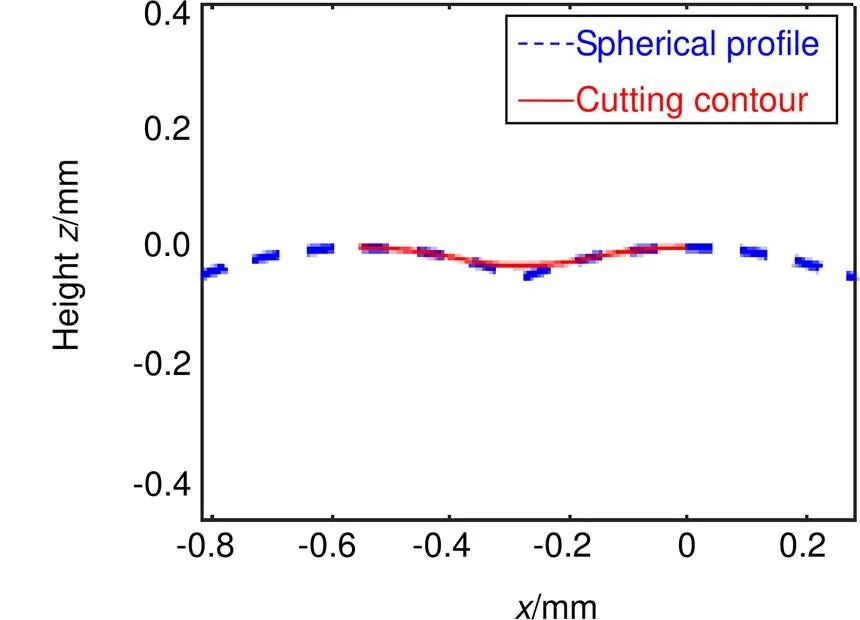
图5 二分搜索法寻找球面轮廓车削轮廓

柱面微透镜阵列为直线型排布阵列结构，车削工艺中通常需要采用精密五轴机床制作。实验室的机床是德国LT Ultra MTC400超精密车削机床，机床外形如图6所示，加工零件的面形精度在100 nm以内。受实验条件限制，本文以两轴联动超精密金刚石车床作为实验设备研究大矢高凸柱面阵列的车削技术，切削示意如图7所示。选用车削参数如表1所示。

在进行切削实验之前，先计算工件总切削深度。计算生成切削轨迹最高点和最低点之差可以求出切削深度，如图8所示。

图6 LT Ultra MTC400车床外观图

图7 切削示意图

表1 实验车削参数

图8 刀具切深

图9 球面阵列结果分析。(a) 测量原始曲线；(b) 最小二乘法拟合曲线；(c) 球面轮廓误差

切削后球面阵列结果分析如图9所示，使用台阶仪对工件进行测量，表面形貌结果如图9(a)所示。在检测过程中，由于检测平台倾斜导致检测走针轨迹与阵列微结构不垂直，因此需先对数据进行预处理。预处理的过程是截取图中一段数据进行线性拟合，利用斜率求出旋转角度，这一过程称之为“调平”。对调平后的曲线进行最小二乘法拟合，最小二乘法是常用的曲线拟合方法，在随机误差为正态分布时，通过最大似然法推算出的一个最优估计值。它可使测量误差的平方和最小，因此也被视为从一组测量值中求出一组未知量的最可信赖的方法之一。拟合后寻找曲线的半径和圆心坐标(，)，并根据圆心坐标(，)和画出拟合曲线如图9(b)所示。拟合后的圆心坐标为(0.689，-0.779)，为0.788 mm，基本达到要求半径。图9(c)为调平曲线和拟合曲线差值的绝对值曲线，根据调平曲线和拟合曲线的偏差值的标准差，得出轮廓误差为135 nm，基本上达到了该实验室超精密车削机床的切削面形精度极限值。

4 结 论

大矢高凸柱面阵列微结构是光刻机照明系统中的重要匀光元件，它形貌复杂，特征结构尺度小，矢高大，面形精度高，加工难度极大，采用常规曝光、显影的方法难以达到要求。采用超精密车削方式加工，具有诸多技术优势。本文从研究车削轨迹出发，提出采用二分搜索法计算车削轨迹，并在超精密车削机床上车削了球面柱面阵列微结构，获得了精确的面形。该方法适用于球面、非球面等多种轮廓曲线，并且能够快速寻找最优车削轨迹，对进一步研究五轴超精密机床加工大矢高阵列微结构提供了理论基础，具有重要的工程应用价值。

[1] Fan Z B. Research on key technology in ultra-precision turning processing of microstructure on cylindrical surface[D]. Changsha: National University of Defense Technology, 2014.

范占斌. 圆柱表面微结构超精密加工关键技术研究[D]. 长沙: 国防科学技术大学, 2014.

[2] Liu X, Zhang M, Shi L F,. Fabrication method for the microlens array of high-number[J]., 2017, 46(2): 0222004.

刘鑫, 张满, 史立芳, 等. 一种大数微透镜阵列的制备方法[J]. 光子学报, 2017, 46(2): 0222004.

[3] Xu L W. Research on ultra-precision turning technology of microlens array[D]. Harbin: Harbin Institute of Technology, 2015.

徐礼威. 微透镜阵列超精密切削加工技术研究[D]. 哈尔滨: 哈尔滨工业大学, 2015.

[4] Tian F, Liu X L, Zhang X D,. Influence of manufacture error on optical performance of micro lens array[J]., 2016, 36(2): 0222002.

田霏, 刘现磊, 张效栋, 等. 微透镜阵列加工误差对光学性能的影响[J]. 光学学报, 2016, 36(2): 0222002.

[5] Xiao Y F, Zhu J, Yang B X,. Design of micro-cylindrical-lens array used for illumination uniformization in lithography systems[J]., 2013, 40(2): 0216001.

肖艳芬, 朱菁, 杨宝喜, 等. 用于光刻机照明均匀化的微柱面镜阵列设计[J]. 中国激光, 2013, 40(2): 0216001.

[6] Wang H, Dong L H, Zhu G D,. Fabrication method of quartz aspheric microlens array for turning mask[J]., 2018, 45(4): 170671.

王灏, 董连和, 朱国栋, 等. 车削掩模的石英非球面微透镜阵列制作方法[J]. 光电工程, 2018, 45(4): 170671.

[7] Zhang W G, Dong X C, Du C L. Microlens array imaging-based photolithography technique[J]., 2010, 39(3): 469–472.

张为国, 董小春, 杜春雷. 微透镜列阵成像光刻技术[J]. 红外与激光工程, 2010, 39(3): 469–472.

[8] Shi L F, Ye Y T, Deng Q L,. Method to fabricate artificial compound eye[J]., 2013, 42(9): 2462–2466.

史立芳, 叶玉堂, 邓启凌, 等. 制备人工复眼结构的方法[J]. 红外与激光工程, 2013, 42(9): 2462–2466.

[9] Chakrabarti M, Dam-Hansen C, Stubager J,. Replication of optical microlens array using photoresist coated molds[J]., 2016, 24(9): 9528–9540.

[10] Zhou W C, Zhang L, Yi A Y. Design and fabrication of a compound-eye system using precision molded chalcogenide glass freeform microlens arrays[J]., 2018, 171: 294–303.

[11] Mukaida M, Yan J W. Ductile machining of single-crystal silicon for microlens arrays by ultraprecision diamond turning using a slow tool servo[J]., 2017, 115: 2–4.

[12] Shi C Y. Research on the design and image process of bioinspired spherical compound eve imaging system[D]. Changchun: University of Chinese Academy of Sciences (Changchun Institute of Optics, Fine Mechanics and Physics, Chinese Academy of Sciences), 2017.

史成勇. 仿生曲面复眼系统设计及其图像处理研究[D]. 长春: 中国科学院大学(中国科学院长春光学精密机械与物理研究所), 2017.

[13] Zhang X, Song L, Zhang S S,. The method for the calibration and measurement of bionic compound-eye system[J]., 2014, 41(3): 35–42.

张雄, 宋乐, 张姗姗, 等. 仿生复眼系统标定及测量方法研究[J]. 光电工程, 2014, 41(3): 35–42.

[14] Li R B, Du X, Zhang Z H,. Ultra-precision machining of optical microstructures[J]., 2003, 1(1): 57–61.

李荣彬, 杜雪, 张志辉, 等. 光学微结构的超精密加工技术[J]. 纳米技术与精密工程, 2003, 1(1): 57–61.

[15] Zhu D C. Technology study and accuracy analysis of optical microstructures manufactured by fast tool servo[D]. Changsha: National University of Defense Technology, 2010.

朱登超. 光学微结构快速车削工艺研究与精度分析[D]. 长沙: 国防科学技术大学, 2010.

[16] Zhang X D, Wang Z C, Zeng Z,. Optimized design of sine-transition cutting path for microlens array in ultra-precision cutting[J]., 2017, 15(4): 239–245.

张效栋, 王志诚, 曾臻, 等. 微透镜阵列超精密切削正弦过渡路径优化设计[J]. 纳米技术与精密工程, 2017, 15(4): 239–245.

[17] Huang K T, Fang F Z, Gong H. Effect of surface microscopic topology generated by ultra-precision turning on optical characteristics[J]., 2013, 21(1): 101–107.

黄昆涛, 房丰洲, 宫虎. 超精密车削表面微观形貌对光学特性的影响[J]. 光学精密工程, 2013, 21(1): 101–107.

[18] He C K, Zhang P, Li D,. Research on influencing factors and development trend of surface quality in ultra precision turning[J]., 2017(11): 12–15.

何成奎, 张平, 李东, 等. 超精密车削表面质量影响因素及发展趋势研究[J]. 装备制造技术, 2017(11): 12–15.

[19] Zhang X D, Fang F Z, Cheng Y. Optimized design of cutting path for freeform surface in ultra-precision turning[J]., 2009, 42(3): 278–282.

张效栋, 房丰洲, 程颖. 自由曲面超精密车削加工路径优化设计[J]. 天津大学学报, 2009, 42(3): 278–282.

[20] Wang Y, Yu J C. Compensation for error of diamond tool's cutting edge in single diamond turning[J]., 2011, 38(1): 98–102.

王毅, 余景池. 超精密车削金刚石刀具刃口误差的高精度补偿[J]. 光电工程, 2011, 38(1): 98–102.

[21] Yu H J. Theoretical and technological research on optical freeform surface of single point diamond ultra-precision turning[D]. Changchun: Jilin University, 2015.

于慧娟. 光学自由曲面单点金刚石超精密车削理论与技术研究[D]. 长春: 吉林大学, 2015.

Research on the calculation method of the ultra-precision turning trajectory of large-vector high-convex cylinders

Lei Rongliang1,2, Li Yun1,2*, Lin Wumei1,2, Zhang Shuai1,2, Qing Jianhong1,2, Tang Linfeng3

1Institute of Optics and Electronics, Chinese Academy of Sciences, Chengdu, Sichuan 610209, China;2University of Chinese Academy of Sciences, Beijing 100049, China;3Southwest Petroleum University, Chengdu, Sichuan 610500, China

Schematic diagram of dichotomy

Overview:Array microstructured optical elements are widely used in various beam homogenization occasions, with complex structures and extremely high surface shape accuracy requirements. The microstructures of large-sag high-convex cylindrical arrays have the characteristics of high sagittal height, large diameter, small seam, and high surface shape accuracy. It is often difficult for conventional processing methods to meet the accuracy requirements. As a ultra-precision turning forming method, the diamond tip has a micron-level structure, and the processing accuracy is not limited by the height of the microstructure, which is a very potential method for processing the microstructure of the large array of high convex cylindrical arrays.

How to ensure the machining accuracy is an important problem that needs to be solved in ultra-precision turning. This paper analyzes the main factors that affect diamond turning-turning trajectories. Increasing the turning trajectory accuracy can improve the turning surface accuracy and obtain a good machining surface shape. This article analyzes and compares two methods, namely sequential search method and binary search method, to find the best turning trajectory, and each method has its own advantages and disadvantages. The sequential search method can obtain a high-precision turning trajectory, but the calculation amount will gradually increase as the stepping distance decreases, which leads to lower efficiency. The binary search method can quickly obtain the turning trajectory, and the calculation amount is relatively small. So the calculation time is short, which greatly improves the turning efficiency. Combined with actual production applications, improving efficiency is one of the important issues that need to be considered. Therefore, this paper chooses the binary search method to find the turning contour trajectory.

The binary search method can be used to find the turning trajectories of both spherical and aspherical contours. Combined with laboratory conditions, the experiment took the spherical contour as an example, and the spherical turning trajectory was successfully generated through numerical control programs. Furthermore, turning experiments on ultra-precision turning machine tools were carried out, with the turning results being analyzed using the least square method. The original curve is compared with the fitted curve, and the difference curve is obtained. It is found that the contour error of the workpiece after processing is 135 nm, and the expected surface shape and good surface contour error are basically obtained. This article provides a theoretical basis for how to find the turning trajectory of the large-vector convex cylindrical array microstructure, and has important practical application value.

Lei R L, Li Y, Lin W M,Research on the calculation method of the ultra-precision turning trajectory of large-vector high-convex cylinders[J]., 2021, 48(3): 200192; DOI:10.12086/oee.2021.200192

Research on the calculation method of the ultra-precision turning trajectory of large-vector high-convex cylinders

Lei Rongliang1,2, Li Yun1,2*, Lin Wumei1,2, Zhang Shuai1,2, Qing Jianhong1,2, Tang Linfeng3

1Institute of Optics and Electronics, Chinese Academy of Sciences, Chengdu, Sichuan 610209, China;2University of Chinese Academy of Sciences, Beijing 100049, China;3Southwest Petroleum University, Chengdu, Sichuan 610500, China

Array microstructure optical elements are widely used in various beam homogenization occasions, but conventional processing methods cannot meet the accuracy requirements of large-sagittal convex cylindrical arrays. In this paper, the ultra-precision turning forming method is used to analyze the main factors affecting diamond turning, the sequential search method and the binary search method are designed to find the turning track, and the advantages and disadvantages of the two methods are compared. Furthermore, the binary search method is successfully found by combining the Matlab software turning trajectory and the numerical control program. As proof-of-concept demonstrations, turning experiments are carried on an ultra-precision lathe, and a large-vector high-array microstructure with a surface profile error of 135 nm is obtained. It proves that the force binary search method can accurately obtain the turning trajectory, and this method can be applied to both spherical and aspherical contours, showing important engineering application value.Keywords: large-vector high-array microstructure; convex cylindrical surface; ultra-precision turning; radius compensation

10.12086/oee.2021.200192

O439

A

2020-05-28；

2020-09-24作者简介：雷茸粮(1995-)，女，硕士研究生，主要从事仪器仪表工程的研究。E-mail：1414601822@qq.com

李云(1986-)，男，博士，副研究员，主要从事精密制造的研究。E-mail：liyun@ioe.ac.cn

* E-mail: liyun@ioe.ac.cn

版权所有©2021中国科学院光电技术研究所

雷茸粮，李云，林妩媚，等. 大矢高凸柱面的超精密车削轨迹计算方法研究[J]. 光电工程，2021，48(3): 200192

Lei R L, Li Y, Lin W M, et al. Research on the calculation method of the ultra-precision turning trajectory of large-vector high-convex cylinders[J]. Opto-Electron Eng, 2021, 48(3): 200192