一种改进A*算法在智能车中的应用研究
杨 瑶,付克昌,蒋 涛,刘甲甲,向泽波,程永杰
(1.成都信息工程大学 控制工程学院,成都 610225;2.中国科学技术大学 软件学院,合肥 230000)
随着硬件设备的升级,将智能驾驶技术运用到普通汽车上的可能性逐渐增加。而在未来汽车的发展中,路径规划技术不仅将作为智能驾驶技术中的重要组成部分,也将是智能车发展中不可缺少的部分[1]。到目前为止,针对路径规划技术的研究,国内外众多学者做了大量贡献,其中主要包括:采用模板树的RRT算法[2];将栅格邻域扩展到无限个的A*算法[3];通过限制障碍物范围的改进APF[4]和使用信息素的蚁群算法[5]等。其中,A*算法由于能在无向图中寻找最优路径,因此被广泛用于解决其他规划问题[6]。但是,传统A*算法将移动载体看作质点处理,导致了所生成的路径不平滑[7]和路径点与障碍物距离过近的问题[8]。此外,因为本研究的智能车存在阿克曼转向约束,所以不能仅简单地当作质点考虑[9]。为了解决传统A*算法因为载体不同所带来的问题,通过建立智能车运动学模型,获得智能车的约束条件,将该约束与启发函数相融合,使得扩展节点更准确。具体过程为:首先通过加入方向代价解决车辆在起始时刻路径转折角度大于车辆最大转向角的问题,然后使用自适应障碍物惩罚代价,自动调节路径点与障碍物之间的距离。最后,将车辆约束条件与改进A*算法的转折点相结合,并使用自由边界三次样条插值算法拟合转折点获得更优路径。通过对传统A*算法进行上述改进后,可使所生成的路径更平滑。
1 基于阿克曼转向的运动学模型
由于车辆不具有完整性约束,因此本文中只建立了简易的运动学模型。以野马新能源电动车为实验的载体(如图1所示),在标准惯性系下,用智能车后轴中心表示车体坐标(x,y),轴距用L=1.56 m表示,车宽为D,车辆航向角为θ。同时,本实验室平台最大转向角为40°,转向角用φ。此外,实验平台最大转折曲率和最小转弯半径分别为0.16 m-1和8 m,曲率和转弯半径用K和R表示。只考虑智能车在二维平面运动[10],并认为在行驶的过程中无俯仰和侧倾。因此,智能车运动的瞬间应满足式(1)和(2):
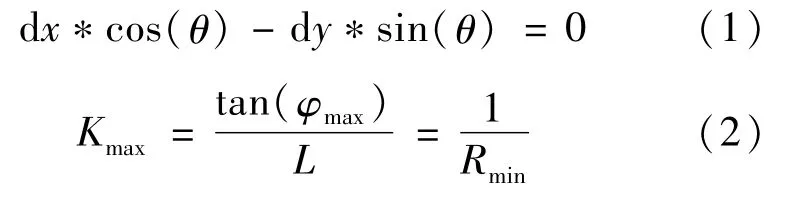

图1 基于野马E70电动汽车改造的智能车驾驶平台

图2 车辆简化运动学模型示意图
2 A*算法
在进行栅格地图的路径搜索时,最常用的规划算法是使用启发式搜索的A*算法,该算法也是处理其他规划问题的常用算法之一。A*算法的评价函数为:
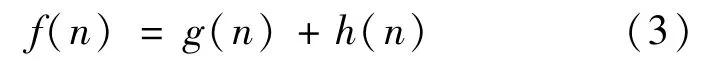
式中:f(n)表示节点n的总代价;g(n)表示起点到当前n的实际路径长度代价;h(n)表示启发估计路径长度代价。
A*算法的基本步骤如下:
步骤1初始化:获得起点坐标Start和终点坐标Goal,并定义开启列表(OpenList)和关闭列表(CloseList)。
步骤2将Start插入OpenList中,并判断OpenList是否为空。如果为空,则规划失败。否则,执行步骤3。
步骤3根据OpenList中所有节点代价值的大小,更新OpenList中节点的代价值,并选取最小代价值的当前节点(CurrentNode)。判断Current-Node是否为Goal。如果是,规划成功,反向形成路径。否则,执行步骤4。
步骤4扩展CurrentNode的周围节点(NeighborNode),并将CurrentNode从OpenList中删除,加入到CloseList中。
步骤5判断NeighborNode是否为障碍物。如果是,则加入CloseList,并返回步骤3。否则,判断NeighborNode是否在OpenList。如果是,则更新NeighborNode代价值大小。否则该节点还未被扩展过,重新计算NeighborNode代价值,并插入到OpenList,并执行步骤3。
在传统A*算法的启发代价中大多使用曼哈顿距离和欧式距离来估计当前节点到目标点的近似距离,往往使得估计值不合理。同时,传统A*算法在执行的过程中未能考虑智能车运动特性,使得生成路径不能很好地被底层控制模块实现。因此,本文中针对传统A*算法的上述问题进行改进。
3 改进A*算法
由于传统A*算法所针对的移动载体不是智能车,因此所生成的路径不能满足智能车的运动学特性。为了优化传统A*算法,本文采用连续曲线取代传统A*算法用曼哈顿距离或欧氏距离估计到目标点的方式,提出方向代价和自适应障碍物惩罚代价方法解决所生成的路径不满足车辆运动学的问题。然后,使用智能车的最大前轮转角约束优化转折点。最后,用自由边界三次样条插值算法对优化后的转折点进行插值,使路径更为平滑。
改进A*算法中的估价函数定义为

式中:o(n)是车辆的方向代价;a(n)是起始点到扩展节点n的角度代价;d(n)是起始点到扩展节点n的直线代价;c(n)是扩展节点n到障碍物的惩罚代价;A是角度代价的系数;nangle是起始点的朝向与起始点到扩展节点n所形成的夹角之差;B是直线代价的系数;dnode是起始点到扩展节点的距离。由于加入方向代价主要是解决车辆初始时刻路径转折角度较大的问题,所以o(n)使用单调递增的函数;dth为扩展节点到起始点距离的阈值;d为扩展节点到障碍物的距离。
3.1 对函数h(n)进行改进
在A*算法中,用于估计节点n的启发代价值h(n)决定着A*算法对其他节点的扩展速度及所扩展节点是否合理。假定当前节点到达终点的实际最小代价为H(n)。当h(n)大于H(n)时,A*算法遍历的节点最少,算法运行速度快,但是很难获得最优路径;当h(n)等于H(n)时,为A*算法最理想的时候,所规划出的路径最短,算法运行速度最快;当h(n)小于H(n)时,A*算法所计算的节点数目最多,算法运行速度较慢,但是此时能够生成较优的路径[19]。同时,曼哈顿距离和欧式距离是常被用于A*算法启发代价h(n)的计算,但往往造成所计算的距离过大或过小。因此,本文中提出使用曲率连续函数对当前节点的代价值进行较为合理的估值。
首先,通过连接起始点和目标点来判断路径上是否有障碍物,生成预判函数yh=k*x+b(yh中x取值从起始点到终点)。如果没有障碍物,则说明直线运动的代价最小,则使用y=k*x+b作为启发函数h(n),用于计算路径点的代价值。否则,使用二次函数y=a*x2+b*x+c计算扩展节点启发函数h(n)的代价值。如令扩展节点为p(n)=(x1,y1),终点q=(x2,y2),则:

式中yh为预判函数。
当预判函数yh在起始点和终点间没有障碍物且车辆的朝向和直线的夹角φ2>φmax时,最优的路经应该是1条曲线,就需要对启发函数y=k*x+b进行修改,即使用二次函数对扩展节点的代价值进行估计。因为在规划前只知道起始点和终点的坐标不能拟合二次函数,所以通过设置2个点来进行拟合。设起始点终点是q=(x2,y2)(将起始点s设为坐标原点,便于后续处理)。
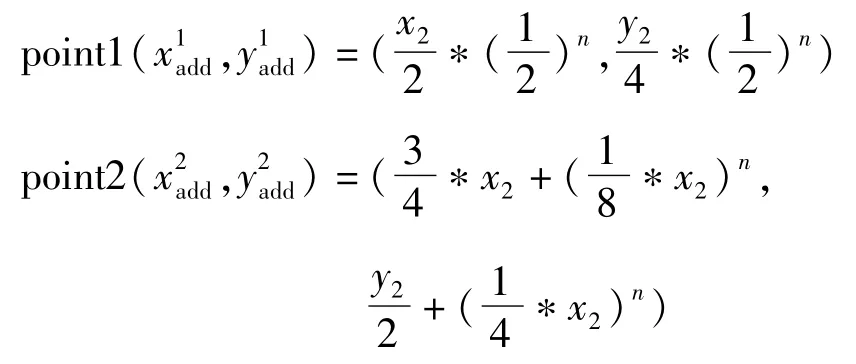
式中n<N,n从0开始。
n是point1和point2遇到障碍物的次数的迭代次数。如果point1和point2中有1个点为障碍物,则n+1并重新计算新的point1和point2。N是最多迭代的次数。当的坐标与起始点终点q=(x2,y2)的坐标的x或y相同或n>N时,则使用yn(n)=k*x1+b来估计扩展节点的代价值。如果所预置的点并不在障碍物中,则使用起始点和终点q=(x2,y2),拟合一条曲线y1(x)=a1*x2+b1*x+c1,替换原本的yh(n)=k*x1+b。
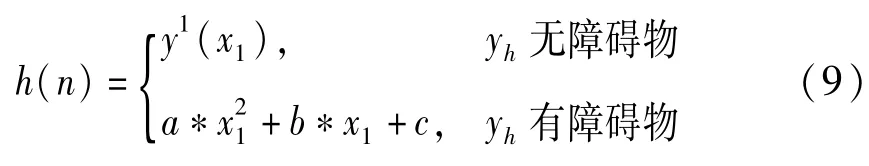
图3、4分别是采用传统A*算法的曼哈顿距离和本文改进启发函数所规划的路径。从图中可看出:与传统的A*算法相比,改进的启发函数所规划的路径更加平滑,转折次数更少,路径更短。
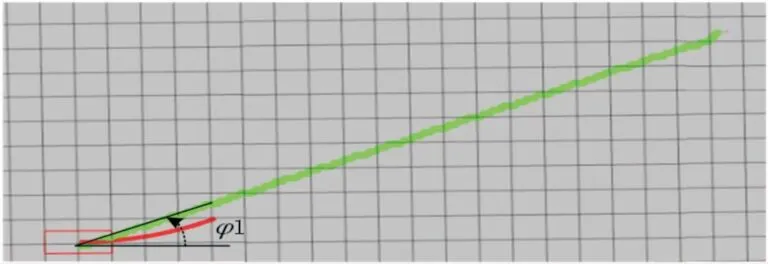
图4 改进A*算法所规划的路径示意图
当预判函数yh与车身初始航向的夹角大于φmax且在yh中x取值在起始点到终点之间无障碍时,根据车辆的运动学特性可知:最优路径应为一条曲率连续的弧线。因此,用二次曲线y1(x)代替yh(n)对当前节点进行估值。所规划的路径如图5所示,能够很好满足车辆的运动学特性。
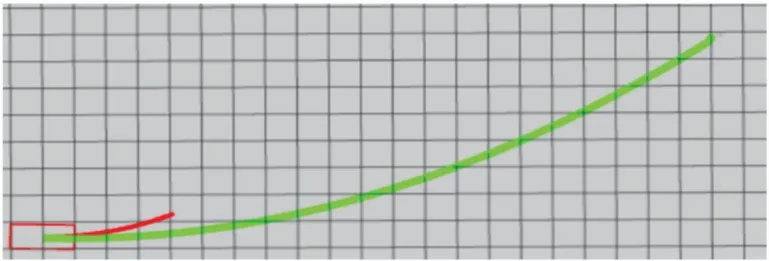
图5 改进h(n)所规划的路径
3.2 方向代价o(n)
通过对图2中车辆运动学的建模分析,可知车辆在运动过程中存在着最大转角。而在传统的A*算法中未考虑车辆的最大转角和车辆的朝向,因此规划出的路径在起始的时刻存在着不合理的情况,导致智能车不能很好地跟踪所规划的路径。为解决上述问题,本文在传统A*算法基础上提出方向代价,将车辆朝向和车辆最大转角考虑到估价函数中,从而解决传统A*算法不能处理车辆运动学的问题。
优化步骤如下:
步骤1获得车辆的实际朝向(本文设正东方向为零度,逆时针为正)。
步骤2如果扩展节点到起始点的距离dnode大于dth,则将方向代价赋值为零。否则,将计算扩展节点与起始点的夹角和距离并代入式(5)(6)中。
通过对比图6、7可看出:加入方向代价后,能够较好地解决初始时刻规划不合理的问题。同时,也能够减少50%以上的扩展节点数。
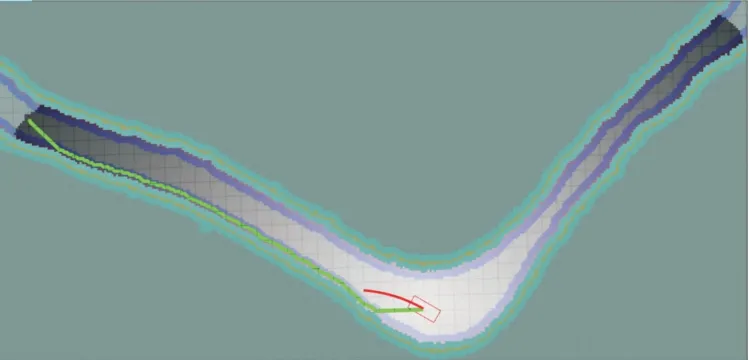
图6 未加方向代价的路径点示意图
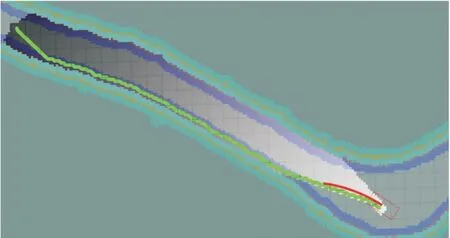
图7 加入方向代价的路径点示意图
3.3 自适应障碍物惩罚代价c(n)
传统的A*算法主要是应用于全向移动机器人和差速移动机器人等,因此在规划模块使用A*算法生成路径时,常常将运动载体当成质点处理。但是,由于智能车体积较大,因此在规划过程中,不能简单将智能车看作质点处理。此外,因为定位模块和地图模块存在误差,所以需要路径规划模块所规划产生的路径要与障碍物形成一定的安全距离。为了获得安全距离,马飞等[8]通过在A*算法上加入铲运机的形状作为约束条件,并使用9个轮廓特征点表示铲运机外形形状,同时,将该项约束条件命名为碰撞威胁代价,通过在扩展节点上加入该打分代价进而获得安全距离。但是,在每个扩展节点加入9个轮廓特征点降低了算法的效率。因此,本文通过判断扩展节点p(n)=(x1,y1)四周距离的障碍物检测点(图8)是否有障碍物来对c(n)进行赋值。如果有,则将障碍物威胁代价赋为无穷大,否则赋为零。同时,由于道路宽度不一致,导致阈值D不能很好地被设置,所以提出自适应障碍物惩罚代价。通过判断智能车与障碍物的距离是否合理,自动调整阈值D进行重规划。通过这样的方式能够较大地提高A*算法的运行效率,避免手动调参。

图8 障碍物监测点示意图
为了测试本文中的惩罚代价,参照文献[8]的方法,在智能车的简化模型上加入碰撞检测点(如图9所示)。同时,采用文献[8]的方法对扩展节点进行打分判断,并在图10的测试点上进行测试分析(L1表示车长,D表示车宽)。

图9 智能车简化模型的碰撞检测点示意图

图10 惩罚代价和典型的惩罚代价的测试点示意图
在图10中的坐标点为所测试的起始点和目标点,其中S表示起始点,分别选取G1,G2,G3,G4,G5作为目标点。
图11为使用本文惩罚代价与典型惩罚代价在图10的测试结果对比。通过图11(a)可知:在保证规划路径与障碍物形成安全距离的前提下,使用本文障碍物惩罚代价与采用典型惩罚代价,所生成的路径长度并无明显的差距。但是,由图11(b)可知:典型惩罚代价使用的时间比自适应障碍物惩罚代价所用的时间更多。此外,通过图11(a)和(b)可知:随着A*算法所规划距离增加,采用典型惩罚代价的时间增幅比本文的惩罚代价更大,因此本文的方法在长距离规划中优势更为明显。
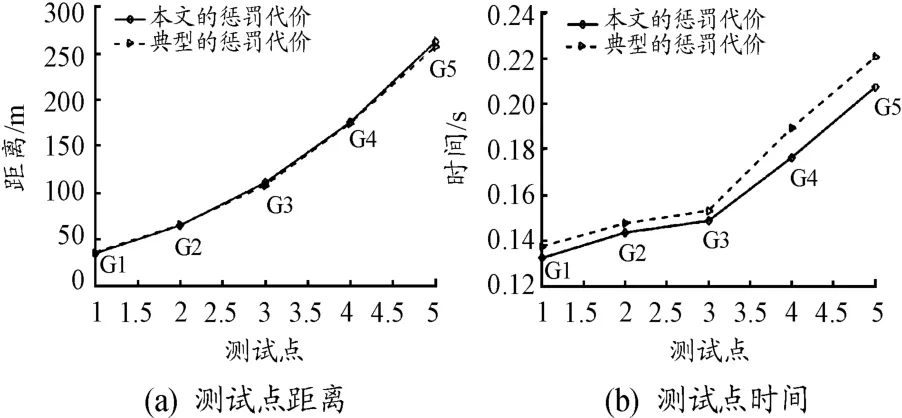
图11 2种不同的方法在测试点的测试曲线
本文中优化步骤如下:
步骤1判断扩展节点四周的障碍物检测点是否为障碍物。
步骤2如果是,则在扩展节点上增加障碍物标志位。否则,执行步骤3。
步骤3判断扩展节点是否为目标点。如果否,则执行步骤一。如果是则扩展到目标点,判断CloseList中的节点四周是否有障碍物标志位。如果有,则减小阈值D,进行重新规划,直到阈值D小于零。否则,从CloseList中输出路径。
通过对比图12(a)和(c)可知,加入自适应障碍物惩罚代价的A*算法所规划的路径与障碍物保持一定距离,使得车辆在行驶过程中更加安全。同时,由于图9中道路最窄处为2.8 m,将阈值设置为D=1.6 m导致所规划的路径贴合路沿(如图12(b)所示),不能被智能车所执行。在CloseList中形成路径时,判断节点存在着障碍物标志位,所以降低阈值D重新规划(如图12(c)所示),得到使用于智能车的路径。

图12 3种路径结果示意图
改进A*算法流程如图13所示。
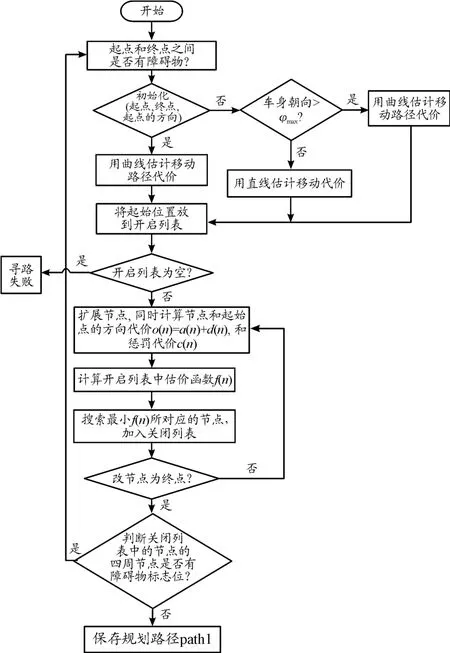
图13 改进A*算法流程框图
3.4 路径优化
因为智能车存在阿克曼转向约束,所以导致智能车有最大转向角的限制。为了解决该限制,本文将车辆最大转角约束与改进A*算法规划的路径相结合,具体实现步骤如下:
步骤1获得转折点:去掉改进A*算法所生成路径中的冗余点[11],得到转折路径点(path1)。
步骤2在路径点(path1)中依次获得3个路径点pose[i-2],pose[i-1],pose[i]将其拟合为二次曲线y(x)1=a*x2+b*x+c。如果转折点中有目标点,则将转折点添加到路径点path2中,同时完成优化转折点的过程。否则,在曲线y(x)1上的路径点到障碍物距离都大于D/2的时,执行步骤3。如果路径点与障碍物之间的距离都小于D/2,则重新执行步骤2。
步骤3判断转折点形成的角度φmax是否满足式(10),如果满足,则执行步骤2,否则执行步骤4。
步骤4将中间的转折点向曲线y(x)1开口方向移动一个栅格,如图14的B·点所示。再将代入式(10)中,判断是否成立。如果成立,重新执行步骤2并将转折点添加到path2,否则执行步骤4(图15)。

indexnew是移动后节点的索引,index是此刻节点的索引。
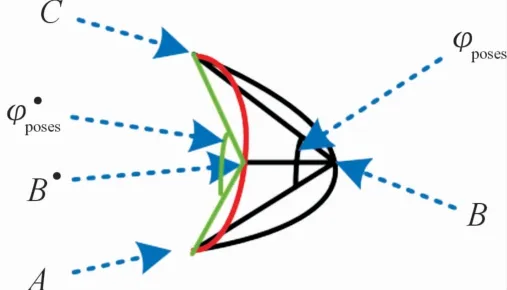
图14 转折点移动示意图
A,B,C为转折点;B·为移动后的转折点;黑色曲线为转折移动之前所拟合的曲线;红色曲线为移动之后所拟合的曲线;φposes为A,B,C所形成的角度,为A,B·,C所形成的角度。
3.5 自由边界三次样条插值算法
为了使所规划路径更为平滑,将改进A*算法的路径进行平滑处理。其中,平滑算法所得的曲线如图16所示,粉红色的数据点代表改进A*算法的转折点,使用蓝色、绿色和红色分别表示三次样条拟合、三次多项式拟合和自由边界三次样条插值算法。因为结合车辆运动学规律,车辆应尽可能走直线,只是在转变方向的地方形成符合车辆运动学的曲线,而三次样条曲线在第1个点和第2点之间产生一个曲线弧度,所以不是最优的。此外,从第6个点到第7个点,三次多项式拟合的变化斜率比自由边界三次样条插值的变化斜率大。因此,相比三次样条拟合和三次多项式拟合,自由边界三次样条插值算法较优。
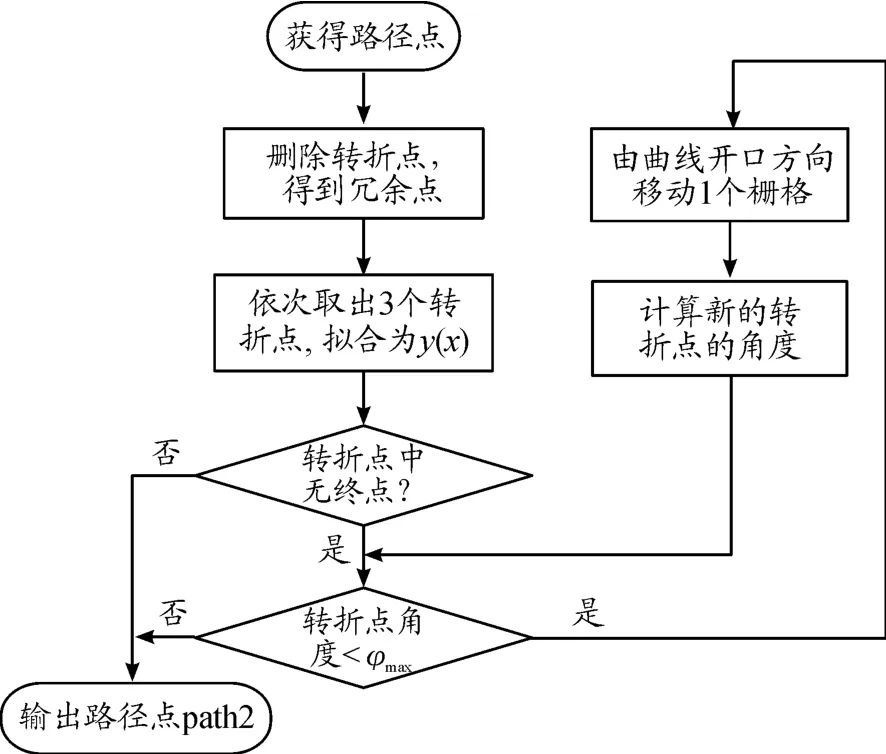
图15 路径后优化流程框图
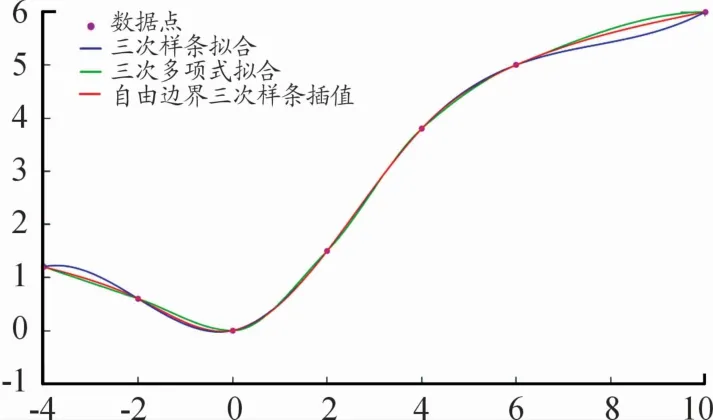
图16 平滑算法所得曲线
由于智能车在实际的行驶过程中车辆的速度和加速度都是连续的,而高次多项式计算较为复杂。所以本文使用1阶导数连续和二节导数连续的优化方法就能满足需求。通过图16的分析研究发现,自由边界三次样条插值较优。因此本文使用自由边界三次样条插值算法使曲线在衔接点处连续和光滑,且避免了高次拟合算法所带来的龙格现象[12-13]。假设S1=(x1,y1),S2=(x2,y2)和S3=(x3,y3)是path2的3个路径点。式(13)使用(S1,S2)2个拟合点,式(14)使用(S2,S3)2个拟合点。
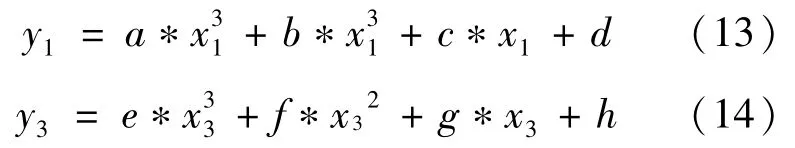
由于2点曲线都经过S2=(x2,y2),则可得式(15)
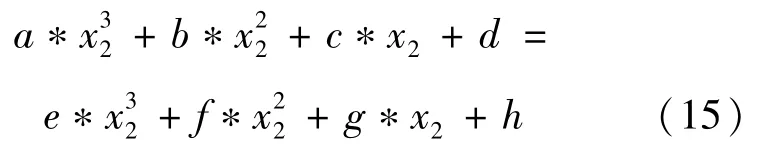
由于样条曲线衔接处的1阶导数和2阶导数连续,则可得式(16)~(18)
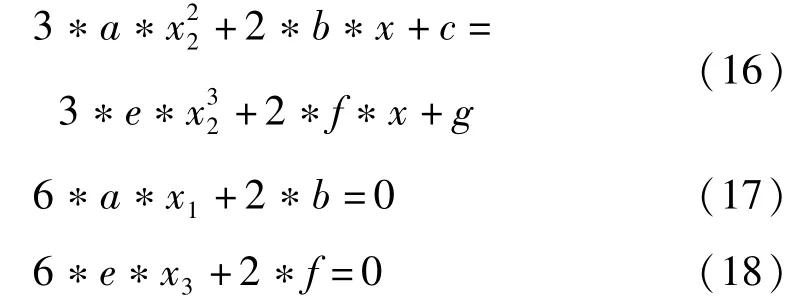
通过综合式(13)~(18)确定2条3次样条曲线的系数,用于对转折点进行拟合得到路径点。
4 算法验证
为了测试传统A*算法和本文中所提出的改进A*算法之间的优劣,将上述算法进行对比测试。同时,本实验测试使用的地图为课题组制作的学校校园地图,该地图长有4 846个栅格、宽有2 816个栅格,地图的栅格大小为0.298 m,并且本课题将坐标原点定义在校园地图的左下角。校园栅格地图见图17。此外,本课题研究采用ROS系统作为测试软件平台,并通过3D可视化工具RVIZ用于显示。使用曼哈顿距离的传统A*算法和改进A*算法在学校的栅格地图上进行仿真测试。其测试结果主要通过算法所规划路径的距离、路径的平滑性和规划所用的时间、与障碍物的距离等指标来进行判断。
为了更好地验证改进A*算法的实用性,在测试地图上选取2处连续转弯的测试区域1和2进行测试,分别使用传统A*算法和改进A*算法规划行驶路径。其中,如图18、19分别为传统算法和改进算法在2处区域中所规划的路径。最后,本文中对比的测试指标如表1所示。
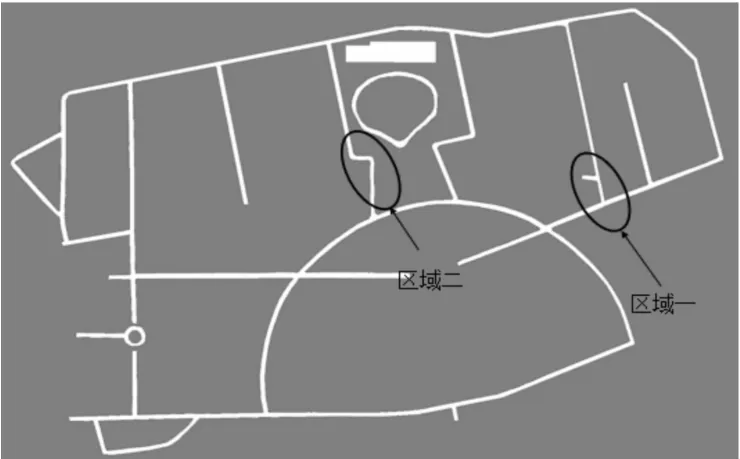
图17 校园栅格地图
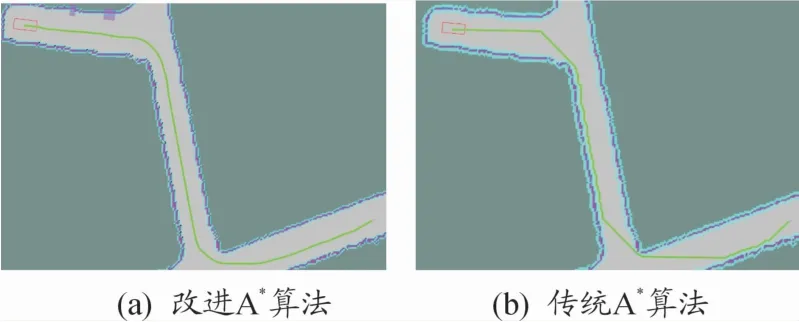
图18 区域1规化
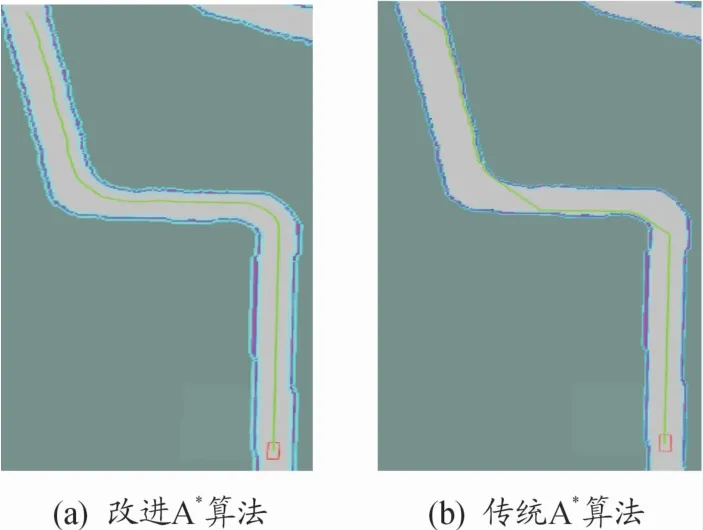
图19 区域2规化
通过对比在区域1和区域1的测试结果(a)和(b)可以看出:相比传统A*算法而言,改进A*算法生成的路径更为平滑,满足车辆的运动特性,所规划路径更为安全、可靠。同时,通过传统A*算法在区域1和区域2的规划结果能够看出该算法存在起始时刻路径不合理,规划出的路径存在着某些路径点与障碍物过近及所生成路径较为曲折等诸多问题。为了解决传统A*算法带来的问题,在传统A*算法上加入自适应障碍物惩罚代价,方向代价并将车辆约束与转折点相结合以能够较好地解决传统A*算法所带来的问题(如图18(a)和19(a)所示)。最后,通过对2种算法进行对比分析,可知改进A*算法能有效改善传统A*算法未考虑车辆运动学特性的问题。改进A*算法和传统A*算法规化结果见表1。
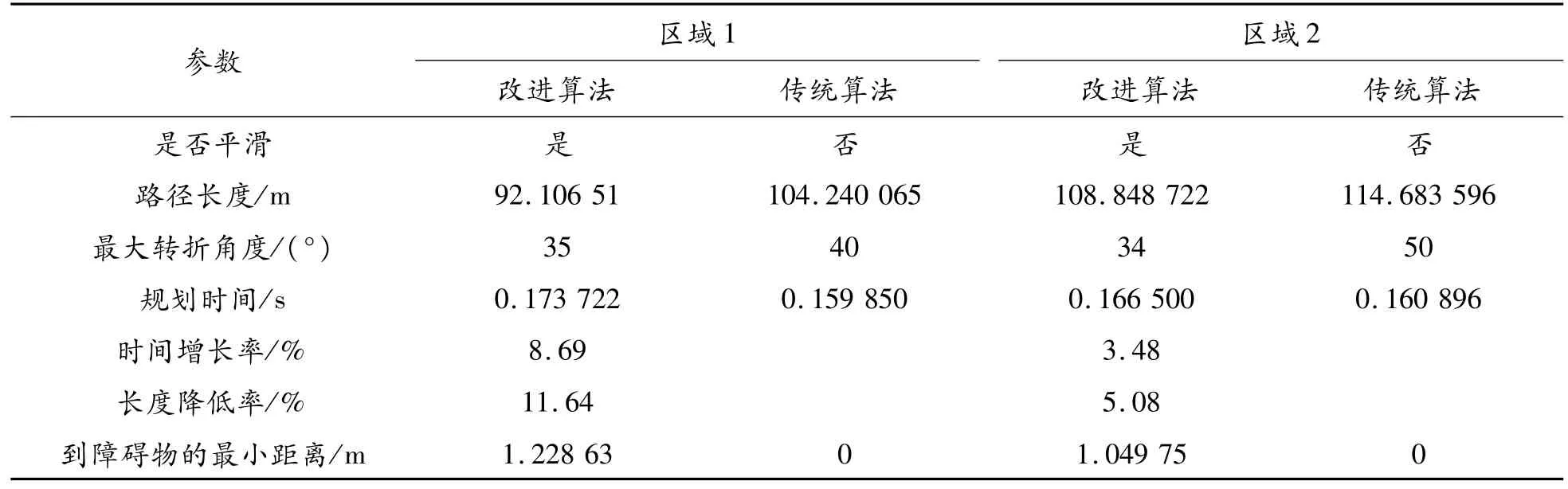
表1 改进A*算法和传统A*算法规化结果
由表1能够看出改进A*算法虽然在运行时间方面比传统A*算法略长,但是所增加的时间也在可接受的范围内。通过牺牲少量运行时间获得了更加平滑、安全,路径长度更短的路径,这样的做法是可以被接受的。
5 结论
由于传统A*算法存在着路径点与障碍物距离过近,路径转折次数较多,初始时刻路径不合理和未结合车辆运动学特性的问题。因此,本研究针对这些问题本文对其进行改进,主要贡献如下:
1)对智能车进行运动学分析,并建立其运动模型,从而获得车辆约束条件,再将约束条件代入A*算法的代价函数中使得对节点的估计值更能满足实际需求。
2)利用方向代价解决车辆起始时路径转折角度不合理的问题。
3)为了解决传统A*算法所规划的路径点与障碍物过近的问题,通过提出自适应障碍物惩罚代价判断估计点代价值是否合理,从而调整障碍物检测点的范围,进行重新规划。
4)将车辆约束条件与路径转折点相结合并使用自由边界3次样条插值拟合使得路径点更平滑,使之更好地被用于智能车的路径规划。

