基于MPC算法的车辆自适应巡航系统分层控制研究

刘 西，明 朗，胡远志

（重庆理工大学 汽车零部件先进制造技术教育部重点实验室，重庆 400054）

作为先进驾驶员辅助系统（advanced driver assistance systems，ADAS）的重要组成部分，汽车自适应巡航系统（adaptive cruise control，ACC）［1-2］能够帮助驾驶员实现自动调节节气门开度或制动压力。它不仅大大减轻了驾驶员的驾驶负担，对于减少驾驶员操作失误、提高汽车行驶安全性也具有重要意义［3］。

目前，国内外学者对ACC控制系统的研究已取得一定成果。Yi K等［4］基于线性最优理论，提出了一种应用于车辆起停巡航系统的控制算法。Bleek［5］使用模糊预测控制方法设计了一种具有自适应巡航功能的全速ACC控制器。张鹏飞［6］通过改进的LQR距离控制算法和PI速度控制算法，实现车辆的ACC功能，并降低了车辆加减速时的瞬时冲击度，提高了行驶舒适性。张丽［7］基于二次型最优化和模型预测控制理论，提出一种控制车辆纵向运动的方法，并设计出全速自适应巡航控制策略。高晓猛等［8］基于模糊控制理论，将速度误差、加速度、车间时距误差以及车间时距变化率作为输入设计了巡航控制器，通过仿真验证了控制方法的有效性。

学者们大多采用分工况控制或分层控制实现车辆ACC功能。分工况控制下，行驶工况的变化将导致控制状态变量的不连续性，进而导致控制精准性下降［9］。采用分层控制不仅能够避免不同工况间的切换问题，而且可将特定的控制目标在彼此独立的层次中分别解决，降低控制器的开发难度，提高系统鲁棒性［10］。

针对上诉问题，基于分层控制理论设计了一种车辆自适应巡航控制器：上层控制器根据前方是否有车辆行驶分别计算出巡航或跟车工况下的期望加速度值；下层控制器则根据期望加速度值向车辆的节气门或制动系统发出控制指令，最后仿真验证了控制器的正确性，并分析了仿真结果。

1 车辆自适应巡航系统设计

本文中所设计的车辆自适应巡航控制器由上层和下层控制器组成，其控制系统如图1所示。上层控制器为决策层，根据是否探测到前车划分为车距控制和速度控制2种模式，2种模式均采用模型预测控制（model predictive control，MPC）计算车辆期望加速度；计算得到的期望加速度发送到下层控制器（执行层），由油门刹车控制逻辑判定是否加速或减速，经过车辆纵向逆动力学模型计算得到对应节气门开度或制动力，最终实现车辆的加减速或车距保持，进而实现自适应巡航功能。

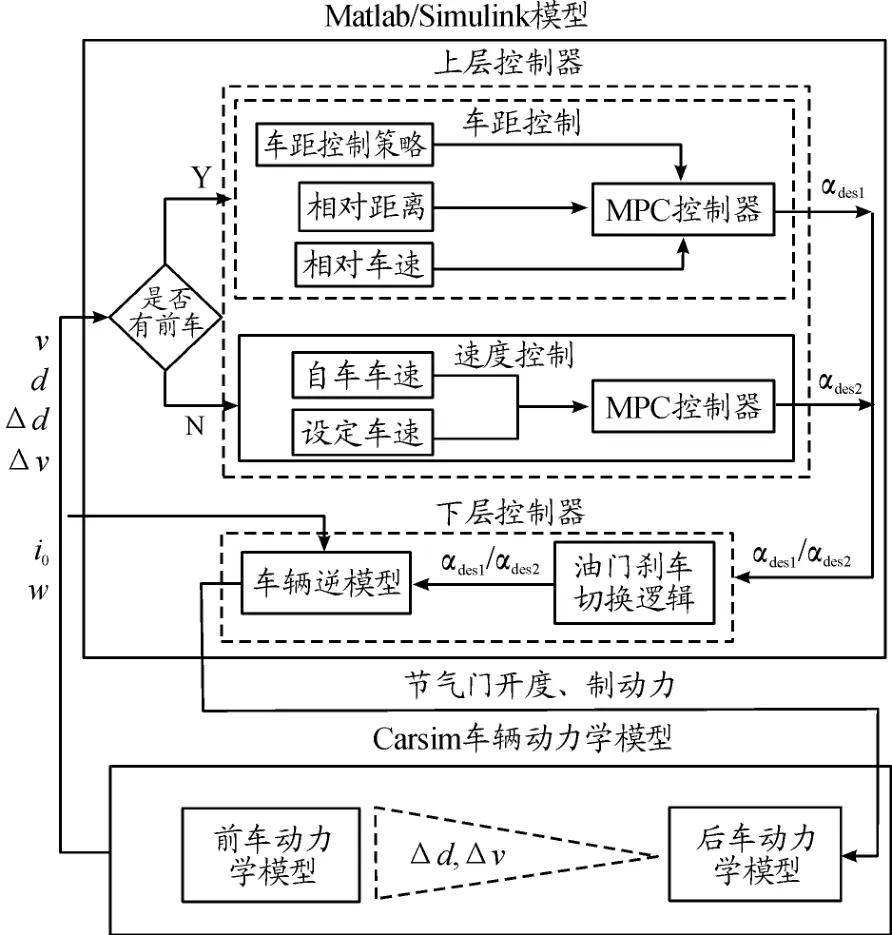
图1 车辆自适应巡航控制系统框图

1.1 上层控制器设计

1.1.1 车间距控制策略

车间距控制策略决定了车辆行驶过程中的期望跟车距离，目前应用较为广泛的2种方法中［11-12］，一种为固定车间时距（constant time headway，CTH），该方法采用固定的时距计算跟车距离：

式中：ddes为期望距离；τ为设定的固定时距值；v为本车车速；d0为最小安全距离。

由于固定的车间时距无法适应前车速度变化的复杂工况，本文中采取另一种考虑前车速度以及前车加速度变化的可变车间时距［13］（variable time headway，VTH），表达式如下：

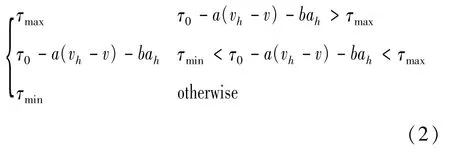
式中：τ0为默认时距，为定值；a和b为常数；vh和ah表示前车速度和加速度；tmin和tmax为设定的最小车间时距和最大车间时距，本文中分别设定为2.0 s和1.2 s。

1.1.2 兼顾多目标因素的MPC控制器

基于模型预测控制算法（MPC）设计自适应巡航系统车距控制器，通过图2对建立的状态方程进行表述。

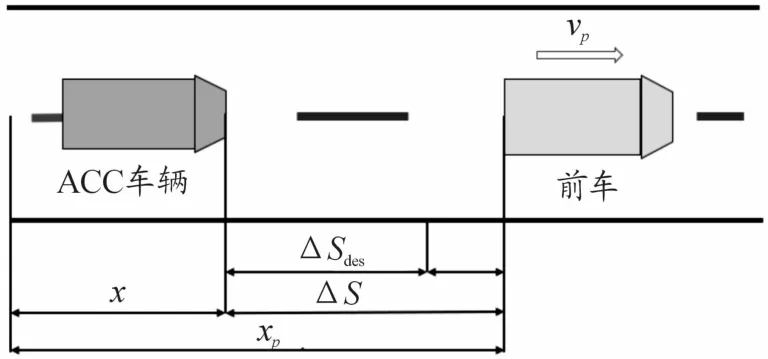
图2 车距控制纵向运动学示意图

图2中vp为前车车速；ΔS是两车实际车间距；ΔSdes是期望车间距；δ是实际车间距和期望车间距的误差；xp是前车位值；x是本车位置，根据纵向动力学有

其中：Sp为实际跟车距离；ΔS0为初始车间距。

将车辆的加速度以及加速度变化率离散化。同时，考虑前车的加速度对ACC控制车辆的影响。状态方程的输入包括本车的车速、车间距、加速度、加速度变化率以及两车的相对速度，表示为：

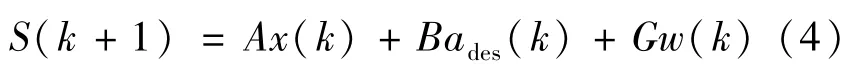
其中S（k）＝［Δx（k），v（k），vrel（k），a（k），j（k）］Τ为状态变量，状态变量中vrel为相对速度；G表示扰动变量即前车加速度的系数矩阵。

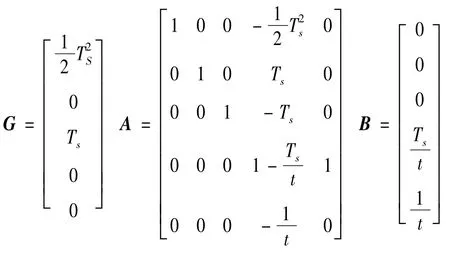
其中，Ts为计算步长，同时为了保证车辆行驶过程中的安全性，定义车距硬约束dc：

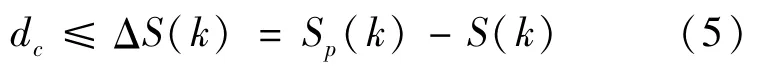
跟车过程中，为保证跟车效率，应尽快达到与前车相同车速，同时车间距保持在期望范围，即在时间k→∞时，有 δ（k）→0，vrel（k）→0。

为保证车辆行驶过程中的舒适性，在加减速过程中，车辆加速度和加速度变化率应尽量小［9］，固对车辆的加速度以及加速度变化率je进行硬约束。考虑车辆自身性能，对车辆速度、加速度、加速度变化率进行硬约束，即vmin≤v（k）≤vmax，amin≤a（k）≤amax，jmin≤j（k）≤jmax，选取间距误差（δ）、相对车速（v）、本车加速度（a）和本车加速度变化率（j）作为优化和约束目标组成系统输出向量，得系统输出方程：

利用模型预测解决这样的多目标约束，离散化的线性MPC标准方程为：

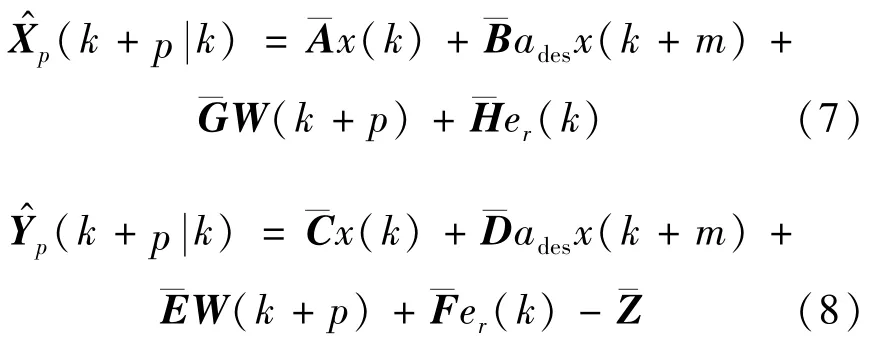
模型还需要在k时刻对未来p个时刻的扰动向量（即前车加速度）做p个时刻的预测。实际上无法在第k个时刻得到下一个时刻的前车加速度，因为计算步长通常较小，所以可以通过利用上一个时刻的相对速度和本车加速度计算以代替得到上一个时刻的前车加速度，即：

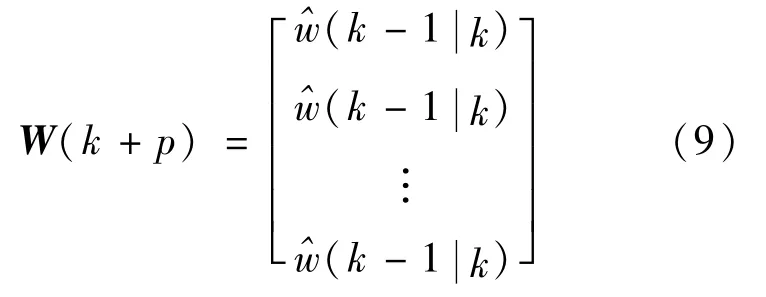
通过对迭代过程中状态方程的输出量和控制量以加权的形式转化多目标优化问题为二次规划题：

其中：Q是输出量的权重矩阵，定义为Q＝diag（qδ，qv，qa，qj）；R是控制量的权重系数。权衡跟车间距误差、相对速度、本车加速度、加速度变化率四者之间的权重关系。通过调试和对比，分别取它们的权重系数为0.6、3.5、2、2。将目标函数展开，消除与控制量无关的项化简函数得：

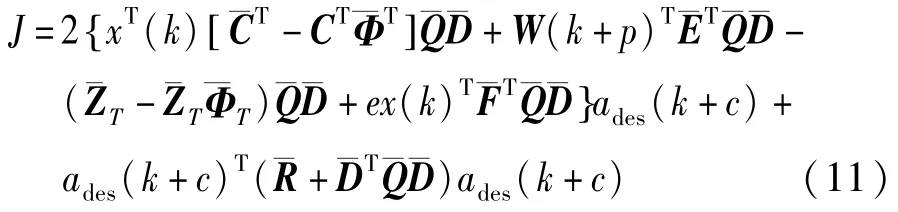
参数和条件：

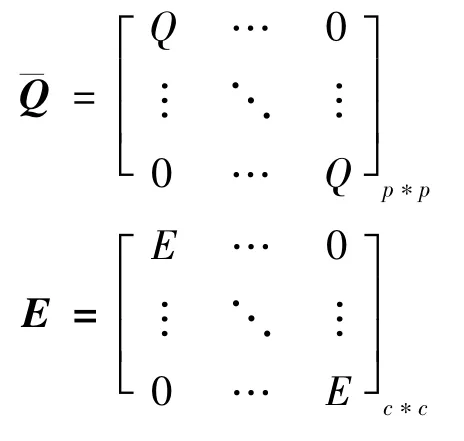
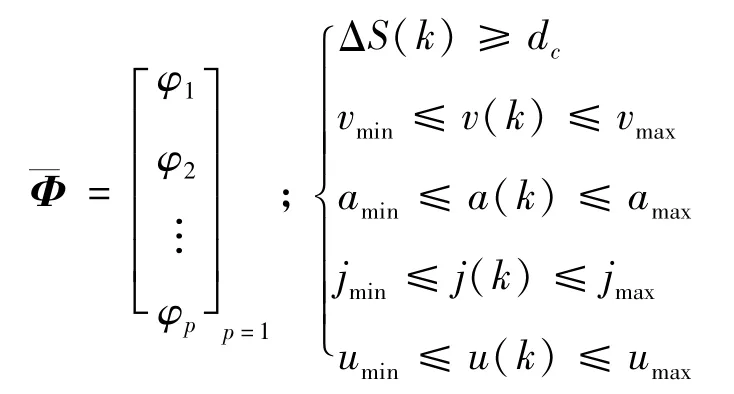
最终通过求解二次规划问题，得到每个时刻的期望加速度值。

巡航模式下的车速控制在车距控制的基础上，设置实际车距始终等于期望车距，即 ΔS＝ΔSdes，前车速度则等于设置的巡航速度，即vp＝vset，可以抽象地认为有1辆速度为设定巡航速度的汽车在匀速行驶，如图3所示。车距控制与车速控制2种模式之间的切换根据传感器是否检测到前车实现。

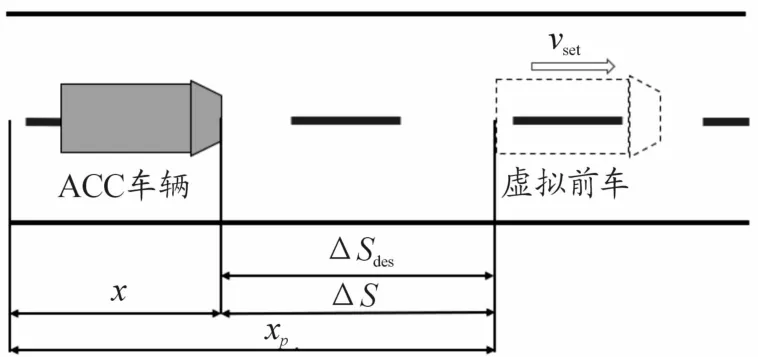
图3 车速控制纵向运动学示意图

1.2 下层控制器的搭建

由上层控制器计算得到的车辆期望加速度，位于下层的车辆逆纵向动力学模型则将加速度值通过查表的方式转换为对应的发动机节气门开度或制动力矩，然后输入到车辆动力学模型，以此对车辆进行加速、减速、匀速控制，进而实现自适应巡航功能。

1.2.1 Carsim车辆动力学模型

在Carsim车辆动力学模型软件中选用1辆C级两厢轿车，其发动机功率125 kW，匹配1个7速自动变速器。表1为搭建逆向动力学模型所采用的部分车辆参数。

在仿真过程中，Carsim车辆动力学模型需要实时输出到Simulink的车辆信息有变速器传动比（Rgear_Tr）、发动机转速（AV_Eng），加速度（Ax），车辆纵向速度（Vx）。此外，上层控制器还需要传感器采集到的相对距离（DisS1_1）和相对速度（SpdS1_1）数据。

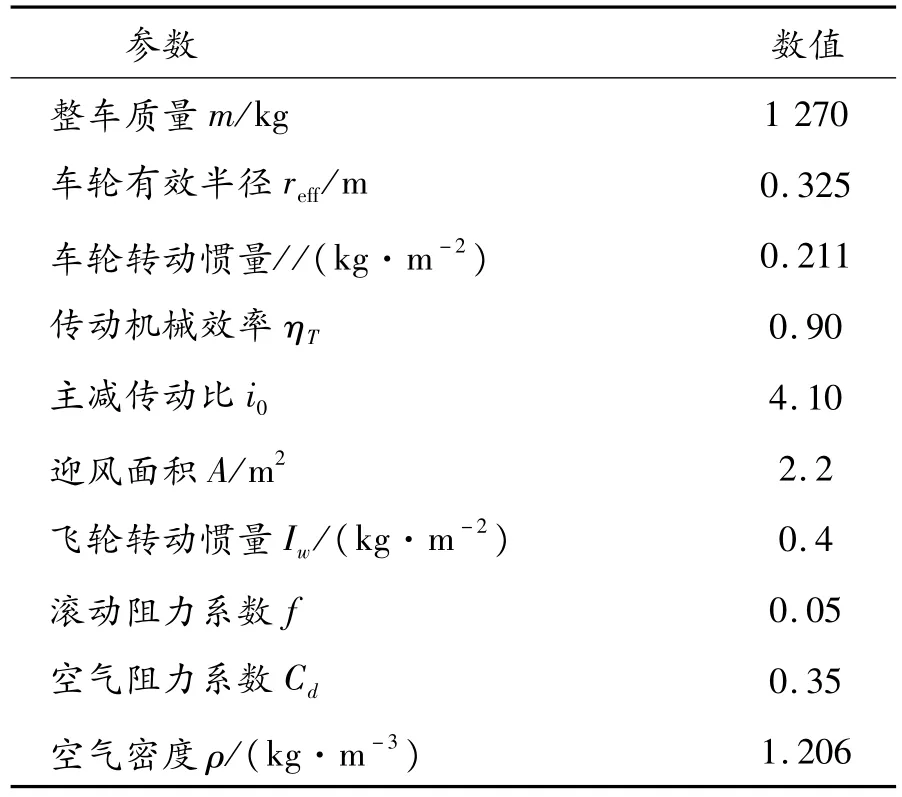
表1 Carsim车辆部分参数

1.2.2 加速控制

ACC系统主要控制车辆的纵向运动，根据汽车驱动行驶方程［14］：

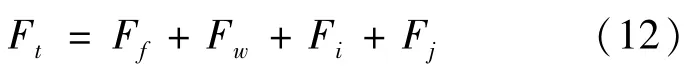
其中：Ft表示驱动力；Ff、Fw、Fi、Fj为车辆在行驶过程中需要克服的各类阻力。如果将式（12）展开：

式中：Ttq为发动机输出转矩；ηT为传动系机械效率；igio为传动系传动比；reff为车辆有效半径；f为滚动阻力系数；α为路面与水平面夹角；CD为空气阻力系数；m是整车质量；vα为车速；ρ表示空气密度；A是整车迎风面积；δ是旋转质量换算系数，计算公式如下：

当车辆在坡度为0的直线公路上行驶，即cosα＝1，sinα＝0，此时驱动方程则表示为：

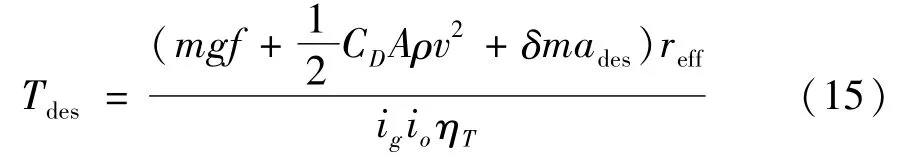
由此推理出可以根据车辆期望加速度ades计算得到发动机期望转矩Tdes。

根据车辆发动机的map图，可以反求得到发动机转矩、转速与节气门开度之间的对应关系；在Carsim软件中，提取出发动机map图数据，根据该数据构造出逆发动机模型，如图4所示。

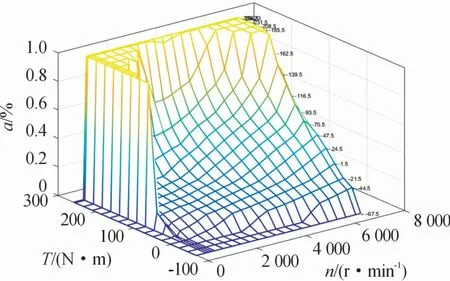
图4 逆发动机map图

通过求得的逆向发动机map图数据构造发动机逆模型，进而求出相对应的期望节气门开度αthr，如式（16）所示。

式中：αthr表示期望的节气门开度；Tdes表示期望的发动机扭矩；ω表示当前时刻的发动机转速；f（Tdes，ω）表示逆发动机扭矩特性曲线。在Simulink中通过二维查询表来建立发动机逆扭矩特性曲线，以此查询出期望的节气门开度。

1.2.3 制动控制

制动力矩大小的确定同样根据行驶方程推导，有：

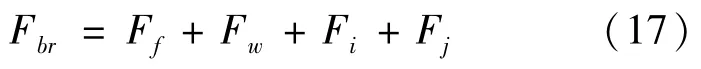
式中Fbr是作用在车轮上的制动力之和，展开得：

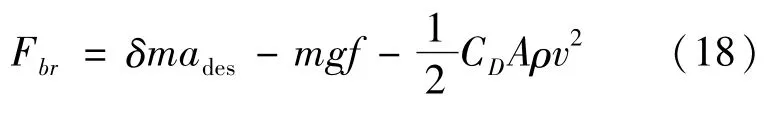
在路面最大制动力范围内，车辆所受制动压力和制动力间关系为

式中K表示制动力与制动压力的固定比值，在Carsim中给车辆输入固定的制动压力仿真即可确定K＝1 817。结合式（18）和（19），可以得到制动压力与期望制动减速度之间的关系：

1.2.4 油门／制动控制切换

在车辆正常行驶过程中，不可能同时踩下油门和刹车踏板。启动发动机后，在不踩油门踏板的情况下，车辆会处于怠速状态，此时会有一定的节气门开度；车辆需要减速的时候，首先可以利用空气阻力和滚动阻力等形式减速，如果这种情况不能满足减速需求，则踩下制动踏板增大车辆减速度。为避免车辆在行驶过程中频繁的加减速切换，保证一定的行驶舒适性，在Carsim软件中设置车辆在松开油门和制动踏板的状态下，速度从120 km／h带挡滑行减速，直到车辆稳定在一挡怠速状态，以此获得车辆加速度曲线［15］。再以此曲线为基准设定大小为0.01 g的门限值，进而得到驱动／制动逻辑曲线，如图5所示。加速度在分界线之下采取制动控制，分界线之上采取驱动模式。

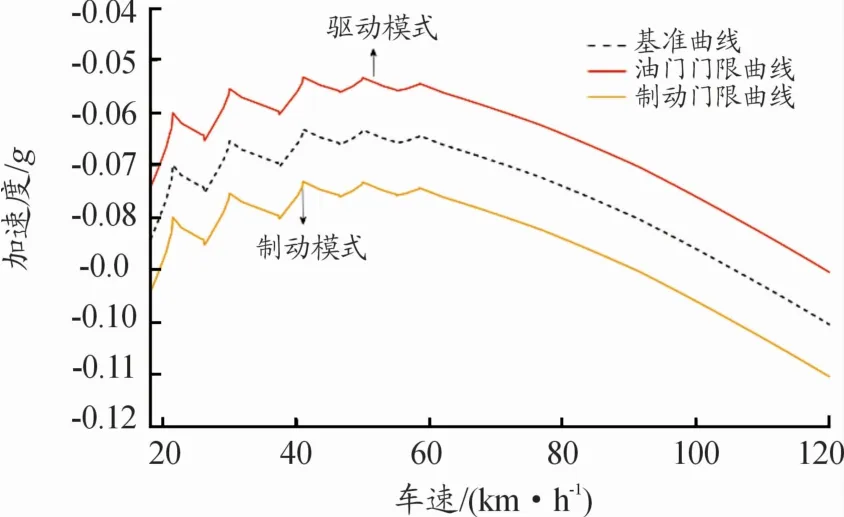
图5 油门和制动切换逻辑曲线

2 行驶工况仿真验证

设定2种典型测试工况对所搭建的车辆ACC控制器进行仿真验证。工况1在无前车的情况下设定了2个时间段的不同巡航车速，测试控制器对速度控制的稳定性和精准性以及是否能够响应巡航速度的变化；工况2引入1辆速度不断变化的前方车辆，设计1个包含诸多工况类别的组合工况，对控制器进行综合测试。

2.1 定速巡航工况

自适应巡航车辆检测到前方无其他机动车辆，此时处于速度控制模式，设置车辆初速度为30 km／h，目标巡航车速为70 km／h，45 s后巡航车速增加到100 km／h，仿真结果如图6所示。

图6 定速巡航工况仿真结果

由图6的仿真结果可以看出：自适应巡航车辆20 s后达到70 km／h的设定车速，车速超调量约为2.1%；在45 s巡航速度提高到100 km／h后，控制器响应较快，速度迅速提高，约10 s后达到设定的巡航速度，超调量约为1.3%。另外，加速度曲线中出现了几处峰值跳动，经过分析是由于车辆换挡，传动比发生瞬时变化造成。因为加速度只是发生瞬时小幅度的变化，且没有超出设定范围，所以对乘员的舒适性影响较小。

2.2 综合行驶工况

为了构造包含巡航、巡航-跟车、跟车加速、跟车减速等多种工况类别的综合工况，对自适应巡航汽车的速度控制和距离控制进行综合验证：在Carsim中添加前车，并设置与自车的初始距离为120 m，开始以60 km／h匀速行驶，33 s后开始逐渐加速，10 s速度达到90 km／h，再经过2次降速-匀速阶段，最后于85 s开始制动直至车辆停止；设置自车的初始速度为60 km／h，定速巡航速度为90 km／h。仿真结果如图7所示。

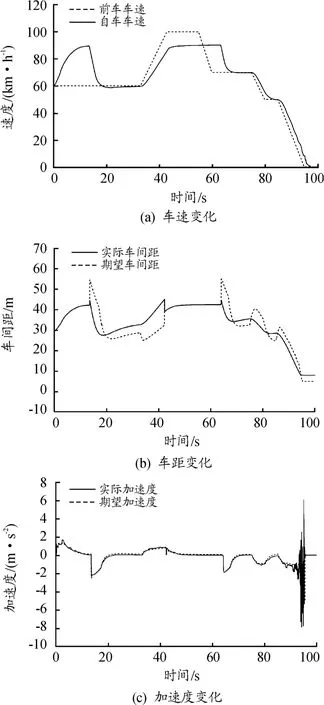
图7 巡航-跟车综合工况仿真结果

由图7可以看出：在1～10 s时，因为两车相距较远，自车并没有检测到前车，故判断为巡航行驶且自车能够正常巡航；经过约3 s巡航行驶后，自车检测到前车，此时实际车间距小于期望车间距（传感器能够探测的最大距离为45 m），所以自车开始减速；达到期望距离后，自车能够较好地跟车行驶；跟车行驶大约16 s，前车开始急加速到100 km／h，后车同样加速，因为设定的巡航速度为90 km／h，自车达到该速度后正常巡航行驶并无超域现象发生；自车巡航约20 s，两车间距逐渐拉开，直至63 s时，自车再次检测到已经减速到70 km／h的前车，此时为了达到期望间距，自车正常减速并再次跟车行驶，并保证较好的跟车效率；跟车行驶到85 s，前车紧急制动时，自车能够采取紧急制动，最终跟随前车停止且两车保持约7.5 m间距，避免了碰撞，说明控制系统对紧急制动工况具有较好适应性。整个行驶过程，实际加速度对期望加速度跟踪较好，且保持在设定的加速度区间，保证了行驶过程中的舒适性。在最后的制动停车阶段出现抖动，经过分析是由于车辆速度较低发生微小抖动造成，但因为此时车速较低，对乘员舒适性的影响有限。

3 结论

基于MPC控制算法，通过分层控制原理设计了车辆自适应巡航系统控制器，借助于仿真软件，对控制器进行了仿真验证。所搭建的车辆逆纵向动力学模型能较为精准地对期望加速度进行响应，输出节气门开度和制动力。

仿真结果表明：车辆在巡航状态下能控制车速较为精准地保持在理性巡航速度（超调量均小于3%），当设定的巡航车速发生变化时，控制车辆车速能够较快响应；在综合工况中，速度控制和跟车控制正常，且在跟车过程中，车间距误差较小，能够保证较好的跟踪精度。综上，所提出的基于MPC算法的分层控制策略能够实现车辆的自适应巡航功能且保证车辆的行车安全。根据仿真结果可以看出，自适应巡航车辆在低速跟车时，会发生加速度超出期望值的现象，对行车舒适性产生影响。