在高斯分布下优化仿射变换的极限学习机

张 毅，王士同

1.江南大学人工智能与计算机学院，江苏无锡 214122

2.江南大学江苏省媒体设计与软件技术重点实验室，江苏无锡 214122

极限学习机（extreme learning machine，ELM）[1]在各个领域都有着高度的关注和广泛的应用[2-6]。但在取得显著成就的同时，也发现了一些问题，隐含层输出的分布方式关注不够。对比BP（back propagation）神经网络，如果每一层数据的分布方式大相径庭，那么训练就会变得缓慢和复杂，泛化性能大打折扣。反之，如果隐含层输入与输出满足同样的分布方式，不但能够节省训练优化参数的时间，而且能够提高算法的泛化性能[7]。

ELM 利用激活函数将非线性结构带入网络结构，在使用隐节点随机参数带来快速的学习速度和便于实现等特点带来便利的同时，也造成在网络结构中使用固定的激活函数的不足。众所周知，激活函数的选择取决于隐含层输入输出数据的分布[8]。在ELM 中，隐含层的权重和偏置参数具有随机性，且与输入数据无关，使用固定的激活函数计算得到的输出数据，可能会导致不一致的分布方式难以达到良好的泛化性能。由此大量的实验结果表明隐含层输入数据的范围在ELM 中起到关键作用[9]。以ELM最常用的激活函数Sigmoid 函数为例，Sigmoid 函数隐含层输入映射到输出范围，如果输入过大或过小，将落在函数图像的饱和区域，也就是在函数图像中，数据分布过于平缓，由此可知ELM 只会在良好的缩放范围内产生良好的泛化性能。例如gisette（来自于UCI数据集网站）数据集通过Sigmoid 函数映射之后，其结果过度存在集中在0 和1 附近，即Sigmoid 函数的饱和状态，如图1（a）所示。

为了弥补这一缺陷，前人做了大量工作，给出许多方法。DNNs（deep neural networks）采用不饱和的非线性激活函数，如整流器线性单元ReLU（rectifier linear unit）[10]及其改进，包括有参数化ReLU[11]和随机化ReLU[12]等，这种方法能够加快训练速度和泛化能力，但隐节点参数的优化依赖于反向传播算法，收敛速度慢，并且没有足够地研究隐含层数据分布的特性。Zhang 等人[13]利用正则化方法，这种方法只是狭义的参数正则化，在损失函数的基础上加入正则化项来提高泛化性能的ELM 算法（regularized ELM，RELM），能够带来良好的泛化性能。同样，Huang 等人[14]提出基于核方法的KELM（kernel ELM）算法，通过核函数隐式地将输入空间中低维线性不可分样本映射到高维空间中去，能够避免传统的ELM 算法隐含层神经元随机赋值，提高了模型的泛化性和稳定性。Liu 等人[15]提出一种基于多核ELM 的多源异构数据集成框架MK-ELM（multiple kernel ELM），在训练过程中对多个核函数的组合权重和ELM 算法中的结构参数进行联合优化，但对于不同的数据样本，如何自适应地选择核函数和不同核函数的权重系数是个问题。Cao 等人[16]介绍了一种具有仿射变换（affine transformation，AT）输入的新型激活函数，叫作ATELM，文中对比了其中一个算法AT-ELM1。该算法在隐含层输入上加上缩放和平移变换参数。在不需要调整输入权重和偏置的基础上，基于最大熵原理来优化仿射变换参数。此算法一如既往地保持ELM的快速学习速度和良好的泛化性能[17]，并且在激活函数分布范围内，强制将数据大致近似地按照均匀分布输出，来实现隐含层输出数据的最大熵。实际上不尽如人意，隐含层的输入数据无法真正满足最大熵原理，只能通过调节仿射参数让隐含层输出近似达到均匀分布。而且，仿射参数主要是利用梯度下降算法迭代优化的，梯度下降算法中不适当的步长，又难以很好地调节仿射参数。是否还有其他方法让输入数据有更好的效果或者仿射参数是否可能在其他分布方式中表现得更加出色，本文做了一些尝试并取得了一些效果。

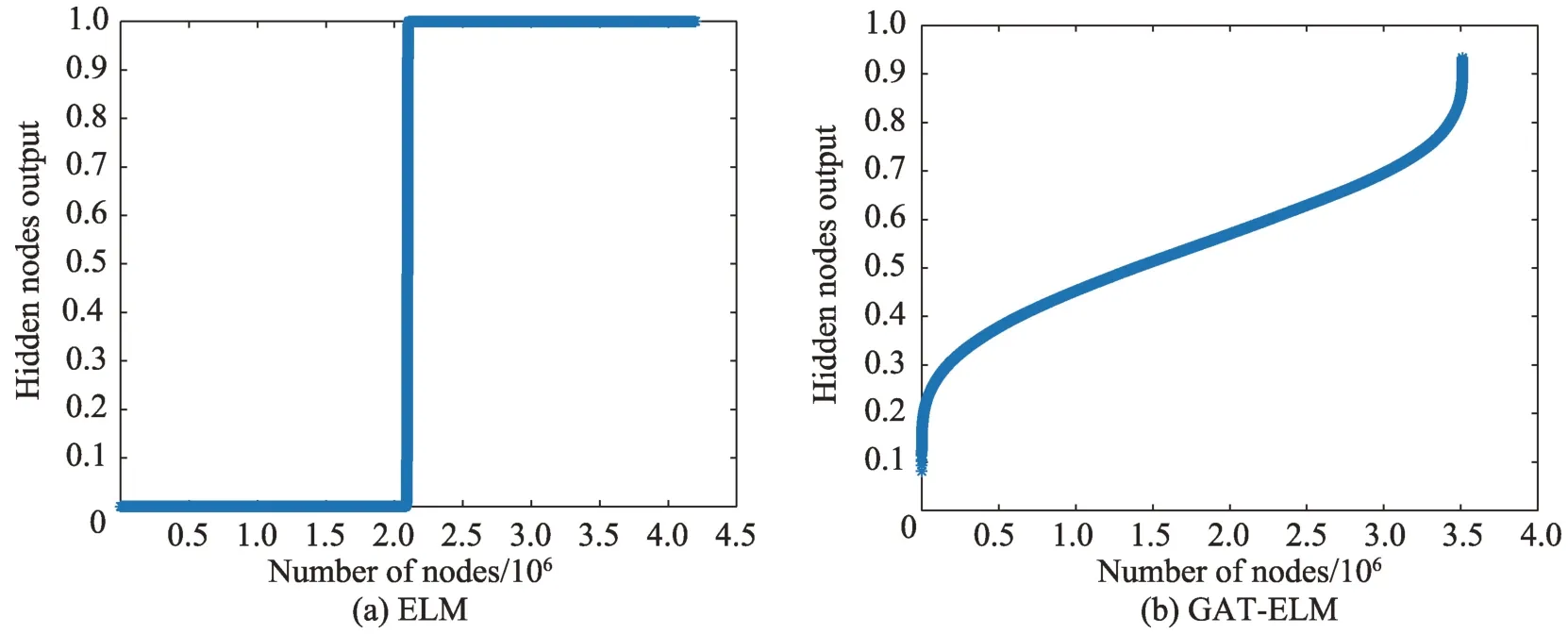
Fig.1 Hidden layer output map of gisette dataset in two algorithms图1 gisette数据集在两种算法中隐含层输出图

为了解决上述问题，本文介绍了一种基于高斯分布来优化激活函数中输入数据的缩放和转换参数，在不需要调整隐含层输入权重和偏置的基础上，调整仿射参数来适应隐含层输入的分布方式，让隐藏层输出的分布在映射后近似于高斯分布。文中采用基于梯度下降的迭代算法来优化仿射参数。

本文的主要贡献概述如下：

（1）利用基于高斯分布计算的仿射参数的方法能够避免激活函数映射之后产生饱和状态，通过调节梯度下降参数迭代优化仿射参数，能够使激活函数主要映射在[0.2，0.8]之间。如图1（b）所示，例中采用gisette 数据集通过Sigmoid 函数映射得到的结果图。数据明显映射在[0.1，0.9]之间，并且绝大部分都在[0.2，0.8]区间内，饱和部分占极小比例。这种优化方式达到的效果明显优于图1（a）。

（2）开发出新型的计算仿射参数的方法，让隐含层输入与输出数据服从高斯分布，那么在这种状态下通过优化参数使整个隐含层输出数据能够满足高斯分布。

1 ELM 简介

本章简要回顾ELM，并给出原始ELM和RELM的求解隐含层输出权重的方法。

原始ELM 作为一种求解单隐含层神经网络的训练框架[18]，其高效的学习速度和易于实现等能力受到极大的关注，成为当前人工智能领域最热门的研究方向之一。在保证算法测试精度的前提下，较于传统的BP 算法[19]，ELM 算法速度更快并且具有良好的泛化性能。ELM 特点在于随机初始化隐含层输入权重和偏置并得到相应的隐含层输出权重。其数学模型表示为：

式中，xi=[xj1,xj2,…,xjn]T表示第i个样本，βi=[βi1,βi2,…,βiL]T是连接第j个隐含层节点到输出层的权重向量。G(wi,bi,xj)表示激活函数，表示隐节点的输入权重和偏置。yj=[yj1,yj2,…,yjm]T是第j个输入样本的网络输出。ELM 理论指出隐节点的参数按照概率分布选取是随机固定的，无需调整[20]。这使得网络模型变成求解线性方程组。

ELM 最初只能用来处理单隐含层神经网络，后来被推广到RBF（radial basis function）神经网络、反馈神经网络、多隐含层神经网络等。整个ELM 模型通过利用如下矩阵乘法得到[21]：

式中，β和T分别为输出层权重矩阵和整个网络的目标输出矩阵，H为隐含层输出矩阵，表示为：

那么输出权重就变成求解线性方程Hβ=Τ的最小二乘解：

其中，H†是矩阵H的广义逆矩阵。

隐节点数是随机的，由通用逼近性可知激活函数无限可微分，隐含层输出近似看成连续函数。

（1）对于隐节点数L等于输入样本个数N，可找到矩阵H，使得=0。

（2）对于隐节点数L不等于样本个数N，对于任意ε＞0，总存在H，使得＜ε。

利用最小方差寻找最优输出权重β，即优化训练误差函数：

标准的ELM 算法是一个基于经验风险最小化原理的训练过程，在没有进行调整隐含层输入随机参数的基础上可能导致隐含层输出数据分布不一致，容易产生过拟合现象，并且当训练样本中出现许多异常点时，隐含层输出具有不适定性。标准正则ELM[22-23]提出用正则化参数λ来平衡误差矩阵和输出权重，正则化理论在本质上是结构风险最小化策略的实现，输出权重β的范数越小，整个网络结构的泛化性能越好。RELM 的数学模型表示如下：

根据隐节点数与样本数的比较，求解式（7）可得RELM的输出权重矩阵β闭式解[24]，其中I是单位矩阵：

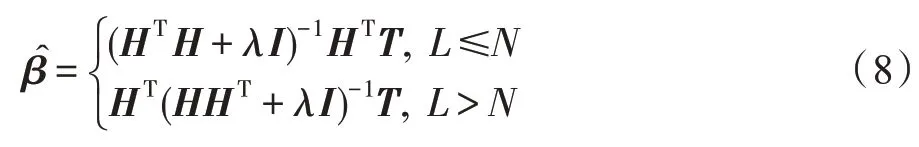
当L≤N时，即隐含层神经元个数小于样本数，此时I为L×L的单位矩阵，而隐含层神经元个数大于样本数时L＞N，此时I为N×N的单位矩阵。显然这样求得的伪逆矩阵简化不少。

2 模型建立

文中提出的GAT-ELM（Gaussian affine transformation extreme learning machine）算法，在保证了ELM的学习速度和泛化性能的同时，也避免了隐含层的输入权重和偏置的迭代，让隐含层输出数据大致映射在激活函数输出的合理范围之内，并且使隐含层输入与输出数据满足高斯分布方式，达到最优效果。

2.1 结构和数学描述

对比其他先进的ELM 网络框架，AT-ELM1算法主要工作是在隐含层，在隐含层中设置的仿射参数由带有均匀分布随机数的目标函数优化，最终目的是能够让隐含层输入与输出服从均匀分布。这种方法的好处是能够让隐含层输入线性映射到更低维空间，以防止最终非线性映射到激活函数特征空间的饱和状态中去。

然而，利用极大熵原理计算仿射参数的做法，也带来一些问题，不足主要体现在以下几点：

（1）完全抛弃了节点之间的依赖性关系[25]。ATELM1算法中让隐含层输出服从均匀分布只是保证了输出数据的独立性，完全抛弃了节点的依赖性关系。因为无论仿射参数如何变化均为线性映射，隐节点始终会保留着依赖关系。要完全忽视隐节点的依赖性，这是远远达不到的，这就是造成不能完全满足均匀分布的主要原因。

（2）隐含层输入数据方差。对于数据本质而言，假设隐含层输入和输出是独立且同分布的，其输入权重和偏置的元素一般在[-1，1]均匀分布或者（0，1）正态分布中产生，且相互独立。则隐含层输入的方差表示为var(vi)=L∙var(wi)+var(bi)[10]。无论权重和偏置在哪个分布下产生，它们均有共同的特点，那就是输入方差与输入数据的数学期望和隐节点的个数有关，并且输入数据的数学期望在一般情况下并不为0，那么隐含层输出便不太可能在激活函数范围内服从均匀分布，引入缩放和平移参数强制映射，效果也可能会差强人意。

（3）激活函数的非线性映射。例如Sigmoid 函数，隐含层输出数据一般为离散的点，根据通用逼近性可知，能够近似形成一条曲线，引入仿射参数之后，为了让输出数据能够很好地服从均匀分布这一方法，需要多次手动的调参来寻找最优的仿射参数，即耗时，同样由于迭代次数和步长选择的限制也无法真正达到最优。

针对上述AT-ELM1算法中求解仿射参数的不足，本文提出一种新的思想，依据如下：

样本数据预处理后，对于单个样本而言，如图2所示，输入层到隐含层为线性映射，从n维的输入层映射到隐含层第一个神经元时，可以看作是线性降维，数据在高维空间中有以下几个特点[26-28]：

（1）数据在高维空间有着低维结构，投影到低维空间不会损失过多判别信息。

（2）高斯分布的数据有着向尾部聚集的趋势，均匀分布的数据有着向角落聚集的趋势，因此在高维空间估计数据的概率分布变得十分困难。

（3）高维数据的低维投影有着符合高斯分布或者高斯分布组合的趋势。维数越大越逼近高斯分布。

（4）在有限个样本的情况下，高维空间的线性可分概率随着维数增加而增加，样本数小于或接近维数时，样本线性可分概率趋于1。

因此，数据由高维向低维映射趋于高斯分布，且维数越大高斯分布趋势越明显。这一显著特征，可以认为在这种映射之后的数据具有高斯分布的特征，且不会带来太大误差。于是，图2 中第一个神经元V1由于输入层神经元个数是远大于1 的，映射之后便有着高斯分布的趋势。对于其他每个神经元而言，同样由输入层映射到当前隐含层神经元，且均为高维向低维映射，按照上述，则同样有着高斯分布趋势。那么这L个独立的隐含层神经元所连接形成的L维隐含层空间Φ(x1)由于空间中的每个神经元均趋于高斯分布，则整体有着高斯分布或者高斯分布组合的趋势。针对整体样本而言，线性映射之后得到的隐含层空间可以表示为：

Fig.2 ELM network structure图2 ELM 网络结构

式中，ℝ 表示为整个隐含层空间，对于每个样本空间Φ(xi)都有着服从高斯分布的趋势，可以假定看作是一组具有高斯分布的离散数据，那么这N个样本所连接形成的整个隐含层空间就可以被认为是N组具有高斯分布的离散数据的集合。在这种条件下，整个隐含层空间就符合高斯分布或者高斯分布组合的趋势，且维度越大，低维映射呈高斯分布趋势越明显。同样对比本文使用的数据集，也能够发现在绝大多数的数据集中，隐含层输入有着明显的高斯分布趋势。对大样本数据而言，隐含层输入矩阵如果隐节点数小于或者接近输入样本数，同样遵循高斯分布趋势。

如果利用极大熵原理让其强制均匀分布，这种做法虽然在理论上说得通，但是在实际应用中却只能近似达到，因为样本特征之间有着一定的关联性，均匀分布忽略了这种依赖关系，只保证了节点之间的相互独立。而节点之间的依赖性是网络结构中不可忽视的关键因素，因为在映射过程中，需要尽量保留输入数据特征，减少特征丢失。而采用极大熵原理的AT-ELM1算法让隐含层输入与输出满足均匀分布具有一定局限性，本身激活函数映射就是非线性映射，如果映射结果是线性的，必然不可避免地丢失了很多数据特征，这样模型就变得不可靠。如何让数据特征能够尽量保留是必要的。而高斯分布是一种非线性结构，从这点来看，比均匀分布增强了一定的模型可靠性。由此来看，隐节点的依赖性在模型结构中是必不可少的。

具体说明，引入四组向量X1,X2,X3,X4，其中w13,w23,w14,w24是节点之间的连接权重，有着高斯分布的趋势，每个向量有m个特征。其依赖关系可以理解为：对于X1节点，其输出对于节点X3、X4的计算是必需的，同样节点X3、X4彼此不需要来自对方的任何信息，则称两者是相互独立的，对此进行可视化，如图3 所示。

Fig.3 Dependency diagram图3 依赖性关系图

对比整个输入层映射到隐含层输入的过程，隐节点均包含着来自输入层的直接依赖关系，这是不能忽略的重要因素，如果让隐含层输入不考虑依赖关系，让其服从均匀分布，是做不到的，始终存在着这层直接或者间接的依赖关系。文中提出改进算法让隐含层输入服从高斯分布，通过不断修正隐含层输入与输出的分布方式，在原始隐含层输入与输出的基础上，引入仿射参数，不断调节达到最优效果，具体设置思路下文阐述。这种做法能够有效保留隐节点的依赖性，又能够做到相互独立。这极大地表明了隐含层输入服从高斯分布具有可靠的理论基础，利用这方面作为切入点，假设隐含层输入能够服从高斯分布，按照隐含层输入与输出同分布的原则，让隐含层输出也服从高斯分布。

为了更好地让隐含层输入与输出服从高斯分布，文中介绍一种新的仿射参数计算方法，称之为GATELM 算法，主要思想：在隐含层输入原本有着高斯分布趋势的情况下，由于其本身可能只是近似服从高斯分布，且不可能完全服从，只能让隐含层输入强制服从高斯分布，且一般的激活函数映射模式会让隐含层输出趋于饱和状态。于是，对隐含层输入添加缩放和平移参数，如果隐含层输入数据过大，那么可以使用较小的仿射参数，对数据二次加工让数据值缩小，同样，如果隐含层输入数据过小，则需要较大的仿射参数。这都能使隐含层输入通过激活函数之后不会大量映射到饱和状态。那么如何确定仿射参数就是一个寻优的过程，文中采用梯度下降算法优化缩放和平移参数，能够使隐含层输出服从高斯分布。这种缩放、平移参数的设置能够很好地调节隐含层输出的范围，极大地提高了模型的泛化性能。

2.2 在高斯分布下的仿射变换的参数优化

在原始ELM 算法中，数据集均生成在一定范围内，给出预处理之后的训练集，随机生成隐含层输入权重和偏置，让G(wi,bi,xj)作为整个数据集的激活函数，且固定不变，计算得出训练样本的隐含层网络输入矩阵V：

本文在参数优化过程中，为每个仿射参数得出相对应的误差函数，进行迭代优化。其目标优化函数为：

式中，m和n为仿射变换参数，其为隐含层激活函数输出范围内随机生成的两个高斯分布随机数，列向量v是由矩阵V中的每一个元素按从小到大排列而成，v=[v1,v2,…,vk,…,vN×L]T(v1＜v2＜…＜vN×L)，I=[1,1,…,1]T∈RN×L是元素全为1 的列向量，向量u表示为v的同型向量，且其中的每一个元素都是服从高斯分布的随机数，并在隐含层激活函数输出范围内按从小到大排列u=[u1,u2,…,uk,…,uN×L]T(u1＜u2＜…＜uN×L)。

式（12）和式（13）可以进一步化简为：

可以发现在计算对m和n的偏导时，对于每一组仿射参数均可提前计算找公共部分，这样可以降低计算的复杂度，提高模型效率。然后，利用梯度下降算法分别为仿射参数进行优化，得到全局最优解。本文所述方法能够让隐含层输入输出数据映射到高斯分布的空间中去。

本文中GAT-ELM 算法思想是在AT-ELM1算法上改进，对比基于极大熵原理的AT-ELM1算法，GATELM 算法无论在公式上，还是结果上都与之不同。主要不同之处在于求解仿射参数的方法，让高斯随机数组成的向量u放入目标函数中。实验对比，通过算法1 优化，能够得到更佳的效果。

具体的仿射参数的计算方法如下所示。

算法1高斯分布下的仿射变换的参数优化方法

输入：设定激活函数为Sigmoid 函数，梯度下降算法的输入步长η（按照实际情况），最小度量ε，最大迭代次数K，设置下采样Nd。

输出：仿射参数m和n。

1.计算出合适的仿射参数

1.2 隐含层输入权重W和偏置b随机产生，计算出隐含层输入矩阵V，并将V中的每一个元素按从小到大排列。

1.3 在激活函数的特征空间ℝ 内生成高斯分布随机数，并从小到大排列成u=[u1,u2,…,uk,…,uN×L]T。

1.4 根据下采样Nd，得到采样后的。

1.5 随机初始化仿射参数m、n，计算出式（14）的初始值，并计算φ。

1.6 按照梯度下降算法迭代计算m、n，更新式（14），得到每次迭代后的φ值。

1.7 输出优化后的仿射参数m、n的值。

end

由于假定对隐含层网络输入数据的分布方式没有任何限制，即此算法适用于训练数据的任何分布方式和任何随机生成的隐含层输入权重和偏置。在算法1 中，考虑到训练样本和隐节点的个数严重影响着计算仿射变换参数m、n的时间复杂度，本文中引入下采样计算方法，在较小影响精度的前提下，极大地降低算法的时间复杂度。

2.3 优化正则化参数和隐含层输出权重算法

求解正则化参数的方法来源于RELM 算法中的LOO（leave one out）交叉验证策略[29]，主要原理是指整体样本分割成N个子样本，其中N-1 个样本为训练集，剩余的一个为测试集，多次实验，对λ进行寻优，一般地，正则化参数在区间[λmin,λmax]选择[29]。

在优化λ的过程中为了减少LOO 中性能评估指标MSEpress公式的计算复杂度，降低HAT 公式中的矩阵H重复计算，引入SVD 算法，令H=UDVT，U,V均为酉矩阵，即UTU=I,VTV=I。由此解出隐含层输出权重β[29]：

式中，当L≤N时，HTH=VD2VT，利用SVD 算法，VTHTT和HV均可提前求出；当L＞N时，HHT=UD2UT，同样，HTU和UTT也可提前解出。

本文中的ELM 算法可以大致描述为：首先利用算法1 来优化仿射参数m、n，然后通过RELM 中的LOO 交叉验证方法和MSEpress计算优化λ算法。最后通过在高斯分布下优化的仿射参数m、n和正则化参数λ计算隐含层输出权重，如下描述优化ATELM1中的λ参数和隐含层输出权重β。

算法2优化隐含层输出权重算法

输出：隐含层输出权重和正则化参数。

1.计算出隐含层输出权重

1.3 利用算法1 中优化计算后的仿射参数mopt、nopt，计算隐含层输出矩阵。

1.4 当L≤N时，计算E=HV,F=ETT和d=(diag(D2))T；当L＞N时，计算E=HHTV,F=UTT和d=(diag(D2))T。

1.5G=E⊙repmat(1./(d+λ),N,1),R=norm((T-GF)./repmat(1-sum(G⊙E,2),1,m))，MSEpress=R2/N，当MSEpress取最小时，输出此时的λopt。

1.6 通过公式求出βopt：当L≤N时βopt=V⊙repmat(1./(d+λopt),L,1)F;反之βopt=HT(U⊙repmat(1./(d+λopt),N,1))F。

end

为了表现算法的改进效果，与原始ELM、ATELM1进行了比较。同时，为了能够更加实际地与AT-ELM1算法比较，文中所涉及的数据集与AT-ELM1文献中的保持一致。

3 实验结果和分析

3.1 实验设置

为了体现GAT-ELM 算法在实验稳定性方面的优势，本文选取了传统的ELM 算法和文献[16]提出的AT-ELM1算法进行比较。

隐含层节点数目L的寻优范围根据样本大小分别标明，梯度下降算法的实际步长、最小度量、最大迭代次数、下采样数设置如表1 所示。

实验过程中，按照不同的比例把实验数据作为训练样本和测试样本，为了有效评估算法的性能，采用正确率和标准差作为性能指标。此外，参数规模设置分析如下：

（1）由式（1）可知，样本个数设置为N，隐含层节点数设置为L，输出层节点数为m个。这部分主要分为三步，首先输入层到隐含层，其次隐含层激活函数映射，最后隐含层到输出层，那么总的参数规模为N×L+N×L+N×m。

Table 1 Gradient descent algorithm parameter settings表1 梯度下降算法参数设置

（2）由算法1 可知，梯度下降算法中迭代次数为K，下采样数为Nd，则算法1 参数规模为K×Nd。

（3）由算法2 可知，假设正则化参数λ有M个，此参数规模为M+m×L。

则累加为N×L+N×L+N×m+K×Nd+M+m×L。

实验平台为Intel Core i5-3470 处理器；主频为3.60 GHz；内存为8 GB；系统类型为Win7 32 位操作系统；编程环境为Matlab R2018a。

3.2 以实际手写数据集为例演示重要步骤及反映真实结果

为了测试仿射变换参数的效率，本文测试了MNIST（有关数据库的详细描述，请参见第3.3 节）数据集。MNIST 包含了手写数据的二进制图像，原始数据集包含了60 000 个训练样本和10 000 个测试样本。文中采用了两种设置方法，假设训练样本和测试样本共享相同的分布。对于每个图像而言，灰度像素均为特征。测试1，在训练样本中随机选取2 000 个用于训练，测试样本也选取2 000 个，其隐节点范围为[400：200：2 000]。测试2，在训练样本中随机选取10 000 个用于训练，测试样本则选取全部，隐节点取值范围为[2 000：200：4 000]。在两者实验中，LOO 交叉验证算法的搜索范围均为利用固定的隐节点激活功能，ELM 对输入变量的范围缩放非常敏感。分析这两个实例可以得出，ELM 的输入数据放缩在[-10，10]之间，其表现良好，然后再通过不同的缩放因子γ调整数据的大小，以研究该算法的实际泛化性能，也就是说，文中所有用到的数据集，在预处理阶段，原始样本都在[-10，10]中生成，然后按如下因子缩放：

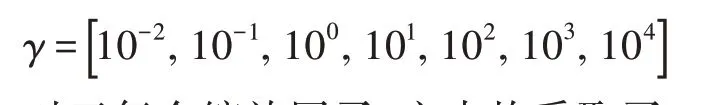
对于每个缩放因子，文中均采取了10 次实验，计算平均结果。分别计算出三种算法（ELM、AT-ELM1、GAT-ELM）每个缩放因子的均方误差并做出比较。如图4（a）中，当使用固定的Sigmoid 时，GAT-ELM 算法的性能比ELM 和AT-ELM1都有一定幅度改进。对比ELM 算法而言，RMSE 降低了39.28%，同样对于AT-ELM1也降低了10.52%。总体而言GAT-ELM 相比于前两个有着明显的提升。对图4（b）具体说，当γ大于100 时，ELM 算法中RMSE 值越来越大。相反，由于激活函数可以调整仿射参数让隐含层输出服从高斯分布，因此本文中的GAT-ELM对于所测试的缩放因子均具有良好的一致性。以具体结果为例：当γ=0.1 时，所得到仿射参数(aopt,bopt)=(-1.404 0，0.049 5)。在γ=100的情况下，为了弥补样本输入中缩放因子的变大，得到仿射参数(aopt,bopt)=(-0.151 5，0.145 1)。

Fig.4 Comparison of experimental results图4 实验结果比较

为了更好地比较文中GAT-ELM 算法与AT-ELM1算法，测试结果如表2 所示。

Table 2 Results of test 1 and test 2表2 测试1 和测试2 的结果

对比三种算法，得到如下结论：

在测试1 中GAT-ELM 算法相较于ELM，精度提高了8.05%，标准差降低了34.32%；同样对于ATELM1，精度提高了1.60%，标准差降低了15.4%。

在测试2 中GAT-ELM 算法相较于ELM，精度提高了1.50%，标准差降低了50.00%；同样对于ATELM1，精度提高了1.29%，标准差降低了20.00%。

根据实验结果可以知道，在测试1 和测试2 中，在高斯分布下计算的仿射参数，提高了算法的稳定性，并且泛化性能也有一定的提升。除了泛化性能外，训练时间是ELM 算法中的另一个问题。文中的算法时间主要是通过LOO 交叉验证算法寻找最优λ的代价时间，那么λ∈[λmin,λmax]的范围越大，训练时间就越长。由于AT-ELM1和文中GAT-ELM 的正则化参数λ的范围是一致的，并且梯度下降算法中各个参数设置一致，整个模型的参数规模可以是接近的，参数规模且都高于原始ELM，即两个算法的训练时间总体是一致的，都明显高于原始ELM。

3.3 真实数据集中的分类

为了更好评估算法的性能，测试了12 种涵盖了许多实际应用的基准分类数据集，前9 个来自UCI 数据集网站（http://archive.ics.uci.edu/ml/index.php），后面3 个来自特征选择网站（http://featureselection.asu.edu/datasets.php）。如表3 所示，表中涵盖了所测试的基准分类数据集的样本特征维数、训练样本数、测试样本数和类别数。

对于所有数据集，所有样本均用于分类算法的训练和测试，为了更加直观对比AT-ELM1算法，本文实验中的训练样本和测试样本都与AT-ELM1算法中的分配所相同，与此同时，其隐含层寻优区间也相似。对于较小的数据集，例如Breast、Diabetic 和wine在[100：50：600]之间寻找最佳的隐节点数。像大样本数据集OnlineNews 在[500：100：2 500]范围内搜索隐节点的最佳数目。剩余数据集在[500：100：1 500]寻找最佳的隐节点数目。算法2 利用LOO 交叉验证方法在{e[-10:0.2:10]}寻找最优正则化参数λ。原始ELM、AT-ELM1和本文中GAT-ELM 的精度和标准差结果都在如下表格中进行比较。其中Percentage1=(GAT-ELMELM)/ELM 和Percentage2=(GAT-ELM-AT-ELM1)/AT-ELM1分别表示GAT-ELM 算法对比原始ELM 算法和AT-ELM1算法的精度和标准差的变化率，Ai-Rate 表示新的算法精度相较于对比算法提高的百分比，R-Std 表示新的算法方差相较于第一个算法降低的百分比。

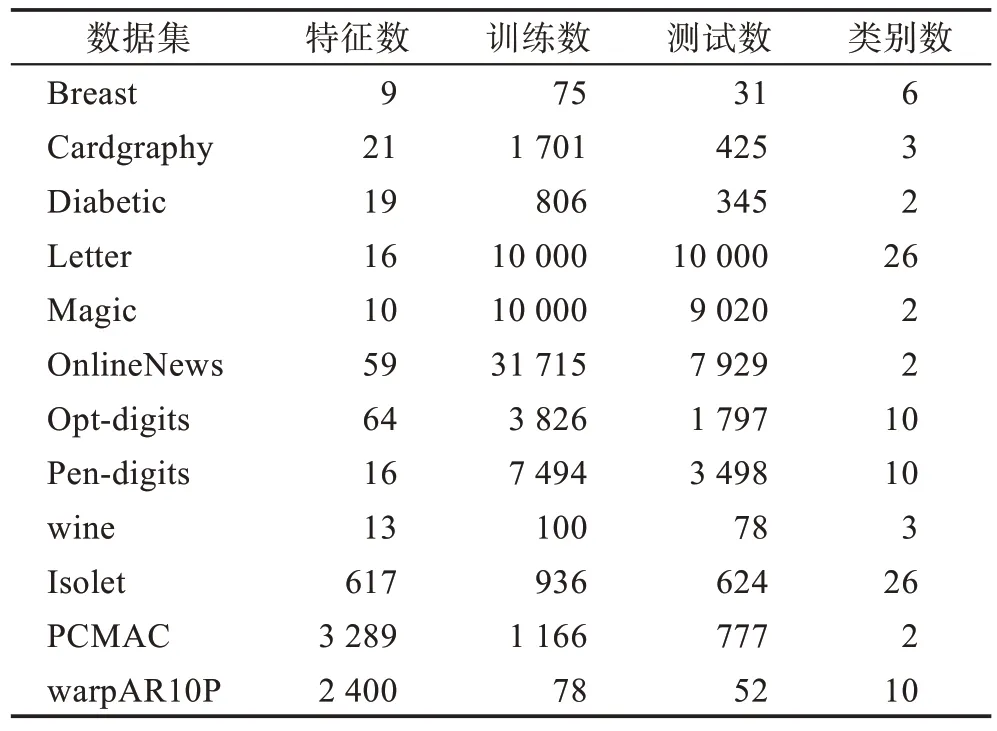
Table 3 Details of 12 datasets for UCI and feature selection表3 UCI和特征选择的12 个数据集的详细信息

针对ELM、AT-ELM1、GAT-ELM 三种算法，表4对最优精度采用加粗，对最优标准差加下划线。在这12个分类数据集中，由于引入了仿射参数，AT-ELM1算法和GAT-ELM 算法的分类精度和标准差均优于原始ELM 模型。对于多数分类数据集而言，GATELM 算法的标准差明显低于AT-ELM1，在所测数据集中，可以发现Breast、Diabetic、Letter、Opt-digits、Pen-digits、wine、Isolet、PCMAC、warpAR10P 数据集在GAT-ELM 算法中的测试精度更加集中，并且两种算法精度之间的落差范围很微小。

同样，Breast、Cardgraphy、Magic、OnlineNews、Opt-digits、Pen-digits、wine、Isolet、PCMAC 数据集在测试精度上GAT-ELM 比AT-ELM1高。Breast、Optdigits、Pen-digits、Isolet、PCMAC 数据集在精度和标准差上GAT-ELM 均优于AT-ELM1。并且，GAT-ELM算法比较原始ELM 算法，在精度提升方面最高达到112.44%，并且在标准差上也有明显的改善。同时对比AT-ELM1算法，在精度方面变化率保持在（-1.5%，2.5%）之间，但标准差方面最高有着53.85%的下降。

Table 4 Test results and performance comparison of benchmark datasets using Sigmoid function表4 使用Sigmoid 函数对基准数据集的测试结果与性能比较

与此同时，本文中对比分析隐含层输出情况，原始ELM 的性能较差主要是由于这些数据库的隐藏节点输出大部分位于Sigmoid 的饱和区域或平坦区域中。为了直观表现，本文用案例进行了可视化分析，图5 比较了warpAR10P 和Pen-digits 数据集在原始ELM、AT-ELM1和GAT-ELM 的隐节点输出。在ELM算法中，使用固定的Sigmoid 函数，warpAR10P 和Pen-digits 的隐节点输出主要在激活函数特征空间的平坦区域。在AT-ELM1算法中，隐含层输出无法真正达到均匀分布。相反，本文中介绍的让隐含层服从高斯分布的GAT-ELM 算法能够让隐含层输出更加契合高斯分布。

由于采用不同的隐节点数，缩放参数和下采样率可能会影响分类精度，针对warpAR10P 和Pendigits 数据集的结果，文中测试隐节点数均为1 500，缩放参数均为0.1，下采样率分别为500 和5 000，对正则化参数利用LOO 交叉验证方法寻优的结果分别是0.110 8 和1.822 1，所求精度也均高于平均精度。

3.4 图像回归

本节介绍了4 种图像数据库，详细描述如下：

Fig.5 ELM，AT-ELM1，GAT-ELM hidden node output of warpAR10P and Pen-digits datasets图5 warpAR10P 和Pen-digits数据集的ELM、AT-ELM1、GAT-ELM 的隐节点输出

Table 5 Test results and performance comparison of image datasets using Sigmoid function表5 使用Sigmoid 函数对图像数据集的测试结果与性能比较

USPS 数据库：包括0～9 的10 个数字，总计9 298个手写样本。每个样本的16×16 灰度图像直接用数字表示，7 500个样本用于训练，其余用于测试。

Yale 数据库：165 张表情图像，包括15 个类别数。每个样本由32×32 灰度图像构成，实验中，60%的训练样本随机生成，其余用于测试。

Yale(B)数据库：包括38 个不同的个体共2 204 个样本。每个样本有32 256 个特征，实验中，随机产生50%的训练样本，另一半用于测试。

ORL 人脸数据库：有40 个不同对象的相同图片，每个对象收集了10 个不同细节，采用32×32 的灰度图像的像素作为特征。随机产生60%的样本用于训练，其余用于测试。

与分类数据集一致，图像数据集也需要在一定的范围搜索最佳隐节点数目，对于ORL 数据集为[100：100：1 000]，而对于Yale 数据集、Yale(B)数据集则在[400：200：2 000]中寻找，[1 000：200：3 000]适用于USPS 数据集。针对ELM、AT-ELM1、GAT-ELM 三种算法，表5 对最优精度采用加粗，对最优标准差加下划线。在这4 个图像数据集中，由于引入了仿射参数，AT-ELM1算法和GAT-ELM 算法的分类精度和标准差均优于原始ELM 模型。与此同时，在4 个测试实验中，GAT-ELM 的标准差明显低于AT-ELM1，精度都有小幅度提升。为了进一步直观表明GAT-ELM的性能，表5 计算出了性能表现率，从表中可以清楚看出，GAT-ELM 算法与原始ELM 算法相比，精度提高率最高达到44.68%，并且标准差下降了93.59%。同样对于AT-ELM1算法而言，精度之差在[0.20%，1.60%]，相比较精度变化范围不大，标准差变化明显，GAT-ELM 算法下降了最高62.96%。

对比4 组测试实验，可以发现在这些数据集中，本文介绍的GAT-ELM 算法在精度方面略优于ATELM1，而算法的稳定性却得到很大的提高。

4 结束语

本文从理论上分析了让隐含层输出近似服从均匀分布却无法真正达到这一问题。探讨了节点依赖关系必要性。针对这一研究，本文提出了一种在高斯分布下计算仿射参数的算法。上述算法首先对原始输入数据寻找合适的放缩参数和最佳隐节点参数，然后通过梯度下降算法优化仿射参数，最后利用均方误差最小值确定最优正则化参数和隐含层输出权重。实验表明：该算法与AT-ELM1有着近似的计算时间，并且在保留隐节点依赖性的基础上，利用梯度下降优化仿射参数让隐节点输入与输出都共同满足高斯分布比利用极大熵原理的AT-ELM1表现得出色。在实验结果上，大多数数据集在高斯分布下取得更好的效果。