基于IDEPSO-SS的多工况转向架构架可靠性分析
智鹏鹏,王悦东,汪忠来,李永华,张 明
(1.电子科技大学 机械与电气工程学院,四川 成都 611731;2.大连交通大学 机车车辆工程学院,辽宁 大连 116028;3.中车唐山机车车辆有限公司技术研究中心,河北 唐山 063035)
转向架构架作为轨道车辆结构设计中的大型复杂部件,通常依靠确定性的有限元分析预判结构在设计阶段是否满足标准要求。然而,无论是静强度分析,还是疲劳强度分析,分析结果均较为理想化,与试验数据偏差较大。其原因在于分析中采用的确定性有限元模型忽略了构架在设计与制造过程中的不确定性因素,例如:材料属性、设计公差、加工偏差和试验载荷等[1]。因此,将可靠性理论与有限元分析相结合,利用可靠度评判构架在设计阶段的静态性能,可以更好地反映设计的合理性。
针对结构可靠性分析方法如何更好地应用于工程实际,部分学者进行了深入研究。卢耀辉等[2]考虑了影响构架最大主应力的随机变量,采用概率设计方法建立参数化模型,采用Monte Carlo 模拟(MCS)方法计算转向架构架的可靠度及灵敏度。滑林等[3]分别从区间变量随机化和随机变量区间化的角度,对船体进行可靠性分析,提高了可靠性分析的准确性和实用性。杨瑞刚等[4]鉴于起重机金属结构不确定性设计变量的随机性、模糊性和非概率性,提出一种多源不确定性混合可靠性分析方法,使可靠度结果更加符合工程实际。黄洪钟等[5]为解决现有方法进行数控机床不确定性问题可靠性分析时的局限性,基于不精确概率理论提出一种混合不确定性量化方法。此外,为解决大型复杂结构存在的物理模型难以获取、可靠度求解难度大等问题,姜潮等[6]在考虑不确定性因素的基础上,采用径向基函数代理模型表征工程机械臂参数与其固有频率之间的函数关系,采用概率-区间混合可靠性分析方法对失效概率进行估计;Zhi 等[7]建立转向架构架的多级响应面代理模型,运用Monte Carlo 模拟计算转向架构架的可靠度。为提高复杂结构可靠性分析的精度,Echard 等[8]提出一种结合Kriging模型和MCS的主动学习可靠性分析方法(AK-MCS);Huang 等[9]采用基于Kriging模型和子集模拟(Subset Simulation,SS)的主动学习小失效概率评估方法(AK-SS),对某盾构隧道的可靠性进行分析。然而,上述研究仅能反映结构在单工况下的可靠性水平,未考虑结构的多工况和多随机响应特性。
Li等[10]提出改进的SS方法,解决了实际工程中结构多随机响应的可靠性问题。该方法虽然能够对多随机响应的失效概率进行快速求解,但是计算结果受每层样本个数和初始条件概率等参数随机性的影响,并且仅适用于随机变量相同的性能函数。Xiao等[11]提出一种基于主动Kriging模型的混合变量结构可靠性分析方法,解决了复杂结构中子结构的失效概率问题,但是未考虑各工况之间的相关性,并且不便于多个独立随机变量结构的工程应用。
本文以某型转向架构架为研究对象,采用改进差分进化粒子群算法(IDEPSO)获取最优的每层样本个数和初始条件概率,以提高SS 方法的求解精度,进而采用几何分析确定联合失效概率,计算多工况下构架的可靠度及最优失效次序,并与传统方法进行对比,验证基于IDEPSO-SS可靠性分析的准确性,为设计阶段转向架构架在多种组合工况下的总体性能分析方法由传统的确定性分析向不确定性分析转变提供理论参考。
1 基于IDEPSO-SS的多工况可靠性分析
1.1 基于SS方法的失效概率求解
SS方法的基本思想是将小失效概率的求解过程,通过马尔可夫链蒙特卡罗(Markov Chain Monte Carlo,MCMC)方法生成条件样本,进而转换为一系列较大条件失效概率乘积的模拟过程,解决了MCS方法在求解工程小失效概率时效率较低的问题。
若自适应引入的中间事件满足嵌套关系,L1L2…Lm=L,则目标失效概率PL为

式中:L为目标失效事件;Li为第i层的中间失效事件;P(L1)为首次失效的概率;P(Li|Li-1)为Li对应的条件概率。
在采用SS 方法求解之前,首先需要设置所有条件概率P(Li|Li-1)的初始值P0,进而确定各中间失效事件。若第i层模拟中使用的样本个数为N,则第i层条件概率的估计值为

式中:为第i层模拟得到的失效概率估计值;ILi+1为示性函数;{xk|k=1,2,…,N}为独立同分布样本集合。
将式(2)带入式(1)得
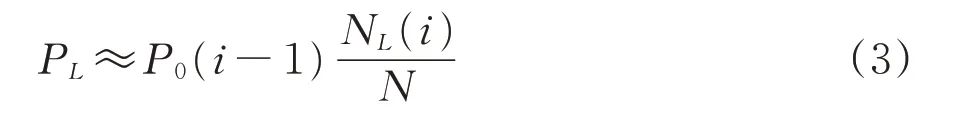
式中:P0(i-1)为第i层的初始条件概率;NL(i)为第i层落入失效域的样本个数。
1.2 基于IDEPSO算法的失效概率优化
通过以上分析可知,每层样本个数和初始条件概率对失效概率估计值的影响较大。传统依据经验确定的每层样本个数和初始条件概率很难得到结构的最优失效概率。基于此,采用IDEPSO算法优化高阶响应面代理模型,获得最优每层样本个数和初始条件概率,从而计算单工况最优失效概率。
假设1个D维的搜索空间中包含了B个粒子,则第i(i=1,2,…,m)个粒子可表示为1个D维向量:Xi=(xi1xi2…xiD),个体最优位置为Z=(Zi1Zi2…ZiD),群体最优位置为G=(Gi1Gi2…GiD)。当2个最优位置确定后,可根据式(4)更新粒子的速度和位置。
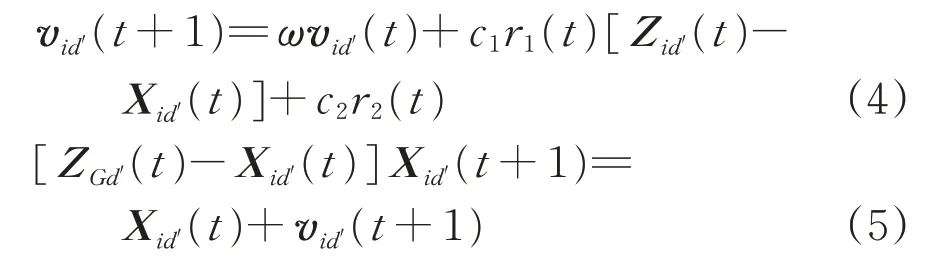
式中:vid′为迭代过程中的粒子速度;t为迭代次数;Zid′为迭代过程中的个体最优位置;Xid′为迭代过程中的粒子位置;ZGd′为迭代过程中的群体最优位置;ω为惯性权重;c1和c2为学习因子;r1和r2为[0,1]内的均匀随机数。
PSO算法虽然能够以较大的概率收敛于全局最优解,并且避免复杂的遗传操作,但是由于最优粒子的速度和位置更新后可能为零,没有自主进化机制,因此极易陷入局部最优解,出现早熟停滞现象。
为解决这一问题,采用改进差分进化算法(IDE)优化PSO算法。研究表明,采用不同的变异策略使得算法的搜索能力不同,文献[12]采用的变异策略具有较强的全局搜索能力,而文献[13-14]采用的变异策略具有较强的局部搜索能力。为增强PSO算法的综合搜索能力,避免不同变异策略出现寻优早熟现象,提出IDE算法的混合变异策略为
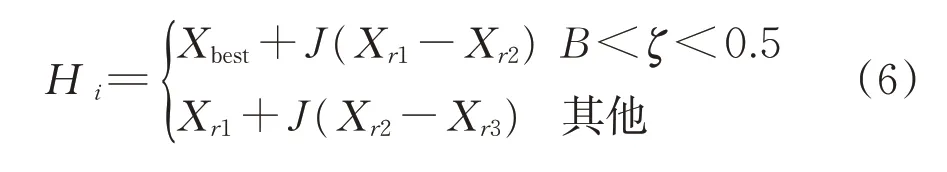
其中,
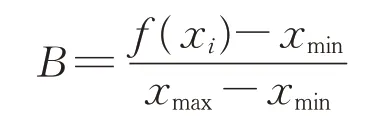
式中:H i为变异操作中任一变异个体集;J为缩放因子,J∈(0,1);Xbest为当前代中最优个体;Xr1,Xr2和Xr3为当前代中随机选取的个体,其中r3为[0,1]内的均匀随机数;ζ为(0,1)之间均匀分布的随机数;f(xi)为第i个粒子的适应度;xmin和xmax为粒子中的最小值和最大值。
1.3 多工况结构失效概率计算
对于转向架构架而言,在设计阶段需要满足的工况较多,仅对单一工况进行可靠性分析得到的设计结果局限性较大。为全面分析结构设计的合理性,基于最优失效概率,采用二阶窄边界法(Ditlevsen法)和最优准则计算多工况下结构的最优失效次序和可靠度。
二阶窄边界法[15]由于考虑了各工况失效的相关性,被广泛应用于多工况下的可靠度计算。多工况失效概率Pf的表达式为

式中:Pij为工况i与工况j同时失效的概率,即联合失效概率。
由式(7)可知,Pij的计算精度直接影响多工况下失效概率的界宽。虽然采用数值积分和MCS方法能够较为精确地计算Pij值,但是不利于工程应用。
为了兼顾联合失效概率的求解精度和效率,采用基于几何分析的联合概率计算方法确定Pij[16]。Pij的表达式为
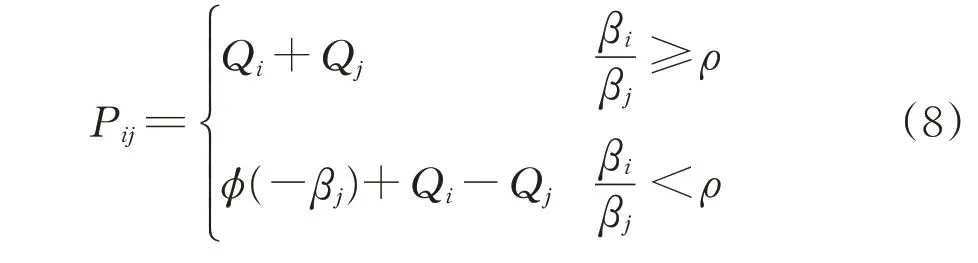
其中,
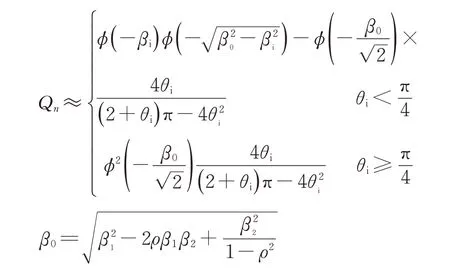
式中:φ为标准正态分布的分布函数;Qn(n=i,j)为几何关系确定的2个工况间的失效概率,其求解表达式相同;βn为工况i和工况j的最优失效概率对应的可靠性指标;ρ为工况失效时的相关系数;β0为中间参数;θn为各工况可靠性指标间的夹角。
将最优失效概率代入式(8)计算得到联合失效概率Pij,并代入式(7)得到多工况下失效概率的界宽估计值。虽然该值在计算精度上有所提高,但是受多工况下结构失效次序的影响较大。
1.4 最优失效次序的确定
由式(7)可知,多工况下失效概率界宽的最大下界即为最优可靠度(可靠度的最小上界)。为保证计算结果不受工况失效次序的影响,若对任意事件i不等式成立,则式(7)的下界可改写为
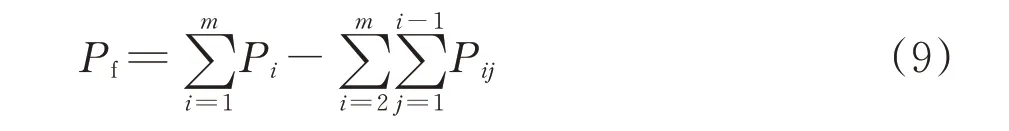
由式(9)可知:相比采用式(7)求解的多工况失效概率,采用式(9)求解时,工况的失效次序对Pij的值没有影响,其最大值即为所需的最大下界。为此,给出采用最优准则法求解式(9)的最大值,具体步骤如下:
(1)结合第1.1 和1.2节计算各工况的最优失效概率,根据1.3节计算各工况的联合失效概率Pij;
(2)选择失效概率中的最大值,并将其排序为λ;在余下的失效概率中选择工况序号ξ,使得pξ-pλξ的值最大,并将其排序为λ′;
(3)在除最大失效概率外的其他失效概率中选择工况序号ξ,使得pξ-pλξ-pλ′ξ最大,并将其排序为λ′′;
(4)重复上述步骤,直至剩余的失效概率满足不等式pξ-pλξ
综上所述,可得基于IDEPSO-SS的多工况下转向架构架可靠性分析流程如图1所示。

图1 多工况下转向架构架可靠性分析流程
2 基于SS的构架失效概率响应面代理模型
2.1 构架静强度响应面函数
考虑不确定性因素对构架静强度的影响,建立不确定性参数关于静强度的响应面函数,是对构架进行可靠性分析的基础和前提。以某型转向架构架为对象进行分析,该构架由横梁、纵梁、牵引座等组成,分别采用壳单元和实体单元建模。考虑一系悬挂对转向架构架的影响,建立COMBIN14 单元模拟弹簧,单元刚度与一系悬挂相同,有限元模型如图2所示。
根据标准UIC 615-4《移动动力装置-转向架和走行装置-动力转向架构架强度试验方法》和EN 13749《铁路应用-轮对和转向架-转向架结构要求的规定方法》分别计算构架主体超常载荷、牵引拉杆纵向冲击载荷、电机振动冲击载荷、电机短路载荷和制动座载荷。依据设计需求对载荷进行组合,限于篇幅,仅选取4种组合工况为例进行分析,具体见表1和表2。
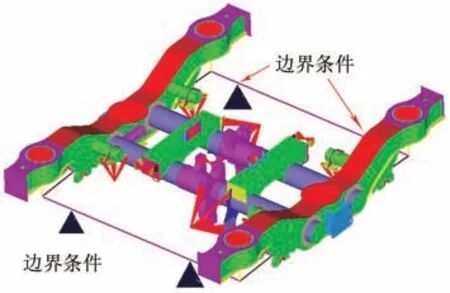
图2 转向架构架的有限元模型

表1 超常工况载荷

表2 特殊超常工况载荷
转向架构架结构静强度采用当量应力表示,在超常载荷工况下,母材当量应力应小于相应材料安全系数S=1.0时的许用应力,焊缝当量应力应小于相应材料安全系数S=1.1时的许用应力[17]。转向架构架组成材料及其力学性能见表3。

表3 构架组成材料的力学性能
根据构架的有限元模型及其组合工况计算静强度,基于分析结果确定对最大应力影响较大的设计参数,其统计特征见表4。表中:d1-d5为对各工况下对静强度影响较大的尺寸参数;F1-F5为对各工况下对静强度影响较大的载荷。

表4 设计参数的统计特征
基于表4提供的不确定性设计参数,建立各工况对应的构架静强度响应面函数,其表达式S1-S4分别为

2.2 静强度响应面函数的精度检验
为检验各工况下构建静强度响应面函数的拟合精度,对式(10)—式(13)进行方差分析(Analysis of Variance,ANOVA),其中工况1和工况4的部分分析结果分别见表5和表6。
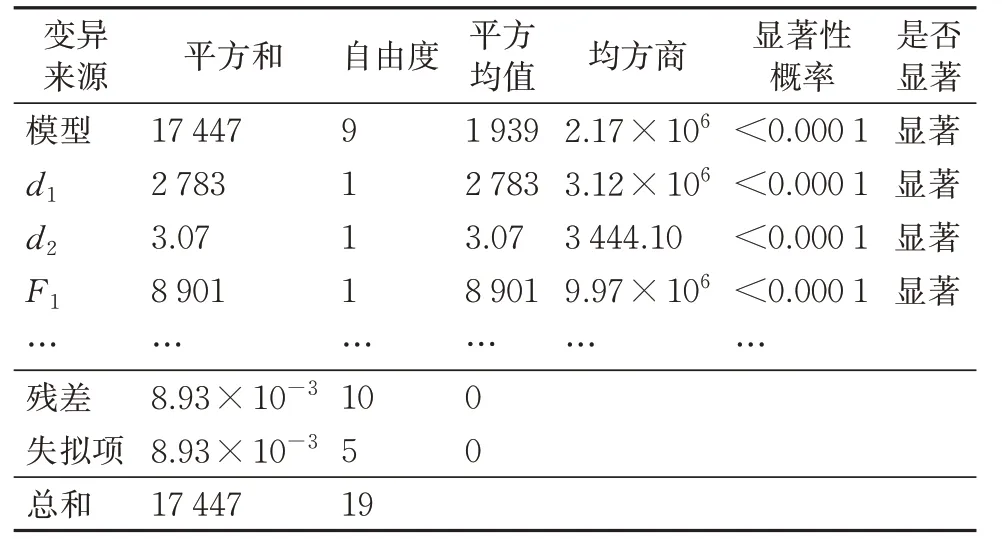
表5 工况1下构架静强度响应面函数ANOVA结果
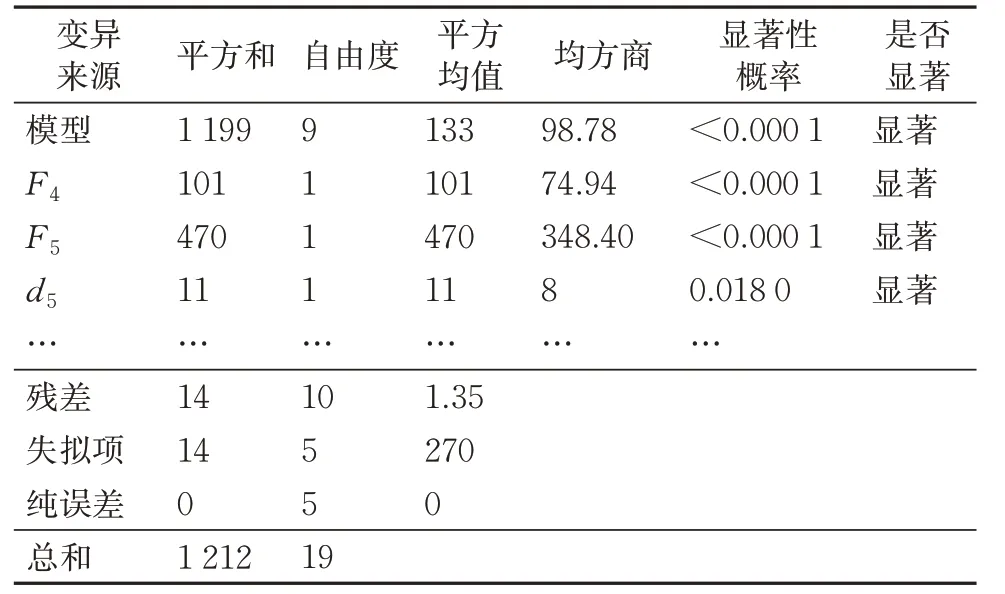
表6 工况4下构架静强度响应面函数ANOVA结果
通过方差分析可知,以上列举的2个工况下构架的响应面函数拟合精度较高,可以用于表征不确定性设计参数与输出的响应函数间的关系;且各设计参数的显著性较为明显,验证了不确定性设计参数选择的合理性。
2.3 构架失效概率响应面代理模型的建立
根据文献[18]确定每层样本个数和初始条件概率的取值范围,对构架进行D-最优试验设计。基于式(10)—式(13)、表3和试验设计,采用SS方法求解对应的失效概率,其中工况1和工况4下的试验设计结果分别见表7和表8。

表7 工况1下构架D-最优试验设计及响应值
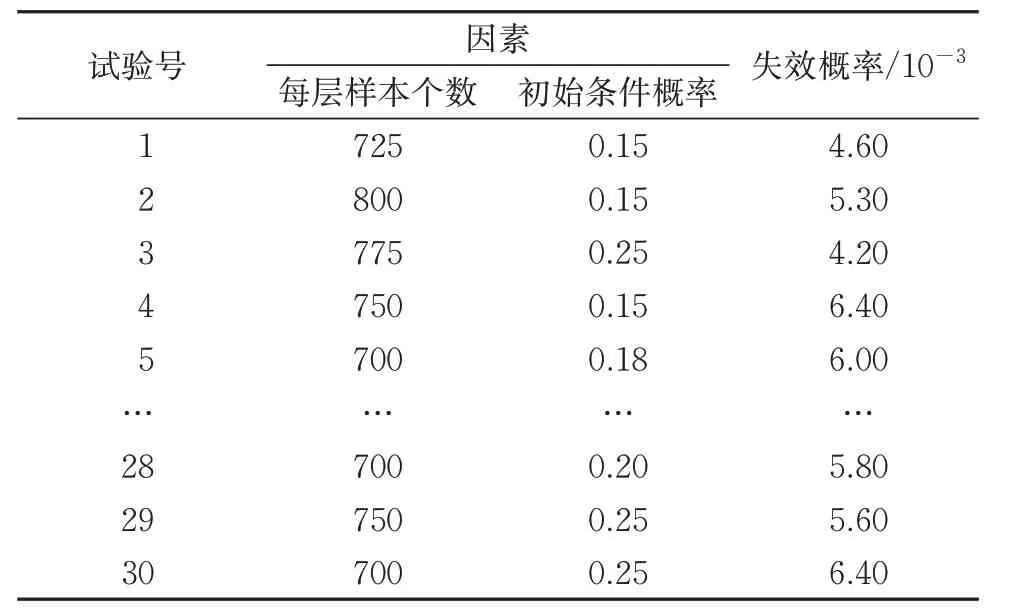
表8 工况4下构架D-最优试验设计及响应值
采用麦夸特法对各工况下试验数据进行插值拟合,得到每层样本个数和初始条件概率关于失效概率的高阶响应面代理模型,如图3所示。为验证构架失效概率响应面模型的拟合精度,得到试验值与预测值的残差分布如图4所示。图4中:样本点表示由试验设计得到的试验值,灰色平面表示响应面的预测标准面。
由图3可知:每层样本个数和初始条件概率的不确定性对失效概率的影响较大,虽然与SS 方法的基本表达式相吻合,但是在采用SS方法过程中,依据经验确定每层样本个数和初始条件概率取值范围,由此计算得到的失效概率未必最优,降低了可靠性分析的精度。因此,寻求最优的每层样本个数和初始条件概率取值范围,对确定最优失效概率、保证可靠性分析的准确性具有重要的意义。

图3 不同工况下P0和N关于PL的响应面代理模型

图4 不同工况下响应面代理模型的残差分布
由图4可知:各工况残差的数量级均为10-4,说明响应面代理模型的拟合精度较高,可用于后续的最优失效概率的求解。
3 基于IDEPSO-SS的单工况下构架可靠性分析
3.1 IDEPSO算法最优控制参数的确定
在IDEPSO算法中,缩放因子J、变异概率P、种群规模M及惯性权重的最大值ωmax和最小值ωmin等控制参数对其优化的效率和精度具有显著的影响[19]。为此,采用正交试验设计获取IDEPSO算法最优的控制参数组合。各控制参数及其水平值见表9,正交试验表L25(55)见表10。

表9 不同水平下IDEPSO算法控制参数值
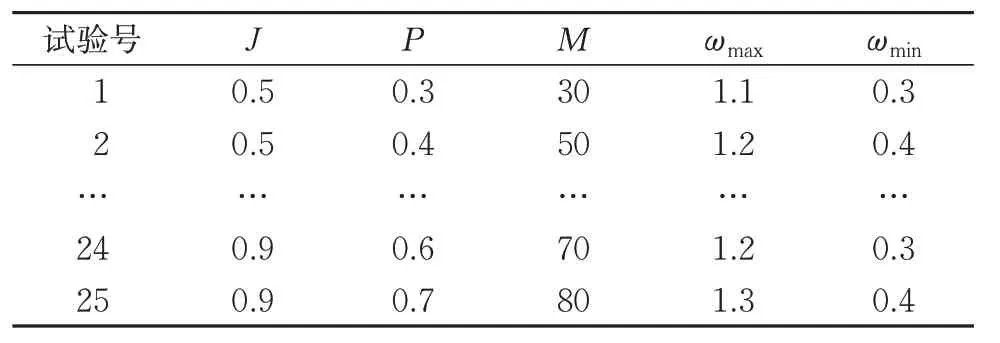
表10 各控制参数正交试验设计值
为验证IDEPSO算法的求解精度,基于图3所示各工况下高阶响应面代理模型计算得到的失效概率,并将其与MCS的差值定义为适应度函数。将表10中的数据代入IDEPSO算法中,对适应度函数进行寻优,并对正交试验设计结果进行分析,得到各工况下最优控制参数水平组合分别为:J=0.6,P=0.4,M=50,ωmax=1.3,ωmin=0.3;J=0.7,P=0.7,M=30,ωmax=1.5,ωmin=0.3;J=0.7,P=0.7,M=50,ωmax=1.2,ωmin=0.4;J=0.7,P=0.3,M=30,ωmax=1.1,ωmin=0.3。
3.2 构架单工况下最优失效概率计算
采用各工况下最优控制参数再次对适应度函数进行优化,得到各工况下最优失效概率及每层样本个数和初始条件概率。不同优化算法下各工况的迭代曲线如图5所示。图中:GA为遗传算法;GAPSO为遗传算法优化的粒子群算法。
由图5可知:各工况下每层样本个数和初始条件概率的最优值分别为(805,0.25)(803,0.26)(801,0.11)和(770,0.182),可见由于适应度函数不同,得到的每层样本个数和初始条件概率最优值也不同,若按照经验对其取值得到的失效概率很难保证最优;与GAPSO,PSO 和GA算法比,IDEPSO算法在收敛速度和精度上最优,尤其在收敛速度上具有明显优势,同时避免了优化过程陷入局部最优解的情况。
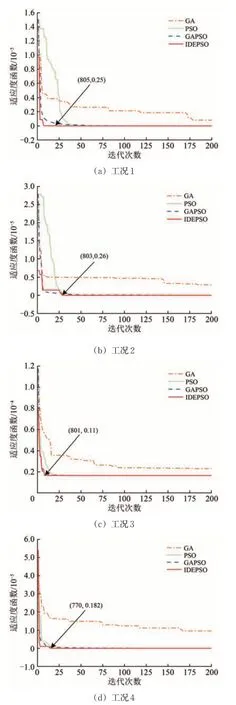
图5 不同优化算法下各工况的迭代曲线
各工况下基于最优失效概率的构架累积分布函数如图6所示。IDEPSO-SS算法与MCS算法的结构失效概率(模拟精度)和调用函数次数(模拟效率)对比分别见表11和表12。

图6 各工况下基于最优失效概率的构架累积分布函数
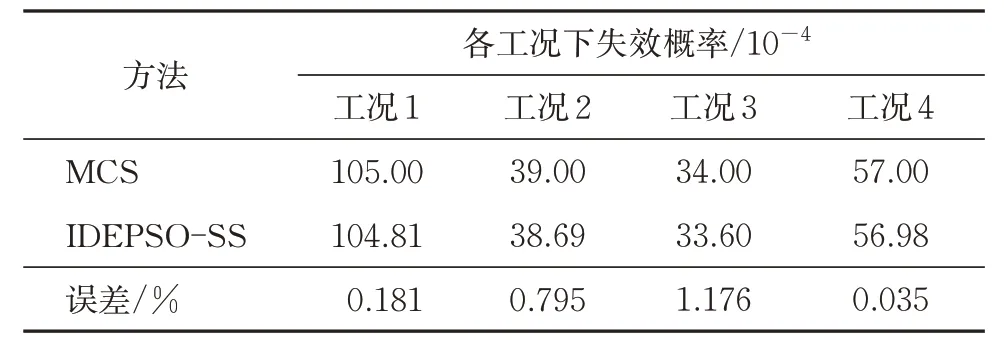
表11 IDEPSO-SS与MCS精度对比

表12 IDEPSO-SS与MCS效率对比
由表11和表12可知:与采用MCS算法相比,采用IDEPSO-SS算法得到的最优失效概率误差较小,精度较高,且计算效率显著提高,可以较为准确地表示构架在设计参数波动下的可靠性水平。
4 多工况下构架可靠性分析及最优失效次序确定
多工况结构可靠性分析的前提是获得各工况的联合失效概率。为分析相关系数对失效概率的影响,将图6得到的最优失效概率代入式(7)和式(8),计算得到相关系数ρ≥0.6时各工况下的联合失效概率,计算结果见表13。
根据表11和表13,采用Ditlevsen 方法计算多工况下构架的结构可靠度,并利用最优准则法确定最大下界及结构最优失效次序,计算结果如图7所示。图中:阴影部分为相关系数取0.6~0.9时多工况下构架失效概率界宽。
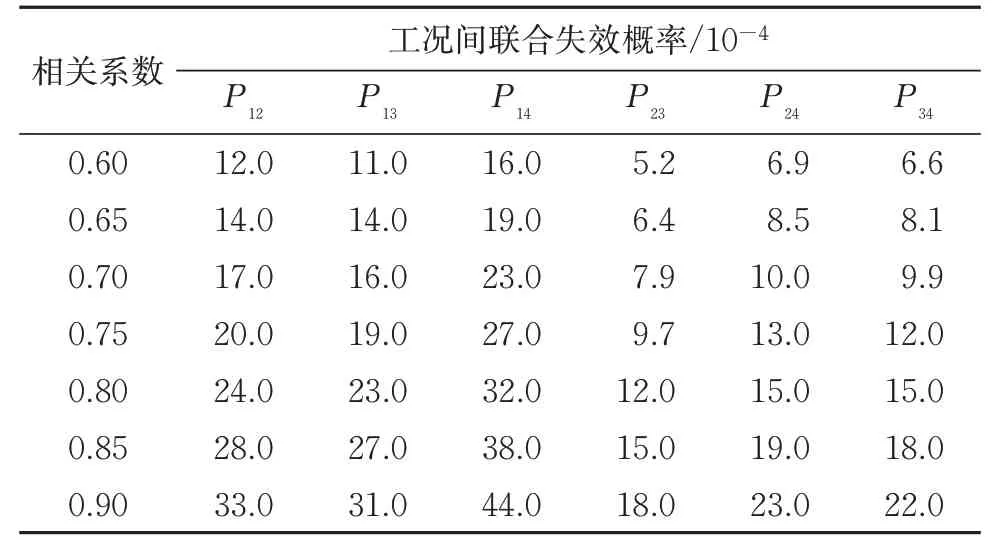
表13 各相关系数下工况间联合失效概率
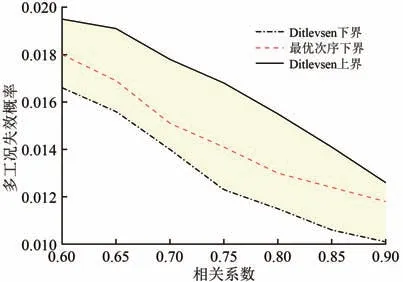
图7 多工况下构架可靠度
由图7可知:随着相关系数的增加,失效概率呈现下降趋势,表明考虑各工况间的相关性后,各工况类似于并联系统,导致失效概率降低;优化得到的失效概率界宽较窄,说明最优失效次序下的可靠度计算结果较为保守,降低了在设计阶段按照工况顺序依次失效导致过高估计结构可靠度的风险。对比图6可知,单工况的结构可靠度均高于多工况结构可靠度,表明仅进行单工况可靠性分析,计算结果过高,设计偏于危险。
相关系数ρ=0.6时最优准则法的求解过程见表14。表中:*代表构架各工况的最优失效次序。

表14 相关系数为0.60时最优准则法求解过程
由表14可知,采用最优准则法得到的最优失效次序为工况1、工况4、工况2 和工况3,基于该次序计算得到的最优可靠度减少了Ditlevsen 方法的界宽,而且偏于安全。
5 结 论
(1)采用IDEPSO算法优化SS的每层样本个数和初始条件概率,提出基于改进SS 方法即IDEPSO-SS的单工况下最优失效概率计算方法,并且将其与Ditlevsen 方法、最优准则结合,提出多工况下最优可靠度及最优失效次序计算方法。
(2)采用IDEPSO-SS算法对转向架构架进行单工况下的可靠性分析,得到各工况下的最优失效概率。通过与传统方法对比,表明采用IDEPSOSS算法在保证计算精度的前提下,计算效率明显提高。
(3)构架的多工况下可靠性分析实例表明,本文方法较单工况下的可靠性分析,结果不仅更贴近工程实际,而且更加安全;获得的最优失效次序有利于获得结构在多种组合工况下的最优可靠度,为提高轨道车辆关键零部件的设计水平,保证可靠性分析的准确性提供了方法支撑。

