考虑弹性车体的轨道车辆转向架悬挂参数多目标优化设计

肖 乾，罗佳文，周生通，李 超，罗志翔，郭冰彬

（1.华东交通大学 载运工具与装备教育部重点实验室，江西 南昌330013；2.中车株洲电力机车有限公司 大功率交流传动电力机车系统集成国家重点实验室，湖南 株洲412001)

随着我国轨道车辆运营速度的提高，车辆运行的平稳性和舒适性日益受到人们的关注。由一系和二系悬挂组成的转向架悬挂系统是连接轮对与车体的重要部件，合理的转向架悬挂参数对轨道车辆动力学性能有着重要的影响。因此，优化转向架的悬挂参数就显得尤为必要。

国内外学者对转向架悬挂参数优化进行了大量的研究。Shieh N C 等[1]采用多目标优化算法，对轨道车辆悬挂系统的弹簧刚度、阻尼参数进行了优化设计，车辆垂向运行平稳性能得到很大的提升。Ashtiani I H[2]基于UM 软件建立了三大件式转向架货车的刚体动力学模型，以重载和空载情况下货车车体垂向振动加速度最小为优化目标，对斜锲的几何形状进行了优化。朴明伟等[3]以拖车为研究对象，在对车辆振动舒适性进行型式试验和仿真的基础上，研究空气弹簧对车辆垂向振动舒适性和地板振动的影响。李响等[4]基于SIMPACK 软件建立考虑弹性轮对和弹性构架的刚柔耦合动力学模型，但并没有将车体考虑为柔性。东方世平和于大方[5-6]建立SIMPACK 软件与Isight 软件的联合仿真接口，采用遗传算法对转向架悬挂参数进行优化设计，优化后车辆动力学性能有所提升。解欢等[7]研究建立了以车辆动力学性能为目标函数的轨道车辆悬挂参数优化模型，基于此使得车辆运行性能得到明显改善。薛廉政[8]基于矩阵缩减法，采用ANSYS 和SIMPACK 软件建立某拖车刚柔耦合模型，对转向架悬挂参数进行优化。尽管国内外学者针对转向架悬挂参数的优化做了大量的研究，但大多数学者只基于车辆多刚体动力学模型进行转向架悬挂参数优化；少数学者虽基于矩阵缩减理论提取整备车体模态，采用SIMPACK 和ANSYS 软件建立车辆-轨道刚柔耦合模型进行悬挂参数优化，但由于矩阵缩减法只能生成近似的质量矩阵和阻尼矩阵[9]，计算结果存在一定误差。

本文以最高运营速度为160 km·h-1的某地铁列车的头车为研究对象，采用有限元软件HYPERMESH 和ANSYS，基于Craig-Bampton 固定界面模态综合法[10]（简称C-B法），在多体动力学软件Universal Mechanism（简称UM）中建立基于弹性车体的车辆-轨道刚柔耦合动力学模型；在此基础上，采用多学科优化软件Isight，以车辆运行时车体地板面上的车体前端、中部、后端的平稳性指标为优化目标，以脱轨系数、轮重减载率、轮轨垂向力、轮轴横向力为约束条件，对转向架悬挂参数进行多目标优化设计。

1 优化理论基础

1.1 刚柔耦合动力学理论

弹性车体的坐标系由整体坐标系和浮动坐标系组成。在整体坐标系（SC0）中，浮动参考坐标系（SC1）上某一节点k的位置矢量rk为

式中：r01为SC1 原点至SC0 原点的位置矢量；A01为SC1原点至SC0原点的转化矩阵；u1-k为弹性车体变形后节点k在SC1中的径向量。

u1-k由弹性车体变形前节点k在SC1 中的相对变形矢量d1-k和径向量ρ1-k共同决定，即

弹性车体上任意点的弹性变形矢量可以通过有限元法和模态法求得，节点在SC1 中的坐标用模态矩阵与模态坐标的乘积表示，为

式中：v为（N×1）维的节点坐标，其中N为车体有限元模型自由度的总和；hi为第i阶模态；li为第i阶模态对应的模态坐标；H为模态矩阵（静力模态和约束模态的组合）；l为模态位移。

节点k的应力σk为

其中，

ε=Dv

式中：D为弹性矩阵。

在多体动力学软件UM 中采用C-B 法模拟复杂的弹性体模型，则弹性车体的特征模态可由下式求出。

式中：C为刚度矩阵；λ为特征值；M为质量矩阵；y为特征模态。

1.2 多目标非劣排序遗传算法NSGA-Ⅱ

地铁车转向架悬挂参数多目标优化问题的数学模型为

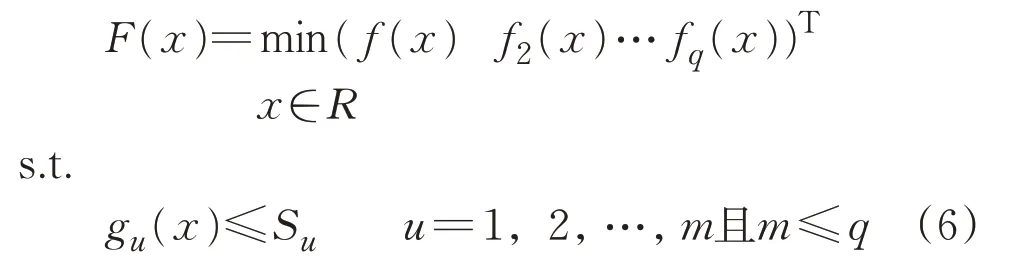
式中：F(x)为目标函数，表示车辆动力学性能指标值；x为设计变量，表示转向架各悬挂参数；q为变量个数；gu(x)为约束函数，表示车辆的脱轨系数、轮重减载率、轮轨垂向力、轮轴横向力等安全性指标；Su为约束值；R为转向架各悬挂参数的取值范围。

对多目标优化问题求解时，常采用NSGA，MOGA，SPEA，NPGA 等遗传算法进行多目标优化求解。本文采用第二代非劣排序遗传算法NSGA-Ⅱ算法[11]进行优化求解计算，该算法不仅降低了非劣排序遗传算法的复杂性，且算法本身运行速度快、收敛性好。在进化过程中，各参数定义如下[12]。

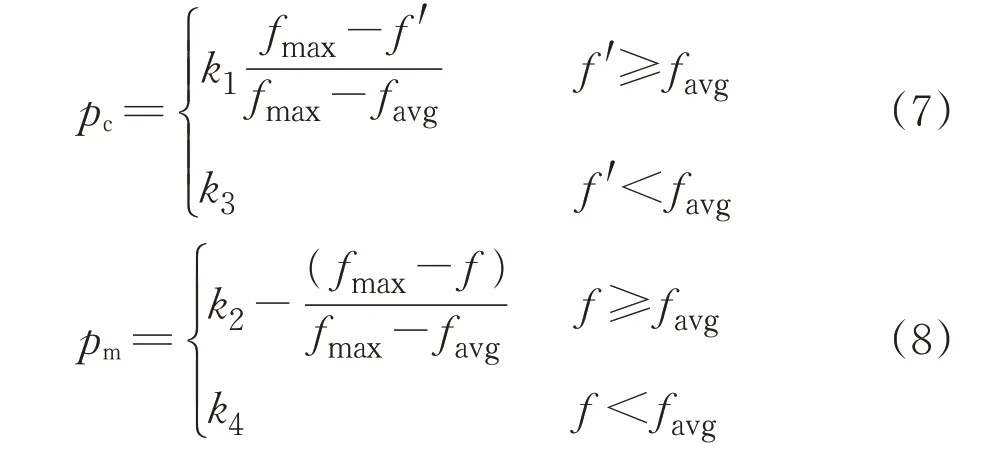
式中：pc，pm分别为交叉概率和变异概率；k1-k4为小于1的常数；f′为2个交叉个体中较大的适应度函数值；f为需要变异的个体适应度函数值；fmax和favg分别为悬挂参数优化过程中最大的适应度函数值和平均适应度函数值。

2 车辆-轨道刚柔耦合动力学模型

研究的某地铁头车车体模型由司机室、侧墙、端墙、顶盖、底架和车载设备等结构组成。在三维软件UG 中建立纯车体的三维实体模型，再导入有限元软件HYPERMESH 中建立的车体有限元网格模型，模型采用四节点板壳单元进行离散。以车体空气弹簧安装点作为界面节点，在ANSYS 软件中通过固定界面模态综合法将车体模态等相关信息导入UM软件中，得到弹性车体模型。车载设备包含辅助制动、低压箱、辅助变流器、空调、开闭机构、贯通道、车门、防爬器、全自动车钩、半自动车钩等，总质量约8.314 t。辅助风缸、辅助制动、低压箱等车下设备安装在车底横梁上，仿真时将它们整体视为悬挂梁。为了使整备车体建模精确，在UM 软件中将悬挂梁、辅助变流器、空调等质量较大的设备考虑成刚体，通过弹簧阻尼系统与车体底架相连；其他小质量车载设备在UM 软件中只考虑其质量，刚性悬挂在悬挂梁或吊脚处。在UM动力学模型中，轮对模型采用自带的轮对子系统模块建立，对于轮对构架之间的一系悬挂，一系垂向减振器采用以线性力元（Linear）模拟，一系钢簧采用线性黏弹性力元（Viscous-elastic）模拟，轴箱转臂节点采用衬套力元（Bushing）模拟；对于构架与车体之间的二系悬挂，二系横向减振器、二系垂向减振器、二系空气弹簧均采用Viscous-elastic 力元模拟，牵引拉杆采用Linear力元模拟，抗蛇行减振器采用非线性的黏弹性力元（Nonlinear Viscouselastic）模拟，抗侧滚扭杆和横向止挡采用Bushing 力元模拟。为了更真实地模拟车载设备与车体连接，采用Bushing 力元模拟此连接方式。轨道模型采用UM 自带的Massless 轨道，并以UIC-good轨道谱作为轮轨之间的激励，其不平顺如图1所示。

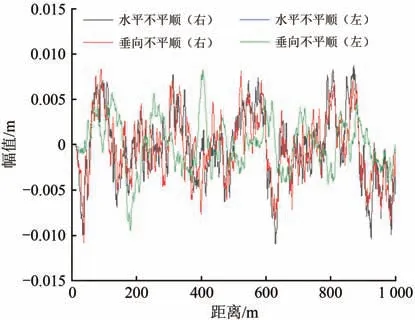
图1 轨道不平顺

最终建立整备状态下车辆-轨道刚柔耦合系统动力学模型，如图2所示，整个模型由44个刚体自由度和14阶弹性车体自由度组成。

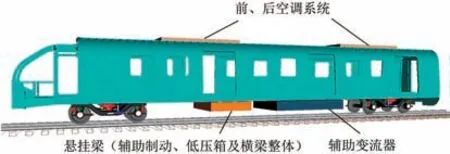
图2 基于弹性车体的车辆-轨道刚柔耦合系统动力学模型

采用C-B 法计算模型的模态时，只选用子结构的低阶模态进行计算，因此，为了验证弹性车体模型的准确性，需要对车体有限元模型进行模态分析。使用ANSYS软件中Block Lanczos特征值求解器提取车体前20阶自由模态，去除前6阶刚体自由模态，计算得到的车体自由模态，与通过ANSYS_UM.EXE 接口正则化后转换成弹性车体的正则化后模态对比见表1。

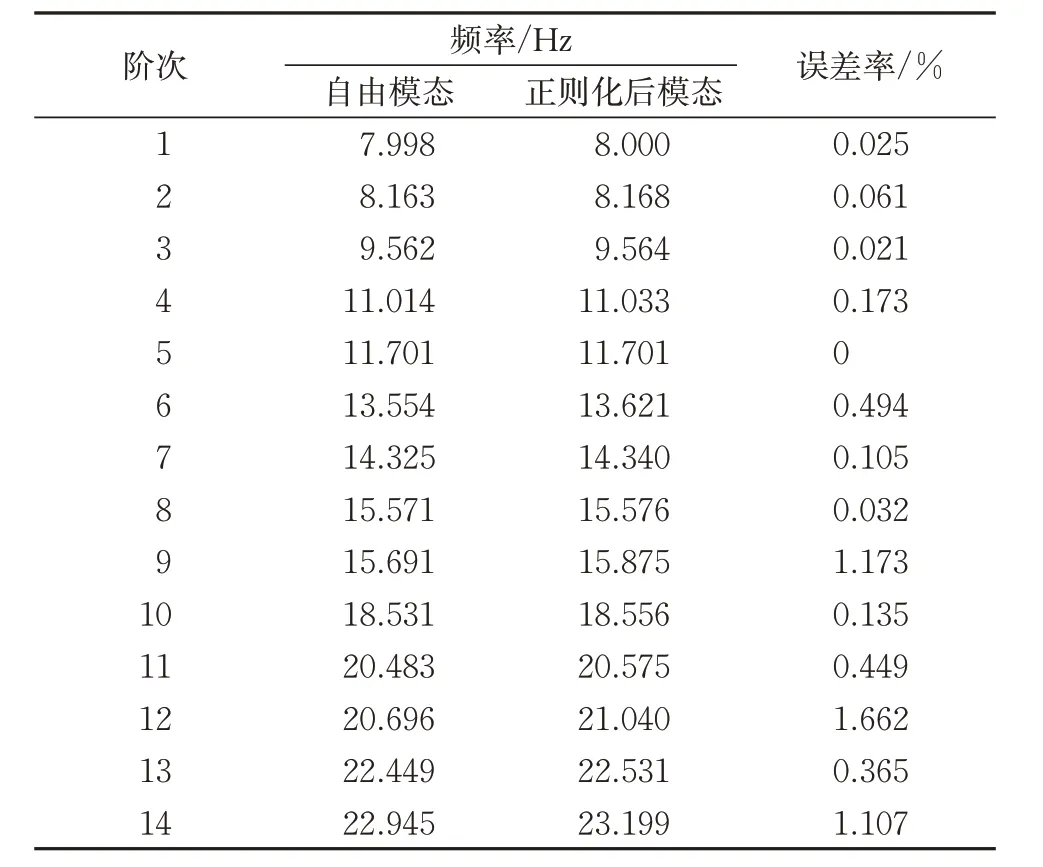
表1 模态对比

从表1可以看出：自由模态与正则化后模态的频率相差较小，最大误差处于2%之内，能够用于指导工程实践，同时表明建立的弹性车体模型准确性较高。

3 弹性车体对车辆平稳性影响

已有研究表明，轨道车辆的一系、二系悬挂刚度和悬挂阻尼等参数对车辆平稳性有较大影响[13-14]。除此之外，车体的弹性振动也是影响车辆平稳性的重要因素[15]。车辆-轨道刚柔耦合动力学模型车辆和多刚体动力学模型最大的区别在于前者考虑了车体的弹性振动，尽管前文在建模时引入了前14阶车体模态，但是为探究车体弹性振动对转向架与车体之间耦合振动的影响，还需对比分析2种动力学模型在直线工况下车体前端和后端的平稳性指标，结果分别如图3和图4所示。计算时，振动加速度测点位置根据GB/T 5599—2019《机车车辆动力学性能评定及试验鉴定规范》要求进行设置。

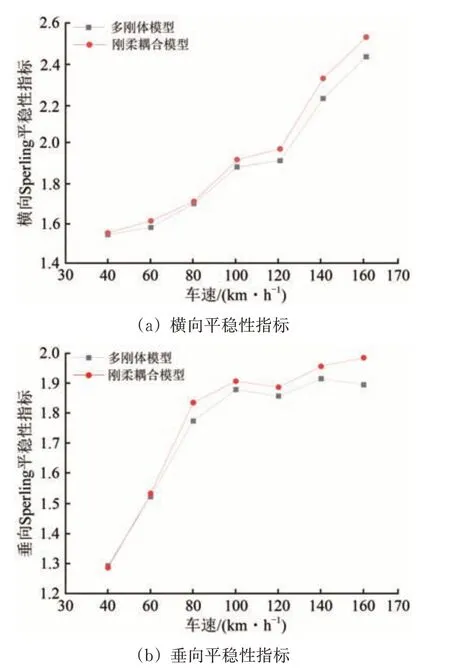
图3 车体前端平稳性指标对比

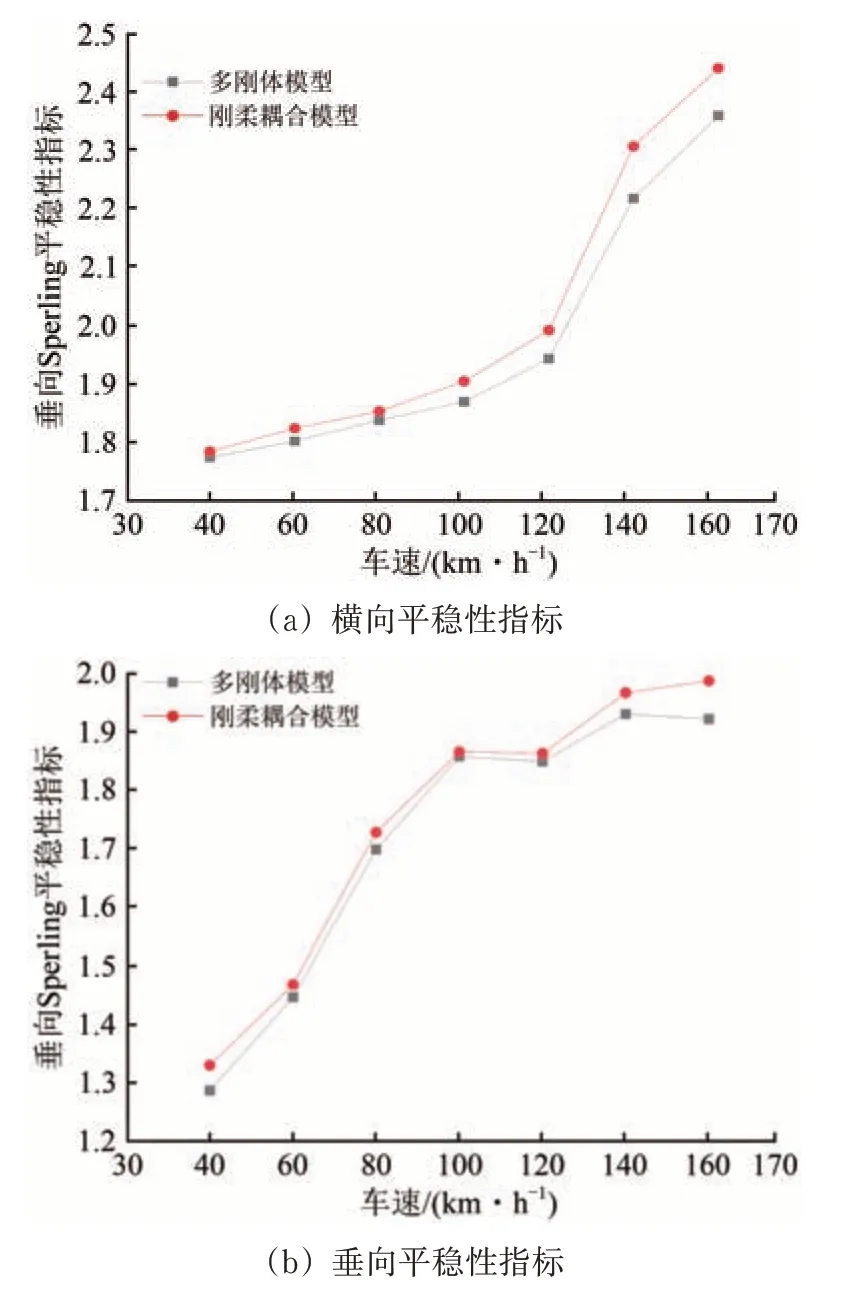
图4 车体后端平稳性指标对比

从图3和图4可以看出：同种外部条件激励下，车辆-轨道刚柔耦合动力学模型的平稳性指标整体上要大于车辆多刚体动力学模型；在车速小于80 km·h-1的低速直线工况下，车辆的横向和垂向平稳性指标相差不大；当车速大于80 km·h-1时，车体的弹性振动作用较为明显，车辆-轨道刚柔耦合动力学模型的平稳性指标明显大于多刚体动力学模型，且速度越大趋势越明显，说明车体的弹性振动对车辆的运行性能有一定影响，且影响程度随车辆运行速度的提高而加大。

4 转向架悬挂参数优化

4.1 优化平台搭建

选取一系和二系弹簧水平、垂向刚度，一系垂向阻尼及二系垂向和横向阻尼等悬挂参数作为设计变量，并以设计原型车时的初始值为基准，上下浮动30%作为设计变量取值范围的上限和下限，以进行试验设计。设计变量及其取值范围见表2。

表2 设计变量及其取值范围

最优拉丁超立方法具有良好的空间填充能力，相较于其他设计方法，在精度相仿的情况下所需样本点大量减少且拟合非线性响应能力强，设计空间样本点分布也更均匀。因此，采用最优拉丁超立方法设计试验样本。

样本的数目一般为几十到数千不等，这里选择的样本点数为380 组。若将每组样本点导入UM 软件计算且手动记录车辆的平稳性、脱轨系数等数据耗费将大量时间。此时可建立Isight 软件与UM 软件的联合仿真平台，利用Isight 软件控制UM 软件的自动计算，并自动保存计算的结果。Isight 软件与UM软件没有直接的接口，联合仿真需满足以下2个条件：①仿真模型文件可读且能实现自动计算；②结果文件可读。因此只需借助Matlab 软件编写相应程序，将UM 软件输出的二进制格式结果文件转变为Isight可读取的十进制格式文件，即可完成联合仿真。

通过Isight 软件与UM 软件的联合仿真平台完成最优拉丁超立方样本点的计算，可以得到各组样本中悬挂参数组合对应的如平稳性、脱轨系数等响应数据，进而得到1个基于设计变量取值范围的局部最优悬挂参数组合。但若想得到全局最优解则需要扩大设计变量的取值范围，计算更大规模的样本点。车辆-轨道刚柔耦合系统动力学模型在仿真时需计算大量的非线性微分运动方程组，计算难度大且时间久，而代理模型能减少计算和分析的复杂度，因此选用代理模型近似替代刚柔耦合动力学模型[16-17]。Isight软件自带有多种类型代理模型生成功能，可利用已计算的样本点数据，采用径向基函数神经网络代理模型技术进代理模型行建模[18]，并利用多目标遗传算法NSGA-Ⅱ对车辆转向架悬挂参数进行寻优计算，优化流程如图5所示。

车辆的仿真运行工况参考相关国家标准进行设置，其中直线工况运行速度为160 km·h-1、运营里程为1 000 m，曲线有3种运行工况，每种工况运营里程均为1 200 m，曲线工况其他参数具体见表3。

4.2 多目标优化计算

利用NSGA-Ⅱ遗传算法，设置优化的代数为80次，每代的个体数为60个，对车辆转向架悬挂参数进行寻优计算。优化计算共进行4 800次，优化得到的所有个体均满足标准GB/T 5599—2019《机车车辆动力学性能评定及试验鉴定规范》规定的安全限值。从优化结果中选取7 组通过NSGA-Ⅱ算法求解的最优悬挂参数，取值见表4。

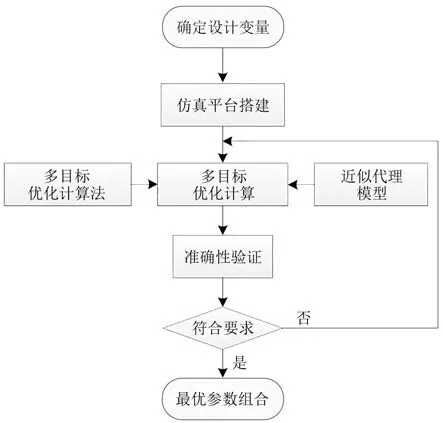
图5 转向架悬挂参数优化流程

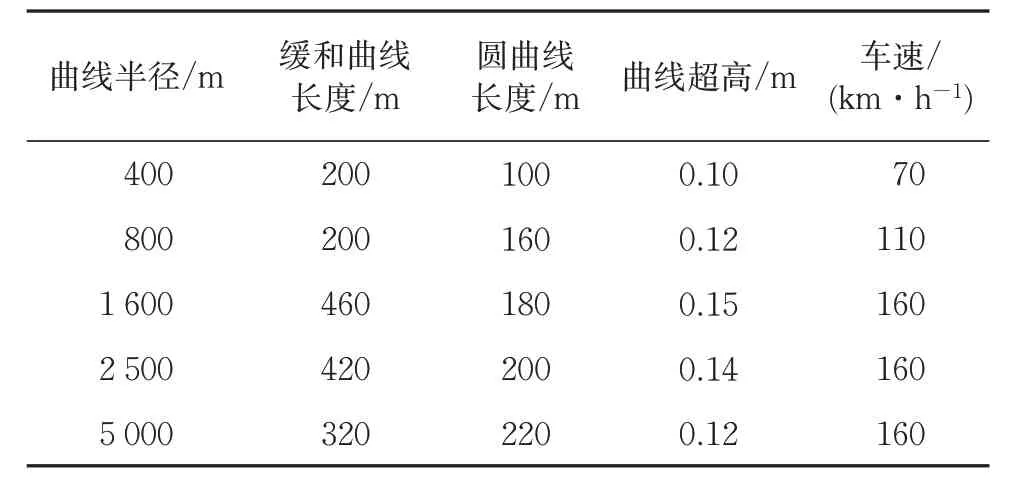
表3 曲线工况仿真参数

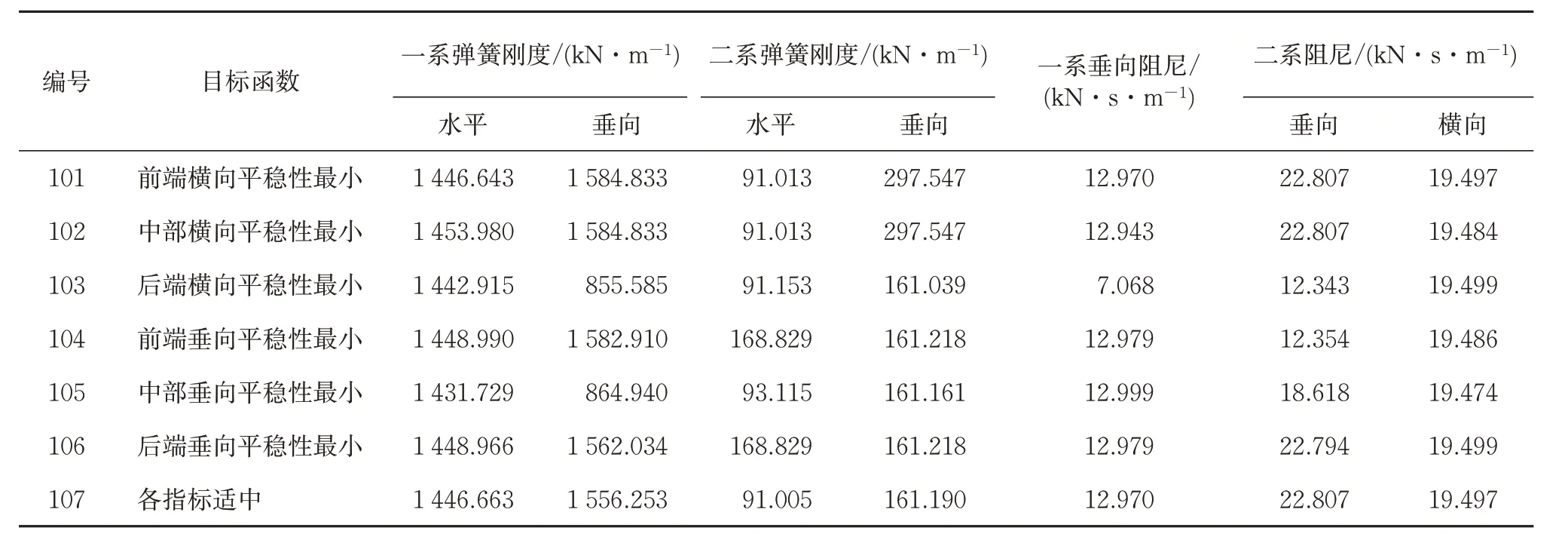
表4 典型优化设计点及对应悬挂参数

为验证通过代理模型求解地铁列车车辆动力学性能的准确性，分别将以上7 组悬挂参数写入UM软件的车辆-轨道刚柔耦合模型文件中，进行动力学仿真计算。悬挂参数优化后代理模型输出的平稳性指标预测值和UM软件实际仿真得到的平稳性指标计算值以及优化前平稳性指标计算结果即其初始计算值对比见表5，对预测值与计算值二者之间相对误差的分析结果见表6。

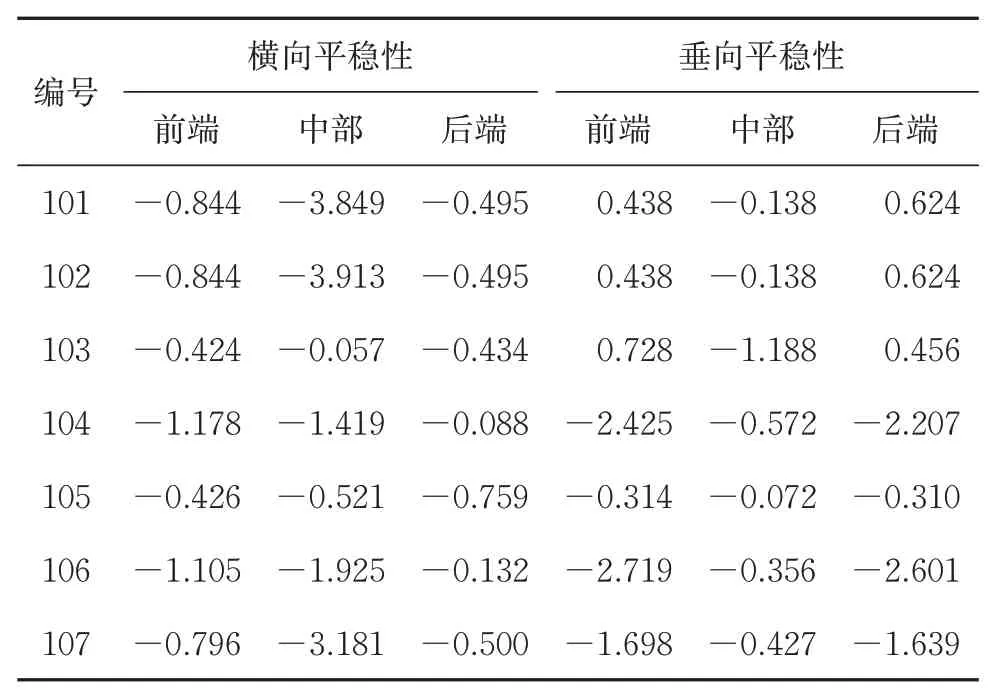
表6 典型优化设计点不同平稳性指标预测值与计算值相对误差 %

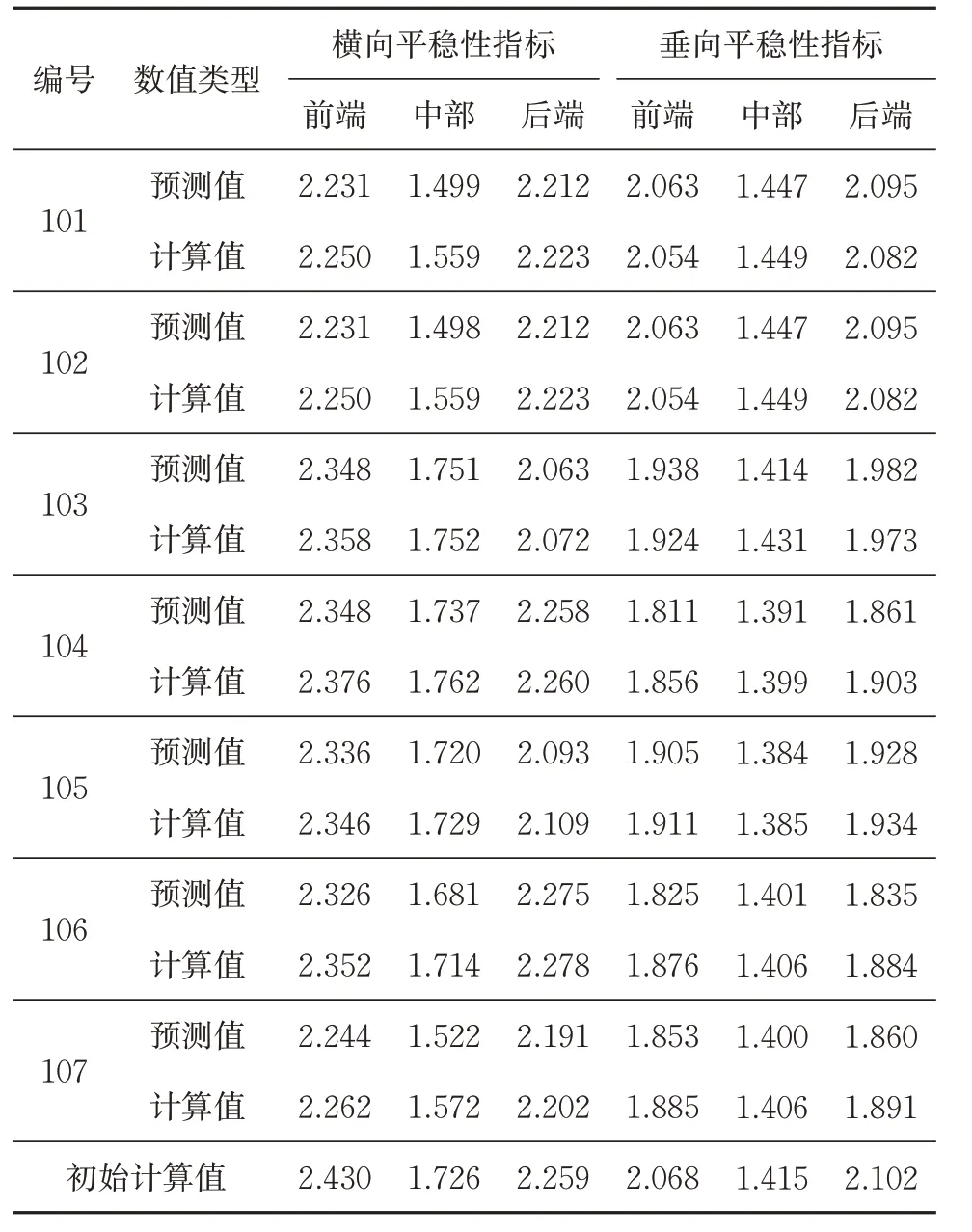
表5 典型优化设计点预测值与实际值对比

从表5可以看出：编号101—107 这7 组悬挂参数，代入车辆仿真模型中计算得出的横向和垂向平稳性指标与优化前计算的结果相比，均有不同程度的减小。

从表6可以看出：优化计算得到的最优解动力学指标预测值与仿真获得的计算值相差很小，各动力学指标相对误差均不超过4%，这表明优化计算结果的准确性较高，同时也进一步表明采用代理模型代替车辆-轨道刚柔耦合模型进行计算的准确性较高。

为确定最佳的转向架悬挂参数，使车辆运行平稳性指标处于最佳状态，将最优解编号求解出的目标函数预测值与采用初始悬挂参数获得的目标函数初始计算值进行对比分析，计算出预测值较初始计算值的优化率，结果见表7。

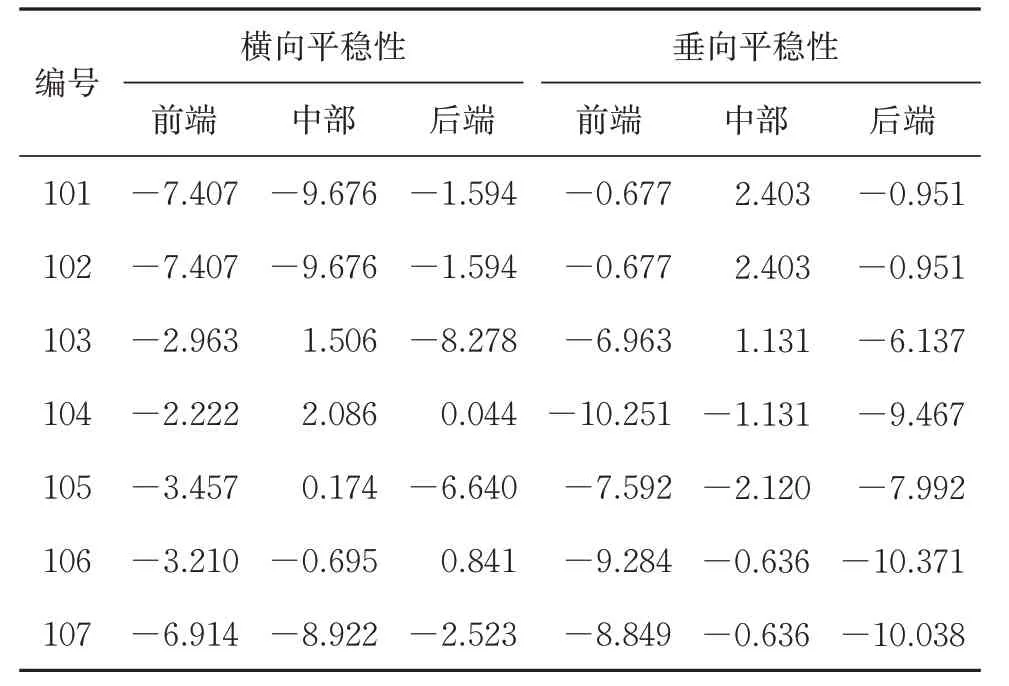
表7 典型优化设计点不同目标函数预测值较初始计算值优化率 %

从表7可以看出：悬挂参数优化后的车辆相比原始车辆，直线运行平稳性能显著得到提升，且个别指标优化幅值在10%以上；相比于107编号所求出的动力学指标，其他典型编号下求出的动力学特性都存在某一指标值相比初始值增大的现状，并且在107 编号下的车体前端、中部和后端垂向平稳性指标优化率分别达8.849%，8.922%和10.038%，优化效果明显。

综上分析可知，悬挂参数的最优值为编号107对应的车辆转向架悬挂参数值，即一系弹簧水平刚度为1 446.663 kN·m-1、垂向刚度为1 556.253 kN·m-1，二系弹簧水平刚度为91.005 kN·m-1、垂向刚度为161.190 kN·m-1，一系垂向阻尼为12.970 kN·s·m-1，二系垂向阻尼为22.807 kN·s·m-1、横向阻尼为19.497 kN·s·m-1。

将编号107 所对应的车辆悬挂参数，代入动力学软件UM 中计算出其各曲线工况下的脱轨系数、轮重减载率、轮轨垂向力、轮轴横向力的最大绝对值，并与优化前对比见表8。由GB/T 5599—2019《机车车辆动力学性能评定及试验鉴定规范》的评定标准得到曲线工况下车辆各动力学指标的允许限值，其中轮轨垂向力的最大绝对值是170 kN，轮轴横向力的最大绝对值是46.802 kN，而脱轨系数第二限度的最大绝对值为1.0，轮重减载率第二限度的最大绝对值为0.6。从表8可以看出：优化前后的车辆均符合安全性要求。

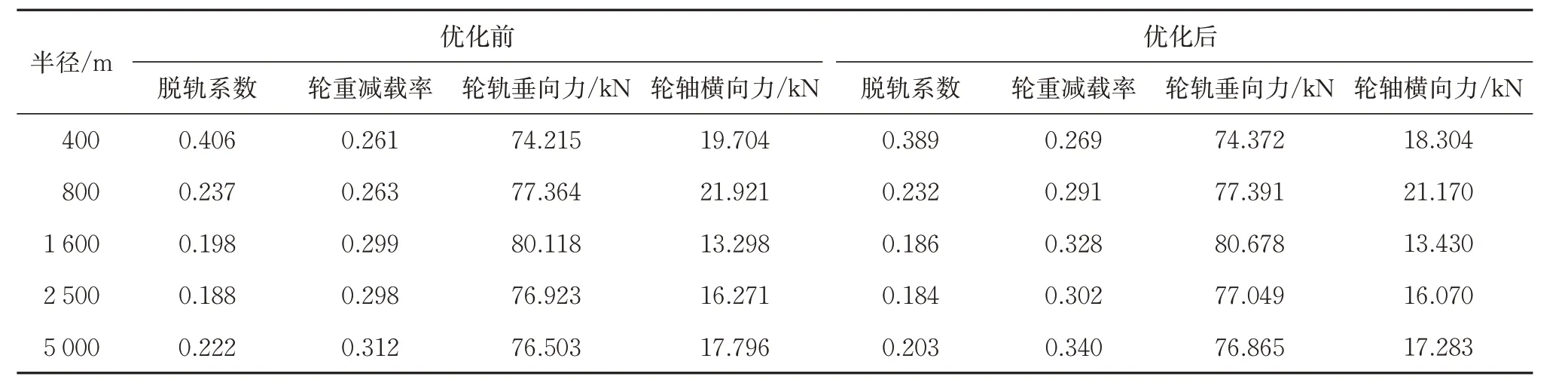
表8 曲线动力学应能优化前后对比

5 结 论

（1）相对于传统的仅考虑单一目标的优化方法，利用最优拉丁超立方试验技术、径向基函数神经网络代理模型技术和多目标遗传算法NSGA-Ⅱ，对转向架悬挂参数进行多目标优化设计时，能综合考虑各悬挂参数对车辆各项动力学性能的影响，得到全局范围内最优的悬挂参数组合。

（2）相同工况下，车辆刚柔耦合模型的平稳性指标整体上要大于多刚体动力学模型，且随着速度的增大，二者差异有加大的趋势，说明车体的弹性振动对车辆的运行性能有一定影响，且影响程度随着车辆运行速度的提高而加大。

（3）通过分析车辆转向架悬挂参数的多目标优化结果可知，优化后车辆动力学特性得到显著改善，车体前端、中部和后端垂向平稳性指标优化率分别达8.849%，8.922%和10.038%。