基于智能算法的空冷火电机组负荷预测研究

彭维珂，聂椿明，陈衡，徐钢

（华北电力大学能源动力与机械工程学院，北京102206）

0 引言

我国煤水资源分布不均严重制约了富煤贫水地区火电的发展。直接空冷机组以环境空气为冷源来吸收汽轮机的排汽热量，相比于同容量的湿冷机组，空冷机组冷却系统本身可节水95%以上，全厂可节水约65%，节水效果显著［1］。“十二五”以来，我国空冷技术得到了长足发展，机组数量和装机容量均处于世界前列。

由于并网机组形式复杂繁多，负荷需求变化较大，电网侧的调度指令往往和机组实际负荷之间存在较大偏差［2］，严重影响机组运行的安全性与经济性。因此，要得到单台机组实际负荷指令的预测值，应从机组本身开展深入研究。

目前，针对燃煤机组负荷预测的研究已经引起了国内外学者的广泛关注。骆小满等［3］运用神经网络算法，建立了基于冀北某热电联产机组的热-电负荷预测模型。丁伟等［2］通过对机组历史日负荷数据进行聚类分析，获取了机组负荷的相似性特征，利用历史匹配预测（HMF）算法将负荷序列和历史数据匹配，最后根据最似日负荷变化趋势来进行预测，预测结果具有较高的精度。张然然等［4］针对非正常工况，通过小波变化对负荷指令进行多尺度分析并建立差分整合移动平均自回归（ARIMA）模型，基于前N个时刻的机组负荷来进行预测并加权获取最终结果。王艳［5］在空冷温度场在线监测的基础上，采用Fortran 语言开发了直接空冷系统在线监测与分析软件。Akpan 和Fuls［6］提出了有效性检测方法来预测不同机组负荷条件下的冷凝器背压，此外还详细介绍了黑箱条件下冷凝器的性能评估方式。然而，国内外针对空冷机组负荷预测方面的研究甚少，现有研究基本停留在传统公式分析和数值模拟技术上。由于空冷机组庞大且复杂，相对于湿冷机组又存在煤耗率高、背压变化大等特点，这些预测方法均存在一定的局限性。近年来，随着智能算法的飞速发展和计算机性能的不断提升，机器学习已成为人工智能、大数据分析等领域中最具潜力的方向之一［7-8］。机器学习不强调探明各特征之间具体的物理机理，而是通过自发地从运行数据和经验中学习和改进模型，来验证输入特征与输出结果之间的潜在交互作用，实现对目标参数的预测。本文以北方某600 MW 空冷机组为研究对象，基于机组全年的历史运行数据，经过数据预处理和稳态工况筛选，分别建立反向传播（BP）神经网络预测模型和随机森林预测模型，并进行模型参数的敏感性分析。最后，通过模型输入特征筛选和分负荷工况建模，对所建立的随机森林预测模型进行性能优化。

1 案例机组概况

本文以北方某600 MW 机组为研究对象，该机组于2013年完成168 h试运行。该厂汽轮机采用超临界、三缸四排汽、一次中间再热、单轴、直接空冷凝汽式汽轮机，回热系统由3 台高压加热器、3 台低压加热器和1 台除氧器构成，机组及冷端系统布置如图1所示，基本参数见表1。

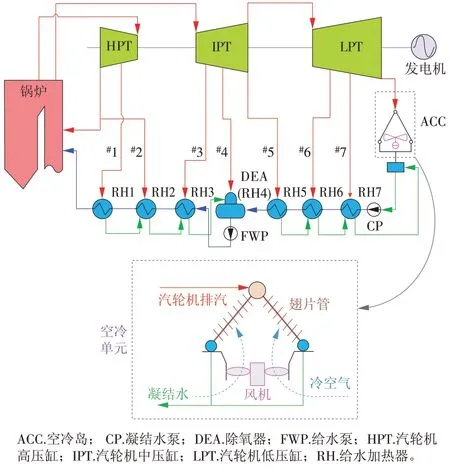
图1 案例机组及冷端系统示意Fig.1 Reference unit and its cold end system

该机组空冷岛的总散热面积为1 690 000 m2，40台顺流风机和16 台逆流风机分8 列布置于凝汽器底部。风机与其对应的空冷单元之间设置空气通道，不同冷却单元之间设置隔墙，以免相邻冷却单元相互影响和相邻风机停运而降低通风效率，机组空冷单元基本参数见表2。

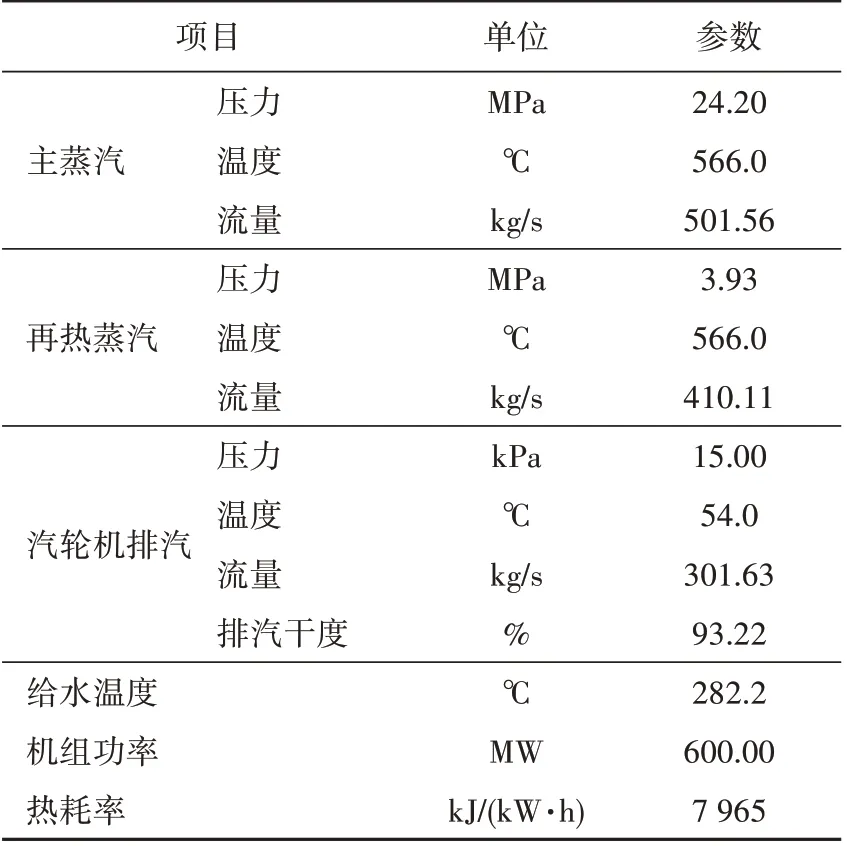
表1 案例机组基本参数Tab.1 Basic parameters of the reference unit

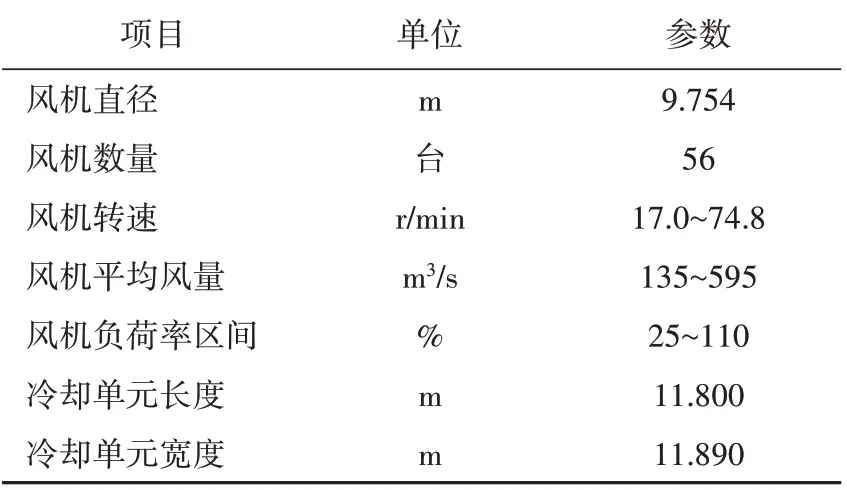
表2 案例机组空冷单元基本参数Tab.2 Basic parameters of the reference cold end system

2 数据采集和预处理

2.1 数据采集

本文选取案例机组分散控制系统中2018 年的全年运行数据作为机组负荷研究的数据集，共计1 051 200组数据，数据采集间隔为30 s，包括机组负荷、环境温度、环境风速、环境风向、风机转速、风机轴温、主蒸汽流量、主蒸汽温度、主蒸汽压力、凝结水流量、凝结水温度、凝汽器背压等12个基本参数。

2.2 数据预处理

电磁干扰、测点异常、工况变化等因素会导致运行数据中的某些测量数据缺失或偏离正常区间［9］，无法准确反映机组的实际运行状态，从而影响模型的拟合精度，因此，需要对机组原始数据进行预处理，以提升建模数据的质量。考虑到缺失数据所包含的机组信息微乎其微，为了简化数据处理流程，本文对原始数据中的缺失值采取直接剔除的处理方法；同时，根据机组和空冷岛的设计和热力试验资料，本文设置了部分运行参数的范围（见表3），参数范围外的运行数据视为异常数据或非正常运行工况，为提高下一步建模与计算的准确性，将对应工况的数据点直接剔除。

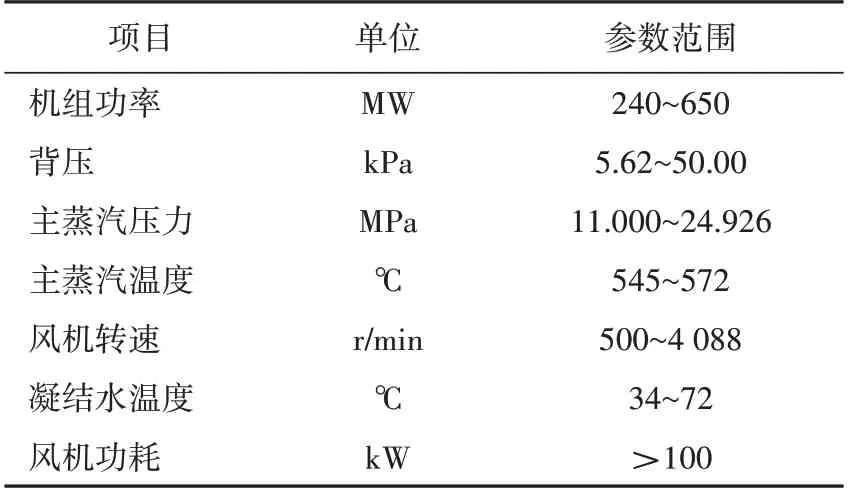
表3 案例机组运行数据参数范围Tab.3 Operation parameters'reasonable intervals of the reference unit

2.3 稳态工况筛选

电厂的实际运行是一个动态过程，机组以“稳态—过渡—稳态”的模式交替运行［9］，因此运行数据中存在大量的非稳态工况数据。非稳态工况下机组参数波动很大，监测数据不能客观地反映系统状态，因此需要引入有效的稳态监测办法来筛选工况。工业上通常采用滑动窗口法对大样本数据进行稳态工况筛选，即先将数据序列划分为有限个数据窗口，若滑动窗口的稳态判定指标小于对应阈值，则认为该窗口内的数据序列均为稳态工况，否则为非稳态工况。判断结束后直接跳入下一窗口进行判断，直至全部数据窗口判断结束。机组处于稳态工况时，有以下判别式成立［10］

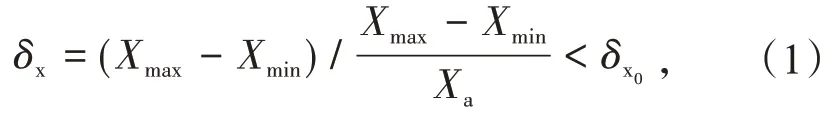
式中：δx为稳态判定指标；Xmax为滑动窗口内特征参数的最大值；Xmin为滑动窗口内特征参数的最小值；Xa为滑动窗口内所有特征参数的平均值；δx0为稳态特征判定阈值。根据稳定性判定指标与对应阈值的比较结果来判断工况状态是否处于稳态工况。

文献［10］以机组负荷、主蒸汽温度、主蒸汽压力3个特征变量作为稳态工况判别方法。考虑到空冷岛系统运行工况的复杂多变以及空冷岛参数变化的滞后性，需要增设相关的判断指标。基于精简判断指标的原则，本文最终选取机组功率、主蒸汽温度、风机群功耗和凝结水温度4 个特征变量作为空冷机组的稳态判定指标，滑动窗口具体参数见表4。经过工况筛选后，全年稳态工况数据量为103 730，在数据样本中随机抽取15%的数据作为测试集，用于模型性能检验，其余部分划分为训练集，用于模型的迭代和训练，数据划分如图2所示。

表4 滑动窗口具体参数Tab.4 Specific parameters of the sliding window

3 分析方法

3.1 BP神经网络

人工神经元是受自然神经元静息和动作电位产生机制的启发而建立的运算模型，使计算机能像人脑一样自发地学习并做出决策。BP 神经网络是1986 年由以Rumelhart 和McClelland 为首 的 科学家提出的概念，是一种按照误差逆向传播算法训练的多层前馈神经网络［11-12］。

图2 稳态工况数据划分Fig.2 Steady state data partition

典型的BP 神经网络结构如图3 所示。作为当前应用最广泛的神经网络，BP 神经网络由输入层、隐藏层和输出层组成，层与层直接连接，隐藏层节点的输出信号经激活函数传播到输出层［13］。BP 神经网络可以对任意复杂函数进行逼近，信号按照输入层到输出层的方向传递，而权值和偏置值的不断修正方向为信号传递的逆方向［14］。BP 神经网络具有很强的非线性映射能力、高度的自学习和自适应能力以及一定的容错能力，无需事先确定输入与输出之间映射关系的数学方程，并且在局部神经元受到破坏后，对全局的训练结果不会造成大的影响。本文所建立的BP神经网络模型具体参数见表5。

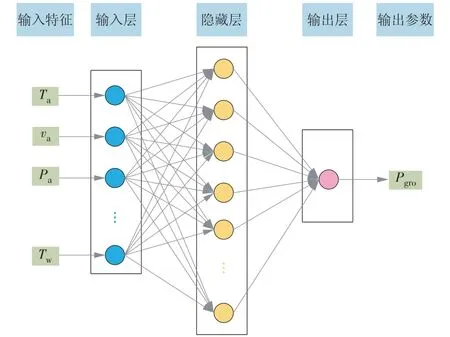
图3 典型的BP神经网络结构Fig.3 Configuration of a classical BP neural network

表5 BP神经网络模型具体参数Tab.5 Specific parameters of the BP neural network model

3.2 随机森林

集成学习（EL）包括多个单一的学习机，研究表明，集成学习机相对于单一学习机有更高的泛化能力和预测准确率［9］。作为一种新兴的、高度灵活的EL算法，随机森林（RF）算法拥有广泛的应用前景。

RF算法引入重采样技术Bagging 并随机选择分裂属性，其核心思想是并列生成多棵决策树组成森林，通过增加广度来防止过拟合，达到最优分类或回归，解释输入特征项x1，x2，x3，…，xn对标签项Y 的作用，使其泛化性能相较原学习器得到显著的提升［15-16］。图4 为随机森林预测模型的构建流程，其具体构建步骤如下［17-18］。

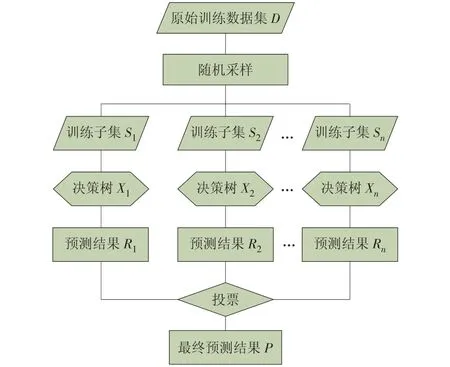
图4 随机森林预测模型构建流程Fig.4 Construction flow of a Random Forest forecasting model

（1）随机抽样训练决策树，利用Bootstrap 重采样法从初始样本集D 有放回地抽取m 个样本集，m个样本集生成n个训练子集（n＜m）。

（2）随机选取属性作为节点分裂属性，对n组训练子集分别构建决策树，每棵树的分裂节点仅随机选取样本的一部分属性来进行分裂，直至生长到指定的树的深度。

（3）按照步骤（2）重复操作，直到构建出n 棵回归决策树。

（4）模型的最终输出结果由子决策树的输出结果投票产生。

3.3 模型评价指标

本文采用绝对平均误差（δMAE）、相对平均误差（δMAPE）、均方根误差（δRMSE）及决定系数（R2）为模型评价指标，来评价模型预测结果的准确性与泛化性［19-20］。通常情况下，模型的δMAE，δMAPE和δRMSE越小，模型精度越高。决定系数的取值范围为［0，1］，其大小与回归模型性能成正比［21-23］。

均方根误差δRMSE

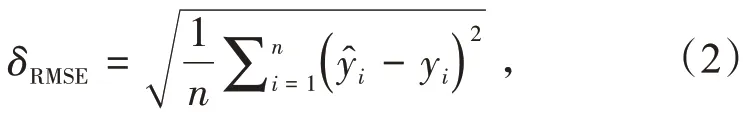
平均误差δMAE

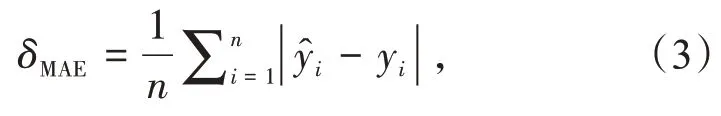
平均相对误差δMAPE

决定系数R2

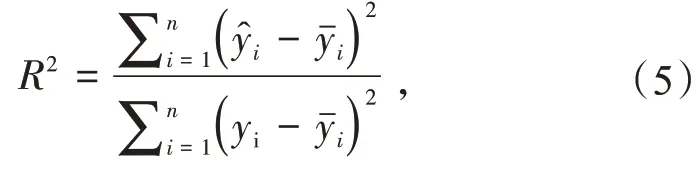
式中：n为测试样本数量；yi和yˆi分别第i个样本的真实值和预测值；yˉi为序列yi的平均值。

3.4 相关性分析

本文引入Pearson 相关系数［14，24］来分析输入特征与机组功率之间的关联程度，其计算公式为

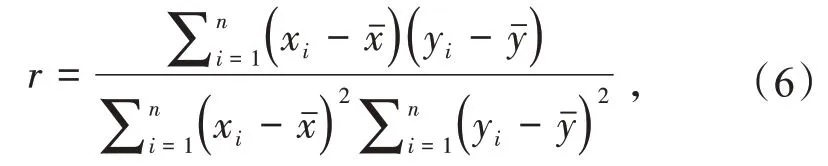
式中：xi，yi为特征参数序列的第i个数值；xˉ，yˉ为特征参数序列的平均值。

Pearson 相关系数的取值范围为［-1，1］，r＞0 表示x 和y 呈线性正相关，r＜0 表示x 和y 呈线性负相关。r的绝对值越大，x与y之间的相关性越强［14］：

（1）1.0≥|r|＞0.8时，特征间呈极强相关性；

（2）0.8≥|r|＞0.6时，特征间呈强相关性；

（3）0.6≥|r|＞0.4时，特征间呈相关性；

（4）0.4≥|r|＞0.2时，特征间呈弱相关性；

（5）0.2≥|r|≥0时，特征间呈极弱相关性［15］。

4 结果及分析

4.1 模型敏感性分析

基于Matlab 软件平台建立BP 神经网络算法和随机森林算法的案例机组负荷预测模型。对于BP神经网络模型，通过隐藏层神经元数目的变化，获得神经元数目对BP神经网络预测模型性能的影响，如图5 所示。对于随机森林模型，通过决策树数目的变化，获得决策树数目对随机森林预测模型性能的影响，如图6所示。

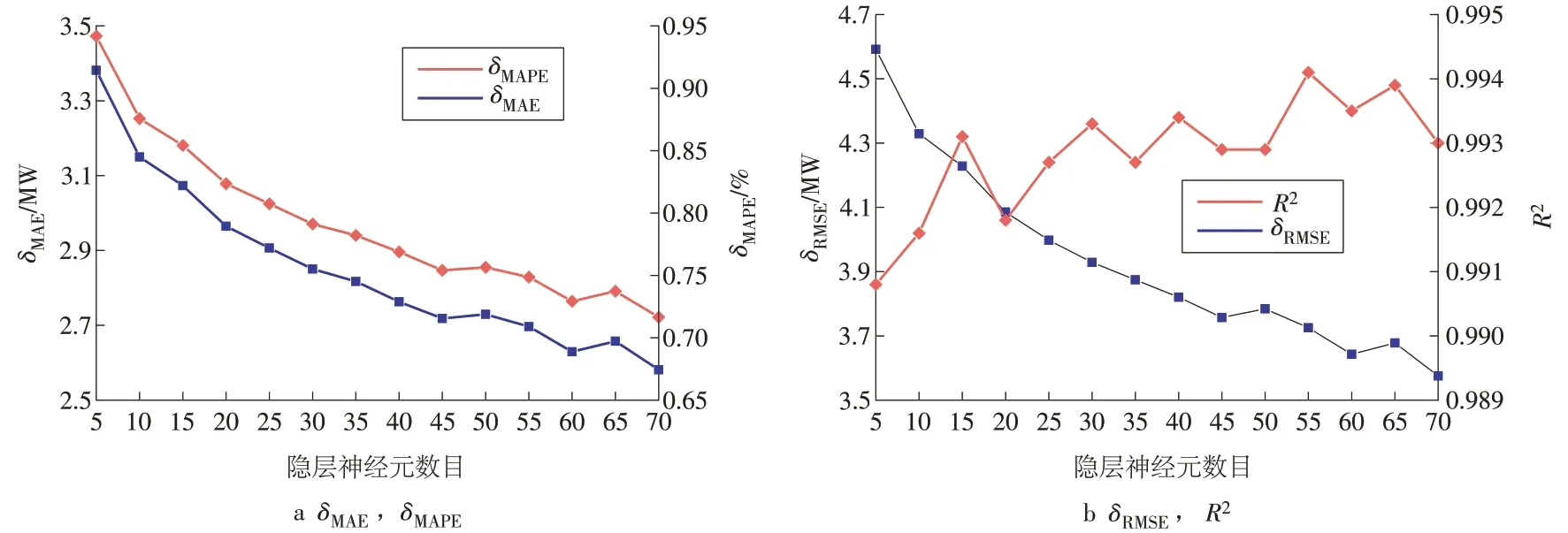
图5 隐层神经元数目对BP神经网络预测模型的影响Fig.5 Influence of the neurons number of hidden layers on the BP neural network prediction model

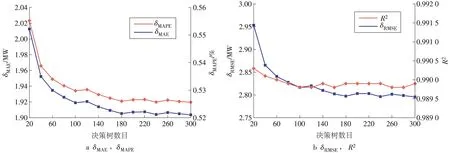
图6 决策树数目对随机森林预测模型的影响Fig.6 Influence of the number of decision trees on the Random Forest prediction model

4.2 预测结果对比分析

针对4.1 中BP 神经网络和随机森林模型的敏感性分析结果，本文选取隐层神经元数目为70，决策树数目为300，分别建立机组功率预测模型并对预测结果进行对比分析。结果表明，随机森林模型具有预测精度高、计算速度快等优点，预测结果数值对比见表6，图形对比如图7所示。

表6 BP神经网络与随机森林模型预测结果对比Tab.6 Prediction results made by BP neural network model and Random Forest prediction model

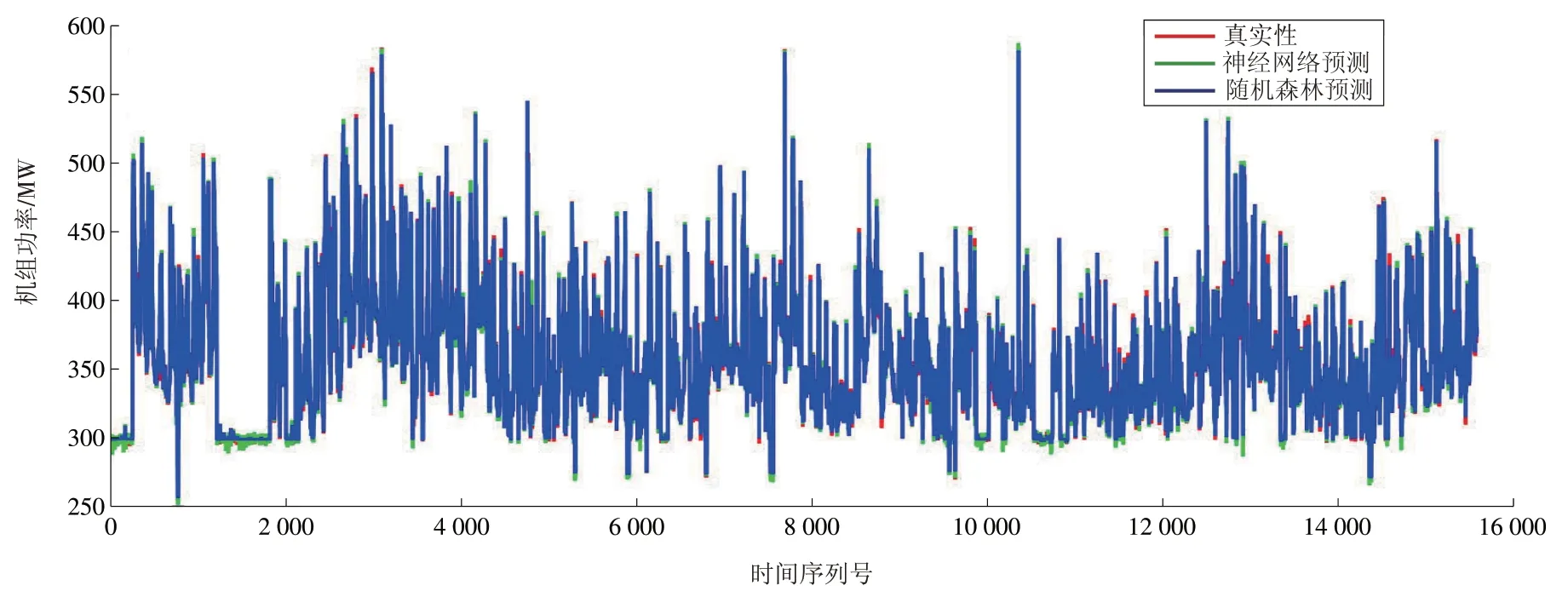
图7 BP神经网络模型与随机森林模型预测结果对比Fig.7 Comparison of results made by BP neural network model and Random Forest prediction model

4.3 模型输入特征优化

基于随机森林算法预测空冷机组负荷的诸多优点，考虑到机组在线状态检测对计算速度和准确性的较高要求，本文仅对随机森林模型进行优化分析。引入皮尔森相关系数对输入特征参数进行筛选，在保证模型预测精度基本不变的前提下，减少特征输入和数据维度，以简化模型结构，节省建模和预测时间［25-26］。各输入特征与机组功率之间的皮尔森相关系数如图8所示。

由图8 可见：主蒸汽流量、凝结水流量、主蒸汽压力与机组功率呈强相关性，其皮尔森相关系数分别为0.957 3，0.951 6，0.902 8；其次，由于凝汽器真空度对空冷机组整机效率有较大影响，因此凝汽器背压、凝结水温度和环境温度与机组功率有一定的相关性，而其他输入特征与机组功率相关性不大。考虑到空冷机组凝汽器背压变化频繁且幅度较大，本文选取环境温度、主蒸汽流量、主蒸汽压力、凝结水流量和凝结水温度5 项特征参数作为输入特征，建立部分因素的随机森林预测模型，并将预测结果与全因素随机森林预测模型的预测结果进行对比分析，数值对比见表7，图形对比如图9所示。

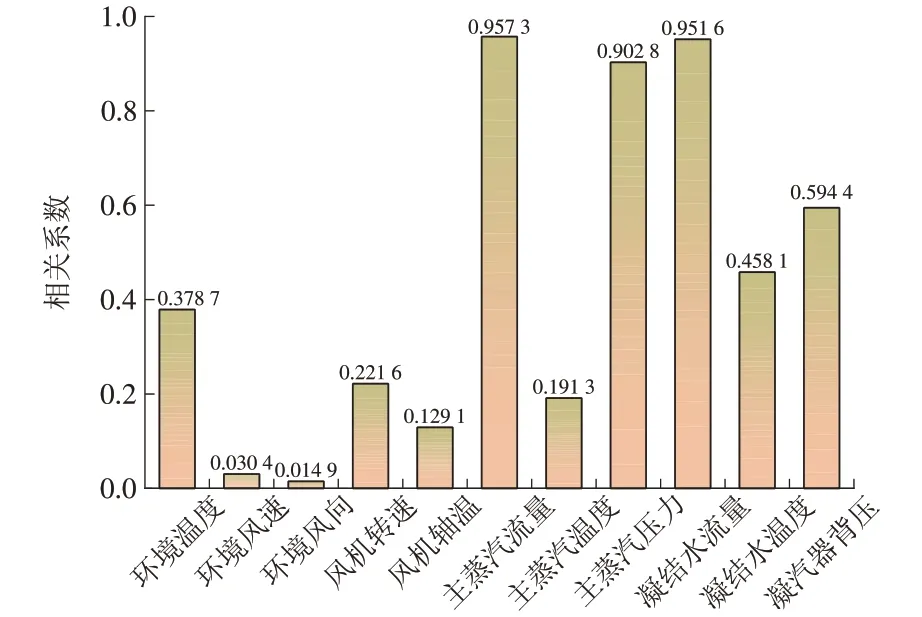
图8 各输入特征与机组功率的相关系数Fig.8 Correlation coefficients between various input characteristics and unit power

由表7可知：相比全因素随机森林预测模型，部分因素随机森林预测模型的预测精度虽然略有下降，但仍在可接受范围内；2 种模型的绝对误差（δMAE）差异仅为-0.355 3 MW，相对误差（δMAPE）差异仅为-0.097 1 百分点，部分因素随机森林预测模型的建模速度和预测速度均有较大提升。

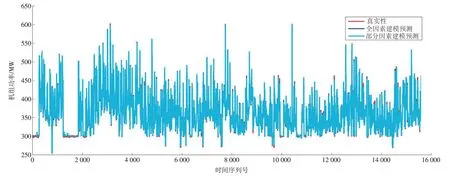
图9 随机森林全因素建模与部分因素建模预测结果对比Fig.9 Random Forest prediction results made by all factor modeling and partial factor modeling

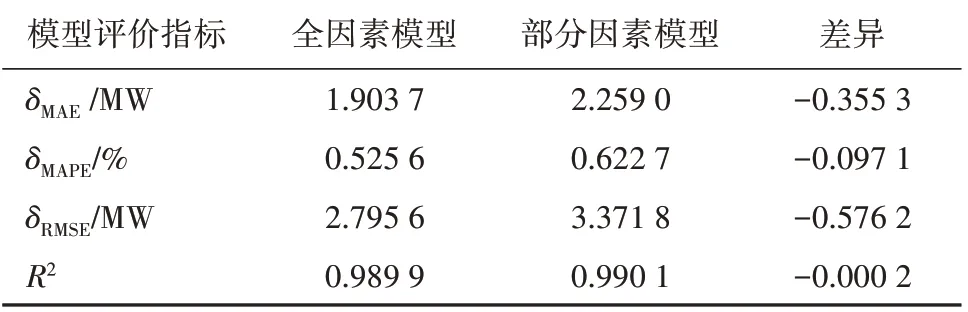
表7 随机森林全因素建模与部分因素建模预测结果对比Tab.7 Random Forest prediction results made by all factor modeling and partial factor modeling

4.4 分区建模模型优化

由于燃煤发电机组运行工况复杂多变，机组功率的变化范围较大，对模型预测结果的精确性存在一定影响。查阅案例机组的相关设计资料和实际运行数据，本文按机组负荷对机组稳态工况数据进行分区，利用不同负荷区间的运行数据建立不同负荷段的子模型，代替基于整体数据的预测模型，以提升预测精度。考虑到稳态工况数据点的分布，在保证每个负荷区间有充足数据量进行训练的前提下，按照机组热耗保证（THA）工况的75%，60%，50% ，将机组负荷划分为4 个区间并在各负荷区间建立相应的部分因素随机森林预测模型，计算结果见表8。

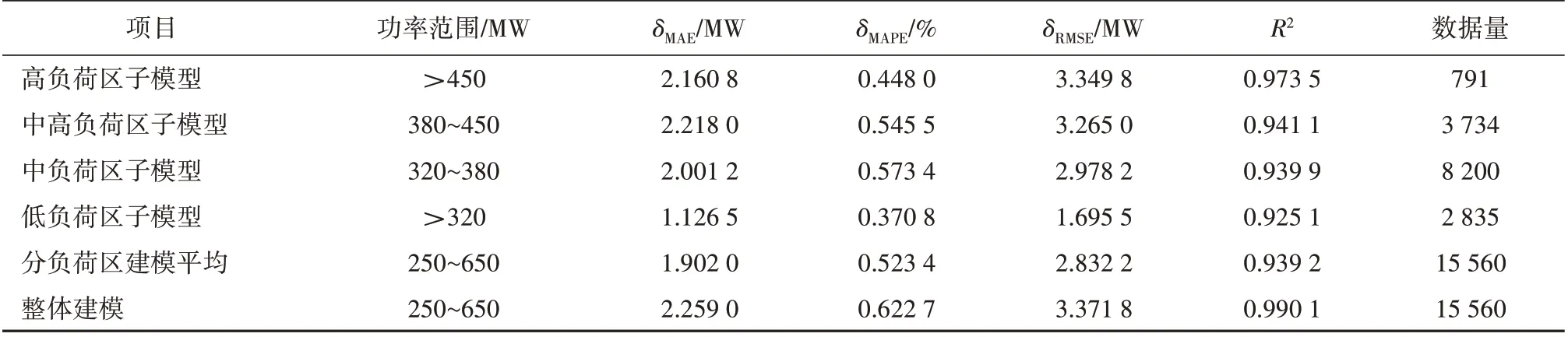
表8 随机森林分区建模与整体建模预测结果对比Tab.8 Random Forest prediction results made by partition modeling and overall modeling

由表8 可知：相比于不划分负荷工况区间的部分因素随机森林预测模型，各个负荷区内部分因素随机森林预测模型的预测精度均得到了提升；其中，低负荷区子模型的预测精度得到了显著提升，相比整体建模的预测结果，绝对平均误差（δMAE）下降 了11 325 MW，相对 平均 误 差（δMAPE）下 降 了0.251 9 百分点。分负荷区建模的部分因素随机森林预测模型绝对平均误差（δMAE）为1.902 MW，相对平均误差（δMAPE）为0.523 4%，证明该优化方法有效，模型预测结果的准确率得到了提升。

5 结论

本文基于某600 MW 空冷机组全年的运行数据，利用BP神经网络算法和随机森林算法对案例机组的功率进行预测。经过预处理数据和采用滑动窗口法筛选稳态工况，获得了建模所需的数据，分别建立了基于BP 神经网络和随机森林算法的预测模型，同时进行了敏感性分析。

结果表明，随机森林模型具有较高的预测精度和计算性能，其绝对平均误差（δMAE）为1.903 7 MW，相对平均误差（δMAPE）为0.525 6%。针对随机森林模型进行优化，通过皮尔森相关系数筛选模型输入特征，并根据机组功率划分负荷工况。对比分析优化前后的随机森林模型，在简化了模型输入特征参数的基础上，优化后的模型预测结果绝对平均误差（δMAE）降低了0.357 0 MW，相对平均误差（δMAPE）降低了0.099 3 百分点，表明优化效果显著，模型性能得到了进一步提升。