单抽供热机组负荷控制系统的解耦设计及动态响应特性研究

秦海山，栾丛超，侯晓宁，种道彤*

（1.华电郑州机械设计研究院有限公司，郑州450046；2.陕西省能源高效清洁转换工程技术研究中心，西安710049）

0 引言

目前，供热机组大多仍采用“以热定电”的运行方式，在热网负荷频繁波动时无法满足电网自动发电控制系统（AGC）的要求。在国家促进可再生能源并网发电，发展高效、灵活火电技术的政策背景下，供热机组控制系统优化需求日渐突出。

针对热电耦合现象，王漪等［1］利用能量平衡法计算出不同采暖抽汽流量与工业抽汽流量下机组发电量的取值范围，为电网调度提供参考。一些学者从供热系统优化角度出发解决热电耦合难题，如加入吸收式热泵、电锅炉、蓄热罐等［2-4］。

目前，控制系统解耦优化方面已经取得一定进展。达成莉［5］从控制器设计方面入手，详细剖析了自适应解耦、智能解耦等方法。李锋等［6］针对传统纯凝机组协调控制系统应用于供热机组效果不佳的问题，在所研究的110 MW 热电厂协调控制系统基础上加入被控量前馈差值信号，以改善热电耦合特性。朱建忠等［7］提出利用扩增状态观测器的方法设计超前环节与增益补偿，以改善锅炉制粉系统的动态特性从而实现解耦。邓拓宇等［8］从供热侧波动对发电功率和汽轮机机前压力的影响角度出发，设计相应解耦方案，改善供热机组供热侧负荷变动对机组发电功率的影响。

供热机组的热、电负荷调节系统不完善，协调控制系统的解耦设计作为可行的优化策略，对实现热电解耦和提高供热机组运行灵活性具有重要意义。本文以某330 MW 单抽供热机组为研究对象，在对供热机组的非线性动态模型进行小偏差线性化的基础上，采用相对增益法与对角矩阵解耦法进行协调控制系统解耦设计。当热负荷与电负荷发生变化时，分析解耦前后控制系统作用下供热机组的动态特性，为供热机组的运行提供指导。

1 供热机组数学模型的线性化

目前应用的单抽供热机组可选汽源有再热热段抽汽、再热冷段抽汽、中压缸内某一级抽汽以及中压缸排汽等。本文以中压缸排汽供热的330 MW单抽供热机组为例，在文献［9］提出的供热机组数学模型的基础上进行控制系统解耦设计。机组额定供热工况下的参数为：发电功率，235 MW；汽轮机前蒸汽压力，16.67 MPa；中压缸排汽压力，0.35 MPa；供热抽汽质量流量，400 t∕h。

为了方便控制系统设计，需要将微分方程进行拉普拉斯变换，并通过取增量方程的方法对其进行线性化。线性化后的传递函数［10-12］为

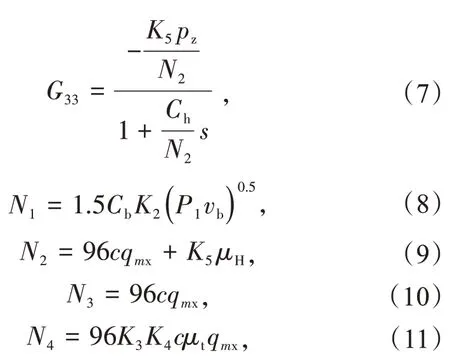
式中：Gij为传递函数；i 取1，2，3，分别代表给煤量、汽轮机调节阀开度、供热低压调节阀开度；j 取1，2，3，分别代表主蒸汽压力、机组发电功率、供热抽汽压力；vb为锅炉燃烧速率；pt为汽轮机机前压力；pz为供热抽汽压力；μt为汽轮机调节阀开度；μH为低压调节阀开度；qmx为热网循环水流量。

其他动静态参数可由运行数据拟合或系统辨识得到：tf为制粉惯性时间；Cb为锅炉蓄热系数；ti为汽轮机惯性时间；Ch为热网加热器蓄热系数；t 为制粉过程延迟时间；P1为额定发电工况下单位燃料量对应机组发电功率；K2为压差拟合系数；K3为汽轮机增益；K4为高中压缸做功占整个汽轮机做功的比例；K5为低压缸增益；c为热网循环水的有效比热容。

供热机组的主要被控量为发电功率、供热抽汽压力、汽轮机机前压力，主要输入量为燃料量、汽轮机主蒸汽调节阀开度、低压调节阀开度。因此供热机组为3 输入3 输出的多变量受控对象［13］，其传递函数矩阵为

式中：Pe为汽轮机发电功率；qmb为机组给煤量，t∕h；G13为供热调节阀开度对汽轮机机前压力的传递函数，G13=0。

2 基于静态相对增益的协调控制系统设计

2.1 基于静态相对增益的变量分析

传统的单元机组协调控制系统按照机炉协调方式主要分为2种：一种为汽轮机控制电功率、锅炉控制汽轮机机前压力的运行方式（以下简称炉跟机方式）；另一种为锅炉控制发电功率、汽轮机控制机前压力的运行方式（以下简称机跟炉方式）。大量学者对2 种协调控制系统进行了分析：炉跟机方式负荷响应更快，但汽轮机机前压力波动大；机跟炉方式机前压力平稳，但负荷适应性相对较差［14-18］。

以相对增益法确定机炉协调模式，可为进一步的解耦优化提供有利条件。相对增益表明输入量与输出量的关联程度，其值越接近1，关联程度越大。

首先采用相对增益矩阵法进行协调控制系统选型。假设一个多输入多输出系统的输入变量、输出变量个数均为n，其中一个输入变量为ci，一个输出变量为mj，根据相对增益的定义［19］，第1放大系数φij与第2放大系数Pij为

则相对增益λij为

通过推导，得到供热机组输入、输出变量间相对增益的计算公式，以λ11为例

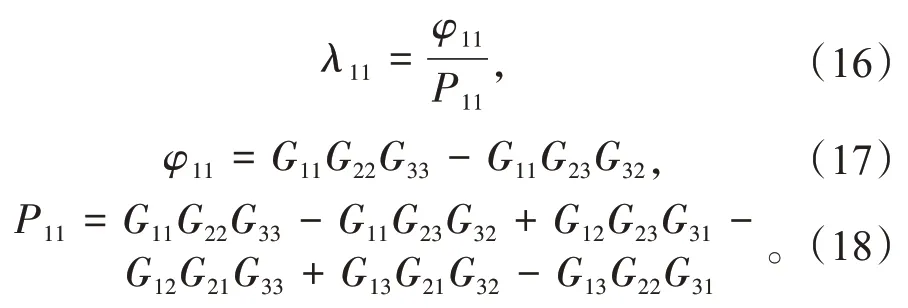
在复频域中，s=ωj，其中：s 为复频率；ω 为角频率；j为复数单位。工程应用范畴以静态相对增益作为依据即可，即ω=0。计算得到供热机组的全部9个静态相对增益［20］，见表1。

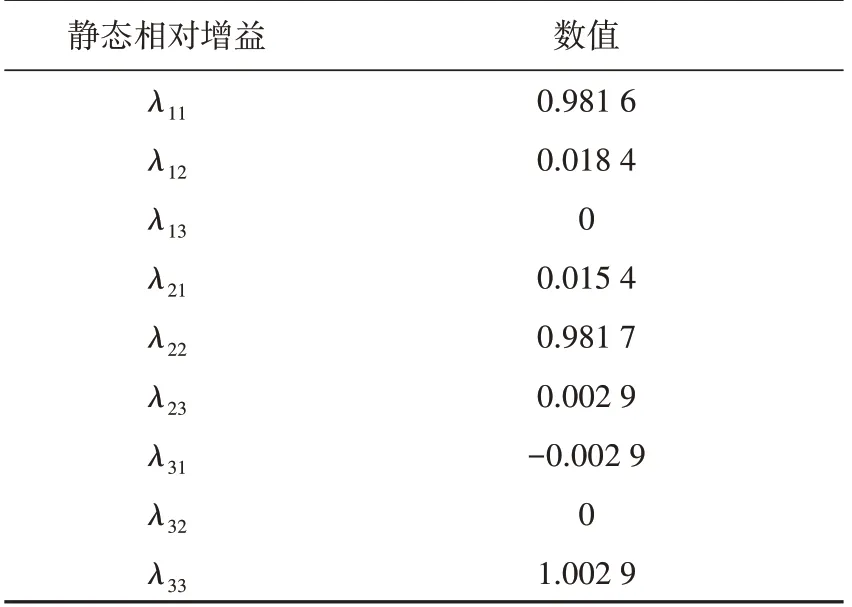
表1 各输入量对各输出量的静态相对增益Tab.1 Static relative gain of different input to each output

由表1可见：λ11，λ22，λ33接近1，说明给煤量控制汽轮机机前压力、汽轮机调节阀控制发电功率、低压调节阀控制供热抽汽流量能达到理想的控制效果；λ31为负，表明不能采用调节给煤量实现供热量的闭环控制。

2.2 控制系统分析与解耦设计

对于供热机组，如果仅采用给煤量控制汽轮机机前压力、汽轮机调节阀控制发电功率、低压调节阀控制供热抽汽压力3 个反馈回路的基本控制方案，在进行热、电负荷调节时会出现以下问题：当采用汽轮机调节阀控制发电功率时，供热抽汽流量出现波动；当利用低压调节阀调整供热抽汽流量时，发电功率发生变动［21-23］；同时，由于机炉耦合作用，热、电负荷在调整过程中都会引起机前压力的波动。

因此，对上文所确定的协调控制系统进行解耦优化设计是十分必要的。锅炉具有大延迟、大惯性的动态特性，因此给煤量的变化可给予汽轮机侧以及供热侧控制系统足够的反应时间，故为简化系统设计，锅炉侧不必设计解耦环节，汽轮机侧控制系统与供热侧控制系统增加解耦环节。图1为解耦设计优化后的控制系统结构，其中：G1，G2，G3为比例-积分-微分（PID）控制器；pt0为汽轮机机前压力给定值；P0为汽轮机发电功率给定值；pz0为供热抽汽压力给定值。

图1 解耦优化的供热机组协调控制系统结构Fig.1 Structure of the coordinated control system of a heating unit after decoupling optimization

D 为解耦环节，即为实现系统解耦增加的通道。D21，D23的设计原则为：使电功率负荷指令对汽轮机机前压力pt、供热抽汽压力pz的等效传递函数为0，即

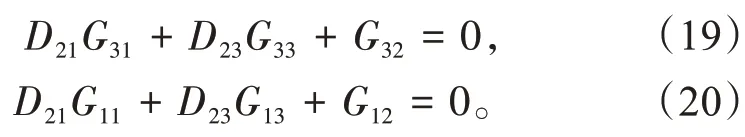
联立求解得到解耦环节的传递函数

D31，D32的解耦设计原则为：使低压调节阀开度μH对汽轮机机前压力pt、汽轮机发电功率Pe的等效传递函数为0，即

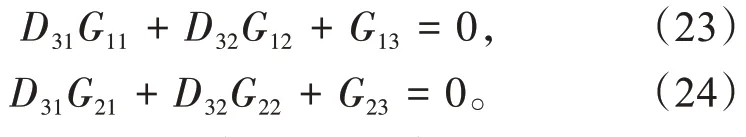
联立求解可得到解耦环节的传递函数

考虑到工程实现问题，可消除解耦器的不稳定项，实现静态近似解耦。解耦后的受控对象传递函数为

式中：W 为等效的受控对象传递函数，其中W12，W13，W23，W32为0；D为补偿环节的传递函数。

供汽负荷变化时，供汽压力给定值一方面经控制器G3、等效传递函数G23后对发电功率Pe施加影响，进而引发控制器G2改变输出值来调节汽轮机调节阀开度μt，而因G13为0，供汽压力给定值不会直接影响主蒸汽压力pt。解耦设计下，供汽压力给定值可通过3 条路径对发电功率Pe施加影响，且3 条路径的总和始终保持为0，削弱供汽负荷指令对发电功率的影响。

在解耦前的控制逻辑中，电功率给定值根据电网指令变化时，一方面经控制器G2、等效传递函数G12后对汽轮机进汽压力pt施加影响，进而引发控制器G1改变输出值来调节给煤量qmb；另一方面经控制器G2、等效传递函数G32后对供热抽汽压力pz产生影响。解耦设计下，电功率给定值可通过3 条路径减弱发电负荷指令对主蒸汽压力与供热抽汽压力的影响程度。

3 协调控制系统解耦前后供热机组动态特性

对给煤量控制汽轮机机前压力、汽轮机调节阀控制发电功率、低压调节阀控制供热抽汽压力的基本控制方案以及解耦设计方案进行仿真试验。其中，锅炉控制器、汽轮机控制器与供热控制器均采用比例积分（PI）控制器，完成参数整定后对工况进行模拟。机组初始运行工况下（发电功率为200 MW，供热抽汽流量为400 t∕h，汽轮机机前压力为16.67 MPa），为更加直观地展现供热负荷的变化，下文均给出供热抽汽流量的响应结果而非供热抽汽压力。

3.1 供热抽汽负荷阶跃变化时供热机组的动态特性

为对比控制系统优化前后供热抽汽负荷变化时机组的动态响应，在机组运行至20 000 s 时，供热抽汽流量需求值分别阶跃上升至500 t∕h、阶跃下降为300 t∕h，图2—4 为供热机组主要参数的动态响应曲线。

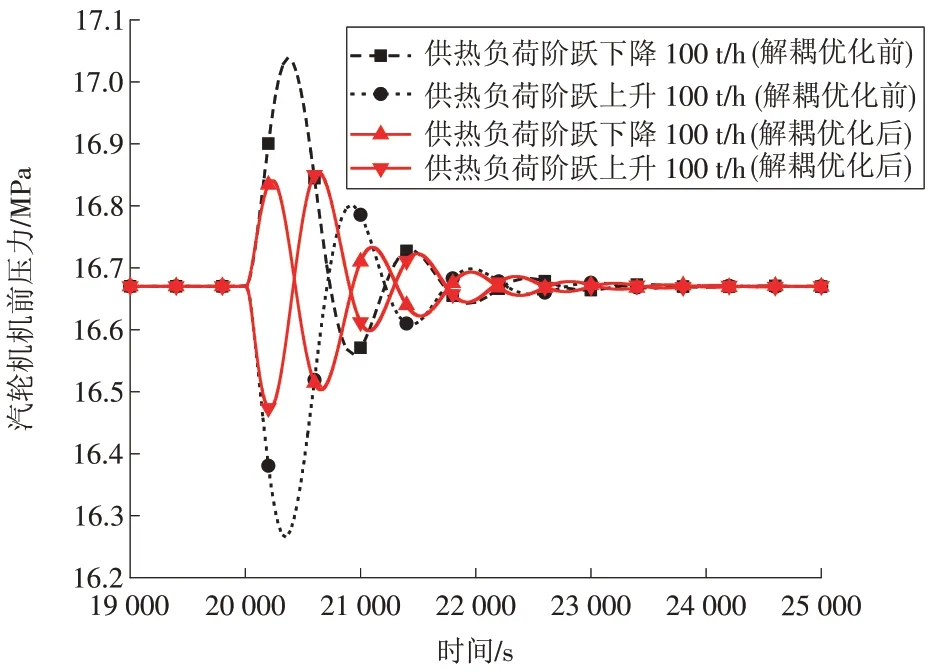
图2 供热抽汽流量阶跃变化时汽轮机机前压力动态特性Fig.2 Dynamic characteristics of the steam turbine front pressure under stepped change of extraction steam flow

图3 供热抽汽流量阶跃变化时机组电功率动态特性Fig.3 Dynamic characteristics of the power under stepped change of extraction steam flow

图4 供热抽汽流量阶跃变化时供热抽汽流量动态特性Fig.4 Dynamic characteristics of the extraction steam flow under stepped change of extraction steam flow

供热负荷的变化会引起主蒸汽压力和发电功率的扰动，主蒸汽压力稳定与否关系到机组能否安全稳定运行，而发电功率则要满足电网指令，不能出现长时间大范围的波动。当供热机组的热负荷阶跃上升时：若机组协调控制系统不进行解耦优化，机前压力最大波动为0.40 MPa，发电功率最大波动为10.25 MW；解耦优化后，机前压力最大波动为0.20 MPa，发电功率最大波动为3.61 MW。当供热机组的热负荷阶跃下降时：若机组协调控制系统不进行解耦优化，机前压力最大波动为0.37 MPa，发电功率最大波动为8.30 MW；解耦优化后，机前压力最大波动为0.17 MPa，发电功率最大波动为3.16 MW。

汽轮机惯性时间常数较小，因此，供热负荷变化时，供热抽汽流量能够实现快速准确的响应。解耦优化后的控制系统能够有效降低供汽流量阶跃变化带来的机组发电功率与主蒸汽压力扰动。解耦设计能够减弱供热低压调节阀开度对发电功率和主蒸汽压力的影响，使供热机组在供汽流量变化时能够保持系统的相对稳定，有利于供热供汽的进行。

3.2 不同供热抽汽负荷变化幅度对供热机组的影响

为研究不同供热抽汽负荷变化幅度下供热机组的响应特性，在机组以初始工况运行至20 000 s时，计算供热抽汽流量分别阶跃至425，450，500 t∕h时的机组主要参数响应曲线，如图5—7所示。

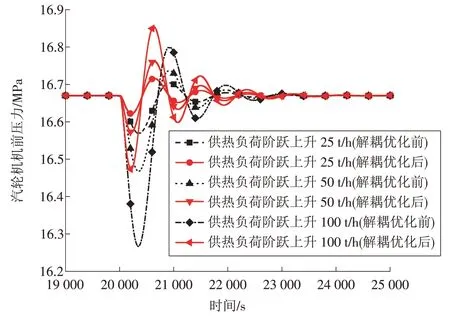
图5 不同供热抽汽负荷变化幅度下机组汽轮机机前压力动态特性Fig.5 Dynamic characteristics of the steam turbine front pressure varying with different-level fluctuation of extraction steam flow

不同供热抽汽负荷变化幅度指令下，供热抽汽流量都能够实现快速响应，但不同供热抽汽流量变化幅度下，供热机组的发电功率、主蒸汽压力扰动幅度不同：供热抽汽负荷阶跃幅度越大，发电功率、主蒸汽压力的最大扰动幅值越高，且发电功率、主蒸汽压力最大扰动幅值与供热抽汽流量变化幅度成正比。

图6 不同供热抽汽负荷变化幅度下机组电功率动态特性Fig.6 Dynamic characteristics of the power varying with different-level fluctuation of extraction steam flow

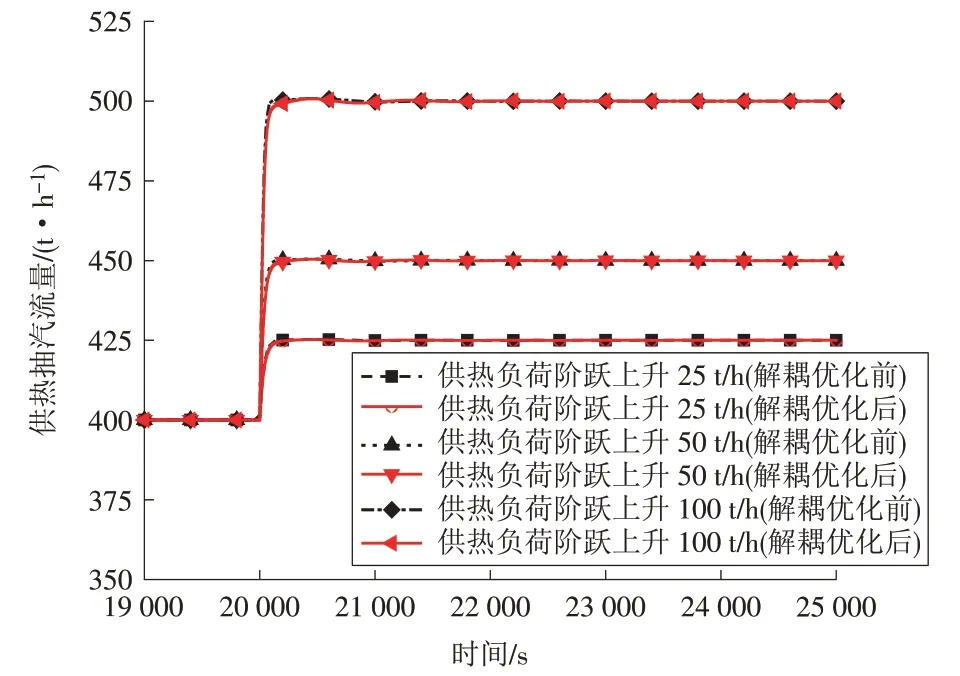
图7 不同供热抽汽负荷变化幅度下机组供热抽汽流量动态特性Fig.7 Dynamic characteristics of the extraction steam flow varying with different-level fluctuation of extraction steam flow

解耦优化前，供热抽汽流量变化幅度每增加10 t∕h，发电功率最大扰动幅值增加1.0 MW，主蒸汽压力最大扰动幅值增加0.040 MPa；解耦优化后，供热抽汽流量变化幅度每增加10 t∕h，发电功率最大扰动幅值增加0.4 MW，主蒸汽压力最大扰动幅值增加0.022 MPa：因此，供热负荷变化时，解耦优化后的系统更加可靠。

3.3 不同电负荷变化速率下供热机组的动态响应

在电负荷变化过程中，供热机组因汽轮机进汽量变化而导致供热抽汽流量也发生改变，因此，不同电负荷变化速率下供热机组的动态响应值得进一步研究。当机组运行至20 000 s 时，供热机组发电功率分别以1.5，3.0，4.5 MW∕min 的速率升至260 MW 和降至140 MW，图8—10 为供热机组相应的动态响应曲线。

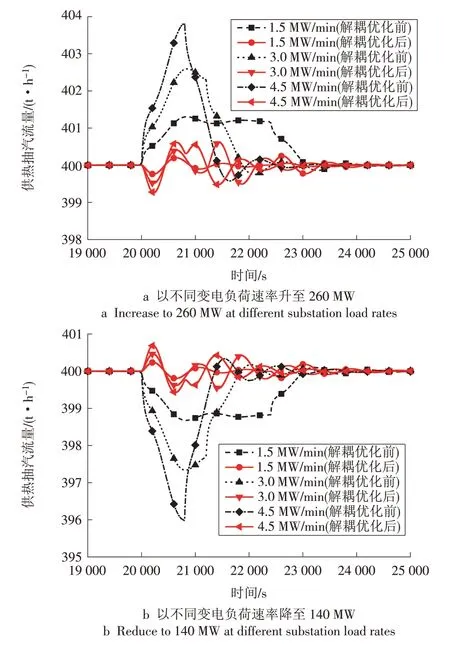
图8 不同电负荷变化速率下机组供热抽汽流量动态特性Fig.8 Dynamic characteristics of the extraction steam flow at different variation rates of electric load

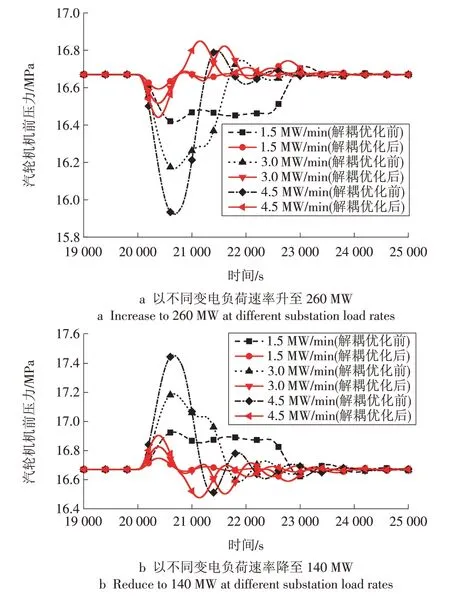
图9 不同电负荷变化速率下机组汽轮机机前压力动态特性Fig.9 Dynamic characteristics of steam turbine front pressure at different variation rates of electric load

图10 不同电负荷变化速率下机组电功率动态特性Fig.10 Dynamic characteristics of the unit power at different variation rates of electric load

在电负荷变化过程中，电功率超调量随着电负荷变化速率的提高而增加，解耦优化后的控制系统在较高的电负荷变化速率下有效改善了控制品质，使发电功率超调量更小。不同电负荷变化速率引起的供热抽汽流量与主蒸汽压力扰动幅度不同，电负荷变化速率越快，扰动的幅度越大。解耦优化后升负荷过程中，电负荷变化速率每增加0.5%，汽轮机机前压力最大变化幅度增加约0.06 MPa，供热抽汽流量最大扰动幅度增加约0.20 t∕h。

解耦优化前，4.5 MW∕min电负荷变化速率下主蒸汽压力最大变化幅度为0.74 MPa，供热抽汽流量最大变化幅度为3.85 t∕h；解耦优化后，4.5 MW∕min电负荷变化速率下主蒸汽压力最大变化幅度为0.23 MPa，供热抽汽流量最大变化幅度为0.83 t∕h。解耦设计能够提高供热机组电负荷变化时的负荷响应速度，同时可以有效降低供热抽汽流量扰动与主蒸汽压力扰动，有利于供热机组热负荷的供应以及机组的安全运行。

此外，电负荷变化速率较高（如4.5 MW∕min）时，解耦优化后的系统在机组电负荷开始变化2 000 s 后对供热量、主蒸汽压力的影响基本消除，此时可以认为耦合解除；而解耦优化前系统供热量、主蒸汽压力波动要持续到3 000 s 左右，给机组带来持续影响，不利于变负荷运行。

4 结论

本文将单抽供热机组非线性数学模型线性化，计算得到供热机组相对增益，并以此为参考完成供热机组控制的变量配对。应用动态解耦理论对供热机组汽轮机侧、供热侧进行解耦设计，分析解耦前后控制系统作用下的供热机组负荷调节的动态特性。研究结果可为多抽供热机组、高背压供热机组、切缸改造供热机组的设计提供一定的参考，但需进一步论证。本文主要得出以下结论。

供热机组可采用相对增益法确定变量配对方式：调节阀控制发电功率、给煤量控制汽轮机机前压力、低压调节阀控制供热抽汽压力。基于对角解耦理论，在汽轮机侧与供热侧控制系统分别增加2个解耦器的设计能够有效降低电负荷变化过程中供热抽汽流量、汽轮机机前压力的波动；同时，热负荷变化过程中供热机组的发电功率、汽轮机机前压力扰动得到有效控制。

在供热负荷调节过程中，随着供热负荷变化幅度的增大，供热机组发电功率以及汽轮机机前压力的扰动幅度逐渐增大。解耦优化后，供热抽汽流量变化幅度每增加10 t∕h，发电功率最大扰动幅值增加约0.4 MW，主蒸汽压力最大扰动幅值增加约0.022 MPa。而在电负荷变化过程中，供热抽汽流量与汽轮机机前压力同样存在扰动并与电负荷变化速率成正比。解耦优化后升负荷过程中，电负荷变化速率每增加0.5%，汽轮机机前压力最大变化幅度增加约0.060 MPa，供热抽汽流量最大扰动幅度增加约0.2 t∕h。