基于里德堡原子EIT的微波电场感知

梁 敏，孟宪川，王 静，林丽丹，彭延东

(1.山东科技大学 电气与自动化工程学院，山东 青岛 266590；2.山东科技大学 电子信息工程学院，山东 青岛 266590；3.潍坊中电万潍热电有限公司，山东 潍坊 261000)

近年来，随着微波精密测量广泛应用于微波光通信、遥感、医疗和国防等领域，基于原子相干的微波电场感知与成像引起研究者的极大兴趣[1]。当前微波电场精密测量大多基于电磁诱导透明效应(electromagnetically induced transparency，EIT)，即待测微波电场强度与EIT透射峰频率分裂大小成正比，通过光谱探测可以测量微波电场强度。

图1 基于里德堡原子的微波电场测量能级图与实验装置图[3]

(1)

(2)

式中，λp、λc分别是探测光和控制光波长。实验上可以准确测量拉比频率Ωm，由此可得微波电场强度E。这种利用里德堡原子测量微波电场的方法，具有探测精度高、自校准、连续测量、无探头干扰和小型化等优点[4]。

当前，微波电场测量主要研究方向之一是提高测量精度。2015年，Fan等[5]研究发现，通过优化原子气室结构，可以大幅提高测量精度；2016年，NIST研究小组利用频率失谐的方法提高微波电场探测的灵敏度[6]；Facon等[7]用薛定谔猫态研究了量子极限测量精度等。

近年来，课题组在基于里德堡原子EIT的微波电场感知方面做了一些创新工作。主要包括：提出了腔内EIT效应增强的微波电场测量方案，提高了系统的探测灵敏度和鲁棒性；进一步提高探测灵敏度和测量精度，改进了基于双EIT效应的强度和频率感知微波电场的方案；分析了双EIT系统色散特性，设计了利用相位检测方法感知微波电场信号的方案，系统信噪比和探测灵敏度大大提高；提出了利用EIT系统暗态间相互作用提高微波电场探测精度的非线性测量方案，暗态相互作用压窄EIT光谱线宽，最小可探测场强提高了一个数量级以上，并用缀饰态理论解释了光谱变化特性。

1 腔增强的微波电场测量方案

(3)

(4)

进一步得到介质的透射谱和腔透射谱的表达式分别为：

(5)

(6)

介质极化率χ的实部导致色散和附加的相移，χ的虚部引入吸收，导致场放大的衰减。

对比图2(a)和2(b)中不同微波电场强度下的腔内透射光谱T(ω)和介质透射光谱S(ω)，发现在微波场作用下T(ω)和S(ω)都呈现两个透射峰，而且腔透射谱峰-峰频率间距随微波场强线性变化，可以用来测量微波电场强度。关注系统的探测灵敏度，这与光谱分辨率即谱线宽度有关。数值结果表明，由于腔耦合，腔透射谱的线宽比介质透射谱的线宽大大缩小，能够提高光谱探测灵敏度。在相同条件下，腔透射峰的谱线半峰全宽约是2π×0.036 MHz，而介质透射峰的半峰全宽约是2π×0.81 MHz，可见腔耦合效应可以使探测灵敏度提高20倍以上。同时还研究了控制场强度对透射谱线宽的影响，发现当控制场减小时，透射谱线宽变窄，进一步提高了探测灵敏度。

对弱微波电场测量而言，一个重要测量指标是可探测的最小场强，由公式(1)可以看出微波电场可探测的最小场强取决于最小可分辨的EIT光谱。图3对比了有无腔耦合作用时最小可探测的EIT光谱，图3(a)是介质透射光谱，图3(b)是腔透射光谱，可以看出腔耦合有助于探测到更小的微波电场。数值模拟结果显示，基于腔透射谱的最小频率分裂间距Δf大约是2π×0.004 8 MHz，而未使用腔耦合的原子系统的最小频率分裂间距大约是2π×0.036 MHz，这说明腔增强的微波探测系统可探测的最小微波场强约为没有腔耦合时的1/8。

研究了频率失谐时透射谱线的变化情况，发现采用的腔增强方案具有较强的可调谐性和较宽的探测范围。虽然腔失谐会造成腔透射谱发生红移或蓝移，但是中心峰的频率分裂间距基本保持不变，说明该测量方案具有较强鲁棒性。

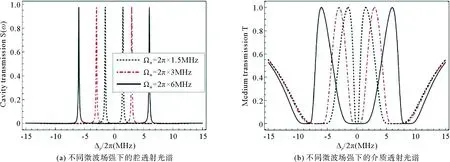
图2 腔透射光谱和介质透射光谱比较[8]

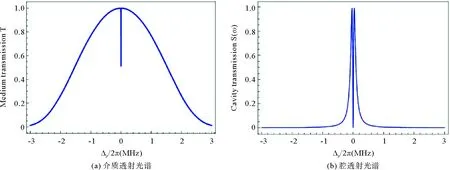
图3 有无腔耦合作用时最小可探测的EIT光谱[8]

2 双EIT系统光谱强度和频率感知微波电场方案

以前的微波电场测量大多数基于单暗态的EIT效应，未见到研究双暗态EIT效应对微波测量的影响。课题组提出了一种用双EIT系统光谱强度和频率感知微波电场的方案[9]。在级联型单EIT系统基础上，增加一个辅助跃迁，即用另一控制光耦合基态塞曼子能级与亚稳态跃迁，形成倒Y型的五能级双EIT系统。与前一部分相似，采用密度矩阵方法可以得到稳态时介质的极化率，进而得到介质透射光谱。研究发现：没有辅助跃迁时，四能级系统的光谱结构与前面一致；考虑辅助跃迁后，透射谱呈现三峰结构，原EIT窗口中出现电磁诱导吸收峰(electromagnetically induced absorption，EIA)；当微波场作用后，EIA峰发生分裂，形成两个窄的EIA峰。这源于辅助跃迁对原EIT系统的微扰作用。

有意思的是EIA峰的频率分裂间距随微波场强线性变化，可以用于测量微波电场强度。而且当探测场与驱动辅助跃迁的控制场同向传播时，发现光谱的多普勒频移明显，虽然原子EIA光谱产生红移和蓝移，但是频移后的吸收谱在两个频率位置处发生干涉相长，大大增强了EIA谱强度。特别是当微波场比较弱时，传统的EIT方案中，透射峰重叠不利于读出弱微波信号强度，如图4(a)所示；而多普勒效应增强的EIA谱峰值强度随微波信号线性变化，可以用于测量弱微波电场强度，如图4(b)所示。数值结果显示：不考虑多普勒效应时EIA光谱的峰值由Ωm=0.01Γ时的3×10-3MHz增强到Ωm=0.1Γ时的5×10-3MHz；多普勒平均后，EIA峰值由Ωm=0.01Γ时的0.05 MHz变化到Ωm=0.1Γ时的0.075 MHz，所以可以用EIA光谱强度测量弱微波信号电场分量。

图4 弱微波电场的频率和强度读出[9]

进一步研究以上基于EIA频率和强度的线性测量关系。图5(b)表示相对较强微波电场的EIA峰值和微波电场强度之间的线性关系；图5(c)和5(d)表示弱微波电场中无多普勒效应和有多普勒效应时EIA峰值与微波电场强度之间关系。从图5中可以看出，对较强的微波电场而言，EIA光谱的中心峰-峰频率间距Δf与微波电场强度成线性关系，即探测灵敏度与斜率成正比。数值模拟计算表明，单暗态时的曲线斜率约为0.23，而双暗态时的曲线斜率约为2.4，即双暗态系统的探测灵敏度比单暗态系统提高近7倍。当考虑多普勒效应时，强EIA光谱的峰值与微波电场强度成线性关系，这种强度读出方法将探测灵敏度提高了大约10倍。对弱微波电场测量而言，强度读出方法比频率读出方法表现出更高的探测灵敏度。

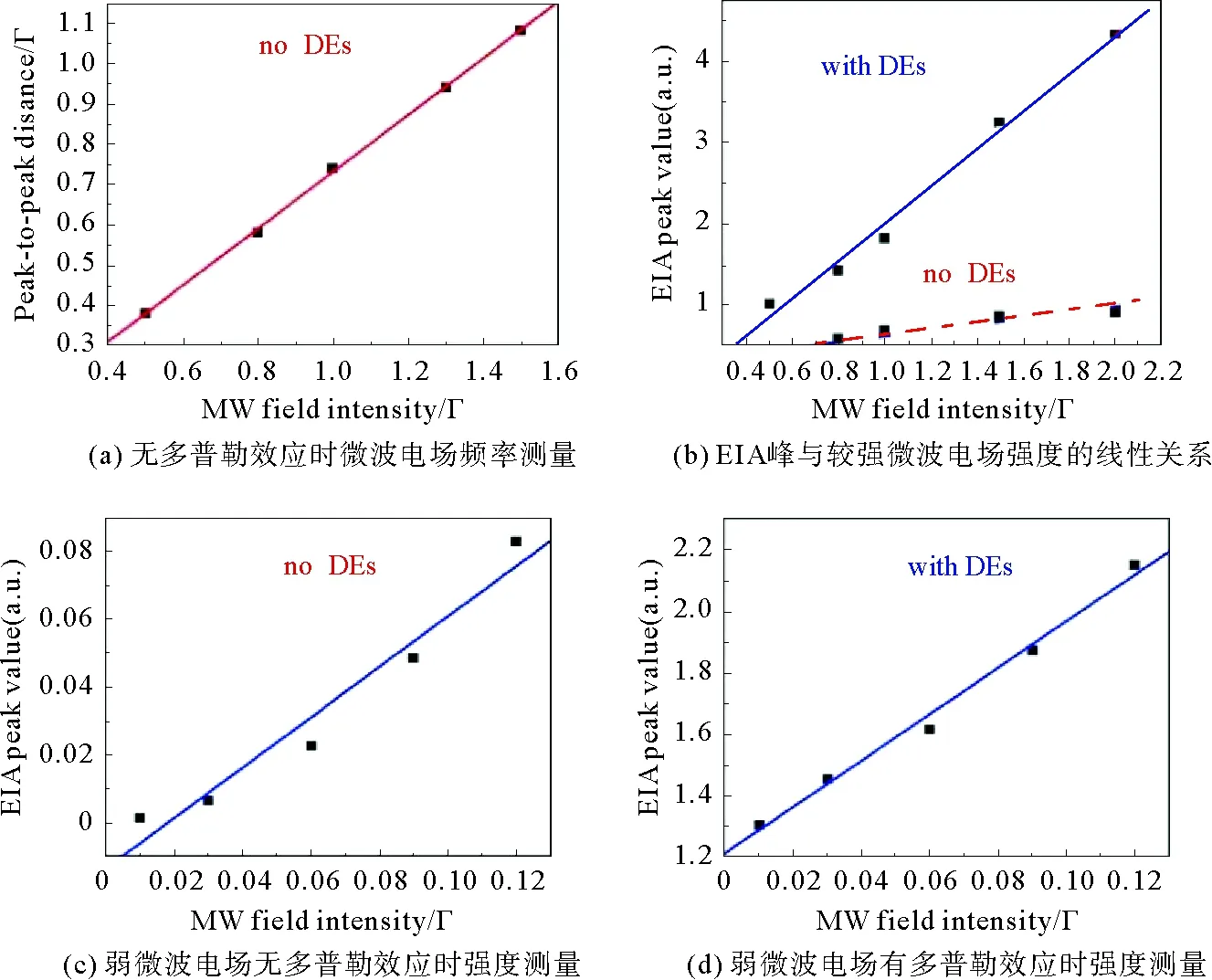
图5 微波电场中频率与强度读出[9]

3 双EIT系统色散测量微波电场方案

以前大多数测量微波电场的方法利用EIT透射光谱，即利用EIT透射谱峰-峰频率间距反映微波场强度变化。进一步的研究发现色散对透射脉冲影响很大，2015年，Fan等[10]实验证实了可以利用三棱镜的气室色散测量微波电场强度。棱镜型气室原子介质EIT窗口处的色散特性，使得透射光束在空间偏转。不同微波场引起EIT窗口处的色散不同，得到的透射光偏转角度不同，于是光谱角色散就可以显示出微波电场的微小变化。色散读出法在研究里德堡原子引起的色散非线性[11]以及利用频域干涉测量技术测量探测光束的振幅和相移[12-13]等方面都有较好的应用，且该方法具有高信噪比的特点，已经广泛地应用于非线性相移、电子态和光子相关等测量中。

本研究提出一种利用双EIT增强的色散[14]测量微波电场的方案。五能级里德堡原子属于双EIT系统，两个暗态之间的干涉效应会显著提高EIT窗口处的色散，而大的色散会引起透射脉冲的相移变大，这样通过光谱相位检验方法就可以读出微波场强的大小。色散方案基于相位探测，表现出较高的测量灵敏性。

首先，分析室温下原子多普勒效应引起的色散谱频移，色散曲线出现蓝移或红移，但是所有的曲线都在中心频率处表现出正常色散，故此处发生相长干涉，色散大幅增强。图6比较了有多普勒效应和无多普勒效应时的色散情况。从图6(a)中可以看出无多普勒效应时，介质极化率在共振频率处变化缓慢(见图6(a)中虚线)，色散比较小，约为0.001。在多普勒平均后，介质极化率的实部变得陡峭(见图6(a)中实线)，色散增加到0.015，振幅大约是不考虑多普勒效应时的10倍。

其次，分析微波场强对介质色散的影响，进而影响探测脉冲的相移。探测光场通过介质后，引起的相移Φ与n(ω/c)L成正比，即Φ～n(ω/c)L～kLRe[χ]/2，其中，n是介质折射率，ω是入射波长，c是光速，L是介质长度。根据文献[15]中介质极化率χ和介质折射率n的关系，进一步得到相移表达式为:

Φ～NRe[χ]L，

(7)

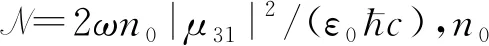
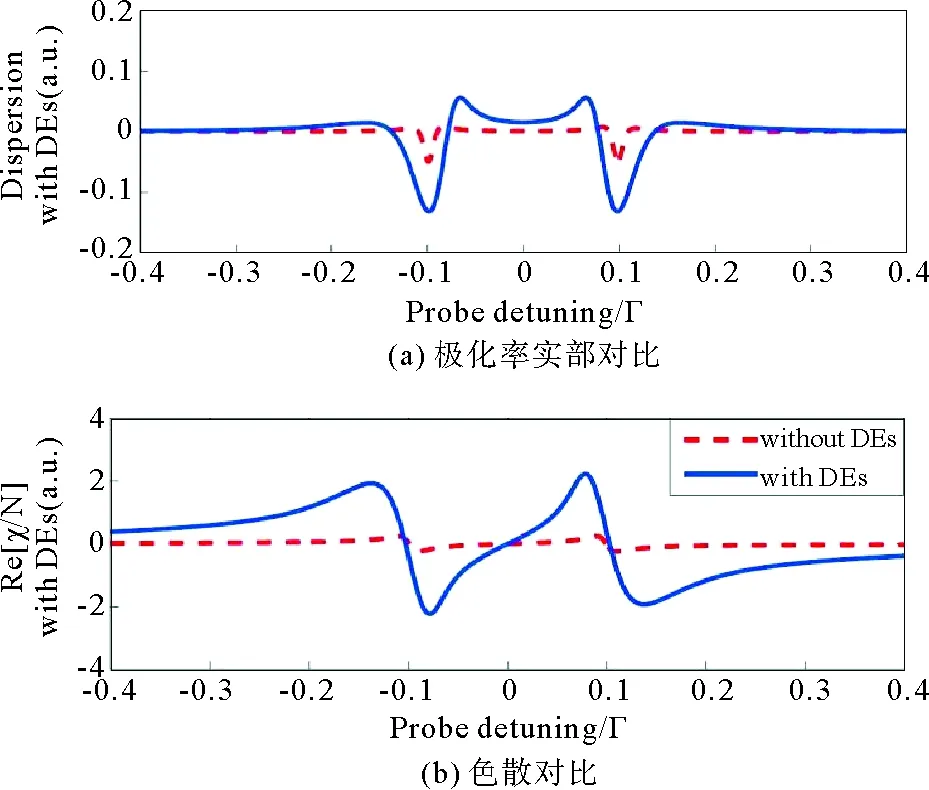
图6 有无多普勒效应时磁化系数实部和色散对比[14]

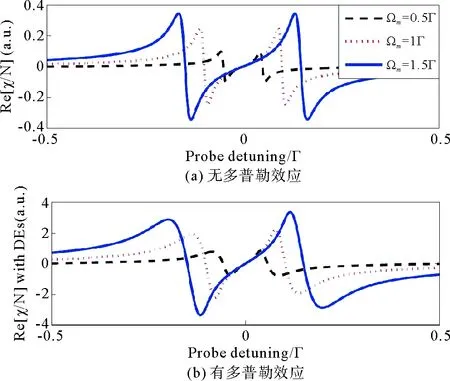
图7 不同微波场强下色散变化[14]

4 基于EIT的微波电场非线性测量方案

传统的里德堡原子测量微波电场的研究通常是在单暗态系统中进行，且一般在线性范围内讨论，本课题组提出了基于里德堡原子双EIT的非线性测量微波电场方案[16]。如图8所示，采用五能级系统，通过引入辅助基态跃迁，形成双EIT系统，进而导致系统暗态分裂形成双暗态系统。两个EIT子系统之间的干涉会导致较大的非线性吸收，非线性吸收谱的峰-峰频率间距Δf与微波电场强度成线性关系，可以用来感知微波电场强度。非线性吸收谱呈四峰结构，重点讨论两个中心峰。图9对比了线性吸收谱和非线性吸收谱的情况。发现：与线性吸收谱相比，非线性吸收谱的峰值增加了约两个数量级，而且谱线宽度大大缩小，比线性吸收谱的线宽大约窄了一个数量级。大峰值、窄线宽的吸收谱更适于实验中测量微波信号。同时,发现改变两个控制场的大小比值，会改变线性吸收谱和非线性吸收谱的峰-峰间距，当增加Ωc1/Ωc2时，两个中心峰的峰-峰频率间距变宽。由于峰-峰频率间距决定了最小可探测微波电场，所以当增加两个耦合场的比率时，可探测的最小微波电场变小。这样通过调节两个控制场的强度比值，可以调节最小可探测微波场强。

图8 里德堡原子五能级双暗态系统[16]

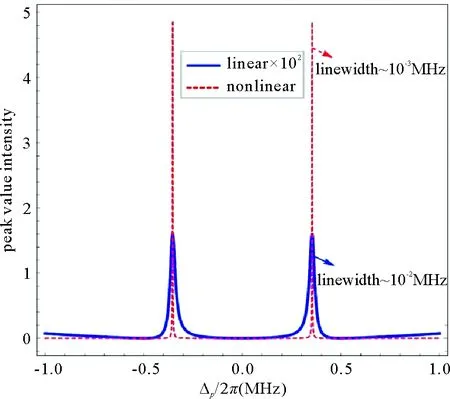
图9 相同参数下线性吸收谱与非线性吸收谱对比[16]

借助缀饰态理论[17]很好地解释了上述结果的物理机制。如图8(b)表示双暗态系统的缀饰态结构，在两个控制场(ωc1，ωc2)和微波电场(ωm)的耦合下，系统产生了四个新的本征态：

(8)

5 结论

本研究分析了里德堡原子微波电场计的测量原理，介绍了课题组近年的研究结果，从基于腔内单EIT方案到双EIT的测量方案，发现双EIT强度和频率测量可以适用于不同强度微波场测量；从基于EIT透射谱的测量到色散测量方案，发现色散法测量可以大幅提高信噪比；从以前基于EIT线性透射谱测量到基于双EIT的非线性测量，发现双EIT在压窄线宽上的明显优势。通过研究工作的整理和对比发现了提高微波电场测量精度的一些规律，用腔增强、暗态相互作用、高信噪比色散测量和超窄非线性光谱等方法丰富和发展了微波测量方案。研究工作对后续设计新型微波检测器件提供了更多参考。