一种相变储能电锅炉的蓄放热温度控制方法

张 来，李盛伟，梁海深

(国网天津市电力公司经济技术研究院，天津 300171)

目前，我国电网普遍存在负荷率低、峰谷差大[1-2]的问题，电力供应存在时段紧张。为解决取暖用热问题，推行电锅炉蓄热采暖技术，是实现电力“削峰填谷”、提高电网综合运行效益行之有效的方式[3]。

对于传统的燃煤锅炉、水蓄热式电锅炉，国内学者采用串级控制系统控制其主汽温。马莉等[4]采用PID串级控制系统控制电站燃煤锅炉主汽温，对主副调节器进行参数整定，仿真结果表明串级PID控制系统各项性能良好。胡文斌等[5]基于内模控制原理，针对过热汽温的串级控制系统给出了基于内模原理的PID控制器设计方法，该方法设计的PID控制器参数只有一个滤波器时间常数需要调整，方法简单方便。叶向前等[6]在常规PID主蒸汽温度串级控制系统的主回路中加入动态矩阵预测控制器(dynamic matrix predictive control, DMC)构成DMC-PID主蒸汽温度串级控制系统。可见串级控制系统控制电锅炉主汽温可以有效克服系统时变、非线性和大滞后的问题[7-8]。

在“煤改电”采暖中，传统电蓄热模式为水蓄热式电锅炉，其蓄放热方式多为“水-水”热交换，其时变、非线性特性小，易于控制。而相变储能电锅炉蓄热介质为固体相变材料，其蓄放热过程伴随着“热熔丝-空气”“固体相变材料-空气”、“空气-水”等热交换过程进行，加剧了相变储能电锅炉系统的滞后性、时变性和非线性，进而加大了对其出水温度的控制难度。目前关于相变储能电锅炉的温度控制方面的文献仍是空白。因此，本研究提出了一种新型的基于串级PID的相变储能电锅炉温度控制的方法，其中串级控制较单回路控制增加了一个包含二次扰动的副回路，提升系统的动态性能和抗扰动能力，使锅炉温度得到更稳定的控制，并且提高了生产过程中的安全性[9]。

1 相变储能电锅炉结构

相变储能电锅炉由电加热模块、储能材料模块、循环风机、调节阀、换热器、绝热隔板和保温层组成。电加热模块用于加热相变储能材料；储能材料模块由固体耐火砖[10]形式的相变储能材料[11-12]堆砌而成，固体砖内部有通透的孔道，利用空气流动进行热量交换；电加热模块和相变储能材料交替放置，实现更高效的热量交换；循环风机将空气循环，实现电锅炉不同模块之间的热量交换；调节阀控制循环空气流量，实现对电锅炉出水温度升高和降低的控制；换热器用于电锅炉内高温空气与电锅炉外热水进行热量交换，实现相变储能电锅炉供暖；绝热隔板将相变储能材料与循环空气风道隔离，实现锅炉温度控制；保温层用于保持相变储能电锅炉的内部温度，减小热量损失。电锅炉结构示意图如图1所示。

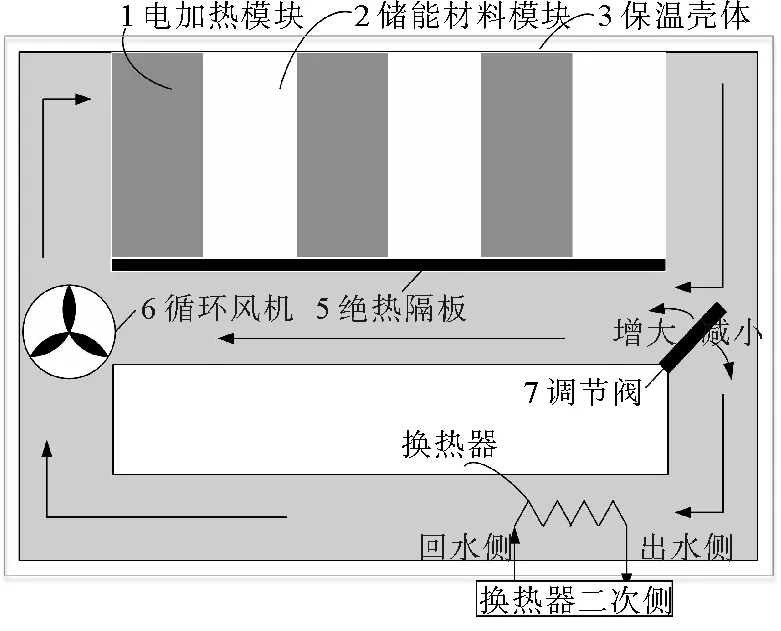
图1 相变储能电锅炉结构示意图

相变储能电锅炉采用间接换热的方式，安全性能较高，设备寿命较长，但初期成本较高[13]。纯放热阶段，循环空气将储能材料中的热量循环至换热器处进行热量交换；谷电蓄能阶段，电锅炉边蓄能边供暖，电加热模块将电能转化为热能，加热相变储能材料，循环空气将电加热模块以及相变储能材料中的热量一起循环至换热器处进行热量交换，实现相变储能电锅炉供暖。

2 相变储能电锅炉控制系统

2.1 单回路控制系统

单回路控制系统由调节器、执行器、被控对象和测量变送器组成。系统给定值为定值，在本系统中为电锅炉的目标出水温度。单回路控制系统实质上为一单闭环回路，系统进行负反馈调节，将输出值不断返回与设定值进行比较，直至被控制量达到设定值。单回路控制系统具有结构简单、调试方便的优点，单回路控制系统原理图如图2所示。

图2 单回路控制系统原理图

2.2 串级控制系统

串级控制系统是由多个调节器控制一个或多个执行器完成定值控制的控制系统。主调节器的输出值作为副调节器的输入值，副调节器的输出直接作用于执行器。所以外回路是定值控制，内回路是随动控制[4]。串级控制系统原理如图3所示。

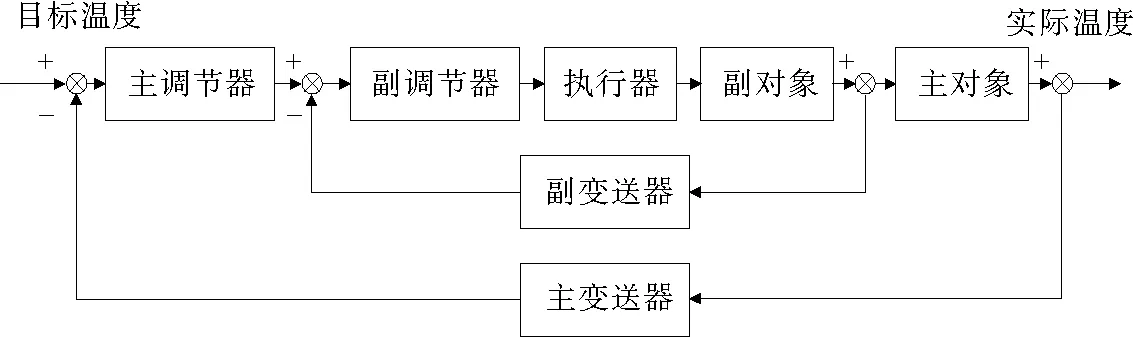
图3 串级控制系统原理图

串级控制系统与单回路控制系统相比，在结构上多了一个副回路，形成两个闭环回路，一个是定值控制系统的主回路，一个是随动控制的副回路。由于副回路的存在，串级控制系统可以更快速地克服干扰，使系统更快速地稳定下来。在控制过程中，按调节作用来分，副回路起粗调作用，而主回路起细调作用[11]。在电锅炉的出水温度控制中，因其具有大滞后、非线性的特性，且干扰量多，常规单回路控制系统无法满足条件，所以采用串级控制系统对电锅炉出水温度进行控制。

各部分近似传递函数包括：

1) 副对象处(导前区)传递函数

(1)

式中：K1为导前区的放大系数；T1、n1分别为导前区惯性环节的时间常数和阶数。

2) 主对象处(惰性区)传递函数

(2)

式中：K2为惰性区的放大系数；T2、n2分别为惰性区惯性环节的时间常数和阶数。

在串级控制系统中，主调节器和副调节器分工明确，协同控制。控制系统对主、副调节器的要求是不同的，主回路的要求一般较高，调节要细致，主调节器的控制应选取PI或PID控制，在本方法中主回路选择PID控制[14]；副回路要求控制的快速性，能够对系统的变化快速响应，一般情况下，会选取比例控制而不引入积分或微分控制。引入积分控制会使控制过程变慢，减弱副回路的快速控制作用；引入微分控制会使系统调节幅度过大，影响整个控制系统的稳定性。在本方法中，副回路选择比例控制。

PID控制是指将误差的比例通过叠加组合成控制量,对被控对象进行控制[15]。其控制规律为：

(3)

式中：Kp为比例系数，Ti为积分时间常数，Td为微分时间常数。

给定值r(t)与实际输出值y(t)误差：

e(t)=r(t)-y(t)。

(4)

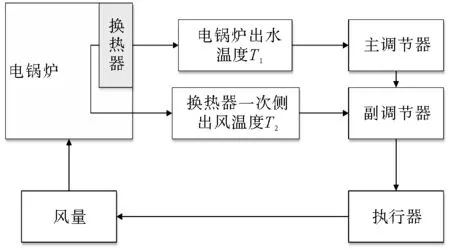
图4 电锅炉温度控制原理图

PID控制传递函数：

(5)

3 温度控制方法

3.1 控制方法

相变储能电锅炉的出水温度控制采用串级控制的思想，通过控制循环风机转速和调节阀调节循环风道风量，根据实际需要调整风量大小，实现对电锅炉出水温度的控制，其温度控制原理如图4所示。

串级控制系统的主变量为电锅炉出水温度T1，副变量为电锅炉换热器一次侧出风温度T2。副回路检测电锅炉换热器一次侧出风温度T2，调节阀开度调节循环风道风量，对T2进行调节；主回路检测电锅炉出水温度T1与目标值进行比较，变频风机和调节阀根据比较结果协调运作，调节循环风道风量，对电锅炉出水温度T1进行调节。主回路是对温度的细调，副回路是对温度的粗调。在主调节器作用之前，副调节器先作用一次，使电锅炉出水温度不会与目标温度T偏差太大，然后主调节器再次对出水温度进行调节，直至达到目标温度。控制流程图如图5所示。

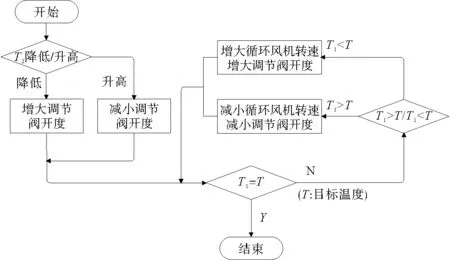
图5 控制流程图

当系统检测到换热器一次侧出风温度T2逐渐降低，说明用户端热量需求大，电锅炉出水温度T1随后逐渐降低，串级控制系统副回路发生作用，调节阀开度增大，使流向换热器处的风量增大，提供更多的热量，提高电锅炉出水温度T1。副回路作用过后，主回路检测电锅炉出水温度T1，与目标温度进行比较。若T1小于目标温度，则增大循环风机转速，继续增大调节阀开度，增大循环风道风量，为换热器处提供更多热量；若T1大于目标温度，则降低循环风机转速，减小调节阀开度，减少循环风道风量，降低流向换热器处的热量。

当系统检测到换热器一次侧出风温度T2逐渐升高，说明用户端热量需求小，电锅炉出水温度T1随后逐渐升高，串级控制系统副回路首先作用，调节阀开度减小，使流向换热器处的风量减少，降低流向换热器处的热量，降低电锅炉出水温度T1。副回路作用过后，主回路检测电锅炉出水温度T1，与目标温度进行比较。若T1大于目标温度，则降低循环风机转速，继续减小调节阀开度，减少循环风道风量，降低流向换热器处的热量；若T1小于目标温度，则增大循环风机转速，增大调节阀开度，增大循环风道风量，为换热器处提供更多热量。

相对于采用单回路控制的电锅炉系统，串级控制系统多了一条副回路、一个副被控对象T2。在串级控制系统中，T2的变化快于T1的变化，由于副回路的存在，系统会先对T2进行调节。由于电锅炉出水温度T1在一定情况下是跟随T2变化的，因此对T2的调节相当于提前对T1的变化进行调节。而电锅炉出水温度T1的变化具有滞后性，恰恰因为串级控制系统副回路中对T2的调节，使T1的变化得到提前调节，极大程度上缓解了T1的滞后性。

表1 函数模型

3.2 对象传递函数建模

根据文献[16]，传统蒸汽热锅炉副对象传递函数多为1～3阶惯性环节，主对象传递函数多为3～5阶惯性环节。而相变蓄热电锅炉虽然在控制方式有相似之处，但热交换模式却大相径庭，非线性与大滞后性尤为突出。以天津某地3 MWh谷电相变蓄热电锅炉为例，依据现场运行及实验数据在采用最小二乘法进行拟合，然后采用专用仿真软件验证，当主副对象惯性环节阶次同为3时，传递函数最佳。表1是系统在不同负荷情况下得到的函数模型。

3.3 以负荷在60%情况下系统各环节传递函数为例

系统主对象处传递函数为：

(6)

系统副对象处传递函数为：

(7)

系统内环闭路传递函数为：

(8)

串级系统内环多是提前调节、粗调、快调，所以多采用PI或P模式，本方法采用P控制。执行器传递函数Kz=1，两温度变送器传递函数分别为Wr1(s)=Wr2(s)=0.1。

系统外环闭路传递函数为：

(9)

其中Wc1(s)是外环PID的传递函数。

3.4 PID参数整定

PID控制系统由于其算法简单、具有较强的可靠性及鲁棒性，而得到了广泛应用，而其参数整定的研究也从未间断。目前大体分为两类：工程法与理论法。理论法是主要研究方向，主要指标是智能、自适应、自学习，根据系统环境的变化参数自我调整，但其算法复杂，对软硬件要求都很高，特别是小的自控系统实现非常困难。所以以齐格勒-尼可尔斯(Z-N)法则为基础的工程整定方法仍旧被广泛应用。本研究采用基于Z-N法则的临界比例增益试验法与特征方程逼近法。

1) 临界比例增益试验法

参数整定顺序先内环后外环，排除主副调节器的积分与比例环节，即只有比例控制Kp。具体做法是将比例系数Kp值由零逐渐增大到系统的输出首次呈现持续的等幅振荡，此时对应的Kp值称为临界增益，用Kc表示，并记下振荡周期Tc。然后根据表2中的公式，确定内环PID控制器参数Kp，Ti和Td[17]。内环参数确定后，以同样方式确定外环参数。试验得到：内环参数Kp=6.32；外环参数Kp=2.8，Ti=74.2，Td=18.55。

表2 Z-N法则第二法

2) 特征方程逼近法[17]

内环参数确定：根据公式(8)，得到闭环特征方程为(1+5.2s)3+8.1Kp2=0，令s=jω，得到jω(15.6-140.61ω2)-81.12ω2+1+0.81Kp2=0，解之得Kc=Kp2=9.88，ω=0.333 1，则Kp=0.5Kc=4.94；

外环参数确定：同理，依据确定的参数内环回路作为随动系统，确定外环参数。根据式(9)，得到闭环特征方程((1+5.2s)3+4)(1+24.6s)3+4.92Kp1=0，令s=jω，解之得Kc=Kp1=5.48，Wn=0.061，Tc=2π/Wn=103.0。根据表2可得，Kp=3.29，Ti=51.5，Td=12.88。

4 实验与仿真

依据第3节给出的某地蓄热电锅炉的数学模型，通过仿真对串级控制与单回路控制的控制性能进行分析；对比分析不同PID参数整定情况下的串级控制性能优劣。锅炉设计参数：供热面积为30 000 m2，出水温度目标值为80 ℃，换热器一次侧出风温度为150 ℃，风量为750 m3/h，供热流量为100 m3/h。

利用建Simulink软件对电锅炉的温度进行仿真，模拟电锅炉系统在启动后2 000 s内的出水温度变化。用一阶跃信号模拟电锅炉启动，Simulink仿真图如图6所示。电锅炉出水温度仿真曲线如图7所示，其中串级仿真1采用特征方程逼近法求得的参数，串级仿真2采用临界比例增益试验法求得的参数。

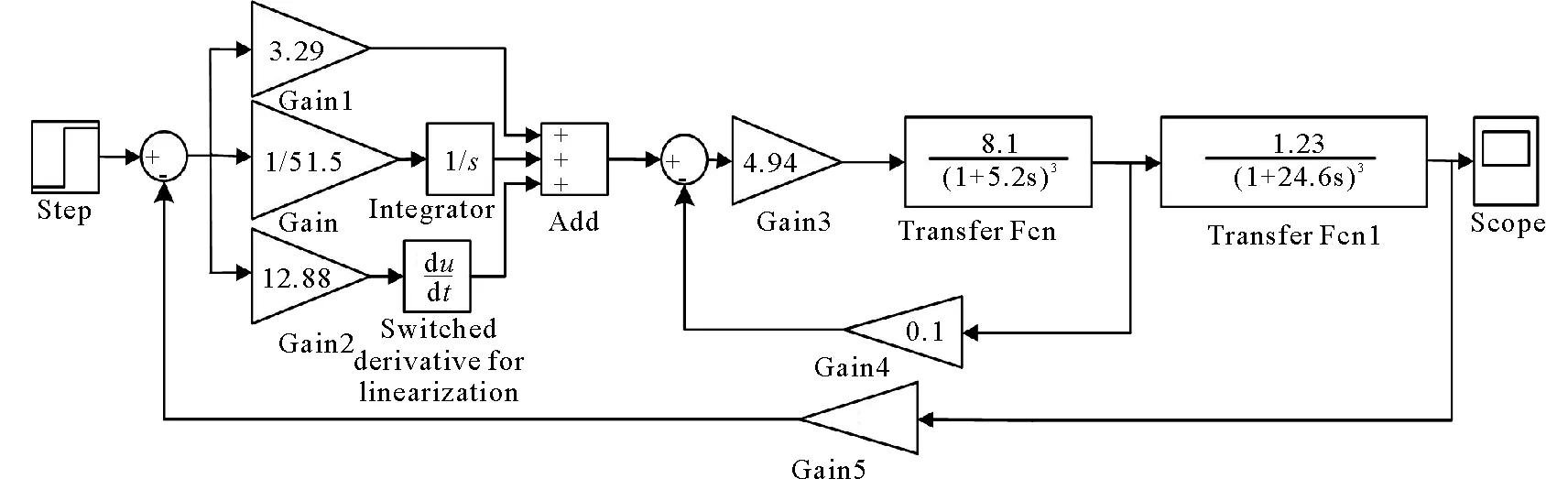
图6 串级控制系统Simulink仿真

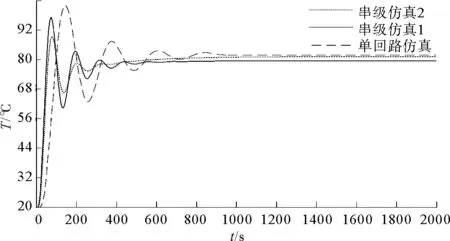
图7 电锅炉出水温度仿真曲线

在1 200 s时，加入一阶跃信号，模拟电锅炉系统备用风机启动时造成的干扰，Simulink仿真如图8所示。采用串级控制系统的抗干扰仿真曲线如图9所示，显示其抗干扰能力。

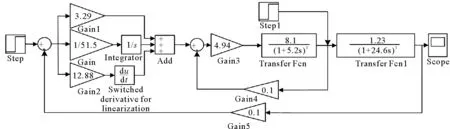
图8 增加干扰后Simulink仿真

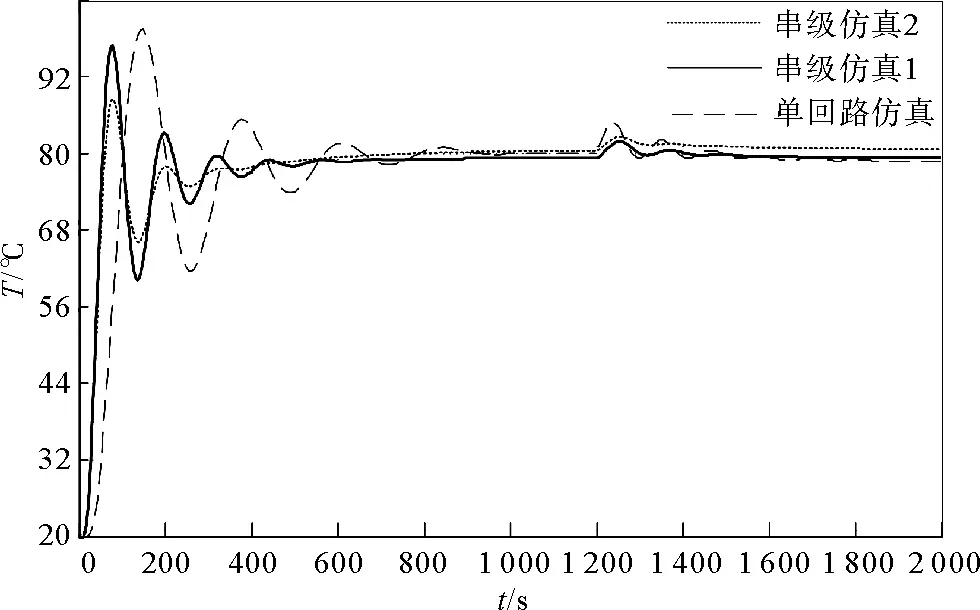
图9 加入干扰后的出水温度变化仿真图

5 结论

1) 通过实验与仿真，串级控制系统相对于单回路控制系统，其动态响应性能及抗干扰能力都具有明显优势。较好地验证了串级控制系统的提前预测、预控能力，克服了单回路控制系统在面对大滞后、非线性、复杂控制系统时响应速度及抗干扰能力差等方面的不足。

2) 通过仿真曲线1与仿真曲线2对比发现，不同的参数整定方法，参数会有差异，性能也略有差异，这种问题与计算误差和试验测试误差都有一定的关系，很难说孰优孰差，换一种控制环境或控制模型，其结果可能会发生改变。本研究采用临界比例增益法整定的参数，性能优于特征根逼近法。