中国家庭育儿成本

刘娜 李小瑛 颜璐

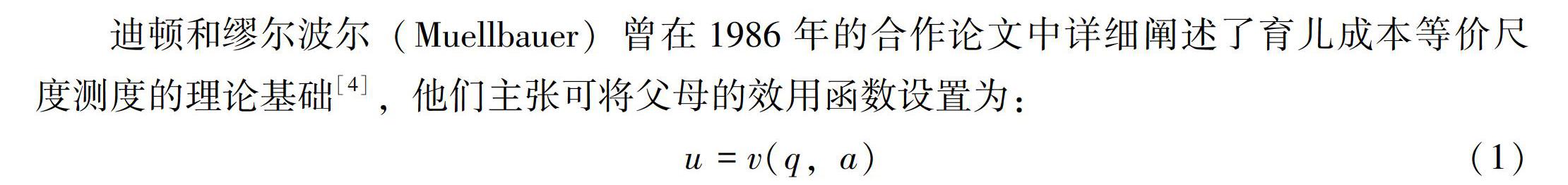
摘 要：利用2016年CLDS和CFPS 数据，基于等价尺度Engel模型法和Rothbarth模型法，精确估算了中国家庭孩童抚育成本。研究显示，与仅有两个成人没有孩子的家庭相比，一孩家庭总支出将提高63.91%至67.62%，二孩家庭总支出将提高139.28%至149.99%（孩均提高69.64%至75%），二孩抚育并未显现出“规模经济”。家庭育儿成本随孩子年龄增大而提高，城镇家庭育儿成本普遍高于农村家庭，城乡家庭间存在基于人口特征的差异化支出偏好。基于中国育儿成本等价尺度测度的政府差异化育儿津贴补助模拟分析表明，发放差异化育儿津贴可有效缓解家庭育儿经济负担并缩小家庭间收入差距。

关键词：育儿;生活成本;等价尺度;福利

中图分类号：C92-05   文献标识码： A   文章编号：1000-4149（2021）01-0050-18

DOI：10.3969/j.issn.1000-4149.2020.00.042

收稿日期：2020-03-22;修订日期：2020-07-05

基金项目：国家社会科学基金项目“生育政策调整、住户规模效应与中国家庭收入不平等研究”（16BJL041）。

作者简介：刘娜，湘潭大学商学院副教授，博士生导师;李小瑛，中山大学港澳珠江三角洲研究中心、粤港澳发展研究院副教授，博士生导师;颜璐，湘潭大学商学院硕士研究生。

The Child Costs in Chinese Family： A Welfare Estimate Using Equivalence Scale

LIU  Na1， LI  Xiaoying2，3， YAN  Lu1

（1.Business School，Xiangtan University， Xiangtan 411105， China;2.The

Center for Studies of Hong Kong， Macao and Pearl River Delta， Sun Yatsen

University， Guangzhou 510275， China;3.Institute of Guangdong， Hong Kong and

Macao Development Studies， Sun Yatsen University， Guangzhou 510275， China）

Abstract： Using 2016 CLDS and CFPS datasets， this essay accurately

estimates the household childcost in China using Equivalence Scale based on Engel Model and Rothbarth Model separately. It illustrates that， compared to childless couple， the total expenditure for onechild households in China usually rises from 63.91% to 67.62%， and 139.28% to 149.99% （69.64% to 75% per child） for the twochild households. There is no evidence for economies of scale in child breeding. In addition， the cost of children usually enhances when children grow up. It is generally higher in urban households than rural households， and there are various preferences in expenditure between urban and rural households based on demographic characteristic. The sinmlation analysis of government differentiated childcare allowance subsidy based on equivalent scale measure of childcare cost in China shows that， differentiated childrearing allowance can effectively alleviate the

economic burden of childrearing and narrow the income gap between families.

Keywords：child breeding;living costs;equivalence scale;welfare

一、引言

20世纪80年代以来实施的计划生育政策对控制我国人口规模起到了重要作用，但由此引发了超低生育率及随之而来的劳动年龄人口比重下降、人口老龄化加剧等严峻问题。鉴于对人口形势可能进一步恶化的谨慎预期，我国于2002年出台“双独二孩”政策，2013年进一步实施“单独二孩”政策，2016年再度全面放开二孩生育。然而，人口政策的逐步放宽并未带来生育率的大幅提升。“全面二孩”政策实施后我国人口出生率表现差强人意，从2016年12.96‰的高点下跌至2019年的10.48‰（見图1）。正如早前国家统计局局长马建堂所述，中国已步入“低生育率陷阱”

引自http：//www.caijing.com.cn/2011-04-28/110704539.html。为何中国人不愿意生育更多孩子？国家卫生和计划生育委员会（现国家卫生健康委员会）2015年生育意愿调查显示，因经济负担过重、太费精力、无人看护不愿生育第二个子女的分别占到被调查者的74.5%、61.1%、60.5%，经济压力是民众不愿意生育二孩的首要原因

引自http：//www.chinanews.com/gn/2017/01-22/8132414.shtml。深受重教传统影响的中国父母在子女身上历来倾情投入，而实施逾四十年的计划生育政策使家庭资源更集中配置在为数较少的孩童身上，社会平均育儿成本快速上涨。日益攀升的育儿经济压力无疑约束了民众的生育意愿和生育行为，很可能诱发当前我国的超低生育率现象。

事实上，孩童相当于纯“消费品”，抚育孩童必将提高家庭消费支出水平，使家庭承受更大经济压力[1]。抚育孩童究竟会在多大程度上影响家庭消费支出？长期以来，学界围绕科学测度家庭育儿成本已展开了广泛而深入的探讨，而等价尺度（Equivalence Scale）分析方法因其基于家庭食物支出份额等间接标准展开家庭福利比较，且指数化分析本身具有广泛的可比性，成为家庭育儿成本测度领域的主导研究范式。

等价尺度分析允许人们在衡量社会福利水平时考虑家庭规模和构成的不同，基于等值收入这一共同衡量标准来度量每个家庭及家庭成员的福利。诺贝尔经济学奖得主迪顿（Deaton）将等价尺度定义为：在效用不变、价格不变前提下，将具有人口特征a的家庭（如三口之家）的生活成本同具有人口特征aR的参照家庭（如一夫一妻家庭）的生活成本关联起来的生活成本指数[2]。早在1895年，恩格尔（Engel）就曾将食物支出份额作为家庭福利的间接表示进而提出著名的恩格尔系数，这便是等价尺度分析的最初表现形式[3]。此后，在众多经济学家的不断推动下，育儿成本等价尺度研究逐步发展壮大，延伸发展出Rothbarth模型、PraisHouthakker模型、Barten模型、Gorman模型和Muellbauer模型等，形成了较为完善的理论体系。

本文拟利用我国2016年家庭入户调查数据，基于Engel 模型和Rothbarth模型展开中国家庭育儿成本的等价尺度测度，试图回答抚育孩童究竟在多大程度上影响中国家庭消费支出这一问题，并尝试从经济成本视角深入理解我国超低生育率现状。

二、等价尺度概念界定及测度模型演化历程

1. 等价尺度概念界定

等价尺度是在效用不变、价格不变的前提下，将具有人口特征a的家庭的生活成本，同某个具有人口特征aR的参照家庭的生活成本关联起来的生活成本指数[2]。它可对家庭“规模经济”进行准确描述，指数化人口构成对家庭总支出的影响，进而支撑家庭福利的比较。文献基于等价尺度方法展开的福利对比分析已广泛运用于收入不平等与贫困、税收和社会福利以及性别歧视等论题，但育儿成本的等价尺度测度成为其最重要的应用领域之一。

迪顿和缪尔波尔（Muellbauer）曾在1986年的合作论文中详细阐述了育儿成本等价尺度测度的理论基础[4]，他们主张可将父母的效用函数设置为：

u=v（q，a）（1）

其中，q是一组代表家庭消费水平的变量，a是一组人口特征变量（如家庭中不同年龄和性别成员的数量等）。父母是家庭决策者，是孩子来到这个家庭之前和之后一直存在的家庭成员。父母可以从孩子身上，以及自己和孩子的消费中获得效用。基于式（1）可获得家庭成本（支出）函数c（u，p，a），它表示家庭在价格水平p、人口构成a前提下为达到效用水平u必须付出的最小支出额。若uR和pR是参照效用和价格水平，则具有人口结构a1的家庭较之具有人口结构a0的参照家庭的消费增加值可描述为：

C=c（uR，pR，a1）-c（uR，pR，a0）（2）

换言之，我们可通过设置下述比率指表，即等价尺度，来表征两个不同家庭的相对生活成本：

E=c（uR，pR，a1）c（uR，pR，ao）（3）

为便于比较，两个家庭的效用u被设定在同一水平，且其面对的价格水平p也是即定的。

在上述设置基础上，只需恰当选取效用参照标准即可精确测度一国育儿成本等价尺度水平。迪顿和缪尔波尔在其1986年论文中便利用斯里兰卡和印度尼西亚数据展开了测度分析。基于Engel食物支出份额福利比较法，以只有夫妻二人没有孩子的家庭为参照家庭，他们测算出1969—1970年的斯里兰卡，1孩家庭消费总支出是参照家庭的1.41倍，2孩家庭消费总支出是参照家庭的1.77倍。而在1978年的印度尼西亚，拥有1个5岁以下（1个5岁以上）孩子家庭的消费总支出是参照家庭的1.45倍（1.58倍），拥有2个5岁以下（2个5岁以上）孩子家庭的消费总支出是参照家庭的1.86倍（2.22倍）[4]。可见，等价尺度的确能精确展示不同人口特征家庭的相对福利水平，有利于开展更为细致、严谨的家庭福利比较。

2. 育儿成本等价尺度测度模型演化

德国统计学家恩格尔早在19世纪中叶探讨收入增加对消费支出可能产生的影响时发现了一条规律：贫困家庭食物支出占比相对较高，富裕家庭物支出占比则相对较小。推而广之，贫穷国家的国民，其平均食物支出占比会相对更高，而富裕国家的国民其平均食物支出占比则会相对更小[3]。自此以后，食物支出占比被命名为恩格尔系数（Engel Coefficient），成为国家之间、家庭之间福利比较的重要指标，恩格尔系数的出现及广泛应用完成了等价尺度生活成本分析的历史首秀。

其后，众多学者沿着基于生活成本指数开展福利对比分析的方向不断推进，在育儿成本等价尺度测度上更发展出承前启后的系列测度模型。在恩格尔基于食物支出占比分析家庭育儿成本的基础上，罗斯巴斯（Rothbarth）进一步考虑用成人商品总支出衡量成人福利水平。他选择一组典型的成人商品，假定新生儿仅通过“类收入效应”影响成人商品的总支出，因而将生育之后成人商品支出总额恢复到生育之前支出水平所需给付的补偿额即为家庭育儿成本[5];塞德斯切克（Sydenstricker）和金（King）则认为Engel模型中假定所有人面对的商品价格一致是不合理的，每一种商品都应有各自不同的等价尺度[6]。普锐斯（Prais）和侯斯塔克（Houthakker）在其基础上进行了完善，在商品之间不存在替代性的假设条件下，主张区分特定商品消费和其他商品消费，提出需区分估计特定等价尺度和一般等价尺度，形成PraisHouthakker模型[7];巴顿（Barten）则针对PraisHouthakker模型商品相对价格不发生变化这一假设条件，在商品之间存在替代性的设置下考虑价格差异可能产生的影响，构造了将各类商品等价尺度直接引入效用函数的Barten模型[8];而针对Barten模型的过度替代性缺陷，格曼（Gorman）提出应把某些随家庭特征变化的固定成本纳入成本函数，以描述家庭构成存在的准价格效应和一部分固定成本效应[9];缪尔波尔则主张家庭每个成员对各类商品都应有特定的等价尺度，应在Barten模型的基础上以成年夫妇组成的家庭为参照对象，用估计家庭与参照家庭的最小生活成本之比来定义等价尺度[10]。自此，以家庭为参照对象、充分考虑家庭規模特征和商品价格水平的等价尺度测度已深入到家庭基本需求的比较分析中，这有利于展开更为综合、广泛的福利比较研究。

与一般理论体系的演进一致，等价尺度研究方法亦是沿袭前人理论构架、逐步放宽模型假设，使指数分析愈来愈贴近现实为理解现实提供更精准的解释。在众多学者的推动下，育儿成本等价尺度研究方法逐步演进，形成了较为完善的理论体系（见图2）[11]，也为我们精确测度中国家庭孩童抚育成本提供了可靠的方法支持。

在基于等价尺度测度孩童抚育成本的已有文献中，迪顿和缪尔波尔1986年的测度最为经典。他们利用斯里兰卡和印度尼西亚数据详细测度了两国育儿成本等价尺度水平，具体方法上则同时采用了Engel食物份额法、Rothbarth成人商品法和GormanBarten估计。测度结果表明，Engel方法通常夸大了孩童抚育真实成本，而Rothbarth方法存在一定程度的低估，GormanBarten估计值则介于（大于）Engel估计和（小于）Rothbarth估计之间。然而在实际应用中，GormanBarten模型的参数估计总是极其困难，因此迪顿和缪尔波尔认为 Rothbarth和Engel方法在未来仍将被广泛使用[4]。此外，为更贴近现实，Muellbauer模型对家庭需求函数和成本函数进行了更为复杂的设置。这固然有利于获得精准的测度结果，但考虑实证研究中经常出现关键数据缺失、测算过程异常复杂等经验问题，缪尔波尔个人也认为基础模型的一般结论仍是非常可靠的[12]。有鉴于此，我们在后面的分析中将分别采用Engel食物份额法和Rothbarth成人商品法，展开中国孩童抚育成本的等价尺度估计。

三、中国育儿成本的等价尺度测度

1. Engel测度方法

恩格尔将食物支出份额作为家庭福利的间接表示，认为成人生活水平与家庭食物支出占比相关[3]。因此，新生儿成本可以

用父母为保持与生育前完全相同的家庭食物支出占比而多付出的开销来估算。

秉承恩格尔做法此处假定，若家庭食物支出占比相同，则两个拥有不同数目和年龄孩子的家庭中的成人是擁有相同福利水平的。设食物支出占比为ωf，则有：

ωf=∑i∈flnc（u，p，a）lnpi=ψ（u，p，a）（4）

若在效用水平一致、价格水平相同前提下，拥有人口特征a1家庭 此处指较参照家庭多一个孩子的家庭。的食物支出占比等于或高于具有a0人口特征的参照家庭 即满足尼科尔森

（Nicholson）1976年文献中所提及的前提条件[13]。，则家庭生育孩子后为能达到生育前家庭食物支出比水平而付出的全部新增支出即为孩子的成本。

依据Working - Leser模型，食物支出比是家庭总支出对数的线性函数[14-15]。沿袭迪顿和缪尔波尔做法[4]，我们将人口特征植入W - L模型，估计函数设置为：

ωf=α-βlnxn+∑Jj=1γjnj+ε（5）

其中，nj是家庭不同年龄分组j（j=1，2，…，J）的人数，n是家庭总人口数，x为家庭总支出，ε为误差项。α，β和γ是各项系数。

若设参照家庭食物支出比为ω0f，x0和x*分别为参照家庭和人口更多家庭h在拥有相同福利水平（即相同食物支出比）时的总支出，则（x*-x0）的差值就是人口更多家庭h较之参照家庭为孩子付出的成本。那么，等价尺度就可以被简单描述为x*与x0的比值（x*/x0）。联系式（5），当家庭食物支出比相等时x*可以定义为：

α-βlnx*nh+∑γjnhj=α-βln

x0n0+∑γjn0j（6）

因此，Engel等价尺度 EhE=x*/x0可以估算为：

EhE=nhn0exp

∑JIγjβ（nhj-n0j）（7）

利用式（5）和式（7），我们即可基于Engel模型度量一个国家或地区的育儿成本等价尺度水平。

需特别说明的是，因成人福利水平事实上来自于多样化“消费”组合（譬如，成人可通过游乐休闲消费等提升自己的效用水平），成人食物支出份额能很好表征成人福利水平这一关键假设并不完全符合现实，因而基于Engel方法得到的育儿成本等价尺度是一个理论上偏高的估计值[4]。迪顿和缪尔波尔对斯里兰卡和印度尼西亚的测度亦说明，采用Engel方法度量的等价尺度数值上的确相对偏高。

2. Rothbarth测度方法

与恩格尔方法以保持相同食物支出比为福利标准不同，罗斯巴斯（Rothbarth）方法是以维持相同成人商品支出水平为基准展开测度的，以父母为保持和生育前完全相同的成人商品支出而多付出的开销来核算孩子成本。罗斯巴斯将家庭中所有物品和劳务消费分为两类，即仅由成人消费的“成人商品”和通常由成人及孩子共同消费的“其他商品”，成人的效用仅由成人商品的消费决定。他认为，孩子的出现存在“类收入效应”（incomelike effects），将影响成人对成人商品的消费。如果父母为新生儿补偿了足够支出，不论孩子数量多少家庭成人商品的消费都没有改变，则此种情况下父母总体福利水平与生育孩子前保持一致[5]。罗斯巴斯曾使用包括从奢侈品到储蓄在内的多种商品类型定义成人商品，后来的研究者们则更多采用烟和酒作为成人商品，以测算等价尺度水平。

遵从罗斯巴斯基本做法，此处将家庭的成人商品消费函数设置为：

Ca=α+βlnCt+∑γjnj+ε（8）

其中，Ca为家庭成人商品消费额，lnCt为家庭总消费额的对数，nj仍是家庭不同年龄分组j（j=1，2，…，J）的人数，ε是误差项。α，β和γ为各项系数。于是，某一年龄组j的1个孩子的等价尺度可以由以下公式求得：

EhE=nhn0exp∑JI-γjβ（nhj-n0j）（9）

利用公式（8）和公式（9），我们可基于Rothbarth方法来度量一个国家的育儿成本等价尺度水平。

然而，仅以成人商品表征成人福利水平，此假设也并不完全符合现实（譬如，孩子食物支出占比越多，其父母福利水平也可能更高）。同时，受数据严格限制，在实际测算中通常难以获得奢侈品或煙酒等成人商品的精准支出水平，而更为常见的做法是用家庭消费中除食品以外的非食品支出来表征成人商品消费量。这种处理方法虽便于测度操作，但事实上只对非常贫困的家庭具有严格代表性，却将高估中等家庭和富裕家庭的成人商品支出量，进而造成对孩童抚育成本的低估[4]。因此，Rothbarth方法测度的育儿成本等价尺度会是一个理论上偏低的估计值。

3. 等价尺度测度结果

本部分将分别使用2016年中国劳动力动态调查（China Laborforce Dynamics Survey，CLDS）数据和中国家庭动态跟踪调查（China Family Panel Studies，CFPS）数据，利用Engel 和Rothbarth两种测度方法，以仅有两个成人没有孩子的家庭为参照，测度中国育儿成本等价尺度水平。

中国劳动力动态调查数据由中山大学社会科学调查中心执行，聚焦中国劳动力现状与变迁，2016年样本覆盖全国 29 个省市（除港澳台、西藏、海南外）。中国家庭动态跟踪调查数据则由北京大学中国社会科学调查中心执行，数据库以家庭为单位关注中国社会发展变迁，2016年样本覆盖全国31个省（区）、直辖市（除港澳台外）。CLDS与CFPS 数据均基于入户调查获取，是当前公开可得的微观调查数据中提供我国家庭人口构成及消费支出信息最丰富的数据库，为本文测度中国育儿成本等价尺度提供了难得的数据基础。在清理了城镇及农村家庭人口、支出、户主及家庭特征信息，处理了缺漏值，并比照国家统计局家庭年收入和支出数据进行必要调整后 去除“食品支出占比”最高和最低5%家庭样本。，我们的有效样本包括来自CLDS 2016的8632个家庭和CFPS 2016的 5085个家庭。样本家庭成人数在1—7之间，孩子数在0—5之间，均为同住家庭成员。

表1展示了样本主要描述统计信息。在城乡分布上，CLDS数据样本量相当，而CFPS数据农村样本偏多。需要说明的是，CLDS和CFPS 2016年数据主要在2016年7—8月采集，收支统计上CLDS数据以“2015年”为统计时限，CFPS则以“过去12个月”为时限。国家统计局数据显示 我国居民家庭收入、支出和家庭食品支出占比数据均来自国家统计局网站，http：//data.stats.gov.cn/easyquery.htm？cn=C01，2015年我国居民人均消费支出为15712.41元，其中城镇和农村居民人均消费支出分别为21392.36元和9222.59元（当年全国居民人均可支配收入为21966.19元，城镇和农村居民人均可支配收入分别为31194.83元和11421.71元）。对比官方数据，CLDS和CFPS样本家庭消费支出和收入水平与全国平均水平基本持平，因此本文样本在家庭经济层面具有全国代表性。CLDS数据库更为关注劳动年龄人口家庭，其有孩家庭样本为3702个（一孩家庭2268个、二孩家庭1156个、三孩及以上家庭217个），占样本总量的42.89%。CFPS数据则为家庭综合调查数据，有孩家庭为3319个（一孩家庭2128个、二孩家庭972个、三孩及以上家庭219个），达样本总量的65.27%。总体上，农村样本家庭较城镇样本家庭拥有更多孩子，这符合我国城乡家庭曾受差别化生育政策约束的国情。进一步关注家庭福利水平

恩格尔

系数，即“家庭食品支出占比”。国家统计局数据显示，2010年至2014年我国城镇居民家庭恩格尔系数在35.0%至37.9%间浮动，农村居民家庭恩格尔系数则在37.7%至43.7%之间，总体呈微幅波动下降走势。本文CLDS和CFPS家庭样本中，农村样本家庭食品支出占比为38.36%和41.25%，位于较为合理的区间，但城镇样本家庭食品支出占比为41.90%和41.46%，数值上稍有偏高（见表1） CLDS样本家庭食品支出占比在0.0571至0.8471之间，CFPS样本家庭则在0.0857至0.9000之间。为保障测度结果的稳健性，我们将同时基于CLDS和CFPS家庭样本对中国育儿成本等价尺度水平展开平行估计。

依据Engel模型 和Rothbarth模型测度要求，我们首先分别基于（5）式和（8）式展开回归分析。除必需的基本控制变量外，在数据允许的范围内我们还控制了户主性别、年龄、民族、是否党员、健康状况、就业状况，家庭年总收入（对数）、用水来源、用电稳定性、家户编号以及家庭所在省份（区）、城乡地区哑变量 利用CLDS 2016数据展开的回归控制了户主、家庭及地区系列变量。但受数据限制CFPS 2016回归仅控制了家庭和地区系列变量。后续对应回归分析的变量控制均与此一致。获得（5）式和（8）式回归系数后再分别基于（7）式和（9）式测算我国等价尺度水平。如前所述，Rothbarth方法需基于家庭成人商品的消费来展开分析。由于CLDS和CFPS数据均未提供详细到个人的消费信息，无法剥离成人支出，因此我们借鉴迪顿和缪尔波尔的做法[4]，将家庭非食品支出视为成人商品展开研究，以辅助与Engel测度结果的对比分析。

表2集中展示了中国等价尺度测度结果。受生育政策的严格限制，最多生育两个孩子是中国家庭的普遍现状，因而我们仅报告最多两个孩子家庭的育儿成本等价尺度水平。左方三列集中展示了CLDS数据结果，右方三列则为CFPS数据估计。A部分结果基于Engel方法获得，B部分则是基于Rothbarth方法的估计值。A和B两部分下还各含两个测度值子集，其一为仅区分家庭孩子数量的综合测度，其二为结合孩子数量和年龄构成的细化估值。本文所有测度均以仅有两个成人没有孩子的家庭为参照，估计表中孩子为0的横行表示参照家庭水平，其等价尺度值为1。

首先看A部分Engel模型测度结果。总体来看，分别利用CLDS和CFPS数据展开的中国育儿成本等价尺度测度数值上十分接近、走势上基本趋同。CLDS数据分析显示，当家庭拥有1个孩子时，全样本等价尺度为1.7309。即相较于参照家庭，一孩家庭总支出将增加73.09%（0.7309）。当家庭拥有2个孩子时，全样本等价尺度为2.6631，意为以参照家庭为基准，两孩家庭总支出将增加166.31%（1.6631），其中每个孩子将使家庭总支出增加83.16%。CFPS数据估计则表明，以参照家庭为基准，一孩家庭总支出将增加71.27%，两孩家庭总支出则增加160.74%（孩均增加80.37%）。基于CLDS和CFPS数据对城乡差异的考察表明，城镇家庭育儿成本普遍高于农村家庭。以一孩家庭为例，CLDS数据测度显示城镇家庭总支出将较参照家庭增加84.71%，这高于农村家庭67.28%的增幅。CFPS数据结果则表明，相同情况下城镇家庭总支出将增加77.74%，同样高于农村家庭69.12%的增幅;再来看考虑孩子数目和年龄的细化估值。测度表明，随着孩子年龄逐步增大，家庭总支出会逐步增加，家庭将为年龄较大的孩子支付相对更多的成本。这一结果与我们的日常感知是一致的。以CFPS数据全样本为例，若家中分别增加年龄为0—5岁、6—11岁、12—17岁的1个孩子，则家庭总支出水平将较参照家庭分别提高66.08%、73.67%和79.41%。若分别增加三个年龄段中相应年龄段的2个孩子，则家庭将因每个孩子而分别增加72.59%、84.05%和93.07%的总支出。可见，我国二孩家庭育儿边际成本相较一孩家庭更高，并没有展现出成本上的“规模经济”。

B部分Rothbarth测度结果与理论预期一致，数值上较Engel测度普遍更低。两种方法分析结果总体趋于一致，但因采用家庭非食物支出而非烟、酒等确切成人商品来展开分析，细分孩子数量和年龄的Rothbarth估计并没有Engel测度稳定。结合Rothbarth及Engel测度结果，我们至少可以证实以下三个基本结论：其一，与参照家庭相比较，有孩家庭的家庭总支出水平普遍更高。其二，家庭为孩子支付的经济成本随孩子年龄的增大和孩子数目的增加而逐步提升。其三，二孩家庭育儿边际成本普遍高于一孩家庭。然而，利用CLDS和CFPS数据分别展开的Rothbarth估计却在城乡对比上展示了与Engel测度不完全一致的结果，城镇家庭等价尺度与农村家庭等价尺度孰高孰低未有定论。排除数据自身的抽样差异，这仍可能与上述Rothbarth测度中采用家庭非食品支出表征成人商品消费额可能引致偏误有关。后续我们的研究还发现，我国城乡家庭间存在着基于人口特征的差异化支出偏好，城乡家庭对不同福利指标的敏感度不同也可能引致城乡对比分析结果不稳定。

现有利用等价尺度方法测度孩童抚育成本的国际研究也主要基于Engel测度和Rothbarth测度展开。文献显示，以参照家庭新添1个孩子为例，20世纪末英国家庭的等价尺度水平在1.39（Engel）与1.26（Rothbarth）之间、澳大利亚家庭等价尺度在1.502（Engel）与1.180（Rothbarth）之间[16]。而1981年的希腊家庭，0—5岁孩童等价尺度为1.299（Engel）与1.091（Rothbarth）之间，6—13岁孩童等价尺度为1.352（Engel）与1.130（Rothbarth）之间[17]。在同样重视孩童教育的近邻日本，基于1993年至1999年数据估算的家庭等价尺度Rothbarth测度在1.386—1.475之间[18]。

这些文献测度结果均展示出Engel測度值高于Rothbarth测度值，以及孩童抚育成本随着孩子年龄增加而升高的基本特征，这与本文的测度结果一致。但我们利用2016年CLDS数据获得的1.7309（Engel）与1.6214（Rothbarth）、CFPS数据测度的1.7127（Engel）与1.5654（Rothbarth）与前述各国在20世纪末测度的等价尺度相比，在绝对数值上是明显更高的。然而，跨度几十年的国别数据使各测度结果间没有完全的可比性，数据的缺乏亦使我们无法查询、测算中国更早时期的育儿等价尺度以展开对比。但近期有报告显示，20世纪以来孩童抚育成本在全球范围内均有显著提升，且着重表现在孩童照护服务价格上涨和孩童教育支出攀升上 详见http：//www.sohu.com/a/198959141_751398。在崇尚家文化、极其重视孩童教育的中国，经济上的改革开放显著提升了中国家庭消费能力，而强劲的有效购买力与严格执行的计划生育政策（特别是早期执行的“独生子女”政策）交织结合，在过去40年间很可能共同推动了中国孩童抚育成本的快速上涨。

如前述在理论分析和国际比较中提及的，Engel测度是一个偏高估计，而Rothbarth测度是一个偏低估计。为便于更简单明了地展示中国等价尺度水平，我们在表3中呈现了基于估值偏高的Engel测度与估值偏低的Rothbarth测度均值结果，提供了一个基于算术平均法获得的折中参考值。依据均值测算，我国2016年一孩家庭等价尺度水平在1.6391至1.6762之间，二孩家庭等价尺度水平在2.3928至2.4999之间。即与仅有两个成人没有孩子的参照家庭相比较，一孩家庭的家庭总支出将提高63.91%至67.62%，二孩家庭的家庭总支出将提高139.28%至149.99%（孩均提高69.64%至75%） 表3同步给出了不同孩童数目和年龄结构家庭的中国育儿成本等价尺度参考均值，若需测算已育家庭再多生育（或抚育）一个孩童的成本，则可在表3中选取生育前和生育后两种情况对应的测度系数，进行差值计算即可得相较于参照家庭增加的边际成本。

四、人口构成对家庭支出影响的分解

1. 方法介绍

迪顿、 路兹卡斯特罗（RuizCastillo）和托马斯（Thomas）1989年曾进一步考察具有不同人口特征的家庭成员在不同类型商品消费上的差异及其相互影响，探讨了家庭消费的可拆分性[19]。本部分我们将借鉴他们的做法，考察人口构成对中国家庭不同类型商品消费的影响，并关注此影响在城乡家庭间的差异。

按照0—5岁、6—11岁、12—17岁、18—24岁、25—44岁、45—60岁及60岁以上年龄标准，我们将每个样本家庭的家庭成员分别划归到7个不同年龄组 对18岁以下未成年家庭成员，按照学龄前（0—5岁）、小学学习阶段（6—11岁）和中学学习阶段（12—17岁）划分。成年家庭成员则按照继续教育（大学/职业学校/硕博）学习阶段（18—24岁）、成婚和生育阶段（25—44岁）、中年阶段（45—60岁）及退休阶段（60岁以上）分组。，用不同年龄段人口数来表征家庭人口构成。在重点关注的人口构成对家庭消费的影响上，我们秉承迪顿等人的方法[19]，使用支出等价比（outlay equivalent ratios）来展开相关分析。对某一普通商品（normal commodity）i和某个r年龄段家庭成员而言，支出等价比πir可定义为：

πir=（piqi）/nr（piqi）/x·nx（10）

它描述了每增加一个r年龄段家庭成员时家庭对商品i的边际需求，测度了该家庭为达到与未新添成员时相同的总需求水平而支付的额外开销。

我們将基于人口特征可拆分性而扩展的弹性估计函数展开基础回归分析，而后核算支出等价比数值，据此做出人口构成对家庭不同类型商品消费影响的基本判断。扩展的弹性估计函数设置如下：

ωi=piqix=αi+βiln

xn+ηilnn+∑J-1j=1γij

njn+δi·Z+ui（11）

其中，ωi表示商品i在家庭总支出中的占比，pi为i商品价格，qi为家庭对i商品的消费量，x为家庭总支出，n为家庭总人口数，nj是家庭中j年龄段人数，Z为前述已列出的各项户主、家庭及地区系列控制变量。利用（11）式回归分析结果，我们可参照如下计算支出等价比的公式：

πir=（ηi-βi）+γir-∑Jj=1γij（nj/n）βi+ωi（12）

获得支出等价比πir后，依据估值正负符号我们可判断，为保持家庭总需求水平不变，新增一个r年龄段家庭成员可能对家庭i商品消费产生影响的弹性方向，即家庭为维持原有总需求水平应增加还是减少对i商品的消费。而不同年龄段家庭成员对同一商品i消费的弹性正负差异则可显示出该家庭基于人口特征的差异化支出偏好。

2. 人口构成对家庭分项支出影响的测度结果

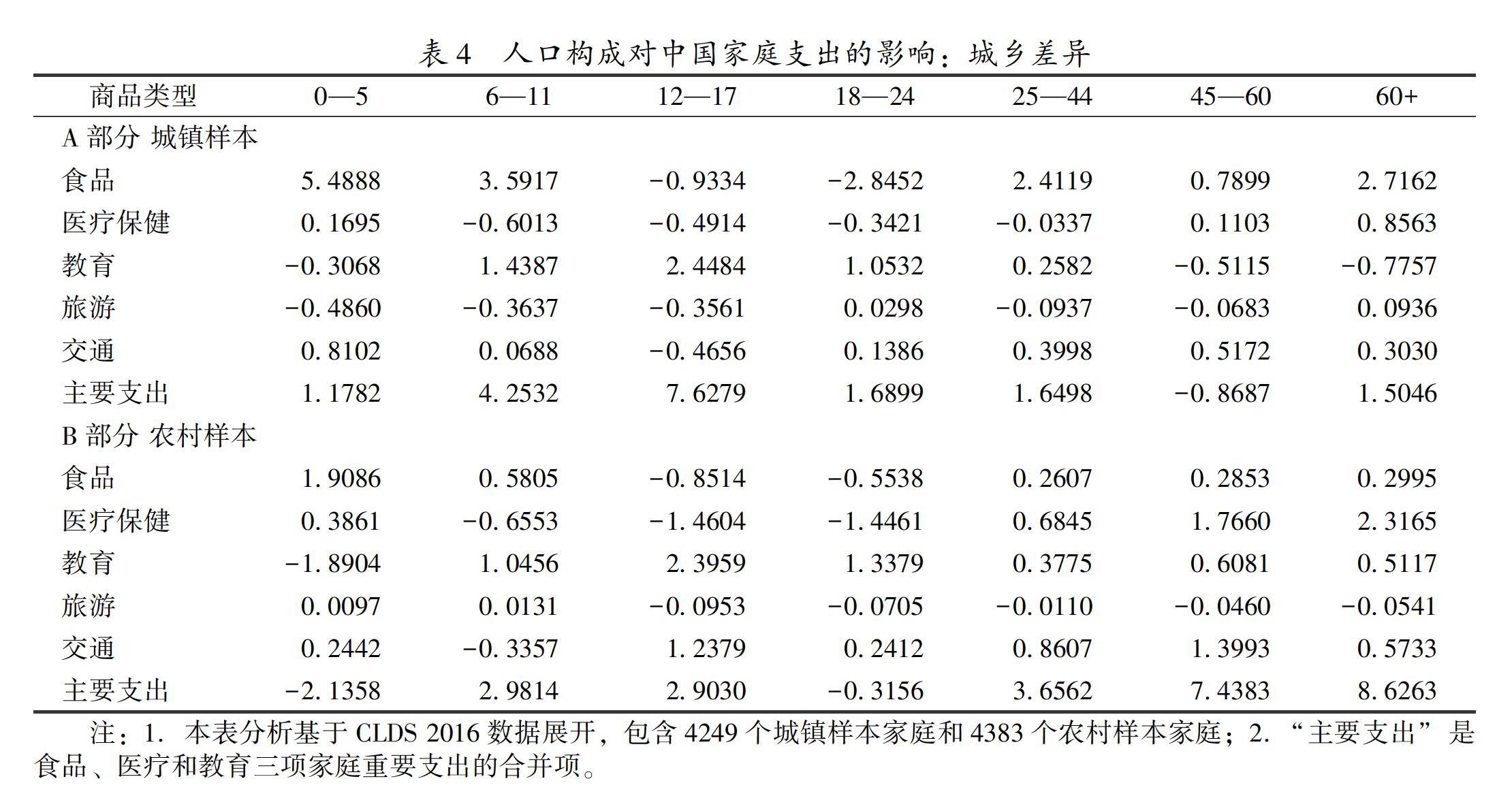
借鉴迪顿等人方法[19]，我们初步估计了家庭不同年龄段人口对家庭支出可能产生的影响。因CLDS 2016数据库8632个有效样本较CFPS 2016数据库5085个有效样本样本量更大，且在家庭食品、教育、医疗、旅游、交通等分项支出上缺损更少、信息更为完备，我们利用CLDS 2016数据分别考察了不同年龄段家庭成员对家庭食品、教育、医疗等分项支出的影响，同时我们将食品、医疗和教育三项重要开支合并为“主要支出”项，以考察不同年龄段人口对家庭消费的综合影响。相关结果展示于表4。

表4中A部分城镇样本分析显示，在家庭总需求不变前提下，新添年幼家庭成员会使城镇家庭增加食品和医疗保健消费，减少教育和旅游支出。而新增年长成员时城镇家庭将产生更多食品、医疗保健和旅游支出，减少教育消费。若家中求学年龄段成员增加，则城镇家庭会明显提升教育支出水平。B部分对农村样本展开的考察结果与城镇家庭分析十分接近。而与城镇家庭不同的是，在家庭总需求不变前提下，农村家庭新添年幼成员会增加微量旅游支出。这或与农民工家庭向城镇地区临时迁移有关。同时，农村家庭新增年长成员不会像城镇家庭一样对旅游支出造成增量影响。综上所述，在家庭总需求不变情况下，不同年龄段家庭成员对家庭不同类型商品的消费确实产生了差异影响。对家庭主要支出（食品、医疗、教

育支出合并项）的进一步考察表明，城镇家庭中幼年和青年成员对家庭支出具有更大影响力，农村家庭支出除对幼年成员较为敏感外更多会受到中老年家庭成员的影响。我国城乡家庭的确存在基于人口特征的差异化家庭支出偏好。

回到等价尺度Engel测度和Rothbarth测度的城乡差异讨论上。上述分析表明，我国农村家庭中老年成员对家庭消费支出具有较大影响力。而Rothbarth测度则是以家庭成人商品消费额为福利基准展开分析的，因此在Rothbarth测度中，农村家庭较城镇家庭会对孩子消费支出更敏感，这在一定程度上导致了基于CLDS数据的农村家庭Rothbarth估计高于城镇家庭估计的结果。事实上，在利用CFPS数据展开的Rothbarth估计中，农村家庭测度结果并未显著低于城镇家庭，这亦不排除城乡家庭差异化支出偏好的影响。综上所述，本文对中国等价尺度的Rothbarth估计结果可能受到了城乡家庭差异化支出偏好的影响。由此，以Engel测度为准绳，结合Rothbarth模型和Engel模型估计，对中国等价尺度水平展开综合分析和评价是十分必要的。

五、基于等价尺度估计的我国差异化育儿津贴补助效果模拟

我国计划生育政策已实施逾40年。在“严格控制人口数量”方针指导下，国家对女性劳动者生育行为给予了较少关注，仅在1994年12月原劳动部颁布的《企业职工生育保险试行办法》中规定，企业应以上年度月平均工资为计发标准为女职工发放一次性生育津贴 生育津贴具体计算公式为“职工所在用人单位月缴费平均工资/30天×假期天数”。21世纪以来，我国人口出生率逐步走低，虽有“双独二孩”、“单独二孩”和“全面二孩”政策陆续出台，但人口出生率依旧颓势不减。于是，社会各界呼吁持续放松我国计生政策，实施更为积极的生育鼓励政策的呼声不绝于耳。效仿欧美发达国家为生育家庭提供育儿津贴成为最具借鉴意义和可操作性的政策调整方向之一。本节拟基于前述中国育儿成本等价尺度估值，模拟政府实施差异化育儿津贴补助可能对家庭收入产生的影响。

欧美发达国家为鼓励生育，普遍有按照收入额定比例发放的生育津贴补助。此处，我们仍将以2016年CLDS数据为例，以表3中国家庭育儿成本等价尺度参考均值数为基准，模拟政府对低收入家庭实施育儿津贴补助可能对家庭收入产生的影响，其中家庭抚育孩童数目及年龄结构将成为生育津贴水平高低的重要决策依据。以家庭收入及人口构成信息是否缺失为依据我们对2016年CLDS数据进行梳理，获得13260个有效家庭样本。进一步查询国家统计局《中国统计年鉴》得知，2015年我国居民人均可支配收入为21966元，其中城镇居民31195元，农村居民11422元 居民人均可支配收入数据来自国家统计局网站，http：//data.stats.gov.cn/easyquery.htm？cn=C01。接下来，依据样本家庭孩童数目及年龄构成，以表3 CLDS数据测度均值为基准，我们分别模拟对人均收入低于21916元的全样本家庭、低于31195元的城镇家庭、低于11422元的农村家庭实行差异化生育津贴补助，拟以3%、5%、10%、15%四档支出额定百分比进行补助，估算低收入家庭因孩童抚育每年可获得的育儿补助金额。例如，年人均收入低于21916元的家庭若新添一个新生儿则其参照等价尺度水平为1.5333（查表3 CLDS数据全样本家庭“a0=1 a1=0 a2 =0”项数值），即相较于参照家庭该家庭总支出将增加53.33%（0.5333）。以CLDS 2016数据全样本中仅有两个成人没有孩子的家庭（参照家庭）年平均支出43714.57元为基数 参照家庭为仅有两个成人没有孩子的家庭，CLDS 2016数据全样本参照家庭年平均支出为43714.57元，城镇参照家庭为57548.88元，农村家庭为32469.50元。，结合等价尺度测度支出增加比率为53.33%，可测算出该家庭分别按照3%比例发放的育儿津贴为43714.57×53.33%×3%=699元/年，而按照5%、10%和15%比例发放的育儿津贴则分别为1166元/年、2331元/年和3497元/年。遵循此法，不同家庭差异情况下的育儿补助金额估算汇总于表5。

发放差异化育儿津贴即向城乡家庭直接注资，这不仅提高了城乡家庭收入水平，亦定向中和了家庭育儿成本，缓解了家庭经济压力。同时，因津贴发放在不同家庭间存在结构性差异，很可能引发家庭间收入差距的变化。因此，在利用中国育儿成本等价尺度测算不同家庭育儿补助金基础上，我们就发放差异化育儿津贴可能对家庭收入基尼系数产生的影响进行了进一步模拟。在对受益家庭进行模拟补助后，我们分别核算了补助前与补助后全样本、城镇样本及农村样本的家庭收入基尼系数，相关数据展示于表6。结果显示，相较于未给予差异化育儿津贴的情况，按育儿支出3%比例补助将使全样本家庭收入基尼系数降低0.0042，按5%比例补助则降低0.0069，将补助比例提高至10%时基尼系数缩小0.0136，而补助比例提高至15%时基尼系数降至0.0199。实行差异化补助后样本家庭收入基尼系数全部低于补助前，这说明该项定向差异化补助有效缓解了家庭之间因孩童抚育差异而拉大的收入差距，有利于家庭经济、社会福利的均衡发展。

综合而言，基于中国育儿成本等价尺度测度的政府差异化育儿津贴补助模拟分析表明，在国家财政可以承受的范围内发放差异化育儿津贴将有效降低家庭育儿成本、缓解育儿经济负担，同时亦有利于缩小家庭之间的收入差距。但我们也发现，因城乡家庭收入（支出）绝对水平差异较大，以支出额定百分比展开育儿补助时农村家庭获取的补助金额远低于城镇家庭。建议在制定相关政策时充分考虑城乡差异，将育儿补助向相对劣势的农村家庭倾斜。譬如，基于相对更高的支出定额百分比给予农村家庭以育儿津贴补助。

六、结论

本文分别利用2016年CLDS和CFPS 家庭入户调查数据，基于等价尺度测度的Engel模型和Rothbarth模型，精确估计了中国家庭孩童抚育成本，以期从经济成本视角深入理解我国当前超低生育率现象。分析表明，以仅有两个成人没有孩子的家庭为参照，2016年我国一孩家庭等价尺度水平在1.6391至1.6762之间，二孩家庭等价尺度水平在2.3928至2.4999之间。即与仅有两个成人没有孩子的参照家庭相比，一孩家庭总支出将提高63.91%至67.62%，二孩家庭总支出将提高139.28%至149.99%（孩均提高69.64%至75%）。可见，我国二孩家庭育儿边际成本相较一孩家庭更高，并未显现抚育成本上的“规模经济”。分析还发现，家庭为孩子支付的经济成本随孩子年龄的增大逐步提高，城镇家庭育儿成本普遍高于农村家庭;基于CLDS数据消费明细信息，我们进一步考察了不同年龄段家庭成员对家庭分项支出的影响。研究发现，城镇家庭中的幼年和青年成员对家庭支出具有更大影响力，而农村家庭支出除对幼年成员较为敏感外更多会受到中老年家庭成员的影响。我国城乡家庭之间的确存在基于人口特征的差异化家庭支出偏好;基于中国育儿成本等价尺度测度的政府差异化育儿津贴补助模拟分析表明，在国家财政可以承受的范围内发放差异化育儿津贴将有效缓解育儿家庭经济负担，降低育儿经济成本，同时有利于缩小家庭之间的实际收入差距。

等价尺度是基于等值收入的共同衡量标准来度量每个家庭及家庭成员福利的生活成本指数，本文则是基于等价尺度测度Engel模型和Rothbarth模型估计中国孩童抚育成本的一次有益尝试。然而，受入户调查数据样本量限制，我们的测度结果也可能存在一定偏误。期望未来可进一步基于国家统计局城调队、农调队调查数据以及人口普查数据等大样本数据，应用更为复杂算法下的优化等价尺度测度模型展开更为精准的育儿成本等价尺度测度。

近年来，我国人口出生率快速下滑，这很可能引发未来劳动年龄人口锐减、人口老龄化加剧等问题，对我国跨越中等收入陷阱、实现经济长期稳定发展形成威胁。本文基于等价尺度分析方法对我国家庭孩童抚育经济成本进行的测度表明，我国家庭孩童抚育经济成本相对较高。欲扭转我国超低生育率现状，应首先考虑采取系列措施降低家庭育儿成本。我们建议，可考虑以中国育儿成本等价尺度为基准，依据家庭抚育孩童的数目和年龄特征为不同家庭提供差异化抚育补助金或托幼、保育等公共服务，以减轻家庭孩童抚育直接成本。应特别关注处于相对劣势的农村家庭，使相关政策措施向农村家庭倾斜;同时，可考虑设立专门机构对我国家庭育儿成本展开实时动态监控，以启发对我国二孩家庭育儿边际成本呈现“非规模经济”等现象的理解。此外，建议结合我国国情尽快推行“生育友好型”政策体系。可借鉴北欧及英美等國经验，实施旨在帮助劳动者平衡工作与家庭、鼓励女性就业和推动男性参与儿童照料的双薪型家庭政策以有效鼓励生育。

参考文献：

[1]BECKER G S.A treatise on the family[M]. Cambridge， MA： Harvard University Press，1991：121-122.

[2]DEATON A S， MUELLBAUER J. Economics and consumer behavior[M]. New York： Cambridge University Press，1980：205.

[3]ENGEL E. Die lebenskosten belgischer arbeiterfamilien fruher und jertzt[J]. International Statistical Institute Bulletin，1895， 9：1-74.

[4]DEATON A S， MUELLBAUER J.On measuring child cost： with applications to poor countries[J]. Journal of Political Economy， 1986，94（4）： 720-744.

[5]ROTHBARTH E. A note on a method of determining equivalent income for families of different composition[M]//CHARLES M. Wartime Patterns of Saving and Spending. Cambridge： Cambridge University Press，1943：897-899.

[6]SYDENSTRICKER E，KING W L.The measurement of the economic status of families[J]. American Statistical Association，1921，17：824-857.

[7]PRAIS S，HOUTHAKKER H.The analysis of family budgets[M].

Cambridge： Cambridge University Press，1955：147-160.

[8]BARTEN A P.Family composition， prices and expenditure patterns[M]//HART P E， MILLS G， WHITAKER J K.  Econometric Analysis for National Economic Planning， London： Butterworths， 1964，277-292.

[9]GORMAN W M.Tricks with utility function[M]//ARTIS M J， NOBAY A R. Essays in Economic Analysis， Proceedings of the 1975 AUTE Conference. Cambridge： Cambridge University Press， 1976：211-213.

[10]MUELLBAUER J.Can we base welfare comparisons across households on behaviour？[R].  presented at SSRC Economic Theory Study Group， Mimeo， 1976.

[11]劉娜，颜璐. 等价尺度福利比较的模型发展与经验应用——兼评家庭育儿成本测度研究进展[J].消费经济，2020（4）：85-95.

[12]MUELLBAUER J.Testing the Barten model of household composition effects and the cost of children[J]. Economic Journal，1977，87（347）：460-487.

[13]NICHOLSON J L.Appraisal of different methods of estimating equivalence scales and their results[J].Review of Income and Wealth， 1976，22（1）： 1-11.

[14]WORKING H. Statistical law of family expenditure[J].Journal of the American Statistical Association，1943，221（38）： 43-56.

[15]LESER C E V.Forms of Engel functions[J]. Econometrica，1963，32（4）：694-703.

[16]VAN DE VEN J. Demand based equivalence scale estimates for Australia and the UK[R].National Institute of Economic and Social Research Working Paper，2003.

[17]TSAKLOGLO P.Estimation and comparison of two simple models of equivalence scales for the cost of children[J].Economic Journal，1991，101（405）：343-357.

[18]OYAMA MASAKO. Measuring cost of children using equivalence scale on Japanese panel data[J]. Applied Economics Letters， 2006，13（7）：409-415.

[19]DEATON A S J，RUIZCASTILLO D，THOMAS H.The influence of household composition on household expenditure patterns： theory and Spanish evidence[J].Journal of Political Economy， 1989，97（1）： 179-200.

[责任编辑 方 志]