中国海域及邻区地震时间分布特征研究1

徐伟进 李雪婧 谢卓娟 吕悦军 高战武

1）中国地震局地球物理研究所，强地震学研究室，北京 100081

2）国家自然灾害防治研究院，地震灾害研究室，北京 100085

3）中国地震灾害防御中心，北京 100029

引言

地震时间分布模型是进行地震预测和地震危险性分析的重要理论基础，分析海域地震时间分布特征是进行海域地震危险性分析的重要研究内容。地震的发生在时间上符合泊松模型是当前概率地震危险性分析和地震预测中广泛接受的基本假设。泊松模型表示地震发生是相互独立的，即本次地震发生在时间上不受上次地震的影响，也不会对下次地震造成影响。地震时间独立分布模型包含泊松模型、双泊松模型、分段泊松模型、更新模型以及特征地震模型等（Cornell，1968；Gardner 等，1974；Schwartz 等，1984；胡聿贤，1990；Console 等，2003），其中泊松模型在地震学和工程地震学中应用广泛。地震学家们针对地震时间分布是否符合泊松模型做了大量统计检验工作（Gardner 等，1974；Bufe 等，2005；Michael，2011；Shearer 等，2012；Parsons 等，2012），目前中国、美国等国家在地震区划和地震危险性分析中均采用泊松模型（高孟潭，1996；潘华等，2013；Petersen 等，2014）。

相对于地震的时间独立模型，还有用于描述地震时间分布的时间相依模型，时间相依模型依据Reid（1910）提出的弹性回跳理论。弹性回跳理论认为地震发生是断层应变能渐进且连续的积累过程，当该断层出现突然的应变释放时就会发生构造地震，地震将大大减轻地壳的应变，在稳定的构造力作用下，压力慢慢地重新累积变大，最终发生下次地震。按照弹性回跳理论，断层上本次地震的发生受上次地震的影响，同样对下次地震产生影响，地震是时间相依的。近几十年来，科学家们使用不同地区的地震目录对地震时间相依性进行了实证研究，发现在许多情况下地震时间分布并不符合泊松模型，而时间相依模型能够更好地描述地震的时间分布特征（Utsu，1984；Nishenko 等，1987；Ogata，1991；Tripathi，2006；Sharma 等，2010；Ellsworth 等，2015）。科学家们提出了采用伽马模型（Gamma）、对数正态模型（Lognormal）、威布尔模型（Weibul）以及布朗过程时间模型（Brownian Passage Time，BPT）描述地震时间分布特征（Utsu，1984；Matthews 等，2002；Tripathi，2006；Pasari 等，2015，2018；Bajaj 等，2019），这些模型为地震预测和地震危险性分析提供了重要的理论支撑。

本研究中，以中国海域统一地震目录为基础资料，以泊松模型（指数分布）、伽马模型、对数正态模型、威布尔模型以及布朗过程时间模型为目标模型，回归了各模型参数，并通过AIC、BIC 判定准则和K-S 检验选择能够描述海域地震活动时间分布特征的最优模型。采用扩散熵分析（Diffusion Entropy Analysis，DEA）和标准差分析（Standard Deviation Analysis，SDA）方法对中国海域地震时间丛集特征和时间相关性进行研究。

1 数据、模型与方法

1.1 数据

海域地震事件记录是进行海域地震活动特征分析、海域地震危险性分析以及海域地震灾害预测等的重要基础数据，近几十年来，随着地震观测技术的提高和更多地震台网的布设，我国及周边国家、地区均记录了丰富的海域地震事件。地震学家收集了我国海域及周边国家、地区的地震台网记录，经过分析和整理，编制了我国海域统一地震目录，共计61 285 条地震事件（Xie 等，2021），该地震目录为进行我国海域地震危险性分析提供了重要的基础资料。本研究使用的海域地震目录是Xie 等（2021）分析整理的中国海域统一地震目录（图1（a））。Xie 等（2021）还对海域地震目录做了震级转换和完整性分析等工作，本研究中直接采用其海域地震时间完整性分析结果。使用Gardner 等（1974）得出的时空窗法删除了地震目录中的余震事件，该方法被广泛应用于地震区划图编制和地震活动性分析中的余震删除（Shearer 等，2012；Daub 等，2012；Petersen 等，2014）。删除余震后，还剩29 450 条主震事件，使用删除余震后的主震目录研究地震时间分布特征。

根据新划分的中国海域及领区地震带（图1（b）），以地震带为单元研究了海域地震时间分布特征。海域及领区地震带是进行海域地震活动性参数计算的基本单元，研究海域地震带地震时间分布特征对海域地震活动性参数的确定具有重要科学意义。

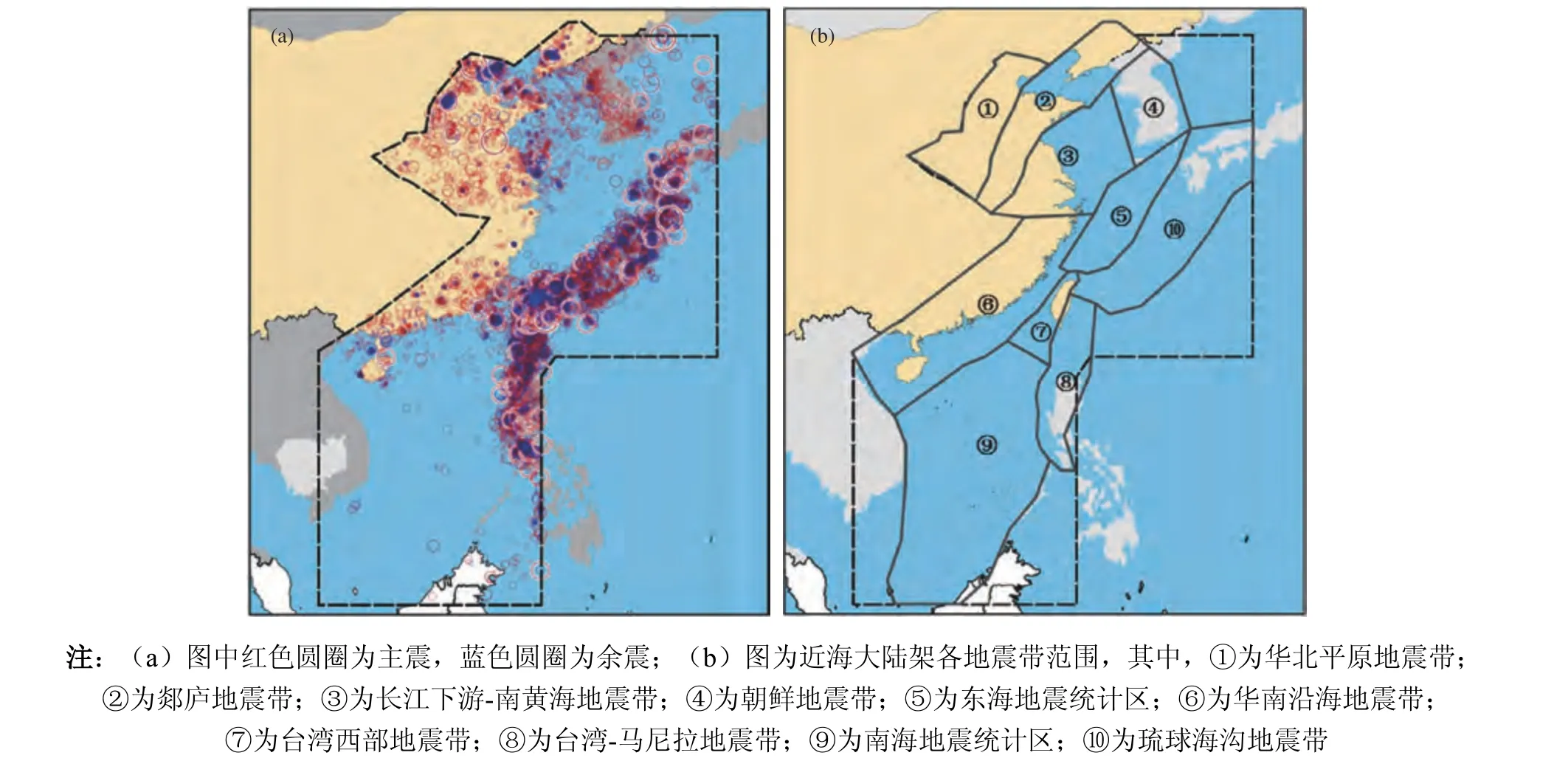
图1 中国海域及邻区地震分布Fig. 1 Earthquake distribution in China sea areas and adjacent areas

1.2 模型

本研究中选择泊松模型（指数分布）、伽马模型、对数正态模型、威布尔模型以及布朗过程时间模型作为参考分布模型，通过统计检验选择能够描述海域地震事件分布特征的最优模型。

（1）指数模型（指数分布）

指数分布是无记忆分布，可由指数分布在极端情况下推导得出，地震学家们通过检验地震时间间隔是否符合指数分布判断地震是否符合指数分布模型。指数分布概率密度函数为：

（4）威布尔（Weibull）模型由Weibull 等（1951）提出，Kagan（1997）认为该模型可以用于评估地震的复发概率。Weibull 概率密度函数f(x)表达式如下：

1.3 方法

采用扩散熵分析和标准差分析方法研究中国海域地震的时间丛集特征和时间相关性。DEA 法是Scafetta等（2004）在计算青少年生育现象时首先采用的，该方法在是否为高斯过程的情况下还是在变异数为无穷大的情况下，都能得到正确的标度参数。此后，该方法被广泛应用于分析不同地区地震的时间分布特征（Jiménez 等，2006；Zhou 等，2016）。Mega 等（2003）将DEA 应用于解释1976-2002 年加州地区不同地震丛集在时间上的分布关系，得出加州地区大尺度时间上的地震丛集和下个地震丛集具有相关性。Tsai 等（2008）用该方法分析了台湾地区地震与地震之间的相关性，发现台湾地区地震时间概率密度函数的标度值为0.83。

DEA 方法简述如下：设定单位时间Δt，将地震序列分成m个单位时间序列ξ i，设定门槛值k，当第i个单位时间内地震个数大于k时，ξ i=1，否则ξi=0。以t为窗口宽度，移动窗口，每次移动1 个单位时间，由n=0 到n=m-t开始移动，共生成m-t+1 道轨迹，在第n道轨迹，窗口内所有ξi总和为：

2 时间分布模型结果分析

以中国海域地震目录为基本输入，采用极大似然估计方法，回归了上文介绍的各模型参数。为选出最优模型，采用赤池信息准则（Akaike Information Criterion，AIC）、贝叶斯信息准则（Bayesian Information Criterion，BIC）以及K-S 检验判断模型拟合优度。AIC 和BIC 的定义分别为：

式中，k为模型参数个数；L为模型似然函数；n为样本量。训练模型时，增加参数数量相当于增加模型复杂度，会增大似然函数，也会导致过拟合现象，针对该问题，AIC 和BIC 均引入与模型参数个数相关的惩罚项，BIC 的惩罚项较AIC 的惩罚项大，考虑了样本数量，样本数量过多时，可有效防止模型精度过高造成的模型复杂度过高。从一组可供选择的模型中选择最佳模型时，通常选择AIC 或BIC 最小的模型。

表1 为根据整个中国海域及邻区地震目录回归得到的各模型参数值和模型拟合优度判定准则参数值。对于5.0 级以上地震，从表1 中可以看出，指数分布、威布尔分布以及伽马分布的AIC、BIC 以及K-S 检验值相近，其中威布尔分布具有最小的AIC 和BIC，指数分布具有最小的K-S 检验值（K-S 检验值表示地震经验分布与理论模型的差异，该值越小表示越接近），这意味M≥5 级地震不拒绝时间独立性的假设，但也具有一定的时间相关性。对于6.0 和7.0 级以上的地震，根据BIC 和K-S 检验值，可判定指数分布能够最优地表达海域地震的时间分布特征。由图2 的累积分布函数曲线可以看出，指数分布、威布尔分布以及伽马分布与实际数据吻合较好，对数正态分布和布朗过程时间分布与实际数据吻合较差。由上述分析可知，对于整个中国海域及邻区，指数分布能够最佳描述地震的时间分布特征，威布尔分布和伽马分布与实际观测数据吻合良好，但具有2 个参数，模型相对复杂。

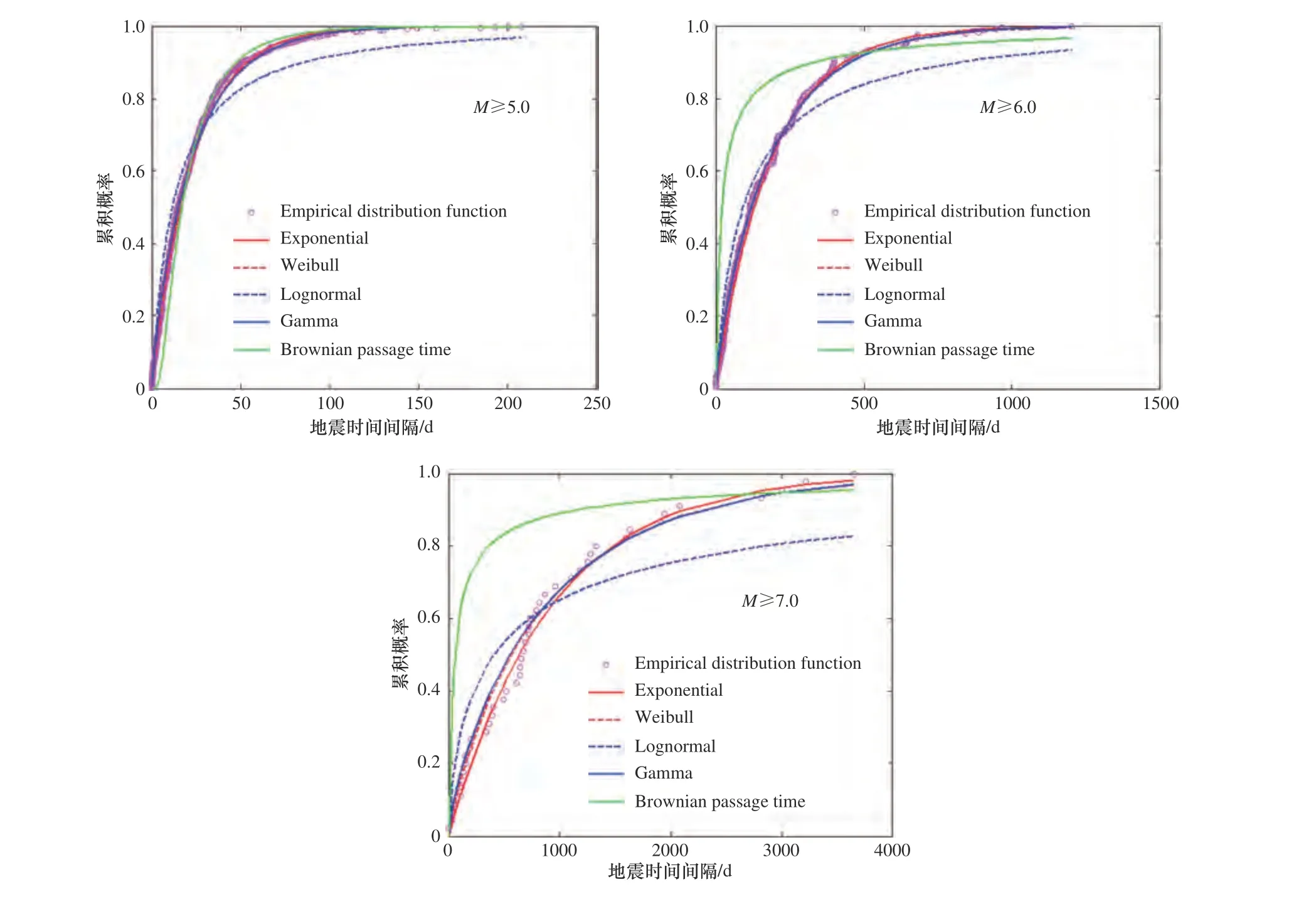
图2 中国海域及邻区不同震级地震的时间间隔累积经验分布函数及其对应的5 个模型累积分布函数Fig. 2 The cumulative empirical distribution function of the time interval of M≥5, 6, 7 earthquakes in the Sea area of China and adjacent areas and the cumulative distribution function of the corresponding five models

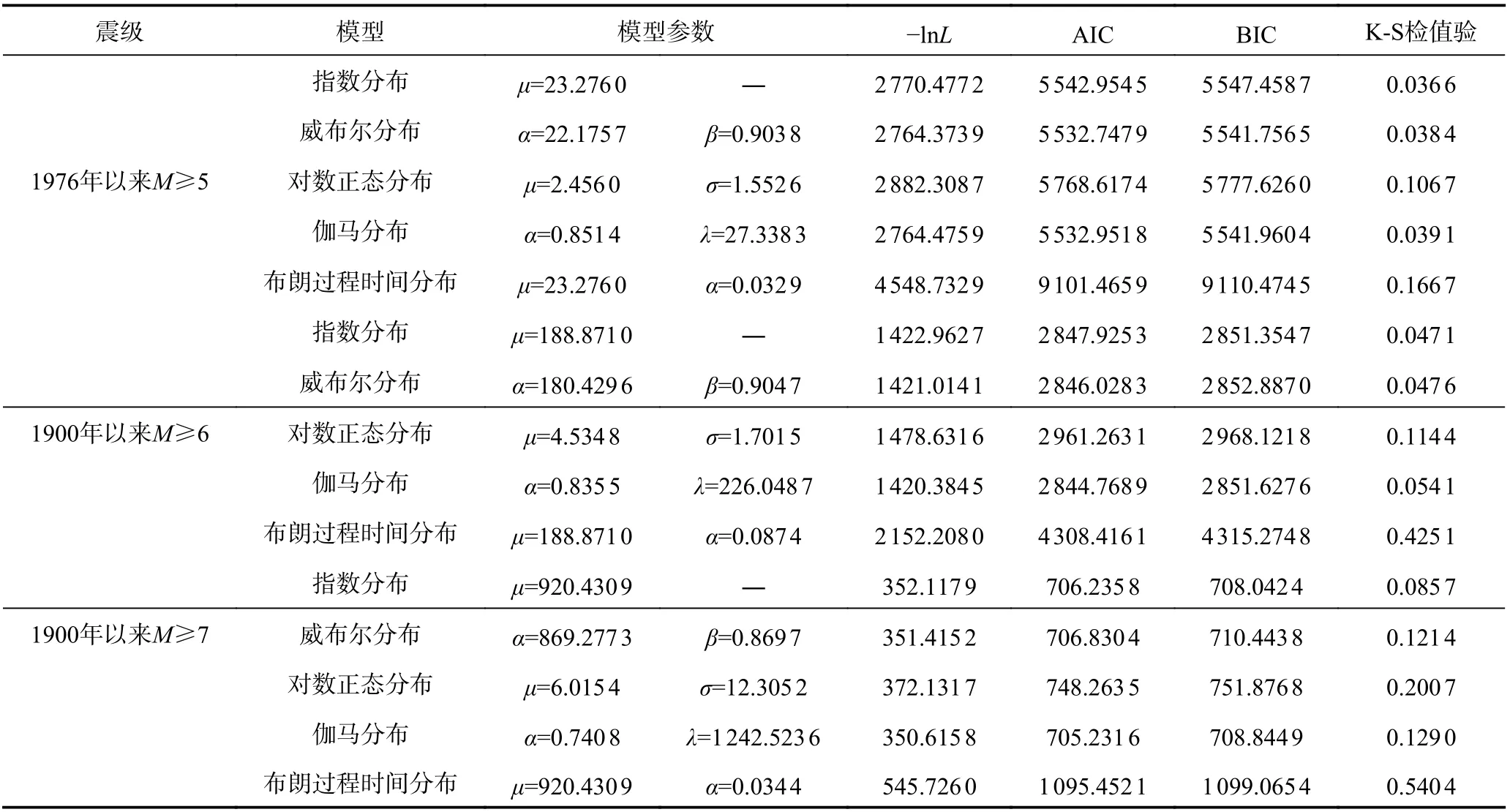
表1 中国海域及邻区模型参数及AIC、BIC 和K-S 检验值Table 1 Model parameters and AIC, BIC and K-S test results for earthquakes in China Sea and adjacent areas

表2 为根据华南沿海地震带地震目录回归得到的各模型参数值和模型拟合优度判定准则参数值。从AIC、BIC 和K-S 检验值上看，对于M≥4 级的地震，指数分布、威布尔分布和伽马分布均表现优良，模型间差异较小，K-S 检验接受地震时间间隔分布符合这3 种分布的假设；对于M≥5 级的地震，指数分布被判定为最优模型，威布尔分布和伽马分布也有良好表现；对于M≥6 的地震，K-S 检验显示所有模型均不拒绝时间独立性的假设，所有模型的AIC 和BIC 判定准则值均非常接近，特别是对于M≥4 和M≥5 级地震表现较差的对数正态分布和布朗过程时间分布，对于M≥6 级的地震表现优良，拟合优度好于威布尔分布和伽马分布。这意味着在发震构造特征相似的地震带内，大地震时间分布模型可用对数正态分布和布朗过程时间分布描述，这与国际上的研究结果相似。

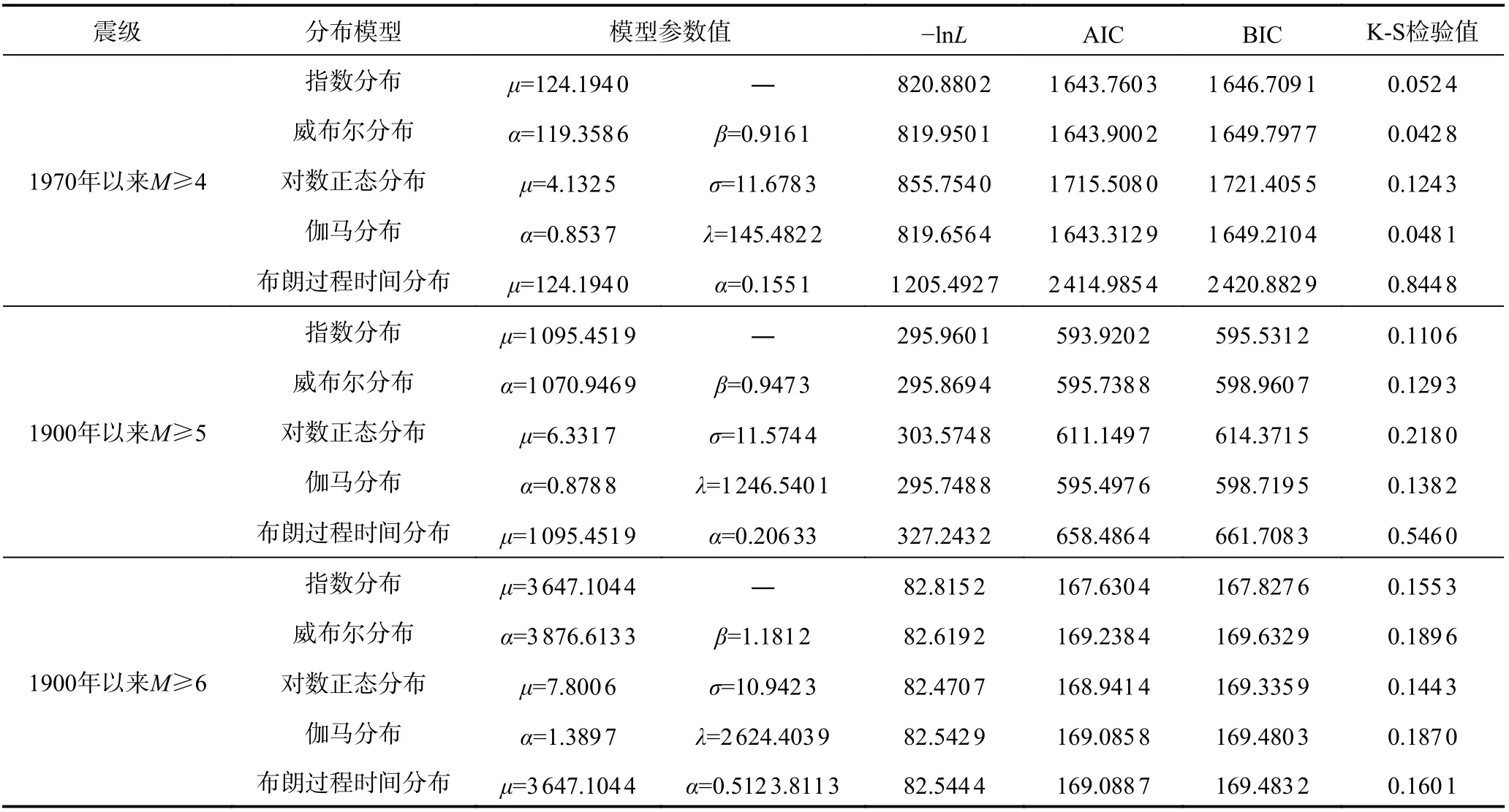
表2 华南沿海地震带模型参数及AIC、BIC 和K-S 检验值Table 2 Model parameters and AIC, BIC and K-S test results for earthquakes in South China Coastal seismic zone

表3 为根据台湾西部地震带的地震目录回归得到的各模型参数值和模型拟合优度判定准则结果。从AIC、BIC 和K-S 检验值上看，对于M≥4 和M≥5 级的地震，指数分布为最优分布，威布尔分布和伽马分布的拟合优度较好；对于M≥6.0 级的地震，正态对数分布和布朗过程时间分布拟合优度最好。这再次说明对于大地震，采用对数正态分布、布朗过程时间分布等模型来描述其时间分布特征更合适。

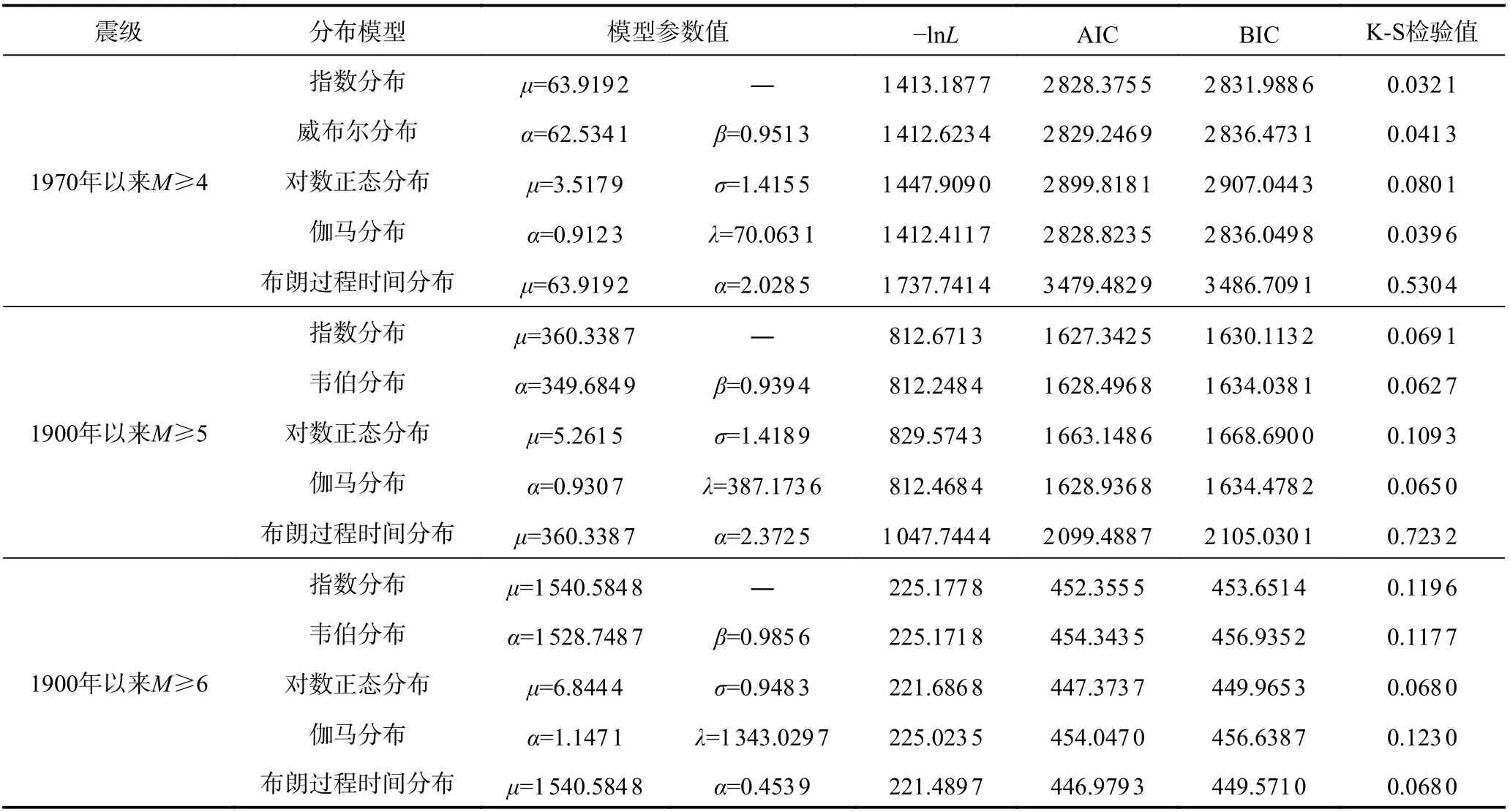
表3 台湾西部地震带模型参数及AIC、BIC 和K-S 检验值Table 3 Model parameters and AIC, BIC and K-S test results for earthquakes in the western Taiwan earthquake zone

表4 为根据台湾-马尼拉海沟地震带地震目录回归得到的各模型参数值和模型拟合优度判定准则参数值。从AIC、BIC 和K-S 检验值上看，对于M≥5 级的地震，威布尔分布拟合优度最好，伽马分布与威布尔分布较接近；对于M≥6 级的地震，指数分布为最优分布，威布尔分布和伽马分布表现较好；对于M≥7 级的地震，综合判定指数分布为最优模型，威布尔分布和伽马分布具有较好的拟合优度。从地震事件分布模型上可以看出，在该地震带内5 级以上地震具有较强的时间相依性，6 级以上地震可接受指数分布假设，但也具有一定的时间相关性。这是由于台湾-马尼拉海沟地震带地震活动非常强烈，经常发生8 级左右的地震，大震的发生对稍小震级地震具有一定影响，且震级越小所受影响越大。

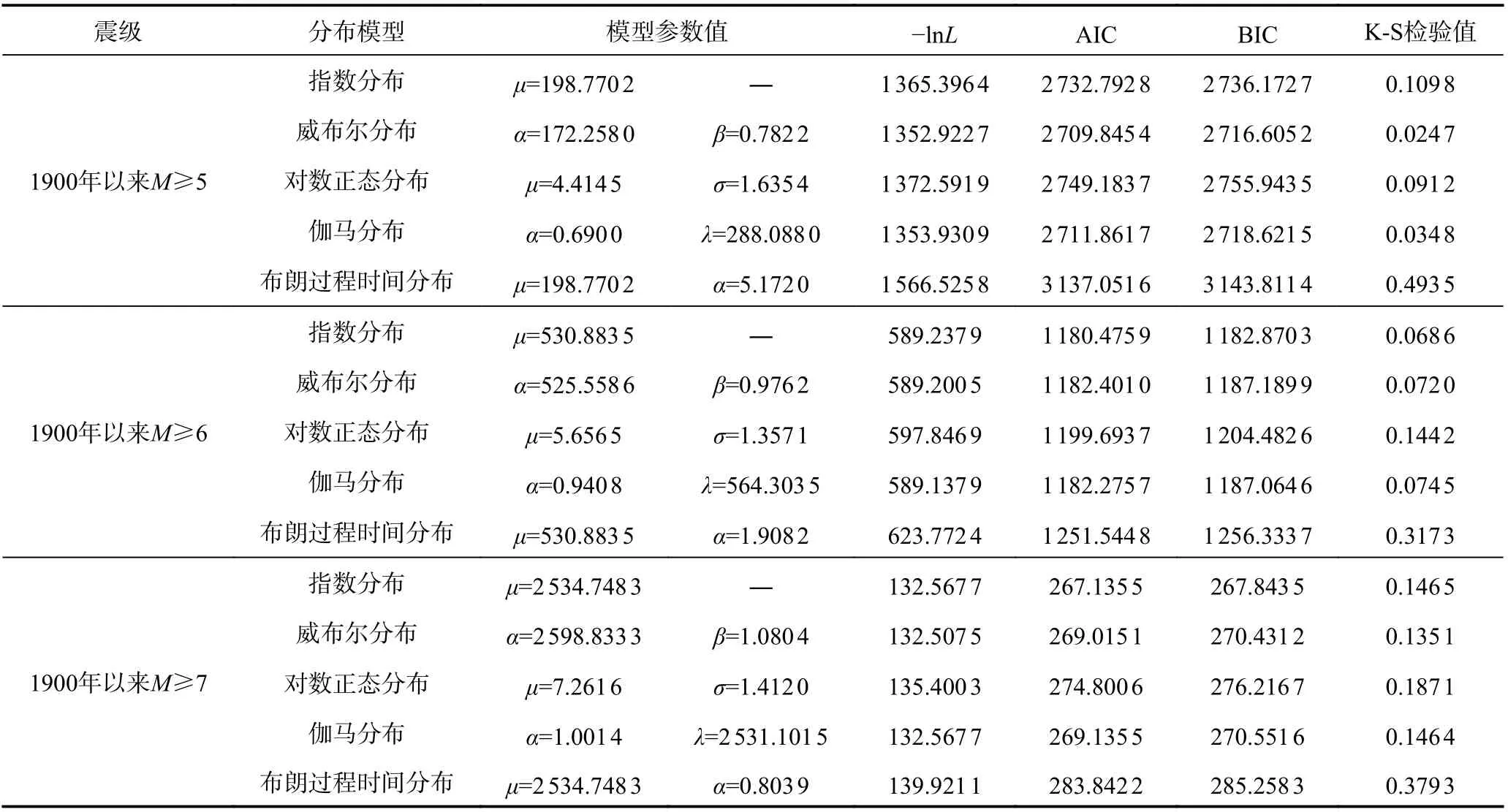
表4 台湾-马尼拉海沟地震带模型参数及AIC、BIC 和K-S 检验值Table 4 Model parameters and AIC, BIC and K-S test results for earthquakes in Taiwan - Manila trench seismic zone

本文计算了琉球海沟地震带各模型参数值和模型拟合优度判定准则参数值，得到了与上述地震带相似的结论。特别地，在琉球海沟地震带，对于M≥7 级地震，正态对数分布和布朗过程时间分布拟合优度最好。这再次说明了对数正态分布和布朗过程时间分布在描述大地震时间分布特征的方面具有优越性，同时意味着琉球海沟地震带内7 级以上地震具有一定的时间相关性。

根据上述分析可知，对于震级相对较小的地震（M＜6），指数分布、伽马分布以及威布尔分布均能较好地描述地震时间分布特征。在大的区域范围内（如整个海域），震级相对较大的地震（M＞6）可采用指数分布描述其时间分布特征。在较小的区域范围内（如地震带），大地震时间间隔可能更符合对数正态分布和布朗过程时间分布。

3 地震时间丛集性和相关性分析

地震在时间上呈现丛集现象是相对于地震在时间上是完全随机分布（指数分布）而言的，是指地震在一段时间内集中成组发生，而后在一段时间内表现出相对频度降低的特征，然后又集中成组发生的现象。地震时间丛集一直是地震学家关心的重要问题，其对地震预测和地震危险性分析具有重要影响。围绕地震在时间上是否丛集，地震学家们做了许多探索和研究，有的研究表明全球地震在时间上遵从指数分布（Michael，2011；Shearer 等，2012；Daub 等，2012；Parsons 等，2012），有的研究认为地震呈现丛集特征，但每个丛集之间相互独立（Mega 等，2003），还有的研究表明地震之间存在相互影响且呈现丛集特征（Scafetta 等，2004；Bufe，2005；Kulkarni 等，2013；Salditch，2020）。

本研究从地震时间间隔的变异系数(Coefficient of Variation)入手，采用扩散熵分析和标准差分析方法对中国海域地震时间丛集特征进行研究。

一套地震时间序列中，若存在丛集性，则在统计量上表现为地震之间的时间间隔离散性变大（相对于泊松模型），变异系数是比较2 组数据（本研究为实际观测数据和泊松模型数据）离散程度大小的理想参数，其定义为标准差与均值的比值。对于实际地震记录，连续地震之间的时间间隔是确定的，因此可以计算出1个变异系数。对于指数分布，其变异系数的理论值为1，但由于受样本量的影响，符合泊松模型的随机变量的变异系数不可能完全为1，而是呈现以1 为均值的分布。我们采用蒙特卡洛方法模拟1 000 套和实际观测数据样本相同的符合指数分布的随变量，计算每1 套模拟数据的变异系数，将其分布与实际观测数据的变异系数进行比较。图3 为整个海域M≥5、M≥6、M≥7 级地震变异系数与泊松模型变异系数的对比，可以看出在1%的置信度下，M≥5 地震被拒绝接受为指数分布的假设，其变异系数即使在1%置信度的极端情况下也大于指数分布的变异系数，这意味着M≥5 地震在时间上具有丛集性。M≥6、M≥7 级地震的变异系数在5%置信度下接受为指数分布的假设，这也意味着海域地震中主要是M5～M6 级地震体现出时间丛集性。

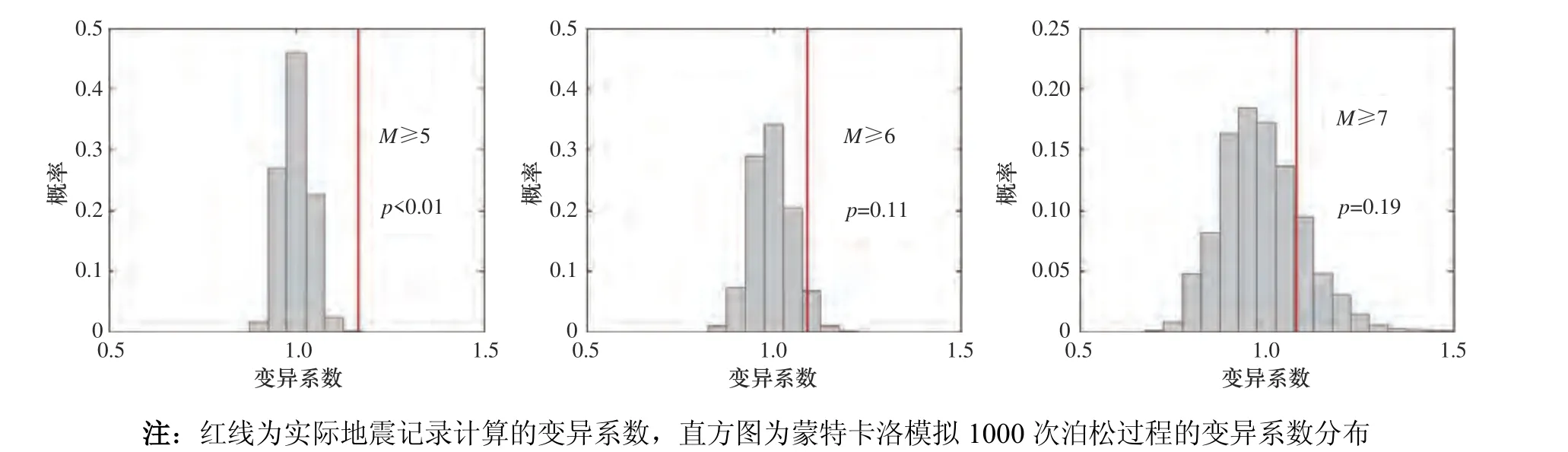
图3 海域地震时间间隔变异系数与泊松模型变异系数对比Fig. 3 Comparison between the variation coefficient of sea area earthquake time interval and the variation coefficient of Poisson model

采用扩散熵分析和标准差分析方法分析地震的时间相关性。扩散熵分析法的标度参数为δ，标准差分析法的标度参数为H（Hurst exponent）。当随机变量的δ=H=0.5 时，表示随机变量符合指数分布，变量之间无相关性，实际情况下若计算的标度值接近0.5±0.05，则认为变量无相关性；当H＞δ＞0.5 时，则认为变量之间具有相关性且具有长期记忆性，即在某一丛集期内，一次地震的发生促使下一次地震的发生；当H＜0.5 时，则认为地震之间具有负相互作用，即一次地震的发生使下次地震延迟了，在实际情况下，由于地震样本量较少，即使符合指数分布，计算的标度值偏小，这已被蒙特卡洛模拟结果证明，因此若计算的标度值小于0.5，则认为变量符合指数分布。

图4 为整个海域地震的扩散熵分析法和标准差分析法分析结果，可以看出对于M≥5 级以上地震，标度参数均大于0.5，这意味着海域5 级以上地震之间具有相关性；对于M≥6 和M≥7 地震，标度参数则非常接近0.5，表现出完全随机性，说明地震之间无相关性。这意味海域地区M5～M6 地震受更大地震（M≥6、M≥7）活动的影响，大地震发生后促使了中小地震的发生。

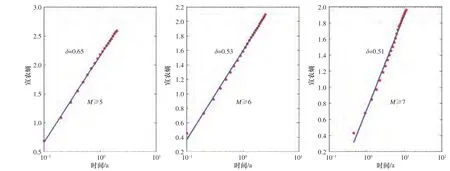
图4 整个海域地震的扩散熵和标准差随时间变化及其标度值Fig. 4 Diffusion entropy and standard deviation of earthquakes as the function of time in the whole sea area and the scale values

针对不同地震带计算不同震级地震目录的扩散熵分析法和标准差分析法标度参数（表5），对于华南沿海地震带，M≥4 级以上地震表现出时间相关性，M≥5、M≥6 级以上地震可认为符合指数分布，这说明该地震带M4～M5 级地震受M≥5、M≥6 级以上地震的影响。在长江下游-南黄海地震带，5 级以上地震表现为时间丛集，且受更大地震（M≥6 级以上）的控制。对于台湾西部地震带，M≥5、M≥6 级地震均具有时间相关性，这说明该地震带内M=5、M=6 级地震相互促进或受更大震级地震的控制。在台湾-马尼拉海沟地震带，M≥5 地震呈现出时间丛集性，M≥6、M≥7 级地震则符合指数分布，这说明了M5～M6 级地震受更大地震的影响。在琉球海沟地震带内，M≥7 级地震表现出相互促进作用，在地震预测和地震危险性分析中需要重点考虑。

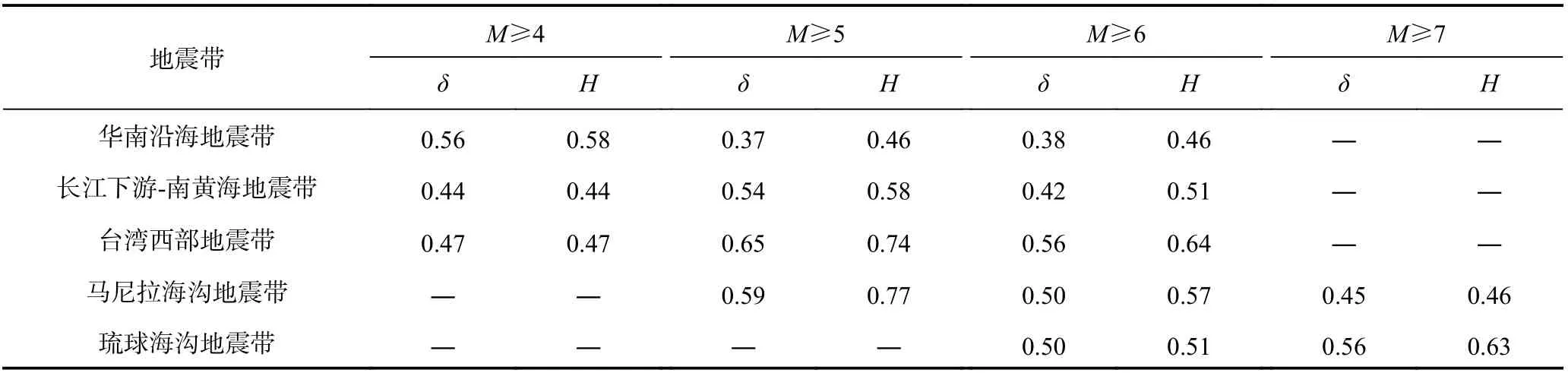
表5 各地震带不同起始震级地震目录的扩散熵分析法和标准差分析法标度值Table 5 DEA and SDA scale values of earthquake catalogs with different initial magnitudes in each seismic zone

以往的研究中，科学家们关注大地震之间的时间相关性（Bufe，2005；Michael，2011；Shearer等，2012；Daub 等，2012；Kulkarni 等，2013；Salditch，2020），本研究表明，即使在删除余震和前震后，地震目录中的大地震与中小地震之间也具有时间相关性，这意味着大地震的发生促进了中小地震的发生，使地震活动在统计特征上表现出长期记忆性，中小地震在时间轴上呈现丛集特征。

4 结论与讨论

由上述分析可知，在大的区域范围内（如整个海域区域），起始震级稍小的地震（M≤5、M≤6）时间分布多与指数分布吻合更好，威布尔分布和伽马分布的拟合优度也较好；起始震级大的地震（M≥6、M≥7）则完全符合指数分布。在一个较小区域范围内（如地震带），指数分布、威布尔分布和伽马分布均能较好描述震级较小地震的时间分布特征，对于起始震级大（M≥6、M≥7）的地震，对数正态分布和布朗过程时间分布有时具有较好的拟合优度。这与其他学者的研究结果相似（Matthews 等，2002；Bajaj 等，2019）。由于威布尔分布和伽马分布在特殊情况下可退化为指数分布，因此，在较大区域内，在遵从科学性的前提下，本着便于使用的原则，泊松模型可选择作为进行地震危险性分析的基本模型。

由于大地震发生率对于地震危险性具有重要的意义，在较小区域内（如某潜在震源区或某条断层），若历史地震目录较为丰富，可尝试采用对数正态模型或布朗过程时间模型计算高震级地震的发生概率和发生频度，这为地震危险性分析中地震发生率的计算提供了新途径，从而使地震危险性计算结果更加科学合理。目前，也有一些学者和机构采用对数正态分布模型或布朗过程时间模型来计算地震危险性（Hebden 等，2009；Working Group on California Earthquake Probabilities，2013；Petersen 等，2014），并取得了新的认识，为地震灾害的预测预防提供了重要支撑。

对海域地震时间丛集性和相关性进行分析，结果表明，在某区域内稍小震级的地震易受更大地震的影响，在时间上呈现丛集性，而震级大的地震则更多地表现出完全随机性（符合指数分布）。一方面这是由于目前没有有效的方法区分主震和余震，即使删除余震，地震目录中仍然包含数量相当的余震（中小震）。另一方面，在大地震发生后，应力扩散和调整需要较长时间，表现为中小震级地震的发生（Shearer 等，2012），在统计特征上表现为丛集性和长期记忆性（即H＞0.5），因此，在对某地区进行地震危险性分析时应充分考虑该地区最近一次发生的强震对未来中小地震的影响。本研究还发现在地震活动非常强烈的琉球海沟地震带，M≥7 级地震表现出正向的相关性，即某次7 级以上地震的发生会促使下次7 级以上地震的发生，需要引起特别注意，这一发现对于理解地震孕育发生机理具有一定科学意义。