黄土场地地铁车站振动台试验方案设计与研究1

王玉铃 权登州 柴少波 卜永红 王毅红

（长安大学，建筑工程学院，西安 710061）

引言

黄土场地在中强地震作用下易发生震陷、滑坡、液化和地震动显著放大等，会诱发和加重工程结构地震灾害，在黄土场地修建地铁存在较高的地震破坏风险（王兰民等，2014）。多位学者针对黄土场地及其工程动力响应开展了研究（权登州等，2015），如慕焕东等（2014）基于试验研究，建立了地裂缝带黄土等效黏弹性动力本构模型；张希栋等（2015）通过试验研究，揭示了双向动荷载作用下黄土动剪切模量随动剪应变的变化规律；陈拓等（2017）利用等效线性化波动分析法，定量研究了土质和厚度对黄土场地地震动效应的影响；夏坤等（2018）分析了汶川地震远震区黄土场地地震响应特征，发现黄土场地地面峰值加速度较大，反应谱平台范围较宽；王谦等（2019）研究了饱和黄土动力特性区域差异性，发现区域分布对饱和黄土动剪切模量比的影响较小，对阻尼比的影响显著；高中南等（2019）通过试验研究验证了掺入粉煤灰可有效改善饱和黄土地基抗震性能；韩建平等（2020）开展了黄土场地地下1 层、地上2 层地铁车站结构抗震性能研究，发现地上、地下结构交接处破坏最严重。然而，针对黄土场地地铁车站地震响应的研究仍较薄弱，对破坏机理缺乏足够的认识。因此，有必要通过大型地震模拟振动台模型试验揭示黄土场地地铁车站地震响应特性及规律。

本文选取黄土台塬区典型2 层双跨地铁车站-西安地铁4号线飞天路车站为原型结构，研究振动台试验相似设计原则、模型材料选择与模型制作技术、传感器优化布置与地震动输入等，对振动台试验方案进行详细说明。通过振动台试验，得到模型体系地震响应数据与震害分布特征，对比分析结果表明，模型结构宏观震害与数值模拟结果较吻合。

1 模型相似设计

目前，模型结构动力试验中的相似关系包括弹性相似律、重力相似律和弹性-重力相似律。在考虑土与结构动力相互作用的地震模拟振动台模型试验中，使模型体系与原型完全满足相似关系十分困难，在现有条件下往往无法实现，需根据动力问题特点确定试验中的相似关系（李振宝等，2010）。本试验主要研究黄土场地与地铁车站动力相互作用体系地震响应及破坏分布，据此可确定振动台模型试验相似设计原则如下：

（1）由于地铁车站模型尺寸较小，采用附加全配重的人工质量模型消除重力失真效应难以实现，因此，本试验采用欠人工质量模型；

（2）应考虑多介质耦合效应，因此，地基土与地铁车站结构相似关系应尽量保持一致；

（3）本试验模拟地震动作用下地基发生大变形及结构临近破坏的特性，模型材料应力-应变关系和模型结构抗力应尽量与原型相似，且模型材料性能应稳定、易于加工；

（4）应充分考虑试验设备尺寸、动力性能、承载吨位及配套元器件性能等。

按照上述原则，选取长度、弹性模量及加速度为基本物理量，并根据Bockingham 的π 定理确定模型体系相似关系，如表1 所示。由表1 可知，模型结构密度相似常数为3.0，而模型结构材料微粒混凝土密度与原型结构混凝土密度接近，因此，需附加人工质量以满足模型结构密度相似要求。本试验采用在模型结构中均匀粘贴铅块的方法实现附加人工质量，从而可充分考虑模型结构惯性力作用。

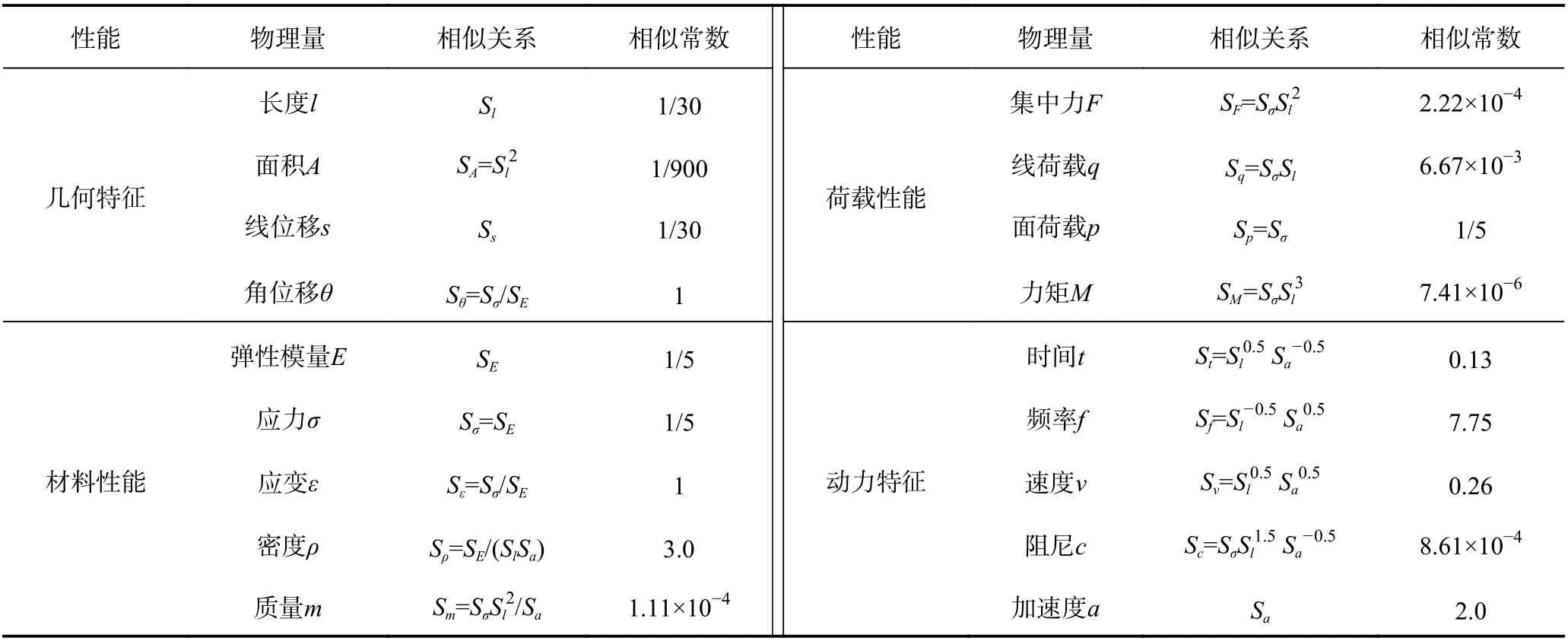
表1 模型相似常数Table 1 Similar constants of test model

2 模型结构制作

2.1 模型材料

本试验采用微粒混凝土模拟普通混凝土，为获得满足相似关系的低弹性模量微粒混凝土，使用石英砂和具有连续级配的河砂分别模拟普通混凝土中的粗骨料与细骨料，通过室内试验研究用水量、石灰掺量和粗骨料掺量对微粒混凝土受压性能的影响。在不同配合比下，采用微粒混凝土制作6 个边长70.7 mm 立方体试块和6 个100 mm×100 mm×300 mm（长×宽×高）棱柱体试块。将立方体试块分成2 组，分别测试7 d 和28 d 立方体抗压强度。将棱柱体试块分成2 组，分别测试28 d 轴心抗压强度和弹性模量，试验结果如图1 所示。

图1 微粒混凝土弹性模量和抗压强度Fig. 1 Elastic modulus and compressive strength of microconcrete

分析试验结果可得以下结论：

(1)随着用水量的增加，微粒混凝土中孔隙结构增多，使试块弹性模量、立方体抗压强度和轴心抗压强度均明显降低；随着粗骨料掺量的增加，粗骨料刚性骨架作用与试块破坏时需克服粗骨料从基材中拔出的摩擦作用增强，微粒混凝土弹性模量、立方体抗压强度和轴心抗压强度均增大。

(2)掺入石灰后，微粒混凝土抗压强度和弹性模量均显著提高，且抗压强度提高幅度大于弹性模量；随着石灰掺量的增加，试块立方体抗压强度逐渐增大，轴心抗压强度与弹性模量先增加后减小。

(3)通过增加用水量或减小粗骨料掺量，可降低微粒混凝土弹性模量和抗压强度。改变石灰掺量，可通过不同变化率调整微粒混凝土弹性模量与抗压强度。

基于力学性能试验研究结果与室内试配试验，确定微粒混凝土配合比为水泥∶细料∶粗料∶石灰∶水=1.0∶6.5∶0.5∶0.5∶1.4，测得该配合比下微粒混凝土棱柱体抗压强度为8.11 MPa，弹性模量为6 602 MPa，可满足本试验模型结构材料相似要求。

2.2 制作工艺

采用微粒混凝土和镀锌钢丝制作地铁车站模型，根据原型结构与相似关系确定模型结构尺寸，按照原型与模型相应构件间弯矩、剪力等效，并考虑施工可操作性，确定模型结构钢筋布置。

模型结构板与侧墙采用钢丝网双向配筋；纵梁与中柱布置钢筋骨架，其中主筋与箍筋通过焊接连接；板与侧墙、纵梁结合部设置腋角，腋角钢筋采用绑扎方式与相邻构件钢筋连接。制作模型结构所用模具分为外模和内模，外模采用木板，并按照模型结构外轮廓尺寸制作，形成浇筑模型结构的外围边界；内模分上下2 层，制作内模时，按每层模型结构内部最大净高、净宽及纵向长度，采用聚苯乙烯塑料泡沫制成长方体，并在其上挖除模型结构内部构件占用的塑料泡沫，形成中柱、纵梁及腋角等内部构件浇筑空间。制作完成的外模和内模如图2（a）所示。

模型结构制作过程为：①找平场地并将外模固定；②将模型结构底板与侧墙钢筋网分别放置于外模底部和侧边，并浇筑底板微粒混凝土；③待底板表面水分稍干后，放置下层聚苯乙烯塑料泡沫内模，同时将中柱、纵梁及腋角钢筋骨架置于下层内模预留浇筑空间内，将中板钢筋网铺设于下层内模上方中板所在位置；④同时浇筑模型结构下层侧墙、中柱、纵梁、腋角及中板微粒混凝土，并采用微型振捣工具与人工振捣相结合的方式将混凝土振捣密实；⑤待中板表面水分稍干后，按照相同施工工艺，放置上层内模及钢筋，并浇筑模型结构上层构件，制作并养护完成的模型结构如图2（b）所示。

图2 模型制作Fig. 2 Manufacturing model

3 模型地基制作

地下结构振动台试验中，模型土箱模拟效果对试验结果的影响较大。本试验采用叠层剪切模型土箱，净尺寸为3.5 m×2.0 m×1.7 m（振动方向×纵向×竖向），采用15 层方钢管框架叠置并辅以双侧面钢板约束的方案，每层框架由4 根截面尺寸为100 mm×100 mm、壁厚为3 mm 的方钢管焊接而成，层间沿水平振动方向设置V 形凹槽，并在其内放置钢滚珠，以形成可自由滑动的支承点。模型土箱内壁设置2 mm 厚橡胶模，以防止土样和水漏出，其底部与振动台台面通过螺栓固定，如图2（c）所示。该模型土箱可模拟自由场地边界条件，较理想地消除边界地震波反射或散射效应（陈国兴等，2010）。

为反映黄土场地特性，尽量使模型地基与原型场地条件相似，制作模型地基的黄土取自飞天路车站施工基坑，所取土样位于地表以下6～8m，呈褐黄色，大孔且虫孔发育，可见少量白色钙质条纹及蜗牛壳碎片，以硬塑状态为主，局部呈可塑状态，土样物理指标如表2 所示。制作模型地基时，按黄土天然含水量和密度控制模型地基含水量及密度，将黄土试样分层装入模型土箱并进行压实，装入每层土样前对下层土体表面进行拉毛处理。土样装填至模型结构底面高度处，将模型结构吊送至模型土箱内并进行定位。在模型结构中粘贴附加人工质量块后采用软质塑料板对端部进行封堵，继续装填土样至模型地基表面。装填土样时将传感器数据线沿水平方向引至模型土箱侧板，集中封装后紧贴侧板沿竖向由模型地基内引出，避免振动过程中数据线损坏失效。

表2 土样的物理指标Table 2 Physical parameters of soil samples

4 数值模拟分析

4.1 模型建立

飞天路车站宽19.2 m，高14.01 m，上覆土层厚3 m，顶板、中板及底板厚度分别为0.8、0.4、1.0 m，侧墙厚0.7 m，中柱为1.2 m×0.8 m 矩形断面，中柱间距为9.0 m，在板与侧墙、纵梁结合处进行加腋处理。

利用ABAQUS 软件建模，采用有限元-无限元耦合的方法，通过有限元模拟车站结构及近场黄土，通过无限元传输边界模拟远场黄土（Lysmer 等，1969；Chen 等，2015），如图3 所示。黄土场地尺寸取150 m×70 m，土层组成与力学参数如表3 所示，黄土材料特性采用Davidenkov 本构模型描述，动剪切模量比Gd/Gmax及阻尼比λ随剪应变的变化关系如图4 所示。近场黄土采用四边形平面应变缩减积分单元CPE4R 模拟，远场黄土采用四边形平面应变无限单元CINPE4 模拟。车站结构按实际尺寸建模，采用四边形平面应变单元CPE4 模拟，混凝土材料特性采用塑性损伤模型CDP 模拟（孙海峰，2011），密度取2 500 kg/m3，杨氏模量取2.1×1010Pa，泊松比取0.2。黄土场地与地铁车站动力相互作用采用主从接触面模拟（费康等，2017），对于法向接触，以罚函数模拟界面闭合与分离机制，对于切向接触，采用弹性滑移变形模拟界面摩擦与滑移机制。根据原型场地条件，采用Geostatic 模块计算初始地应力，使用生死单元功能模拟地铁车站施工过程，获取施工完成的地应力场，作为动力分析步初始应力状态。输入地震动采用重现期为475 年的西安人工波，峰值加速度为200.6 cm/s2，强震持时为60 s。

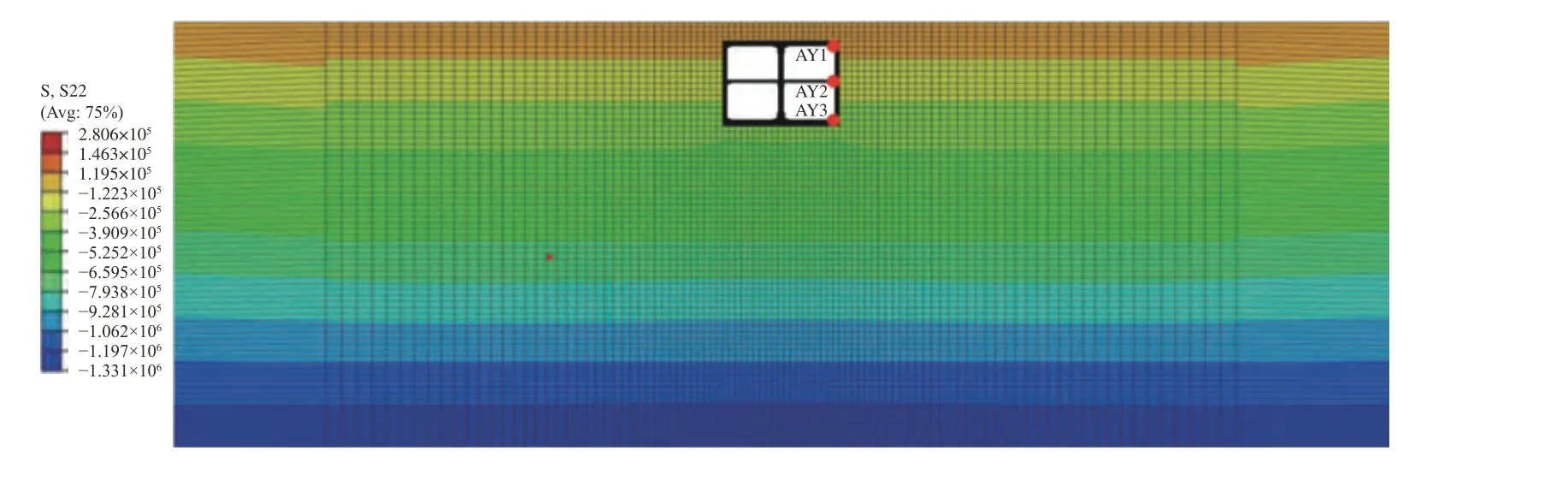
图3 有限元-无限元耦合分析模型Fig. 3 Analysis model of finite-infinite element method

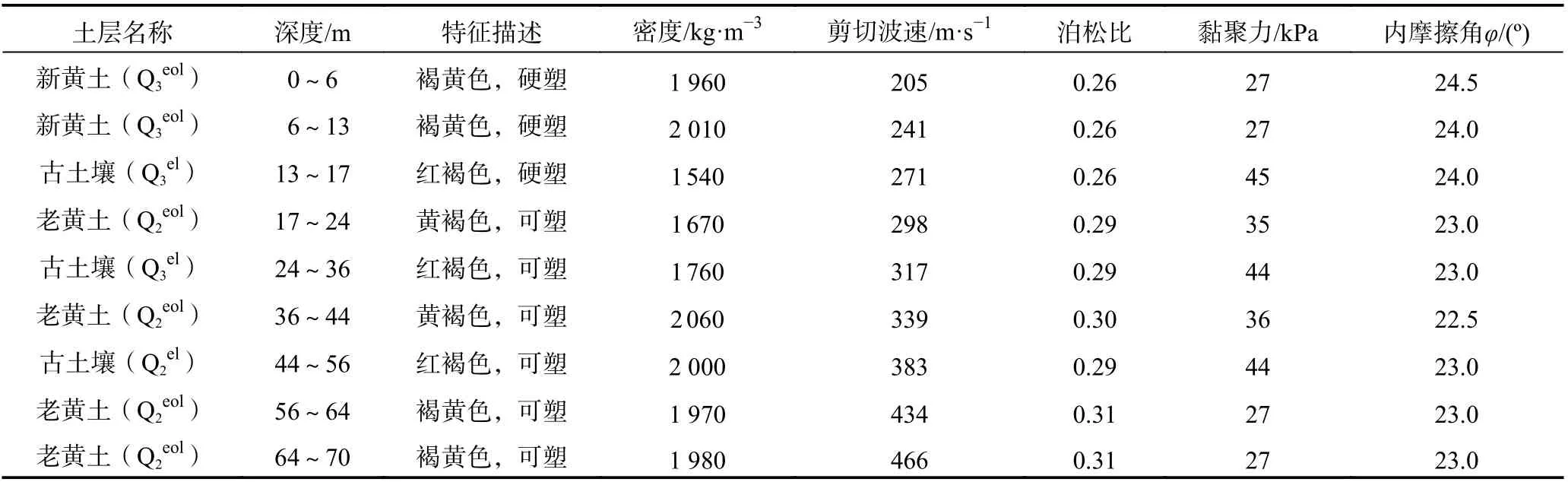
表3 黄土场地土层组成与力学参数Table 3 Soil composition and mechanics parameters of loess site

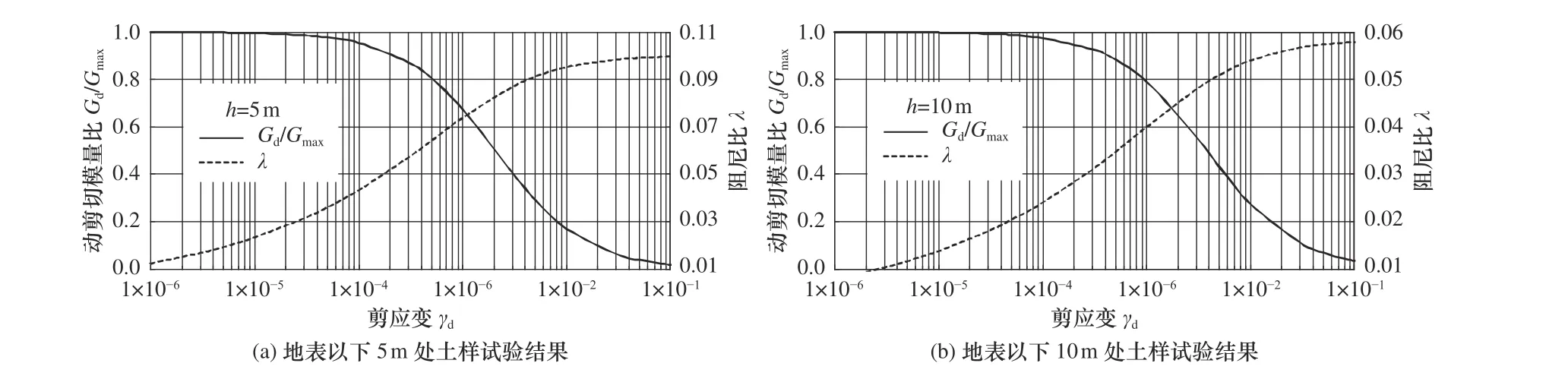
图4 黄土动力特性试验结果Fig. 4 Dynamic characteristics of loess

4.2 地铁车站地震响应

黄土场地地铁车站地震响应数值模拟结果如图5 所示，由图5（a）可知，地震作用结束后地铁车站发生了损伤，上层柱顶与下层柱底损伤最严重，呈现连通的受拉损伤区域，宽度达中柱截面宽度的2/3；侧墙内部与顶、底板连接处损伤较重，受拉裂缝发育较深；板构件损伤较轻，仅在较小范围内产生了微小受拉裂缝。由图5（b）可知，中柱顶部及底部应力较大，侧墙内部与板构件连接处应力较大，板构件内部与侧墙、中柱连接处应力较大，侧墙及板构件中部应力较小。由图5（c）可知，地基顶、底部发生最大剪切变形时，内部各测点水平相对位移随土层深度的减小逐渐增大。

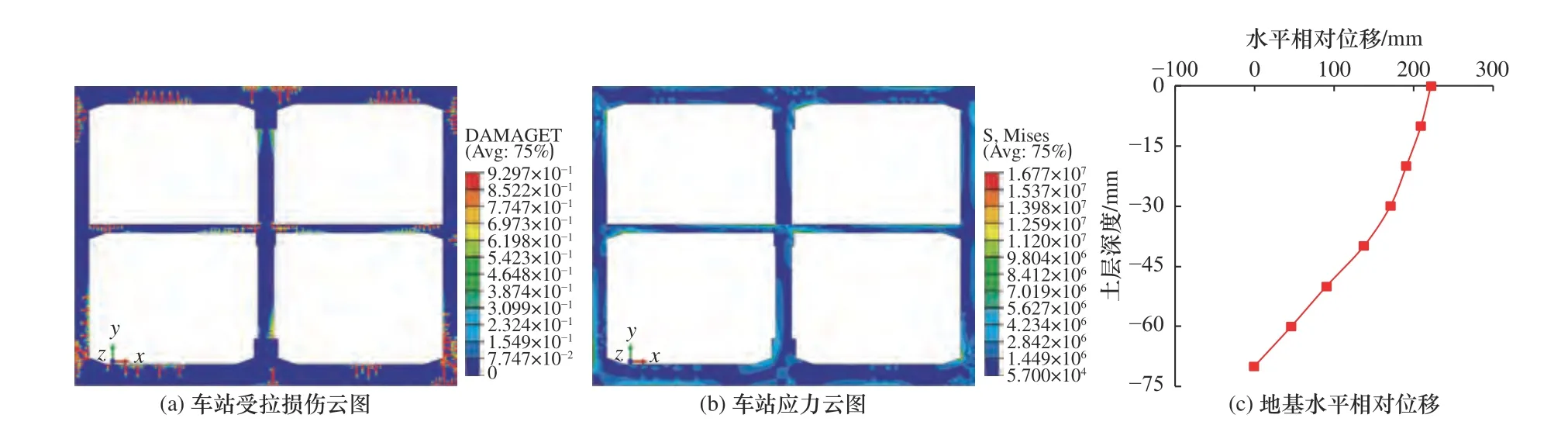
图5 黄土场地地铁车站地震响应数值模拟结果Fig. 5 Numerical analysis results of subway station in loess

5 传感器布置

5.1 布置原则

在激振过程中主要测试模型地基加速度、水平位移和竖向沉降，模型结构加速度与应变反应及黄土场地与地铁车站相互作用界面接触土压力等，数据采集传感器如图6 所示，根据数值模拟结果及试验条件，确定本试验传感器布置原则如下（韩俊艳等，2018）：

图6 数据采集传感器Fig. 6 Sensors of shaking table test

（1）主观测断面应选取与中柱轴线重合的横断面，使测量数据尽量符合二维平面应变假设。

（2）模型结构主观测断面与结构端部的距离应大于结构横向宽度，以减弱端部效应对主观测断面动力响应的影响。

（3）横向观测断面数量不少于2 个，其中主观测断面1 个，其余为次观测断面，主观测断面传感器数量多于次观测断面。在主观测断面中柱及其他关键部位两侧布置应变片，以对构件两侧受力、变形进行对比分析；在与主观测断面相同的关键部位设置次观测断面传感器，可相互验证数据的可靠性；在模型结构纵向端部附近设置少量传感器，以研究端部效应对模型结构受力、变形的影响。

（4）模型结构关键部位同时布置多个传感器，应协调传感器相对位置，保证互不干扰。

（5）本试验共设88 个数据采集通道，应充分利用各通道，对尽量多的关键部位进行测量，以全面采集模型体系地震响应。

5.2 布置方案

根据传感器布置原则，共设6 个横向观测断面，如图7（a）所示，包括1 个主观测断面和5 个次观测断面。其中主观测断面和1～3 号次观测断面位于通过模型结构中柱轴线的横断面，主要采集车站结构及周围黄土地震动力响应；0、4 号次观测断面设在通过模型结构端部的横断面，用于研究模型结构纵向端部效应对结构中部地震响应的影响。传感器布置如图7（b）、7（c）所示，加速度传感器A1～A19 用于采集主观测断面模型地基与结构加速度响应，加速度传感器A20～A22 设在2 号次观测断面与传感器A3～A5 对应的位置；加速度传感器A23、A24 分别设在3、4 号次观测断面中与传感器A5 对应的位置；加速度传感器A25设在模型底座，用于检验台面输入地震波精度；加速度传感器A26 设在0 号次观测断面与传感器A19 对应的位置，用于研究垂直于振动方向上模型地基边界效应。共设44 个应变片，编号为S1～S44，主观测断面设置28 个（编号为S1～S28）；共设7 个土压力传感器，编号为P1～P7，主观测断面设置5 个（编号为P1～P5），用于采集黄土场地与地铁车站动力相互作用接触压力；共设5 个位移传感器，编号为L1～L5，用于量测模型地基水平位移；共设2 个激光位移计，编号为G1、G2，用于测量模型体系竖向沉降。

图7 观测断面位置与传感器布置示意Fig. 7 Arrangement plan of sensors for shaking table test

6 试验加载方案与震害分析

6.1 试验加载方案

本试验采用美国MTS 公司生产的水平单向高性能地震模拟振动台，台面尺寸为3.36 m×4.86 m，最大载重量为25 t，工作频段为0.1～50 Hz，振动波形可为随机波及各种地震波，满载最大加速度为±1.0g，最大速度为±500 mm/s，最大位移为±120 mm，最大倾覆力矩为45 t·m。为研究不同地震动特性的影响，分别选择Taft 波、松潘波和西安人工波作为输入地震动，地震动加速度时程与反应谱如图8 所示。

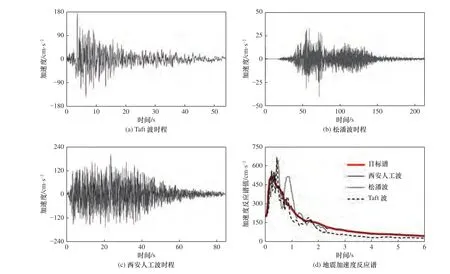
图8 输入地震动加速度时程与反应谱Fig. 8 Time-histories and Fourier spectra of input accelerations

振动台试验是损伤累积过程，地震动输入需遵循激励机构反应由小到大的顺序。对于同级荷载，地震动输入顺序按以下方法确定：计算体系参与质量大于50%对应的主要周期点，对选定的各地震波在主要周期点处各方向上的反应谱加权求和，按该值从小到大的顺序确定地震动输入顺序（周颖等，2012）。本试验加载工况如表4 所示，各工况开始和结束时均需输入白噪声。

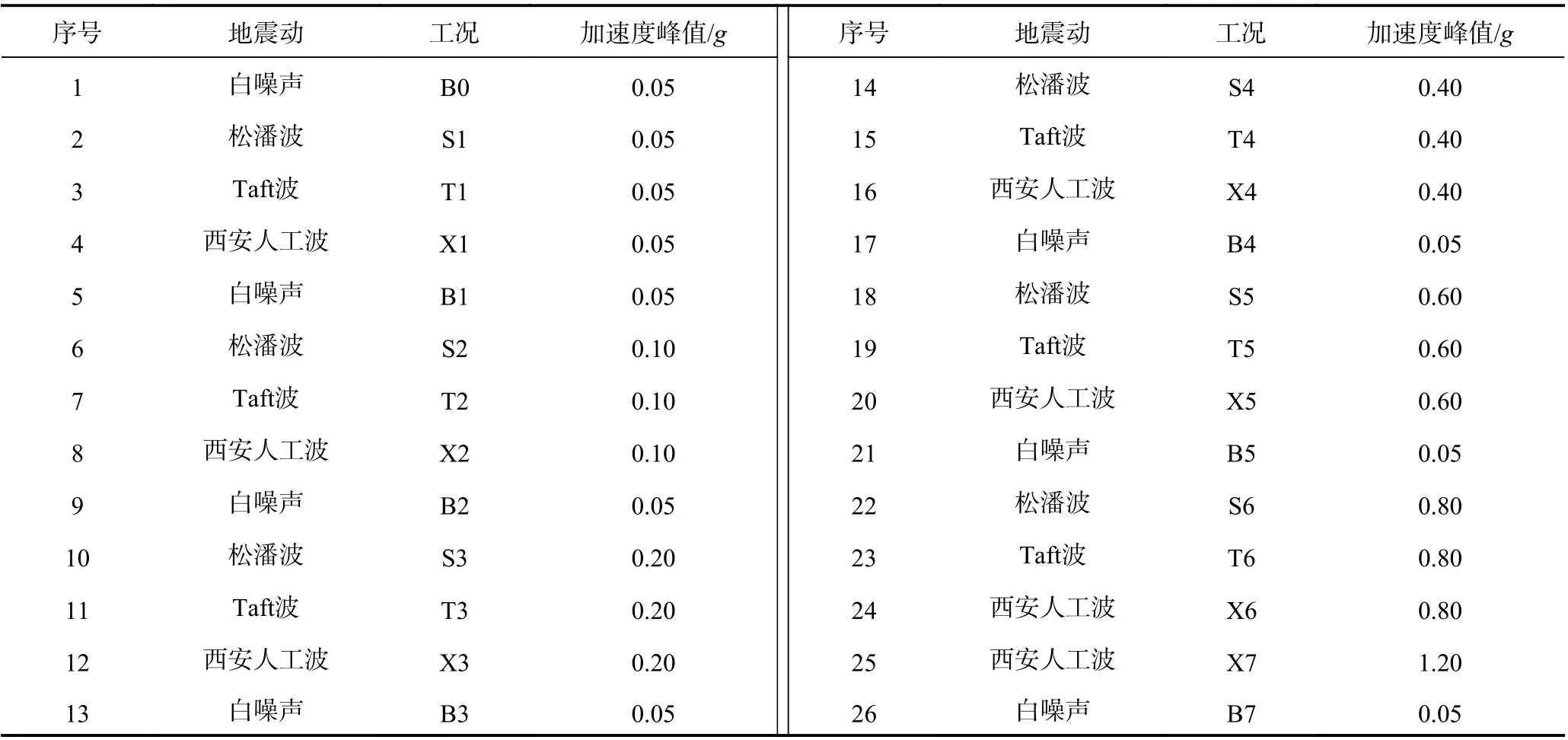
表4 试验加载工况Table 4 Loading conditions for shaking table test

6.2 地震破坏分析

振动台试验结束后，模型地基表面沿结构四周出现连通的环状主裂缝，以主裂缝为源头出现数条支裂缝，并向远离结构的方向蔓延，且主裂缝两侧土体出现沉降差，如图9（a）所示。将模型结构挖出观察其破坏情况，如图9（b）～9（d）所示。模型结构上层中柱出现典型剪压破坏，产生严重的竖向裂缝；下层中柱微粒混凝土大量剥落，纵向受力钢筋外露；上层中柱与顶板连接处及下层中柱与底板连接处破坏最严重；侧墙内部与底、顶板连接处产生裂缝，局部腋角钢筋从微粒混凝土基材中拔出。模型结构内部采集的视频资料显示，X6 工况下，仅在中柱与顶、底板连接处产生了裂缝；X7 工况下，结构破坏严重，呈现出最终的破坏状态。对比图9（b）～9（d）和图5（a）可知，振动台试验得到的模型结构破坏特征与数值模拟分析得到的地铁车站损伤分布较吻合。因此，本文设计的振动台试验较可靠。

图9 模型体系地震破坏情况Fig. 9 Seismic damage of test model

7 结语

本文以实际工程为背景，对黄土场地典型2 层双跨地铁车站大型地震模拟振动台试验方案进行设计与研究，得出以下结论：

（1）提出了黄土场地与地铁车站动力相互作用振动台试验相似设计原则，基于Bockingham 的π 定理，对振动台试验中采用的欠人工质量模型进行相似设计，并在模型结构中粘贴铅块以实现附加人工质量。

（2）通过室内力学性能试验研究，得到满足振动台试验相似条件的微粒混凝土配合比，确定合理的模型结构制作材料。选取施工基坑黄土制作模型地基，并给出模型地基详细制作方案，为黄土场地地下结构振动台试验模型设计与制作提供参考。

（3）采用有限元-无限元耦合的建模方法，分析黄土场地地铁车站地震响应，并基于数值模拟结果进行振动台试验传感器布置。根据典型黄土场地特性及周边地区地震环境，确定输入地震动与加载方案。

（4）震害分析表明，振动台试验得到的模型结构宏观震害与数值模拟分析得到的地铁车站损伤分布较吻合，研究结果可为黄土场地地铁车站、地铁隧道及地下商业街等地下结构大型地震模拟振动台试验方案设计与抗震研究提供参考。