基于弗洛伊得算法的云端文件存储负载平衡算法研究
陈 园,刘军华,雷超阳
(湖南邮电职业技术学院 互联网工程系,湖南 长沙 410015)
基于弗洛伊得算法的云端文件存储负载平衡算法研究
陈 园,刘军华,雷超阳
(湖南邮电职业技术学院 互联网工程系,湖南 长沙 410015)
文章提出了基于弗洛伊得算法的云端文件储存负载平衡算法,依据客户端对文件的存取频率与文件大小,综合最短网络距离的计算来优选文件存放位置,且依据所有客户端与所有服务节点间的跳跃计数与网络频宽视作其网络距离。仿真实验表明:本文研究方法其文件平均存取成本较随机与轮转两种方法明显要低,对所有使用者公平存放文件位置,让使用者能以最少的跳转次数或最佳的频宽路径进行存取,提升了客户端文件存取效率。且当多数丛集空间满载时本研究方法仍可计算出较佳的存放位置。
弗洛伊得算法;云端文件;负载平衡;算法
0 引言
随着云计算相关技术的普及以及用云技术应用的越来越广泛,如将不同云文件合理存放于不同云服务器,以满足大量用户快速存取、高吞吐量及大储存空间需求。因而,怎样合理安排文件的云存放位置,使客户端获取时响应时间较短非常重要。通常的思路是每隔一段时间周期性的收集云端系统内文件的存取需求作为负载平衡的依据,依此分析当前时间段文件的合适存放位置,即通过周期性的收集与分析云系统信息使近阶段文件的存放位置接近最佳化[1-5]。而判断文件存放的位置考虑因素既可以是存放在较空闲服务器来降低客户端的等待时间,也可以是存放在距离客户端较近的位置来降低传输成本[6-8]。
本文提出的弗洛伊得算法的云端文件存储负载平衡算法,以弗洛伊得算法计算出客户端至所有服务节点的最短网络路径,同时考虑不同客户端对同文件存取需求,不只将文件存放在离单一客户端最近位置,即不同客户端存取文件次数及大小也是考虑要素。对于较大文件即使被存取次数较少,也要考虑将其存放在较近位置,以避免存取该文件的客户端因传输所需文件而造成较大延迟。而对于存取次数较多但较小文件,即使存放在离其较远位置也不至于造成太大延迟。且当计算出适合存放的服务节点满载时,通过设计好的满载文件迁移规则,使服务节点中的文件迁移调整后对客户端造成的影响最低。
1 弗洛伊得算法思路
弗洛伊得算法(Floyd)是一种在有向加权圆中寻找任意两点间最短路径的算法[9-12]。其思路是如果一个问题存在最佳解则其子问题必有最佳解,将有向加权圆中的任意两点间所有可经过点间最短距离作为子问题,先分别解出各子问题最佳解,最后将子问题解进行最佳组合从而得到问题的最佳解。其算法描述为:设Di,j,k为某图从点i到点j经由(1~k)集合点为中间节点的路径长度为子问题,则子问题可分两种情况。
(1)经过中间k节点的路径距离Di,j,k=Di,k,k-1+
(2)不经过中间k节点的路径距离Di,j,k=Di,j,k-1
这样子问题最短路径变为:Di,j,k= min(Di,k,k-1+Dk,j,k-1, Di,j,k-1),即取经过中间k节点路径距离与不经过中间k节点路径距离(即直接相连节点)两者的较小值。若经过中间节点距离较短,则以此距离取代原本两点直连的距离,依此不断的比较与取代将加权圆中任意两节点间的最短路径距离计算出来。
2 网络距离计算
网络距离通常是计算云端文件储存位置的主要评估要素,其计算方式是以客户端入口点与文件服务器丛集之间的跳跃计数及频宽来计算,如图1所示。

图1 服务器丛集与入口点连线频宽示意图Fig.1 Bandwidth map of the server cluster and the entry point
图1中没带箭头线段上的数字表示丛集间的频宽,带箭头线段上的数字表示入口点到直连丛集间的频宽,入口点到丛集为有向,丛集间为无向且互相连通,但不一定直连。取频宽的倒数来表示丛集间的相连传输延迟(即时间距离),频宽数值与时间距离成反比,以下公式1为点x到点y的时间距离计算方法。

由图1计算出的时间距离结果如表1所示。

表1 服务器丛集直接相连网络距离表Tab.1 Network distance table of server cluster directly connected
可知有些丛集间无直接连接,需经其他丛集转连,此转连所经过的丛集数即为跳跃计数。此跳跃路径不一定为唯一路径,有时直连的距离较近,有时经由别的丛集路径较近,且选择频宽总和最小跳跃路径,这时需根据弗洛伊得算法寻找任意两点最短路径的特性,以丛集为点计算出任意两点的最短路径,计算结果为两点间跳跃计数的时间距离综合。最短距离计算方法如公式(2)。

公式2中j为两点间可经过的点集合。将频宽倒数的时间距离计算方法套用到弗洛伊得算法中,最短距离为直接相连时间距离与有经由中间点时间距离的较小值。表1加上入口时间距离后通过公式2计算的结果如表2所示。

表2 弗洛伊得算法计算网络距离表Tab.2 Floyd algorithm to compute the network distance table
由表 2可知,入口点 P1与丛集 SA、SB的连接速度较快,而入口点 P2与丛集 SC、SD的连接速度较快。但当需确定文件存放至哪个丛集时不能仅以连接速度来评估,因如果有两个入口点都要存取同一文件,如将文件存放在离入口点P1较近丛集SB,则会对入口点P2造成较远网络距离存取。所以需考虑多方面因素来计算每个入口点的存取成本,以便将文件存放在更合适的丛集。
3 文件存取成本计算
文件存取成本的计算需针对单独文件分别计算,考虑的要素有距离、各入口点文件存取次数及文件大小。通过计算各入口点对某文件的需求量,从而分别计算出每个丛集存放此文件对所有入口点造成的影响。
以下以文件f的存取成本来说明其计算步骤。
(1)先分别计算每入口点对文件f的存取需求量 ATp,f×FSf;
(2)再乘以该入口点至丛集距离 ATp,f×FSf×Dp,S;
此计算结果为单一入口点由丛集 S存取文件 f所需成本,将所有入口点的存取成本求和得TACs,f,求和计算公式3如下。
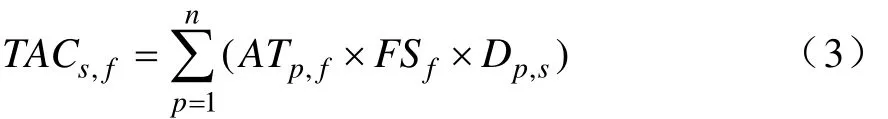
TACS,f表示所有入口点 p从丛集 S存取文件 f的成本总和。公式(3)中各代号含义如下:
P:入口点(Portal),p=1…n
S:服务器丛集(Server Cluster),S=1…m
ATp,f:文件 f从入口点 p的存取次数(Access Times)
FSf:文件f的大小(File Size)
Dp,s:入口点p到丛集s的距离
TACs,f:所有入口点由存取丛集s中文件f的总存取成本
将此公式代入不同丛集 s的距离,就能计算出文件f存放到不同丛集对应的TACs,f值,TACs,f值越小表示文件f越适合存放于丛集s。计算TACs,f值目的在于得到存取需求量与各入口点跟丛集的距离关系,计算存取文件所需成本,依照各入口点存取成本来比较,使每个入口点公平,避免只针对单一存取成本较低的入口点文件来决定最佳存放位置。即使每个文件都计算出最小 TACs,f值决定文件的存放丛集,仍可能出现多个文件存放于同一丛集情况,而丛集空间有限,这就涉及到将部分文件迁移到其他服务器的处理。
4 文件存放策略
本文所研究的文件存放策略是让每个丛集分别对所有文件中进行挑选。其挑选方式为:选出所有存放于某丛集时存取成本最低的文件。如果丛集挑选的文件大小总和超出了其储存空间,则从所有存放于该丛集的文件中选出一个移至别的服务器,直到空间足够。本算法的中止条件为所有文件都确定存放的丛集不再变动。由存取成本计算后可得到每个文件在不同丛集的存取成本,假设为TAC,并将TAC数值以矩阵编排,如表3案例所示,其中横排表示丛集编号,纵排表示文件编号,中间数值表示如文件存放在此丛集时的TAC值。

表3 文件存放成本矩阵案例Tab.3 Study of file storage cost matrix
接着先将TAC矩阵转换成相对成本矩阵,因每个文件的TAC值都是针对个别情况计算出来的,文件间的TAC值无法相互比较,所以丛集无法以TAC值确定哪个文件更适合保留。这时只能根据文件被移至别的丛集时分别增加了多少TAC值,即相对成本,相对成本计算程序如下:
Compute-relative-cost()
for i=1 to m
for j=1 to n
Ri,j=TACi,j—min{TACk,j|k=1-m, TACk,j> 0}
相对成本算法程序
以上相对成本算法程序中 i表示服务器丛集编号 1~m,j表示文件编号 1~n,Ri,j表示文件存放于丛集i的相对成本。每个文件都将其对应TAC数值减去最小TAC值,以表3案例中的文件f1为例,其最小TAC值为2,将其对应TAC值减去2,其他文件依此类推,结果如表4所示。
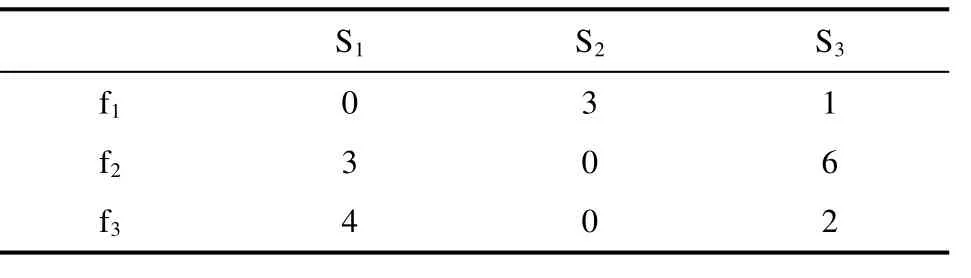
表4 相对成本计算结果案例Tab.4 Relative cost calculation case
由表4可看出最佳丛集为TAC增长为 0的丛集,当需选择移至别的丛集文件时就可选择TAC增长较少的文件。依照相对成本矩阵,丛集进行本身文件筛选,其文件筛选算法程序如下:
Main
-function()
for j =1 to n
FStatusj=false
While(∃false∈{FStatusj| j=1~n})
Compute-relative-cost()
for i=1 to m
if(Spi>0)
For j=1 to n
if(Ri,j=0 and FStatusj=false)
add j in FileListi
Spi=Spi-Fsj
FStatusj=true
end for
end for
for i=1 to m
if(Spi<0)
File-Transfer(i)
end
文件筛选算法程序
以上文件筛选算法程序中,FStatusj表示文件 j是否已决定存放位置的状态,FileListi表示服务器丛集i的文件存放列表,Spi表示服务器丛集i的剩余空间,Fsj表示文件j的大小。依据相对成本矩阵,丛集分别挑选出成本为0且还没决定存放位置的文件,并将丛集空间扣除文件大小,最后每个丛集检查其剩余空间是否为负值,如果是则表示此丛集空间不足,需要将部分文件移至别的丛集存放。将文件移出的相对成本比较算法程序如下:
File-Site(i)
for each filejin FileListi
MoveCostj=min{Ri,j|i=1~n,Ri,j>0
While(Spi<0)
j=min{MoveCostj}
Delete j from FileListi
Spi=Spi+ Fsj
FStatusj=false
Ri,j= —1
delete j from{MoveCostj}
end
服务器丛集满载文件移动算法程序
上述服务器丛集满载文件移动算法程序中,File-Transfer(i)表示服务器丛集i的文件移动设置,MoveCostj表示文件编号j的移出成本。
相对成本矩阵表示文件被移至其他丛集时其增加的TAC数值有多少。通过上述算法,首先将欲存放此丛集的文件分别找出其在其他丛集时最小的相对成本,也就是第二个适合存放此文件的丛集。将每个文件相对成本比较并选出最小的,表示此文件被移出时增加的TAC最少,影响也最小。所以可决定将其移至别的服务器,如此重复挑选直到丛集空间足够。如由表4来计算结果如表5所示,可看出在丛集S2所有文件中,f3从丛集S2移至丛集所造成S3所造成的 TAC增长最少。所以在 S2满载时在移动文件档案会优先选择f3移出。

表5 文件移动增长成本Tab.5 Mobile cost of file growth
文件移出结束后回到主程序将会把相对矩阵重新计算一次,此时被移出的文件其存在第二个合适丛集的相对成本会变为 0,在下次重复挑选便会被第二合适的丛集选择。如此不断重复的选择、比较,直到所有文件都决定存放位置为止,完成文件最佳存放位置的近似解。
5 实验仿真
5.1 丛集数与分支度及文件数对存取成本影响仿真
在丛集数量与分支度对存取成本影响实验仿真中,分4种不同的丛集数及分支度进行交叉测试,丛集数分别为30/40/50/60,每个服务器丛集总空间为1000位元单位,丛集的连外分支数为1/2/3/4四种,入口点数固定为10,文件数固定为2000,每个文件的大小为3~5位元单位随机,使用者数为3000。图2为丛集数与分支度对存取成本影响的实验仿真结果。
丛集数与文件数对存取成本影响实验仿真中,以2种不同的丛集数与1000到4600文件数进行交叉测试,丛集数为30/60,每个服务器丛集总空间为1000,丛集的连外支数固定为 3,入口点数固定为10,文件数从1000到4600每次增加50个,每个文件的大小为3~6随机,使用者数为3000,图3为丛集数与文件数对存取成本影响的实验仿真结果。

图2 丛集数与分支度对存取成本影响Fig.2 The influence of cluster Number and branch degree on access cost

图3 丛集数量与文件数对存取成本影响Fig.3 The impact of the number of clusters and the number of files on the access cost
从图2可看出,四种分支度在不同服务器丛集数各进行10次的平均结果,在固定的文件与入口点数下,丛集数越多反而会增加存取成本。因为在没有相对提升分支度即提高每个丛集连外数情况下,增加丛集数同样会增加丛集间的跳跃计数从而增加了路径长度。提升分支度数后当丛集数增加时,因跳跃路径减少使存取成本增高率也相对下降,图 2中分支度到达 3时平均存取成本才约文件大小的3~4间,分支度到4时平均存取成本才在2~3间。
从图3中可看出,当文件数增加时,丛集数越多对存取成本的影响越低。当丛集数为30,当文件数增加时因丛集空间有限且丛集数较少,则必须将部分文件存放于距离较远的丛集,无法完全针对入口点需求量来存放文件,因此平均存取成本随文件数增加逐渐上升。而当丛集数为60时,平均存取成本在文件数增加时却逐渐下降,因为服务器较多则表示网络距离分布较远,入口点间的距离也会增加。而在文件少量时多数使用者会选择相同文件,所以文件便会被存放离多个入口点都不至于过远的中间丛集位置,则在网络结构分布较广状态下对每个入口点的距离都会多少增加,但当文件数增多会分散使用者选择的文件。部分用者选择的文件不一定为热门文件,不必存放于中间位置,可存放于针对存放该文件较多的入口点附近。而丛集数较多状态下,文件因空间不足被迫移至较远丛集的情况减少,相对的存取成本也会降低。因此文件数多时所有使用者的平均存取成本相对于文件数少时会较低。
5.2 随机和轮转存放方式对存取成本影响仿真
(1)丛集数对存取成本影响实验仿真
丛集数对存取成本影响实验仿真参数设定分为丛集数为30/60两种情况,丛集数为30/60的入口点数分别设定为5/15,服务器丛集总空间都设为1000位元单位,节点分支度都设为 3,频宽数值都设为2~8,文件数都设为1000~4600,文件大小都设为3~6位元单位,使用者数都设为3000。因丛集数多时丛集间的跳跃计数会增加,如入口点数与丛集少时设定相同,则入口点间的距离也会相对增加。所以在丛集数较多的实验仿真中设定有较多的入口以保证距离的公平性,仿真结果如图4所示。

图4 丛集数对存取成本影响Fig.4 The impact of cluster numbers on access costs
由图4可知,随机与轮转两种文件存放方法平均成本差距不大,且两种方法的存取成本与文件数没太多影响,而本文研究方法其平均存取成本相较于以上两种方法明显要低。且在文件总数相同条件下,丛集数为60时本文研究方法的平均存取成本与其他两种方法的差距大于丛集数为30时对应情况。即在储存空间充裕状态下本文研究方法能更有效安排文件的存放,而其他两种方法当丛集数增加后,因结构范围扩大提高了距离,从而使得平均存取成本大幅增高,由此可见本文研究方法在文件数与丛集数均衡情况下,更能将每个文件存放在有利于所有使用者的丛集位置。
(2)文件大小范围对存取成本影响实验仿真
仿真时文件大小随机范围分别设为4~6与1~9,丛集数都设为30,节点分支度都设为3,服务器丛集空间都设为1000位元单位,入口点数都设为5,频宽数值设为2~8,文件数设为1000~4600,使用者数设为3000,仿真结果如下图5所示。
由图5可知,本文研究方法与随机、轮转两方法当文件范围增加时,平均存取成本总体都有相对增加现象,且不管哪种文件大小范围,其平均存取成本数均大于文件大小范围。而本文研究方法当范围增加时,且文件数为1000~2350时因文件数较少易产生部分极端大小的文件,造成存取成本变异数较大;而当文件数超过2800后,存取成本变动范围明显缩小。表示即使文件大小的差异较大,本文研究方法仍然视使用者的使用情况处理极端大小的文件,不会造成因极度偏袒部分使用者而使整体平均存取成本降低。
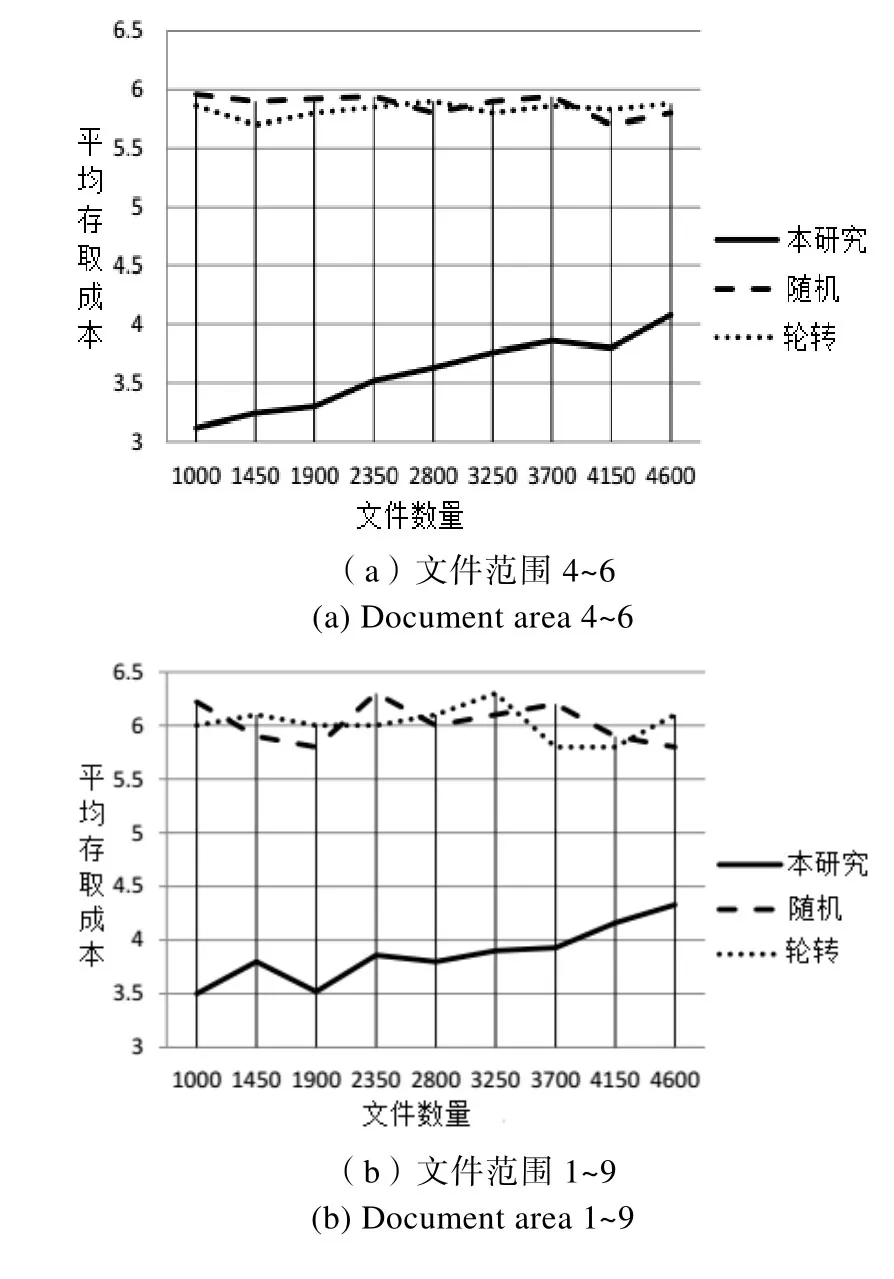
图5 文件范围对存取成本影响Fig.5 Scope of the file affects access costs
6 总结
本文所设计的云文件存放策略算法,针对客户端对文件的存取频率与文件大小,综合最短网络距离的计算来优选文件存放位置。通过弗洛伊得算法计算出任两点最短距离的特性,计算入口点至任意丛集的最短网络距离,让使用者能以最少的跳转次数或最佳的频宽路径进行存取,提升了效率。在分支度数实验中,当分支度增加使得路径选择变多时能计算出更佳路径,效率也相对提升。当多个使用者存取相同文件时,算法依据不同使用者存取入口点位置、存取文件大小、存取频率来计算出对所有使用者公平的存放位置,避免了文件只针对单一使用者情况来计算存放位置,造成其他多数使用者存取成本的增加。在丛集数与文件数实验中,本文研究的存放策略考虑到了所有使用者。当丛集存放空间满载时,本文研究的算法选出对使用者影响最低文件并移到别的丛集存放。当丛集数较少,且多数丛集空间都满载情况下,本研究方法仍然能够与其他两种方法有明显差距,证实本文研究算法能在丛集满载时,仍可计算出较佳的存放位置。
[1] 马小龙, 刘兰娟. 基于在线机制设计的私有云资源分配研究[J]. 计算机应用研究. 2015(2): 539-542.
[2] 徐晓斌, 张光卫, 孙其博, 杨放春. 一种误差可控传输均衡的WSN数据融合算法[J]. 电子学报. 2014(06): 1205-1209.
[3] 朱志祥, 许辉辉, 王雄. 基于云计算的弹性负载均衡方案[J]. 西安邮电大学学报. 2013(6): 43-47.
[4] 冯小靖, 潘郁. 云计算环境下的DPSO资源负载均衡算法[J]. 计算机工程与应用. 2013(6): 105-108.
[5] 裴养, 吴杰, 王鑫. 基于粒子群优化算法的虚拟机放置策略[J]. 计算机工程. 2012(16): 291-293.
[6] 刘媛媛, 高庆一, 陈阳. 虚拟计算环境下虚拟机资源负载均衡方法[J]. 计算机工程. 2010(16): 30-32.
[7] 刘春波, 陈建业. 基于SDN的虚拟网络重映射方法研究[J].软件. 2016(10): 82-88.
[8] 齐小航, 田清华. 空间信息网中面向任务的多拓扑路由算法[J]. 软件. 2014(9): 49-56.
[9] 赵礼峰, 梁娟. 最短路问题的Floyd改进算法[J]. 计算机技术与发展. 2014(8): 31-34.
[10] 陈雅良, 温朝晖, 周浩然, 王甜甜. 基于Floyd算法对交通流最优路径选择的研究[J]. 佳木斯大学学报(自然科学版).2016(6): 917-919+942.
[11] 许克平, 曾明月, 鄢好, 袁丽娟, 彭圆红. 基于不确定因素下的Floyd算法改进[J]. 中国科技信息. 2016(18): 49-50+14.
[12] 左秀峰, 沈万杰. 基于Floyd算法的多重最短路问题的改进算法[J]. 计算机科学. 2017(5): 232-234+267.
Research on Cloud File Storage Load Balancing Algorithm based on Floyd Algorithm
CHEN Yuan, LIU Jun-hua, LEI Chao-yang
(Internet engineering department, Hunan Post and Telecommunication College, Changsha 410015 China)
This paper proposes the cloud file storage load balancing algorithm based on Floydalgorithm, Based on the client′s access frequency and file size, the calculation of the shortest network distance to optimize the file storage location, and the hop count and network bandwidth between all clients and all service nodes are considered to be their network distance. The simulation results show that: In this paper, the average access cost of the paper is significantly lower than that of random and rotary methods, to place the file location fairly for all users, Allows users to access at least the number of hops or the best bandwidth path, improves the access efficiency of client file. And when most of the cluster space is full, the research methodcan still calculate the better storage location.
: Floydalgorithm; Cloud files; Load balancing; Algorithm
TP301
A
10.3969/j.issn.1003-6970.2017.10.012
本文著录格式:陈园,刘军华,雷超阳. 基于弗洛伊得算法的云端文件存储负载平衡算法研究[J]. 软件,2017,38(10):67-72
湖南省教育厅科研项目(编号:16C720)
陈园(1983-),女,湖南长沙人,讲师,硕士研究生,研究方向:图像处理、计算机网络;刘军华(1979-),男,湖南衡阳人,副教授,硕士,研究方向:移动互联网应用技术、软件工程;雷超阳(1971-),男,湖南耒阳人,教授,博士,研究方向:图像处理、计算机网络。

