一种基于最优匹配的低能耗栅栏修复方法*

戴光麟徐瑞吉王宇翔池凯凯毛科技

(浙江工业大学计算机科学与技术学院，浙江 杭州310032)

栅栏覆盖是无线传感器网络(Wireless Sensor Networks，WSN)覆盖研究的一个重要方向[1-2]，最早由Gage 在机器人研究领域提出，其通常用于监控特定区域入侵者的入侵与否和入侵轨迹[3]。 凭借传感器节点高效节能等优势，栅栏覆盖被广泛地应用于军事、工业、农业领域[4-5]。 栅栏构建后，特定区域集合内的相邻传感器节点检测区域相互叠加，保证至少有一个节点能够检测到入侵者并记录其入侵路径，可提高网络安全性[6-7]。 但在实际应用过程中，由于传感器节点所处环境复杂，栅栏易出现间隙导致丧失功能，因此需要及时并高效完成栅栏修复[8-9]。

目前国内外对栅栏间隙修复的研究已取得很多成果。 文献[4]提出了一种用于移动传感器节点的k - 栅栏覆盖算法(An autonomous deployment algorithm for k-barrier coverage with mobile sensors，MobiBar)，通过构建k 个不同的完整栅栏，利用有限的传感器节点提供了最大程度的栅栏覆盖，并利用可移动节点，使栅栏能够自我修复和重建；文献[10]提出了一种k 栅栏覆盖方法，通过几何数学模型优化节点位置，仅通过启动睡眠的节点，即可完成栅栏间隙的修复，与采用可移动节点修复栅栏的方式相比，解决了可移动传感器节点高能耗的问题，降低了栅栏间隙修复的总能耗。 在寻找最优修复路径的算法上，文献[11]引入了概率感知模型寻找最佳修复路径，使用最大权匹配算法(Kuhn-Munkres，KM)调动移动节点完成栅栏修复；文献[12]提出了一种基于概率感知模型的FDS-AD 算法，通过人为设定的概率阈值调动可移动传感器节点，确定最佳修复路径的同时，兼顾了能耗；文献[13]则提出了一种WSN 栅栏间隙修复优化方法(An Optimization Method for WSN Barrier Gap Repair，OMBR)，利用k条最短路径算法(Top-k-Shortest Paths，KSP)寻找所需可移动节点数量最少的可修复路径，减少移动节点的能耗。 在降低可移动传感器节点派遣能耗的算法中，文献[14]提出了一种Optimal 栅栏间隙修复方法，定位到栅栏间隙位置后，通过二分法派遣可移动节点完成间隙修复，可有效缩短可移动节点的移动距离；文献[15]通过梯度差分算法确定关键节点，在使用二分法派遣节点时引入决策算法进行优化，确定节点移动的最短路径。

实际应用场景中，在构建栅栏初期，使用的节点仅占少数，大部分节点作为备用，当栅栏被破坏时才会接替运行并修复栅栏。 考虑到一般情况下可移动节点的成本往往非常高，在修复栅栏间隙时，需要充分考虑如何匹配最优的可移动节点，实现低功耗栅栏修复[16]。 将上述文献与实际情况结合分析，本文提出了一种基于最优匹配的低能耗栅栏修复方法(Low-Power Barrier Coverage Repair Method Based on Optimal Match，BCR-OM)，该方法首先遍历栅栏搜索栅栏间隙；然后计算完整修复栅栏间隙，所需的可移动传感器节点的最小数量；随后利用传感器节点构建栅栏间隙修复路径；最后利用Hungarian 算法得出节点的最佳派遣方案，将节点派遣至对应位置，使用较低能耗完成栅栏间隙的修复。

1 栅栏间隙搜索

1.1 相关假设与定义

假设在栅栏间隙搜索开始前，栅栏构建已完成。在特定的带状区域内，部署的可移动节点传感器节点和静态传感器节点按照特定比例存在，且所有传感器节点的位置已知(通过汇聚节点定位自身位置)，当传感器节点感知到栅栏中出现间隙后，派遣可移动传感器节点至待修复的位置，即可完成间隙修复。

如图1 所示，图中为一条带状栅栏，节点ni和节点ni＋1之间出现栅栏间隙，此时，间隙周边存在可移动传感器节点m，如果将节点m派遣至栅栏间隙处，即可修复栅栏。 假设传感器节点m的最大可移动距离为D，可感知的范围是半径为R的圆形区域。

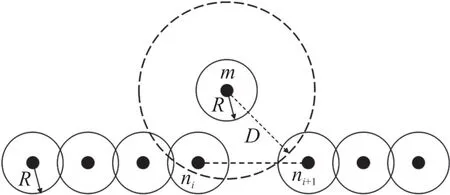
图1 栅栏间隙图

1.2 栅栏间隙搜索算法

在进行栅栏间隙修复前首先需要查找出栅栏间隙的位置。 由于栅栏中所有传感器节点的坐标都已经获得，且传感器节点的感知半径都为R，因此基于传感器节点之间的距离和感知半径判断栅栏中两个相邻传感器节点之间是否存在间隙，当两相邻节点的距离大于2 倍感知半径，则可认为栅栏存在间隙。表1 详细介绍了本文提出的栅栏间隙搜索方法，该算法将搜索到的栅栏间隙保存在集合Gap 中，该集合是一个n行，2 列的数组，Gap(i，1)记录该间隙的前一个传感器节点编号ni，Gap(i，2)用于记录栅栏的间隙长度L。

图2 栅栏搜索过程图

对于节点nt，执行步骤3 ～7 具有常数复杂度。因为需要对栅栏中num 个节点依次执行步骤3 ～7，因此算法的总复杂度正比于栅栏节点数目num。 如图2 所示，传感器节点nt与nt＋1之间存在栅栏间隙，且为搜索到的第一个栅栏间隙，则Gap(0，1)＝t，Gap(0，2)＝d-2R。

表1 栅栏间隙搜索算法

2 栅栏间隙修复

2.1 确定可修复间隙数量

在进行栅栏修复前，首先要基于冗余的静态节点及其位置，在充分利用静态节点的前提下，确定所存在的间隙的位置、间隙的数量、间隙周围的可移动节点数量是否满足间隙修复要求。

寻找到待修复的栅栏间隙后，即可开始对栅栏间隙进行修复。 将待修复的栅栏间隙平均分段，分段数量记为mnum，如式(1)所示。

因传感器节点覆盖最大长度为2R，对式(1)上取整。 分段后，如图3 所示，子间隙的中心点gi、gi＋1、gi＋2就是该段栅栏间隙的待修复位置，将可移动传感器节点派遣至gi、gi＋1、gi＋2即可完成栅栏间隙修复，此时mnum即为最少派遣的可移动传感器节点数。

图3 栅栏间隙修复过程图

修复栅栏间隙应首先考虑最大修复率，其次考虑最小化修复代价。 如图4 所示，节点S和D之间出现栅栏间隙，以节点S为起点，节点D为终点，结合间隙周围的冗余静态节点构建全连接拓扑图G＝(V，E)，V是静态节点集合，如式(2)所示，其中nw表示静态节点，w表示G中静态节点数量，E是节点间构成的边的集合，如式(3)所示，ei，j表示节点ni和nj之间的边，sn＝w＋2。

图4 静态节点全连接拓扑图

以numi，j表示节点ni和nj之间的边被节点感知范围完全覆盖所需最少传感器节点的数量，其值如式(4)所示，d(ei，j)表示节点ni和nj之间的距离，r表示节点的感知范围，1 ≤i，j≤sn。

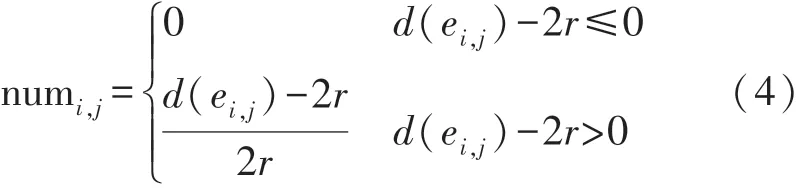
一旦计算完每对静态节点间(包括S、D节点与静态节点间)修复所需的最少移动节点数，即可确定需要可移动节点最少的一条由S到D且中间经过部分静态节点的路径Path，随后即可在该路径上确定待修复位置以及所需要的可移动节点数量。 此时Path 中所包含的静态节点已经被选定参与到S和D之间的间隙修复。

2.2 基于Hungarian 算法的栅栏修复

选择静态节点参与栅栏间隙修复后，节点仍可能存在间隙，此时需要利用周围可移动节点完成修复。 为保证间隙修复的代价最小(即可移动节点在修复过程中的移动距离和最小)， 本文利用Hungarian 算法来选择可移动传感器节点，从而使修复后可移动节点在修复栅栏间隙移动过程中消耗总能量降低。 Hungarian 算法是一种最优化指派算法，如指派g个人去做g个任务，每个人对不同任务的熟悉程度不同，利用Hungarian 算法可选择最合适的人去做某一项工作，使得g个人完成g个任务所花的时间之和最短[13]。 不同的人完成不同的任务所需的时间，可以用n维方阵来刻画，称为代价矩阵，如式(5)所示。

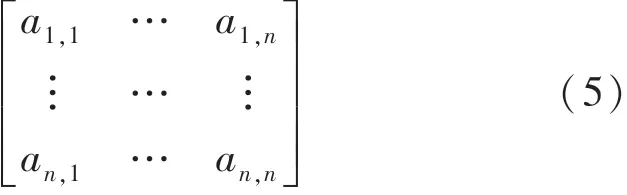
式中:ai，j表示工人i完成第j项任务时所需的开销。

Hungarian 算法对矩阵进行一系列操作，当矩阵中出现n个满足不同行不同列的0 时，算法停止，此时即可确定哪个工人去执行哪项任务。 具体步骤如下:①每行减去此行最小数②判断是否达到算法目标，如未达到算法目标，继续下一步。 否则结束。③行列交替寻找没有选中0 的行或列。 首先按行找到没有选中0 的行(具体见步骤实例)，在找到的行后标记；随后标记该行中有0 的列。 在已标记的列中，如果有0，继续标记有0 的行，交替标记后，直到所有目标行列都被标记。 ④将未标记的行与已标记的列划线，即可划去矩阵中出现的所有0，随后在剩余元素中寻找最小的值min。 ⑤将步骤④中划线的行减去min(若元素为0，变成-min)，然后将划线的列加上min(另矩阵元素全部大于等于0)。 返回步骤②。

利用Hungarian 算法分析节点派遣问题。 当修复位置总数z大于可移动节点总数t时，无法完成间隙的修复，此情况不在本文的考虑范围内。 当修复位置总数z小于等于可移动节点总数t时，通过派遣t个可移动传感器节点至z个待修复位置实现栅栏间隙修复，此时每个待修复位置接受一个可移动传感器节点，剩余t-z个节点无需移动。 在修复路径上虚拟出t-z个虚拟修复位置，使t个可移动节点被派遣到t个修复位置，具体方法如图5 所示，共分为两种情况:修复位置总数等于可移动节点总数；修复位置总数小于可移动节点总数。

图5 间隙修复过程情况图

图5(a)间隙修复路径中存在2 个待修复位置，可移动的传感器节点数分别为mn1和mn2，节点mn1可以移动到位置a，移动距离为d1，但无法移动到位置b(因为其余位置b的距离大于最大可移动距离D)，因此定义可移动传感器节点mn1与待修复位置b的距离为＋∞；节点mn2与位置a和位置b的距离均小于D，因此能够移动到位置a与位置b，且移动距离为d2与d3，利用可移动传感器节点与待修复位置的距离作为修复栅栏间隙的代价，构建Hungarian 算法的代价矩阵，如式(6)所示。

图5(b)间隙修复路径中存在2 个待修复位置，而可移动节点有3 个，分别为mn1、mn2和mn3，此时需要虚拟一个待修复位置，如图中虚拟位置O所示。 假设所有可移动传感器节点与虚拟待修复位置O的距离都为0，当可移动传感器节点与待修复位置的距离大于节点的最大移动距离D时，则定义该节点与待修复位置的距离为＋∞。 构建的Hungarian算法代价矩阵如式(7)所示。

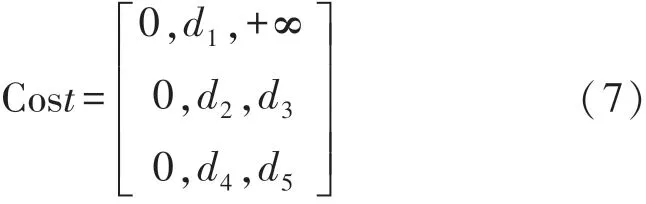
3 仿真实验及分析

本实验采用MATLAB 进行仿真测试，MATLAB软件运行在i5-9400F 处理器、16G 内存的PC 机上。实验开始前，将静态传感器节点和可移动传感器节点按照特定比例混合，随机均匀地放置在一个长为1 000 m，宽为200 m 的带状区域中，实验中的传感器节点感知范围为半径R＝50 m 的圆形，构建的栅栏如图6 所示。 实验分析了本文提出的BCR-OM方法的相关性能，在栅栏修复方面与文献[14]提出的Optimal 方法、贪婪算法(Greedy)进行对比。 在栅栏构建阶段，主要能量消耗发生在可移动节点移动过程中，而在感知方面的能量消耗较少，因此传感器节点感知的能耗忽略不计(节点移动能耗远高于感知能耗)。 移动1 m 消耗能量为3.6 J。

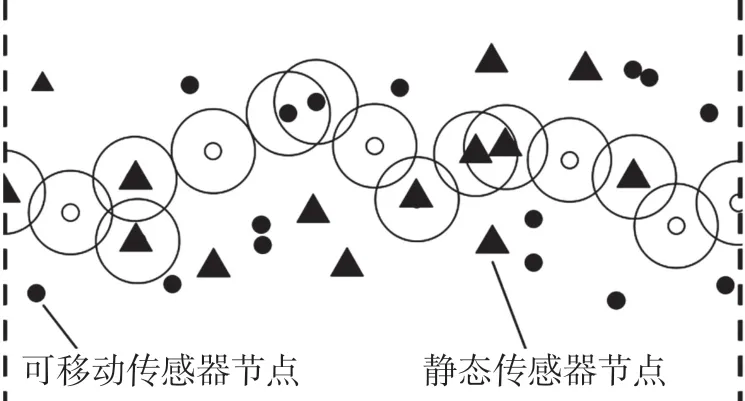
图6 间隙修复结果图

3.1 栅栏间隙修复实验

文献[14]提出的Optimal 栅栏间隙修复方法首先定位到间隙所在位置，然后计算需要的可移动节点数量，最后派遣可移动的传感器节点移动至对应的待修复区域完成栅栏间隙修复。 在派遣过程中，它使用二分法优化减少节点的移动距离，同时使用Greedy 算法派遣最近的可移动传感器节点修复栅栏间隙。 而本文提出的BCR-OM 栅栏间隙修复方法首先寻找可以使用的静态传感器节点，当静态传感器节点不能完成栅栏修复时，派遣可移动节点修复栅栏。 在带状区域中部署100 个传感器节点，可移动节点占30%，静态节点占70%，可移动节点最大移动距离R ＝200 m。 由于传感器节点的感知能耗较小，相对于可移动传感器移动位置产生的能耗可忽略不计，栅栏修复能耗主要来自于可移动传感器节点的移动产生的能耗，因此本实验调整间隙的长度来模拟不同环境，通过对比修复间隙所需能耗来对比算法效率。 实验结果如图7 所示。

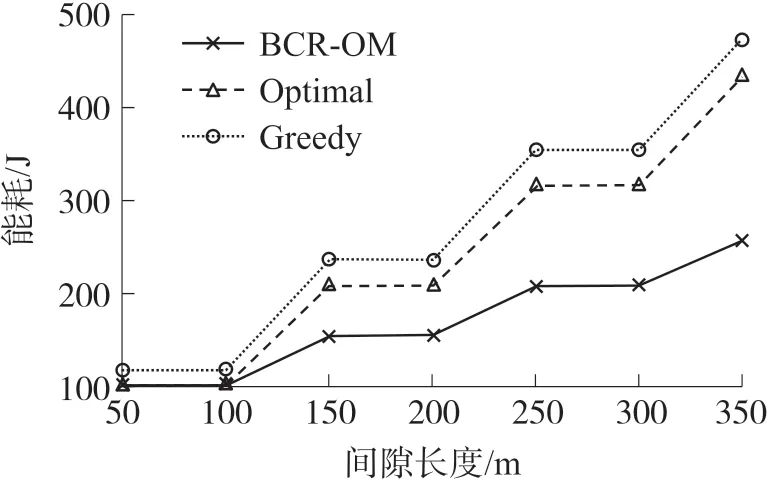
图7 栅栏修复能耗图

在栅栏间隙修复方面，随着栅栏间隙长度的增加，三种栅栏修复方法修复栅栏的能耗呈梯度升高，因为栅栏间隙为50 m 和100 m 时需要的可移动节点数量相同，250 m 和300 m 需要的移动节点数量相同，因此消耗的能耗呈梯度提高。 且BCR-OM 方法的能耗低于Optimal 方法和Greedy 方法，因为BCR-OM 首先考虑使用静态节点修复栅栏间隙，当静态节点不能完成修复时，再派遣可移动节点，因此需要调度的可移动节点数量相对其他两种方法较少，节点移动的总距离更短，消耗的能量更低。

考虑到实际场景中栅栏并不能够完全被修复，在栅栏间隙长度不同的情况下，若仅考虑修复能耗，无法确定算法修复效率，必须与栅栏修复成功率结合，才能对比相关算法的效率，因此需要引入栅栏修复率这一参数用于描述修复情况。 在栅栏修复率方面的实验如图8 所示，实验结果表明随着栅栏间隙长度的增加，栅栏修复成功率会逐渐降低，栅栏间隙长度增加，则需要的可移动节点数量增加，而可移动节点存在最大可移动距离R，因此修复率逐渐降低。BCR-OM 方法的栅栏修复成功率最高，在栅栏间隙长度为350 m 时，比Optimal 方法提高了8%左右，比Greedy 方法提高了12.6%左右，Optimal 方法的修复成功率高于Greedy 方法。

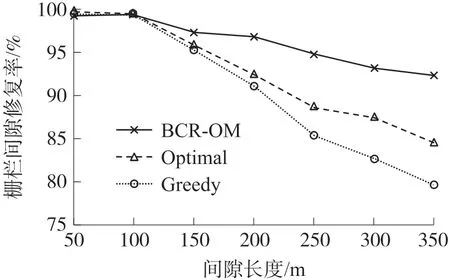
图8 栅栏修复率图

3.2 节点平均移动距离对比实验

本文方法(BCR-OM)修复栅栏间隙理论上能够保证栅栏中所有间隙的修复代价最小。 通过栅栏间隙修复实验，可发现当部署的可移动传感器节点较少时，由于间隙过长，可移动传感器节点无法确保间隙修复率达到100%，因此本实验将可移动传感器节点数作为参数，通过对比可以的节点数量确定的情况下，完成修复时节点的平均移动距离，实现算法效率的对比以及可靠性比较。 此处将本文提出的方法与Greedy 算法进行对比，研究修复栅栏间隙过程中，可移动传感器节点的移动的平均距离。 实验中，将可移动传感器节点的最大可移动距离D设置为30 m 和40 m。 实验结果如图9 所示，横坐标为栅栏构建初期部署的可移动传感器节点的数量，纵坐标表示完成栅栏间隙修复后，可移动传感器节点的平均移动距离(m)。

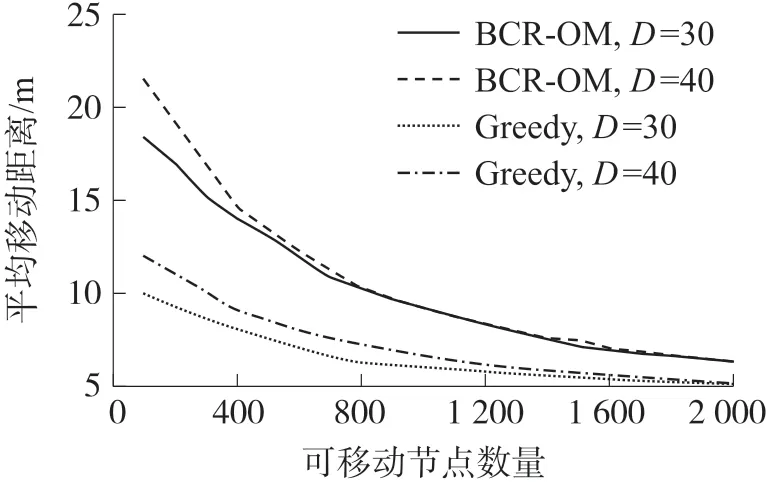
图9 节点平均移动距离图

从图9 的实验结果图中可以看出，当可移动节点的最大可移动距离相同的情况下，本文提出的BCR-OM 方法修复栅栏时可移动节点的平均移动距离大于Greedy 算法。 这是因为Greedy 算法总是派遣局部最接近待修复位置的可移动节点修复栅栏间隙，然而这种修复方法，经常会出现无法修复的情况，其实这些用Greedy 算法无法修复的情况，很可能用BCR-OM 方法是能修复的。 结果图中Greedy算法的节点平均移动距离，为修复成功情况的平均结果，不含未修复成功的实验情况。 本文的BCROM 方法对所有待修复位置进行宏观考虑，对于能修复的情况，确保了找出代价最小的修复方案来，在确保能修复的场景都被修复该条件下，实现总体修复代价的最小化。 由于BCR-OM 方法所对应的平均移动距离，是对所有能修复的情况进行统计平均的，所以才出现了平均移动距离略大于Greedy 算法的平均移动距离的情况。 就单个Greedy 算法也可修复的场景来说，BCR-OM 方法的节点总移动距离一定小于Greedy 算法所对应的节点总移动距离。

从图9 中还可以看出随着可移动节点的最大移动距离D的逐渐的增加，其平均移动距离也在增加。

4 总结

本文主要介绍了一种基于最优匹配的低能耗栅栏修复方法，该方法主要研究如何派遣可移动节点修复栅栏间隙使得修复代价最小。 仿真实验结果表明本文提出的栅栏间隙修复方法在修复率以及修复代价上都优于传统的栅栏修复方法。 但是在成功修复的情况下，本方法的修复代价还是略高于Greedy算法。 考虑到实际应用环境往往较为复杂，仿真实验太过理想化，本研究接下的工作拟搭建一套真实硬件网络构成的测试平台，通过半仿真实验，进一步完善本文栅栏修复方法。