LS-SVM的核参数对概率筛筛分效率预测影响

杜锦程 ，吴福森，陈丙三

(1.福建工程学院 机械与汽车工程学院，福建 福州 350118；2.福建省特种设备检验研究院 泉州分院，福建 泉州 362011)

概率筛是筛分作业中使用最广的设备之一[1-2]。在实际应用中，概率筛的结构及运行参数的选择主要依据振动机械设计理论中参数的设定范围，结合不同行业的实际使用状态加以改进。为了提高概率筛的筛分效率，获得概率筛的最优运行参数或结构参数，国内外学者开展了许多相关研究。Davoodi等[3]研究了孔径在不同材料中的变化，以及孔径形状和筛选介质材料的不同对筛选性能的影响，利用离散元法(DEM)建模模拟筛分过程明显提高了筛分的分辨率。Ferenc等[4]通过对单球颗粒在振动筛非惯性参照系中的运动分析，确定了振动筛的最佳振动参数。郑桂霞等[5]应用支持向量机算法，建立预测模型来预测不同的概率筛结构参量和运行参量条件下的筛分效率，得出支持向量机在小样本、非线性及高维模式下识别问题中表现的许多优势[6-7]。黄宜坚[8]利用基于自回归 (AR) 模型估计的双谱及其对角切片, 找出谱特征与筛分效率之间的相关性。

上述研究针对筛分效率的建模分析与预测精度均与核函数的选择及参数设置有关，但目前针对筛分效率的预测精度仍然有局限性。核函数的选择对概率筛预测精度有较大影响，本研究将最小二乘支持向量机分类算法(least squares support vector machine，LS-SVM)引入自同步概率筛筛分效率预测建模，同时探讨核函数对LS-SVM 预测精度的影响通过网格搜索法和交叉验证法来选择合适的核函数进行预测精度研究，并应用于概率筛振动参数与筛分效率之间的关系研究，为概率筛结构的进一步改进提供依据。

1 LS-SVM的建模

Vapnik等人早在20世纪70年代就已经建立了统计学习理论的基本体系，系统研究了机器学习的问题，尤其是有限样本情况下的统计学习问题[9]。LS-SVM方法是Suykens[10]于1999年在支持向量机基础上提出的改进算法，主要针对大规模数据集的处理、处理数据的鲁棒性、参数调节和选择问题、训练以及仿真。

模型描述：将不等式约束条件转变成等式约束，使求解过程变为线性的运算，保证分类精度的同时简化了计算量，其训练通过式(1)完成[10-11]：

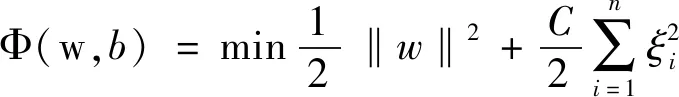
(1)

s.t.yi=wT·g(xi)+b+ξii=1,2,…,n

式中，x为输入数据；y为输出数据；w为权重向量；g(xi)是将x从输入空间映射到特征空间的函数；ξ是xi的松弛系数，C是边界系数。式(1)的Lagrange目标函数为：

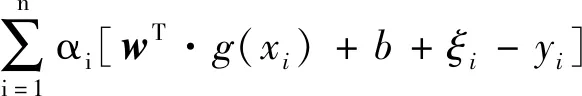
(2)

令式(2)对w,b,ξ的偏导为零，可得：

(3)

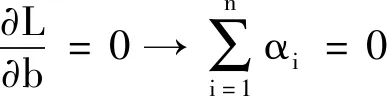
(4)

(5)

将式(1)～(4)结合式(5)的条件消去w,ξ可以得到一个线性系统：

(6)

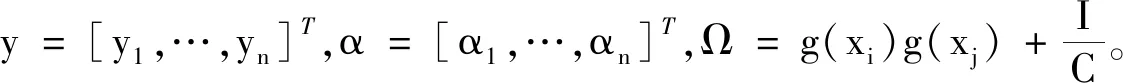
为了避免直接处理变量的空间映射，可以利用核函数K(xi,xj)=g(xi)g(xj)来减少计算维度以此来降低计算的复杂度。

求解矩阵式(6)可解得α和b，代入(3)求解出w后得到回归函数：

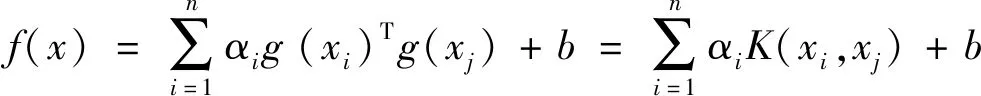
(7)

2 概率筛筛分实验

2.1 筛分效率的计算

概率筛以概率筛分理论为基础，产品物料粒度筛分级别与筛网网孔直径不完全吻合，筛分出的各种粒度级别产品会混有其他粒度级别的颗粒。为了适应概率筛筛分效率计算公式，美国学者R·T·汉考克于1918年提出总效率公式(汉考克效率)来解决这一问题，其式如下：

筛分总效率(η)=

目的物的回收率(η1)- 非目的物的混杂率(η2)

(8)

目的物的回收率：

(9)

非目的物的混杂率：

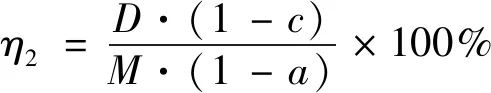
(10)

筛分机入料口的物料总量M和筛上的物料总量U及筛下物料总量D满足关系式：

M=U+D

(11)

M·a=U·b+D·c

(12)

由式(11) 和(12)可以推得：

(13)

再将式(13)代入式(8)中得：

(14)

式中，a为原始物料中小于规定粒度的物料质量所占总质量的比值；b为筛上物料中小于规定粒度的细粒物料占总质量的比值；c为筛下物料中小于规定粒度的细粒物料占总质量的比值，其中规定粒度是根据用户对产品的粒度要求而确定的。筛分总效率公式是反映筛分过程的综合指标。

2.2 筛分实验

实验主要研究设备包括料仓、给料器、螺旋输送器、 Gls10概率筛以及GLs10概率筛样机，对干沙的处理量达到每小时5.0 t，使用的筛网尺寸为800 mm×600 mm，筛网规格为0.7 mm×0.7 mm。

根据自同步概率筛工作原理，确定实验过程中对概率筛筛分效率有较大影响的4个工艺参数，并针对这4个工艺参数进行不同参数的自同步概率筛筛分实验。为了对筛分效率进行对比验证，给料速度设为2.0 t/h和3.0 t/h，由经验可知振动圆频率一般为700～1200 r/min，实验分别对振动圆频率为700、750、800、850、950、1 100、1 200 r/min的情况进行实验。筛网倾角选择18°、19°、20°、21°、22°、26°，振幅选择范围为3～7 mm，此时筛分效率变化明显。本次试验筛分产品规定粒度为0.6 mm，实验结果如表1所示。

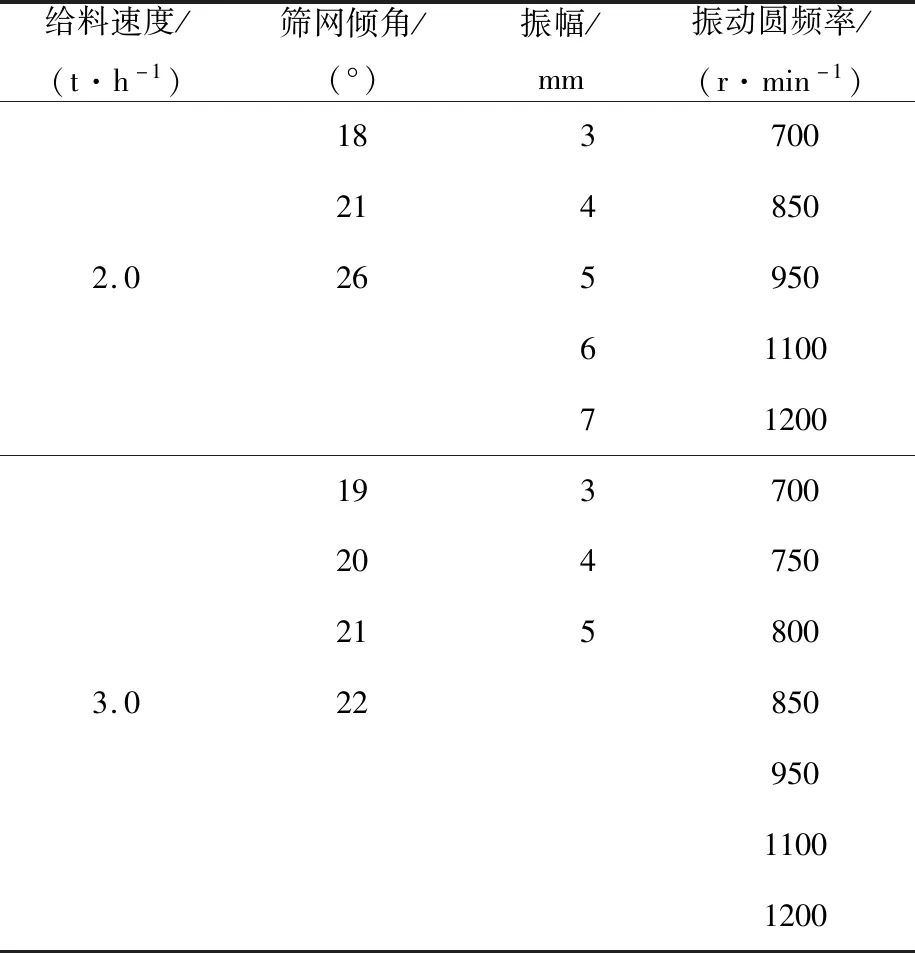
表1 自同步概率筛实验安排Tab.1 Experiment arrangement of the self-synchronous probabilistic sieve

实验结合不同的振动参数进行多次筛分实验，记录不同出料口的物料质量，确立不同出料口物料的颗粒大小的含量情况，研究不同振动参数的筛分性能。以自同步概率筛实际筛分数据作为LS-SVM模型预测的实验及学习对照样本，部分参数配比在实际中无法测出，将其当作预测样本。

2.3 实验数据预处理

对自同步概率筛不同振动参数情况进行筛分实验，计算不同筛分作业情况的筛分效率。由于实验过程中人为因素的影响，导致部分粗大误差数据点，因此需要对筛分记录数据进行预处理，通过分析筛分效率的变化趋势，根据实际情况对于筛分效率与整体变化趋势相悖较大的实验数据，认为该次实验数据有误，应当剔除，以此提供准确的数据进行筛分概率的研究分析。图1和图2分别表示给料速度为2.0、3.0 t/h，振幅固定时的概率筛筛分效率出现粗大误差数据随振动频率的数据变化情况，图中三角形标记的数据点是误差点，剔除这部分数据后建立自同步概率筛筛分效率预测建模的支持向量机样本库。

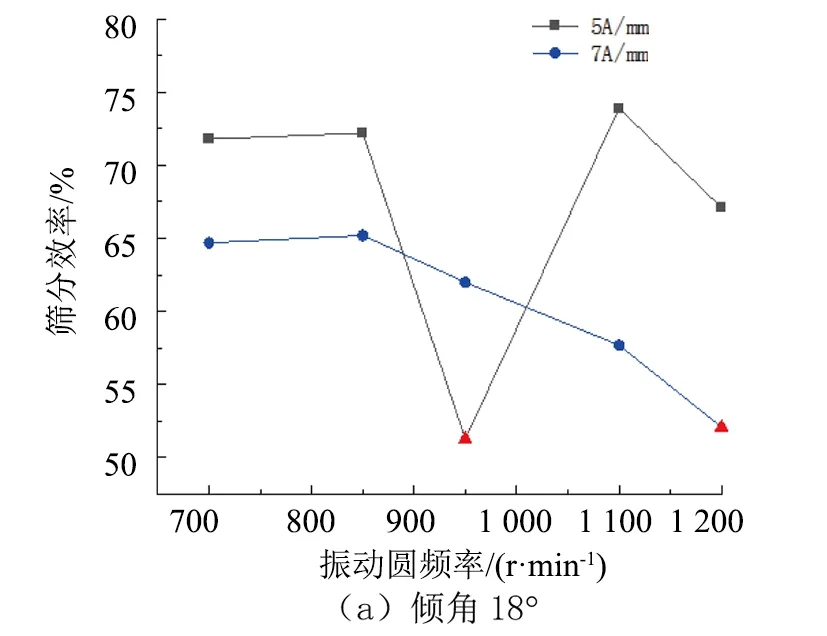
图1 不同振动参数的筛分效率分布情况(给料速度2.0 t/h)Fig.1 Distribution of screening efficiency of different vibration parameters (feeding speed 2.0t/h)

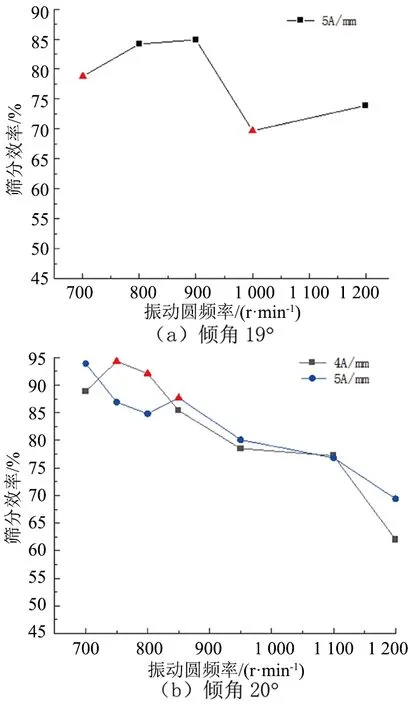
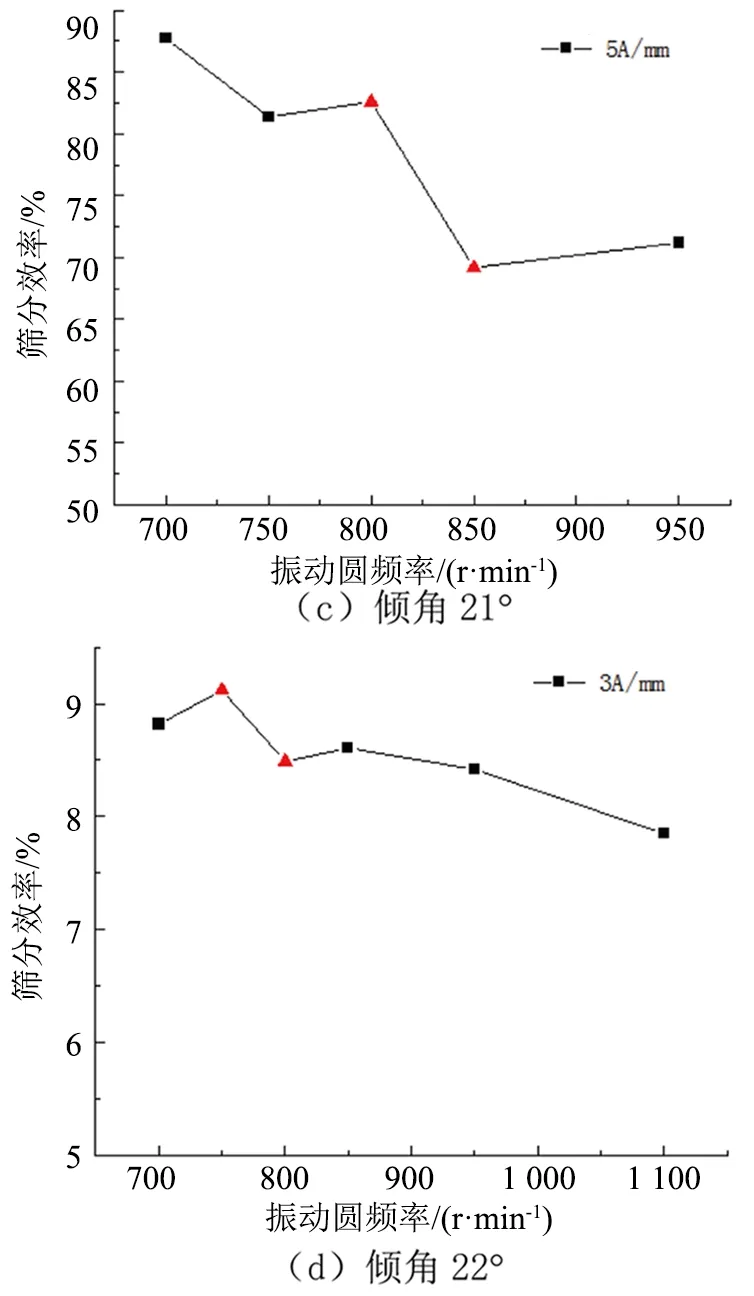
图2 不同振动参数的筛分效率分布情况(给料速度3.0t/h)Fig.2 Distribution of screening efficiency of different vibration parameters (feeding speed 3.0t/h)

3 LS-SVM筛分效率预测实验步骤

模式识别是一种对输入数据进行诊断并根据诊断出的类别采取相应行为的学习方法。其基本实现过程是预处理、特征提取和分类。利用LS-SVM算法建立一个概率筛筛分效率的分类器对输入数据赋予一个类别标记，研究该分类器的可靠性以及推广能力，该LS-SVM筛分效率预测模型是利用MATLAB 2018编写最小二次支持向量机程序来实现的，实验数据为自同步概率筛筛分实验记录的不同参数下的筛分效率情况。程序流程如图3所示。

图3 LS-SVM模型建立流程Fig3 LS-SVM model building process

(1)数据预处理。实验中对各种参数情况下自同步概率筛筛分产品进行收集，记录各筛面出口产品重量，利用上述总效率公式计算各种工况下概率筛筛分效率。

(2)确立LS-SVM模型数据样本。将影响概率筛筛分性能的因素，即给料速度、振动圆频率、筛面倾角和筛面振幅4个参数指标，记为xi；分类阈值标准yi，我们规定筛分效率大于80%的样本记为y=1，筛分效率小于80%的样本记为y=-1。

(3)输入学习样本(xi，yi)。将实验获得的130组数据分成两部分，其中100组作为训练样本，30组作为预测样本。

(4)对学习样本进行参数寻优，通过网格和交叉算法，对核参数的选择进行优化，并以此进行LS-SVM模型的训练。

(5)把预测样本输入已建立的LS-SVM模型进行计算，将计算结果与实验真实值比较，误差采用错分率e来评价LS-SVM模型的推广能力，如式(15):

(15)

4 核函数对预测建模的影响研究

合适的核函数参数和误差惩罚因子，能够增强LS-SVM模型的推广性能。为了研究将LS-SVM算法引入概率筛筛分效率预测建模的可行性，同时选用不同核函数进行LS-SVM的建模，比较3种常用核函数的建模预测情况。

4.1 多项式核函数建模结果

采用多项式建模情况下，误差惩罚因子C的改变对模型预测精度影响较小，而多项式核函数阶数d的改变对模型预测精度影响较大。采用多项式核函数建模，预测结果如表2所示。比较各个参数情况的建模结果，只在多项式阶数d=2时建模预测精度最好，最高识别率达到96.7%，达到建模预测效果，所建模型有较好的泛化能力，但是学习能力不足，并且多项式核函数的阶数比较高时核矩阵的元素值将趋于无穷大或者无穷小，计算复杂度会大到无法计算。

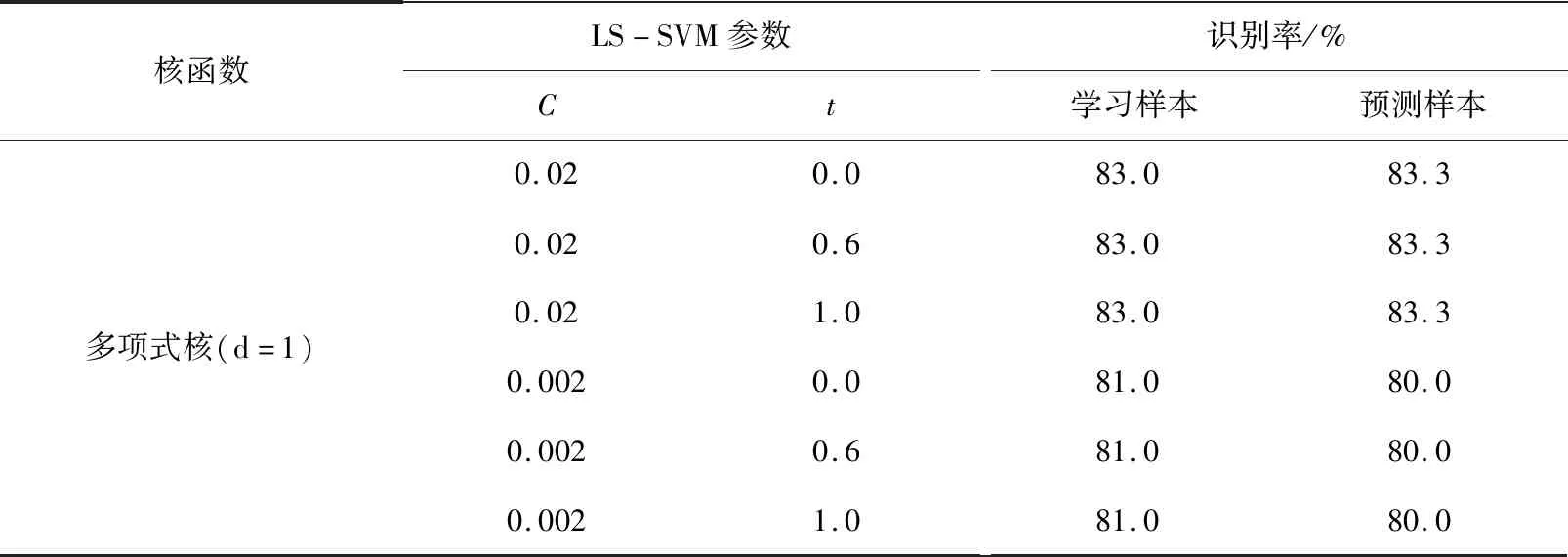
表2 多项式核函数建模分类情况Tab.2 LS-SVM classification by using polynomial kernel function

续表2

4.2 RBF核函数建模预测结果

观察表3可得，误差惩罚因子C在一定范围内增大能够提高模型的识别率，而RBF核参数σ2的增大致使模型的识别率下降，所以建模时综合考虑二者影响情况，合理选择C和σ2使模型的识别率达到最高。采用RBF核函数建模预测获得理想结果，当参数C=2和σ2=15；C=20，σ2=60；C=50，σ2=60时模型预测识别率都达到100%，达到理想建模预测效果，表明采用RBF核函数建模预测是可行的，所建模型具有较高的泛化性能。

表3 RBF核函数建模分类情况Tab.3 LS-SVM classification by using RBF kernel function

4.3 Sigmoid核函数建模预测结果

由表4可得，采用Sigmoid核函数建模预测不够理想，无论对学习样本还是对预测样本的识别率都低于80%，建模分类效果最差，因此Sigmoid核函数不适合应用于自同步概率筛筛分效率预测建模。

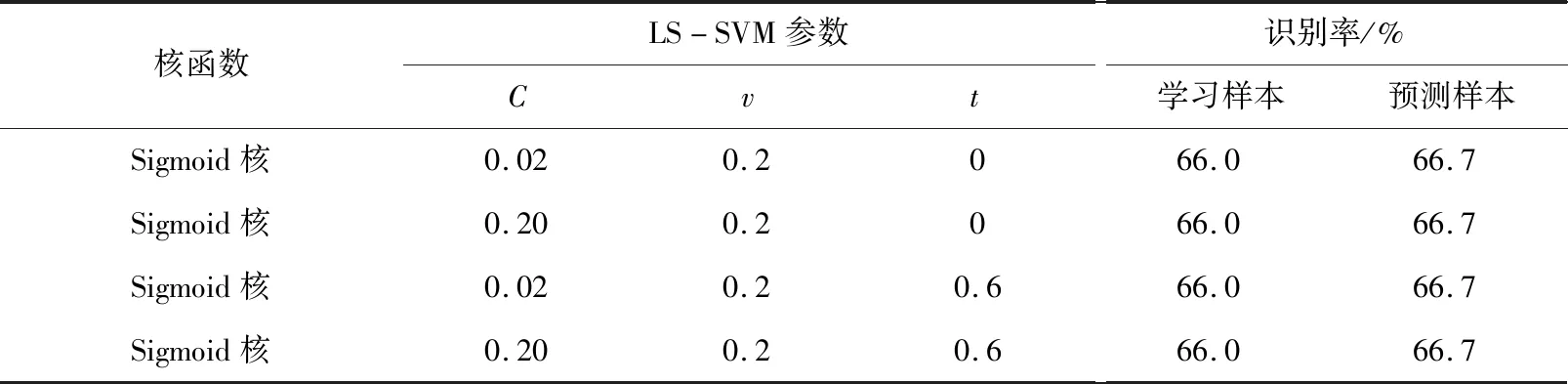
表4 Sigmoid核函数建模分类情况Tab.4 LS-SVM classification by using Sigmoid kernel function

选择采用将交叉验证法(CV)和网格搜索法结合的方法运用MATLAB程序自动对核参数进行寻优，获得优化核参数为C=9.5和σ2=56.6，计算预测样本的估计输出与实验值的相对均方误差为e=1.44%，预测结果如图4所示。

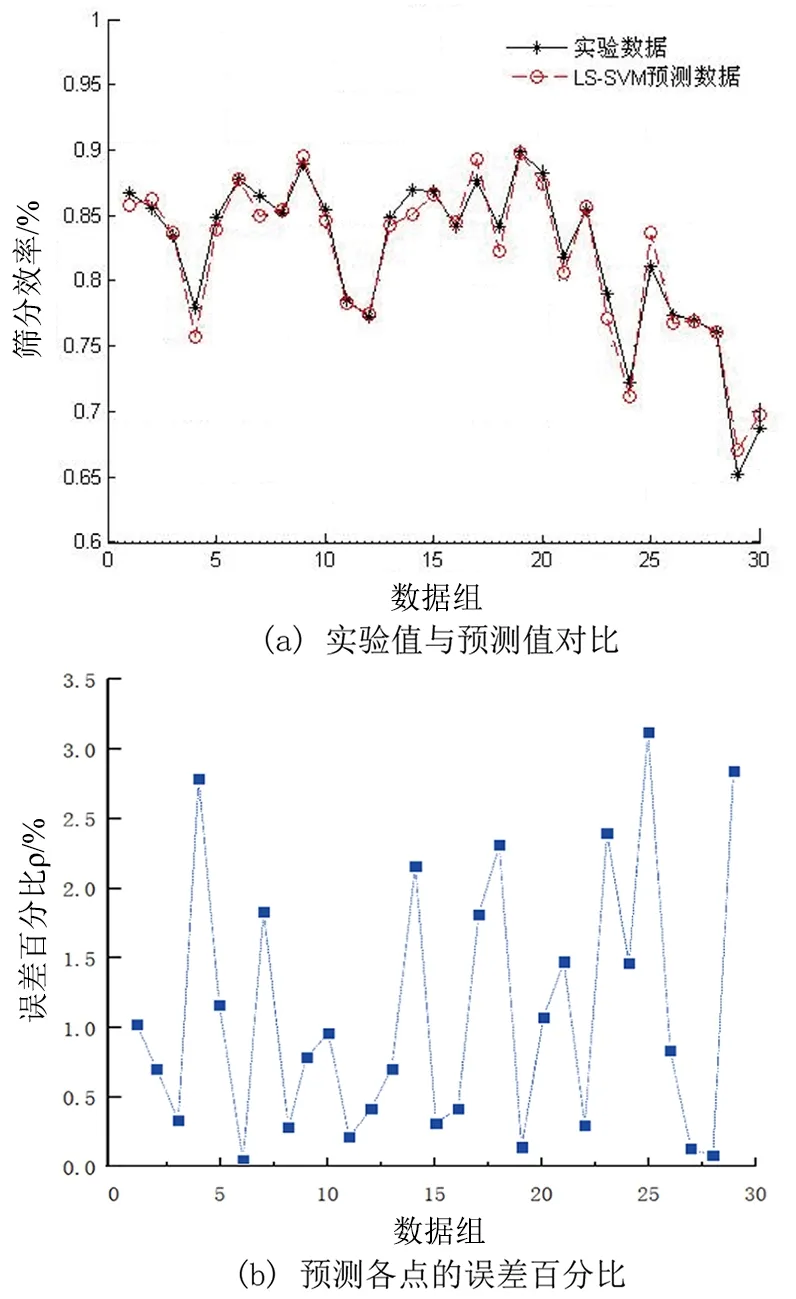
图4 LS-SVM建模的实验值与预测数据比较Fig.4 Comparison of LS-SVM modeling experimental values and predicted data

观察图4中LS-SVM模型预测出的筛分效率值与对应的实验中各中工艺参数下概率筛所获得的筛分效率值大小非常接近，单次最大误差百分比为3.14%。LS-SVM比S-SVM大大简化了运算算法，但由此却给建立的LS-SVM模型带来了鲁棒性的不足，因此采用加权的方法来提高LS-SVM模型的鲁棒性。对已经建立的LS-SVM模型，再进行Weighted LS-SVM建模，增强模型的鲁棒性，进行了鲁棒性训练后的预测结果，相对均方误差e=1.22%，模型预测精度有一定的提高，单次预测最大误差百分比下降为2.27%，表明此模型具有更强的推广能力，进一步表明基于LS-SVM的概率筛筛分效率预测建模的优越性。

5 结论

分析3种核函数实验建模预测结果，可以得到这样的结论：1)采用多项式(Poly)核函数和RBF核函数建模预测都取得理想效果，Sigmoid核函数建模预测不够理想，分类效果最差。2)Poly核函数是一个全局性函数，具有较强的泛化能力，但是学习能力较弱是导致实验模型预测识别率不高的主要原因。3)RBF核函数是一个典型的局部性核函数，泛化能力不如Poly核函数，仅仅在测试点附近小领域类对数据点有影响，因此当预测样本数据在学习样本数据点附近时，建模核函数选用RBF核函数为最佳。4)实验建模预测结果也表明预测样本输入参数在学习样本参数附近时，模型识别率都很理想，最高达到100%。