封闭气体压强计算归类分析

谢汝成

(吉林省辽源市第五中学 136200)

纵观近几年高考在选修部分的考察，选修3-3部分与初中知识衔接紧密，高考题目难度相对稳定，对比3-4得分相对容易，所以越来越多的一线教师和学生在备考时都将选修部分复习的重点落在了3-3部分.在选修3-3部分中气体的相关状态参量的计算一般以10分的计算题形式呈现.压强作为描述气体的状态参量之一，往往是解决问题的关键，所以封闭气体压强的计算是教学重点但同时也是学生学习的难点.为了帮助学生突破这一难点，我对这一类问题进行了相应的归纳总结，在此和同仁探讨.

从密封方式分析，通常有两种“液封”和“固封”.从封闭气体所在系统所处于的力学状态分析，通常也有两种“平衡系统”和“加速系统”. 下面我们就对具体的问题进行归类分析：

一、平衡类

处理此类问题首先要选择合适的研究对象(一般为用来封闭气体的液体、活塞等)，结合帕斯卡定理和连通器原理对研究对象进行受力分析，列平衡方程求解.

1.直型管

此类问题选择某一段或几段水银柱为研究对象列平衡方程.其中液体柱压强p=ρgh，带入相应数据，可求得帕斯卡单位下的压强数值.而在高中阶段通常以水银柱为例考察，此时液体柱压强可以表示为p=hcmHg.

(1)试计算下述几种静止情况下各封闭气体的压强，已知大气压强P0=76cmHg，管中每段水银柱的长度均为10cm.

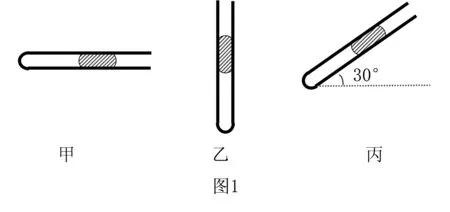
解析

图1甲以水银柱为研究对象：ps=p0s，可解，p=p0=76cmHg

图1乙以水银柱为研究对象：

ps=p0s+ρghs，可得p=p0+ρgh=(76+10)cmHg=86cmHg

图1丙以水银柱为研究对象：

ps=p0s+ρghssin30°

(2)如图2所示，在装满水银的槽内有一个体积非常小的气泡，气泡距水银液面10cm，已知大气压强P0=76cmHg，求气泡内气体压强

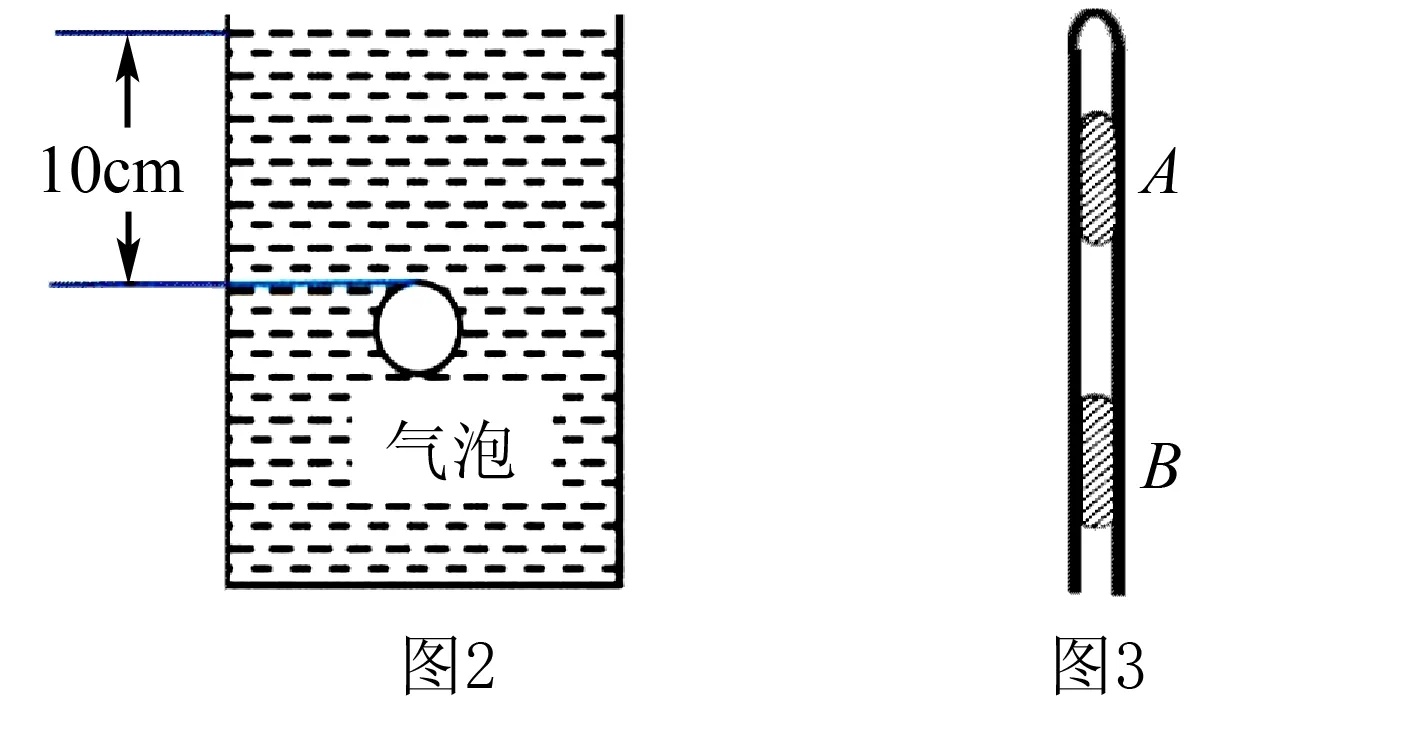
解析取气泡上方横截面积为s高为10cm的水银柱，列平衡方程

ps=p0s+ρghs，可得p=p0+ρgh=86cmHg

注：也可直接分析，气泡内压强来源于大气和10cm高水银柱压强之和

p=p0+ρgh=86cmHg

(3)如图3所示，已知大气压P0=76cmHg，水银的密度为ρ，管中两段水银柱的长度均为10cm，求上下两段封闭气体的压强P1和P2

解析以B段水银柱为研究对象，列平衡方程

p0s=p2s+ρghs，可得p2=p0-ρgh=66cmHg

以A段水银柱为研究对象.列平衡方程

p2s=p1s+ρghs，可得p1=p2-ρgh=56cmHg

注：在计算上端气体压强p1时，也可以以AB两段水银柱和下端封闭气体这一整体为研究对象.此时有p0s=p1s+2ρghs，可得p1=p0-2ρgh=56cmHg.

解决直型管平衡类问题时，通常以某一段水银柱(若题中未直接给出水银柱，可在系统中“构建”一个水银柱，如题2)为研究对象，通过对其两侧气体压力和重力的分析，列取力学平衡方程，代入相应数据并计算.多段水银柱封闭多段气体时，通常情况下分析的顺序为，先对与大气相接触那部分水银柱为研究对象，求出第一段封闭气体的压强，再逐级分析.也可以将所有水银柱视为一个整体分析出最边缘一部分封闭气体的压强，再逐个分析.

2.U形管

在U形管类问题中，关键的问题在于解决左右两侧不同位置的压强关系.即同一种连续不间断的液体在同一水平面上的压强相等.此类问题通常以两侧“液面差”那一部分水银柱为研究对象，列方程求解.

(4)如图4甲所示，竖直放置的U形管，左端开口右端封闭，左右两测液面差为10cm，已知P0=76cmHg，求右侧封闭气体的压强

解析在右侧管中选取与左侧液面A点等高的B点，由连通器原理可知AB两点压强相等.选取以右侧高出左侧的10cm水银柱为研究对象，设水银柱横截面积为s，受力分析如图4乙所示，列平衡方程

p0s=ps+ρghs，可得p=p0-ρgh=66cmHg

(5)如图5甲所示，直管插入水银槽内，管内水银液面比槽内液面高10cm，已知P0=76cmHg，求管内封闭气体的压强.

解析本题实际上是一个U形管问题，点睛之笔找出等效的连通部分构建出一个液面以下的U形管如图5乙所示，由此可知解法同上题一致

p0s=ps+ρghs，可得p=p0-ρgh=66cmHg

注：如图5丙所示，若管内液面低于水银槽液面，选槽外横截面积为s的高为10cm水银柱为研究对象，则有

ps=p0s+ρghs，可得p=p0+ρgh=86cmHg

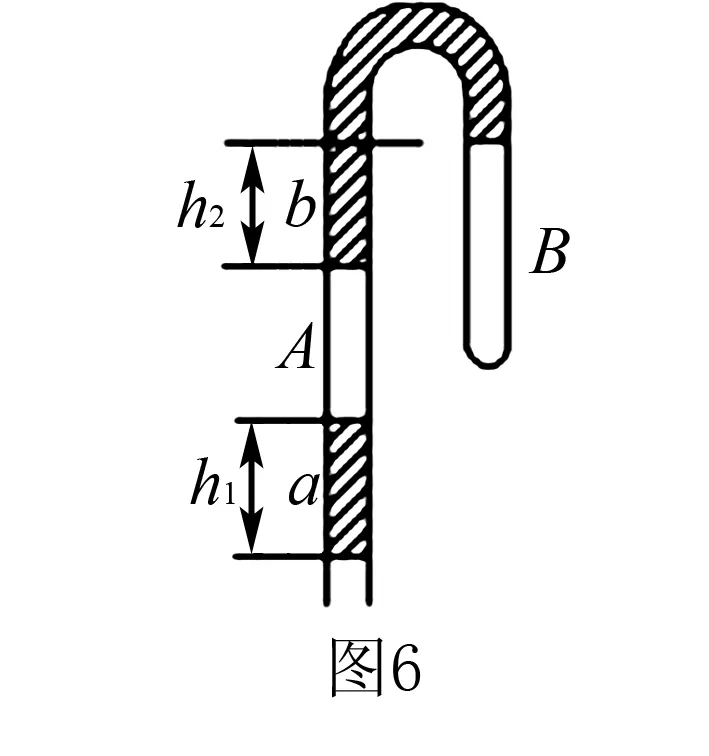
(6)如图6所示，竖直放置的U形管，左端开口右端封闭，水银柱a、b将A、B两段空气柱封闭在管内．已知水银柱h1=h2=10 cm，大气压强P0=76cmHg，求空气柱A、B的压强.

解析以a水银柱为研究对象，设水银柱横截面积为s，列平衡方程

p0s=pAs+ρgh1s，可得pA=p0-ρgh1=66cmHg

以b段水银柱中左右两侧液面差h2段为研究对象，列方程可得

pAs=pBs+ρgh2s，可得pB=pA-ρgh2=56cmHg

在U形管类问题中，关键的问题在于借助连通器相关知识分析求解左右两侧液体中不同位置的压强关系.我们首先需要找出题目中直接或间接存在的“连通器”，再以两侧液面多出部分的水银柱(如例4中B点上方水银柱和例5中比槽内液面高出的10cm水银柱)为研究对象，分析水银柱两侧受到的压力和自身重力，列受力平衡方程求解.

3.汽缸活塞

汽缸活塞类问题一般情况下解法不唯一，选择的研究对象可以是汽缸或活塞，也可以是汽缸和活塞的整体，不同的研究对象对应不同的受力情形，多数情况下选择受力个数较少或受力情况简单的物体为研究对象.

(7)用细线将汽缸悬挂在天花板上,如图7所示,汽缸筒的质量为M,活塞质量为m,活塞面积为S，大气压强为P0,求汽缸内气体的压强.(忽略活塞和汽缸间摩擦)

解析以汽缸为研究对象，列平衡方程

注：本题亦可以活塞为研究对象，其中利用整体法可求绳对活塞拉力T=(M+m)g，列方程可求答案.

(8)一汽缸静置于地面上,如图8甲所示,活塞质量为m,活塞底面积为s斜面倾角为θ,大气压强为p0,求汽缸内气体的压强p.(忽略摩擦)

以活塞为研究对象，活塞处于受力平衡状态，作出受力分析图，如图8乙，列竖直方向平衡方程

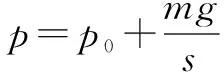
注：由大气对活塞竖直分量p0scosθ=p0s可以看出，大气向下的压力只与活塞面积的水平分量有关，与斜面倾角无关，即该类问题与活塞的上下表面形状无关.

(9)如图9所示，两端开口的汽缸水平固定，A、B是两个厚度不计的活塞，面积分别为S1=20 cm2，S2=10 cm2，它们之间用一根细杆连接，B通过水平细绳绕过光滑的定滑轮与质量为M的重物C连接，静止时重物C的质量M=3 kg，已知大气压强P0=1×105Pa，取g=10 m/s2，(缸内气体可看作理想气体，不计一切摩擦).求：汽缸中的气体压强P.

解析以两活塞整体为研究对象，杆中弹力对两活塞等大反向，对整体的受力无影响.由于两活塞面积不等，封闭气体对两活塞的压力满足PS1>PS2，封闭气体对活塞整体有力的作用.列平衡方程

PS1+P0S2=P0S1+PS2+Mg

代入数据可得：P=1.3×105Pa

注：本题也可单独分析两个活塞的受力平衡状态，设出杆对两活塞力的方向，分别列取关于两个活塞的平衡方程，消去杆中力，即可求解出封闭气体压强.

注:汽缸活塞类问题一般情况下解法不唯一，选择的研究对象可以是汽缸或活塞，也可以是汽缸和活塞的整体，不同的研究对象对应不同的受力情形.多数情况下，单个活塞问题使用隔离法，选择受力个数较少或受力情况简单的物体(活塞或汽缸)为研究对象，可以避免分析不必要的外力.双活塞问题时使用整体法，选择两个活塞构成的整体为研究对象.可以避免分析连接两活塞的绳或杆中的力，但应重点注意内力(封闭气体对活塞的压力之和)是否为零.在(7)的求解过程中，大部分学生借用以往经验直接按内力为零处理，而未考虑两活塞受力面积不等，这是造成此类问题失分的最大陷阱.

二、加速类

(10)如图10甲所示，有一段长L=12cm的水银柱，在均匀玻璃管中封住一定质量的气体，若开口向上将玻璃管放置在倾角为θ=30°的光滑斜面上，大气压强P0=76cmHg,g=10 m/s2.求下滑的过程中被封住气体的压强P.

解析水银柱与玻璃管一起沿光滑斜面匀加速下滑，可以看成连接体问题.分析这一整体

可得，a=gsin30°

再以水银柱为研究对象，画出受力分析图，如图10乙所示，沿斜面方向列牛顿第二定律方程，设水银柱横截面积为S

P0S+mgsinθ-PS=ma,其中m=ρLs

代入数据可得P=P0=76cmHg

注：本题中斜面光滑，水银柱的重力沿斜面分量全部用来产生加速度，对封闭气体压强无贡献，同理将玻璃管开口沿斜面向下，气体压强不变.

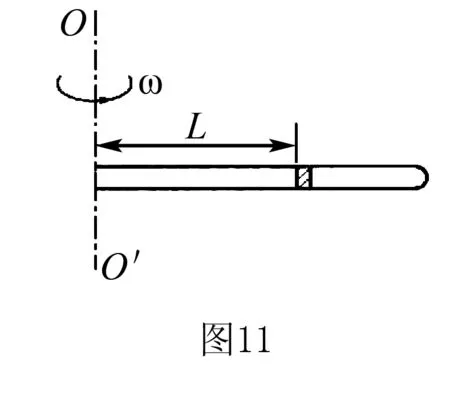
(11)如图11所示,粗细均匀的玻璃内有一横截面积为S质量为m的活塞，活塞封闭了一段气体.现使试管在水平面内以角速度ω绕轴OO′匀速转动,此时活塞和转轴的距离为L.活塞不漏气且不考虑摩擦和温度的变化,大气压强为P0.求此时封闭气体的压强为P.

解析活塞绕轴做匀速圆周运动，其所受合力充当向心力,列向心力方程

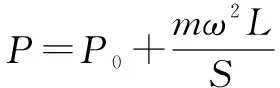
(12)如图12所示.粗细均匀的U形细管水平部分长为L,管中盛有一定质量的液体,当U形管以加速度a向右运动时,求两管中液面的高度差Δh.

解析以管中水平部分水银柱为研究对象，U形管中水平该部分左右两端受到竖直水银柱的压力，设管中右侧水银柱高为H,大气压强为P0，则

左端受到向右的力F左=P0S+ρg(H+Δh)S

右侧受到向左的力F右=P0S+ρgHS

水平水银柱质量m=ρLS

列牛顿第二定理

F左-F右=[0S+ρg(H+Δh)S]-[P0S+ρgHS]=ma

加速类问题比平衡类问题复杂，首先应通过分析确定研究对象(与气体相关的活塞或水银柱)，确定加速度(合外力)的方向，确定研究对象受力情况(特别注意分析气体对各部分的压力区别)，最后列牛顿第二定律求解.

封闭气体压强的计算，是分析求解理想气体状态方程类问题的关键步骤.计算封闭气体问题是一般遵循以下几个步骤，

1.确定适当的研究对象.封闭结构简单的问题一般选择隔离分析活塞、缸体或液柱，受力较为简单，易于求解.封闭结构复杂的问题一般选择整体法，此时可以有效地避免分析复杂的内力.

2.分析研究对象受力.隔离分析时，应注意分析研究对象的重力.整体分析时，应重点注意内力(封闭气体对活塞的压力之和)是否为零.

3.列方程求解.在选择合适的研究对象后，根据研究对象所处的力学状态，列出相应的力学平衡方程或牛顿第二定律方程，即可代入数据进行相应的求解.