一道校级竞赛选拔题的解答与思考

郑 良

(安徽省合肥市第四中学 230000)

一、试题呈现与解答

题目设x,y,z为整数，且x+y+z=3，x3+y3+z3=3，则x2+y2+z2=____.

解法1设x=1+a，y=1+b，z=1+c，由x+y+z=3中，得a+b+c=0，代入x3+y3+z3=3，得a3+b3+c3+3(a2+b2+c2)=0.因为a3+b3+c3-3abc=(a+b+c)(a2+b2+c2-ab-bc-ca)=0，所以a3+b3+c3-3abc=0.所以a2+b2+c2=-abc，且abc≤0.

所以x2+y2+z2=a2+b2+c2+2(a+b+c)+3=a2+b2+c2+3=3-abc.

(1)若a,b,c中存在数为零时，可得a=b=c=0，那么x2+y2+z2=3，此时x=y=z=1满足条件；

(2)若a,b,c中不存在数为零时，由abc≤0可知它们为两正一负，不妨设a≥b>0>c.

将c=-a-b代入a2+b2+c2=-abc，得2(a2+ab+b2)=ab(a+b).

当ab=2，a+b=2时，方程组无解；

当a+b=6，ab=9时，a=3，b=3，此时c=-6，即x=4,y=4,z=-5，所以x2+y2+z2=57.

综上所述，x2+y2+z2的值为3和57.

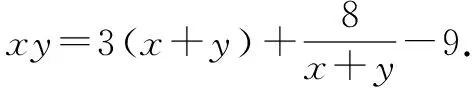
分别解得x=y=1，无解，x=y=4.

当x=y=1时，z=3-(x+y)=1，x2+y2+z2=3；

当x=y=4时，z=3-(x+y)=-5，x2+y2+z2=57.

综上所述，x2+y2+z2的值为3和57.

解法3不妨设x≥y≥z，由x+y+z=3，得x≥1，z≤1，所以x+y=3-z≥2.

由x+y=3-z，得x3+y3=3-z3.

因为x+y|x3+y3，即3-z|3-z3.

(1)当3-z=2，即z=1时，x+y=2，x3+y3=2，得x=y=1，此时x2+y2+z2=3；

(2)当3-z=3，即z=0时，x+y=3，x3+y3=3，方程组无实数解；

(3)当3-z=4，即z=-1时，x+y=4，x3+y3=4，方程组无实数解；

(4)当3-z=6，即z=-3时，x+y=6，x3+y3=30，方程组无实数解；

(5)当3-z=8，即z=-5时，x+y=8，x3+y3=128，得x=y=4，此时x2+y2+z2=57；

(6)当3-z=12，即z=-9时，x+y=12，x3+y3=732，方程组无整数解；

(7)当3-z=24，即z=-21时，x+y=24，x3+y3=9264，方程组无整数解.

综上所述，x2+y2+z2的值为3和57.

目前太谷县全县50%饮用水来源于庞庄水库，庞庄水库主要向两个水厂（站）供水，分别是太谷县自来水公司在杨家庄村设立的水厂和小白供水站。主要用水区域为太谷县城、小白乡、水秀乡、胡村镇。

解法4令d=y+z，e=z+x，f=x+y，则d+e+f=6，d,e,f均为整数，不妨设f最大，故f≥2.

3def=3(x+y)(y+z)(z+x)=(x+y+z)3-(x3+y3+z3)=24，所以def=8.

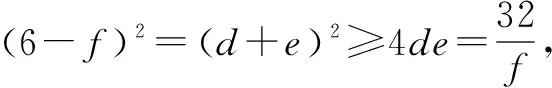
得(f-2)2(f-8)≥0.

当f=2时，则d+e=4，de=4.解得d=e=f=2.即x=y=z=1，此时x2+y2+z2=3；

当f≠2，则f≥8.又def=8，d,e,f均为整数，故f=8，则d+e=-2，de=1，解得d=e=-1，即x=y=4，z=-5，此时x2+y2+z2=57.

综上所述，x2+y2+z2的值为3和57.

评注解法1从增量的角度设元，从而将x,y,z的关系转化为a,b,c的关系，构建目标x2+y2+z2与a,b,c的联系，再结合a+b+c=0和abc≤0，利用符号法则进行分类讨论，对于“a,b,c中没有数为零时”，通过变形利用整数的分解进行转化，无论哪种情况，都要验证所求值的存在性.

解法2直接联立消去z，构建xy与x+y的关系，利用整数的性质及数的整除性化无限为有限，求解关于x、y的方程组，最终确定目标.当然也可将3(x+y)2-(xy+9)(x+y)+8=0视为关于x+y的一元二次方程，根据(xy+9)2-96为完全平方数求解.

解法3从x+y与x3+y3之间的关系入手，利用整除的性质得到3-z|24，进而求解关于x，y的方程组，最终确定目标.

解法4根据已知条件巧妙换元，利用公式3(x+y)(y+z)(z+x)=(x+y+z)3-(x3+y3+z3)实施化归，进而构建不等式进行消元，等价变形是解题的关键.

二、两点思考

1.注重逻辑推理过程，确保过程与结果的正确性

很多学生通过观察，发现x=y=z=1是满足条件的一组解，直接得出“结果x2+y2+z2=3”.事实上，x=y=z=1只是满足条件的局部解，是否是唯一解并未加以证实，岂能用特殊代替一般.以上解答中，根据对称性均对实数x,y,z进行了排序，从而利用平均值原理简化求解过程，通过以上过程可知满足条件的解(x,y,z)为四组，分别为(1,1,1)，(4,4,-5)，(4,-5,4)，(-5,4,4).平时学习时，我们要加强推理，逐步形成严谨有序的推理习惯，积累规范表达的基本技能.

2.理解与掌握“四基”，提高解题的合理性与灵活性