基于短时交通流量预测对路网微观交通仿真的研究

张 虎

（苏州高等职业技术学校 机电工程系，江苏 苏州 215009）

利用各种预测模型和方法对获取的实时交通信息进行准确的预测，在短时交通流量预测的基础上，提出将预测数值导入到VISSIM路网微观交通仿真中，根据下一阶段交通流量调整信号时长，为信号系统控制方案的变更提供参考依据。

1 短时交通流量预测现状分析

短时交通流量预测是根据路段及相关路段在过去p个时刻的交通流量参数值f(t-k)(k=1，2，…，p)，利用合适的预测模型和方法，处理各种检测器采集到的实时交通数据，从而求出该路段未来k个时间段内的交通流量状态估计值f(t-k)[1]。

时间序列模型[2]，卡尔曼（Kalman）滤波[3]和人工神经网络模型[4]是三种传统预测模型。这三种传统预测模型主要存在以下问题：①在预测时长和预测精度上不能做到很好的统一，现阶段很难运用到实时的在线预测中。②在短时交通流量预测时间间隔的选取上差异较大。③在预测时间段上并没有很好地与道路的实际应用结合，为了追求预测精度，在大样本数据的基础上，大多数模型是对全天的交通流量进行预测，甚至有的模型针对路段车流量稀少的凌晨进行预测，忽视了路段的实际情况。

针对第一个问题，近年来很多学者采用了一些新的预测方法来对短时交通流量进行预测，如蚁群算法[5]，贝叶斯网络多方法组合[6]和深度学习[7]等。针对第二个问题，提出短时间交通流量预测的时间间隔为5 min，如何在5 min内准确地完成交通流量预测是实现交通控制与诱导的关键[8]。针对第三个问题，对易导致交通拥堵的早高峰短时交通流量进行预测。

灰色预测模型以其算法简单，所需数据少，运算时间短的优点受到智能交通研究人员的青睐。2006年，邓志龙等[9]建立了GM（1，1）滚动预测模型。2012年，吴宝春等[10]提出基于遗传灰色GM(1，1，ρ)模型的短时交通流量预测。传统预测模型对于基础数据的依赖程度相当高，需要大量基础数据，很大程度上制约了这些方法的应用。而GM预测模型能够用现实当中少量数据进行建模，恰好克服了需要大量基础数据的制约，得出相对满意的结论。GM预测模型的优势，符合早高峰短时交通流量分时段预测的需求。且GM预测模型具有响应时间较快的优势，能很好地运用到实时在线预测。在对一系列的交通流量的短时预测算法进行比较后，对灰色GM(2，1)模型做出了改进，提出CPSO–GM(2，1，λ，ρ)模型对短时交通流量进行滚动预测。

2 CPSO–GM(2，1，λ，ρ)组合预测模型

2.1 灰色GM(2，1，λ，ρ)预测模型

灰色GM（2，1）预测模型有2个特征值，可以反映单调或振荡的情形，但在实际建模过程中发现其预测精度偏低。刘虹等[11]提出了将灰色GM(2，1)预测模型的向前、向后差分进行线性组合出灰色GM(2，1，λ，ρ)模型，利用参数λ修正背景值；然后引入参数ρ对原始数列进行数乘变换，进一步将模型拓展为灰色GM(2，1，λ，ρ)预测模型。

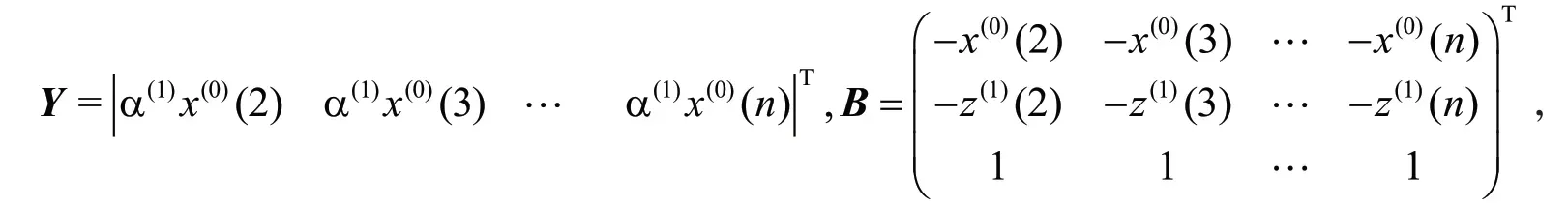
其 中 ：序 列X(1)的 紧 邻生成序列Z(1)定 义 为，将式(1)微分方程离散成向前、向后的差分，由于时间序列中，故有用λ对向前、向后差分进行线性组合得新背景值为：

使用数乘参数ρ对原始数列进行数乘变换，将原来的病态矩阵转化为良态，得GM(2，1，λ，ρ)模型。可得。当λ=0.5，ρ=1时，GM(2，1，λ，ρ)模型即为普通灰色GM(2，1)模型。

2.2 PSO算法简介

PSO初始化为一群随机粒子(随机解)。然后通过迭代找到最优解。在每一次的迭代中，粒子通过跟踪两个“极值”(pid，p gd)来更新自己[12]。在找到这两个最优值后，粒子通过式（2）和式（3）来更新自己的速度和位置。

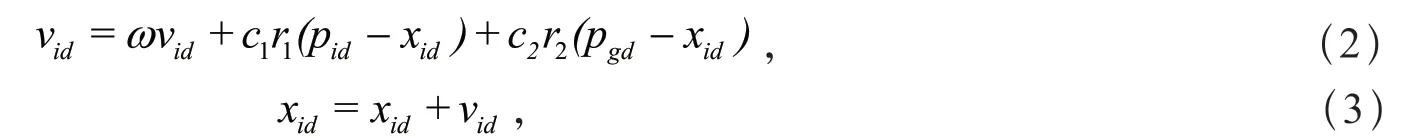
其中:ω为惯性权值(inertia weight);c1和c2为正常数，称为加速系数(acceleration coefficient);r1和r2是两个在[0，1]范围内变化的随机数;pid为个体极值;pgd为全局极值。

2.3 CPSO－GM(2，1，λ，ρ)模型算法流程

在利用CPSO对GM(2，1，λ，ρ)模型优化的过程中，建立由λ，ρ构成一个二维的微粒群微粒，以平均百分比误差作为适应度函数，以其值最小为目标，寻求最优解，构成CPSO–GM(2，1，λ，ρ)模型。该模型算法流程如图1所示。

Step 1:初始化粒子速度、位置等相关参数。按照群体规模M生成初始化群体(λρ)。设定微粒的初始位置和初始速度。

Step 2:调用交通流量的原始数据，计算粒子群的适应值。

1）目标函数：取平均百分比误差为适应度函数，以其值最小为目标进行优化。

2）计算粒子群的适应度，并从M个初始群体中选取性能较好的N个作为初始解，随机产生N个初始速度。

Step 3:如果适应度达到精度或者迭代次数大于Gen，则执行步骤Step 8；如果适应度未达到精度或迭代次数不满足条件，则执行Step 4。

Step 4:更新个体极值和全局极值，判断是否早熟。如果是早熟，则Logistic混沌优化搜索；如果未早熟，则执行Step5。根据Logistic方程得到n个向量为目标函数中的变量个数，将Zi的各个分量载波到对应变量的取值区间。

Step 5:根据式(2)和式(3)，计算各微粒新的速度和新的位置。

Step 6:与当前搜索的最优值比较。对于每个微粒，比较其当前适应度值和其个体历史最好适应值，如果，则；比较群体所有微粒的当前适应度值和全局历史最好适应度，如果，则

Step 7:保存本次迭代寻优结果。检查更新数据后的粒子适应度是否达到标准，如果达到标准，则保存此次迭代寻优结果，并执行Step 3。

图1 CPSO-GM(2,1,λ,ρ)预测模型算法流程图

Step 8:输出最优参数λ∗和ρ∗，输出预测短时交通流量、平均百分比误差。

3 短时交通流量滚动预测实验仿真

为进一步提高预测精度与实时性，在采用模型预测过程中，预测数据与交通管制中心的数据库应保持同步，用实测值代替预测值，预测值不参加下一次的预测，以减少误差的累积，可进一步提高预测精度。滚动周期T的取值应能够反应时间序列的变化趋势，采用的游程法对不同滚动周期T下的残差序列进行计算，当周期T=12时，三天残差序列的均值最优，故选取T=12作为滚动周期值。因此，选取案例路段每天早7:00～9:00的12个基础数据将作为训练数据用于建模。结合短时交通流量分时段研究，对案例路段早高峰短时车流量进行预测。

CPSO主要参数设置为µ=4，微粒维数n=2，种群大小M=100，加速系数c1=c2=2，ω=0.729，最大迭代数为1 500。第一天早高峰单步数据拟合曲线图如图2所示。由图2可知，预测模型能很好地拟合所研究路段早高峰交通流量的走势，较准确地预测出下个5 min的交通流量。CPSO–GM(2，1，λ，ρ)预测结果与实际值对比见表1，由表1可知，三天早高峰预测的平均百分比误差分别为2.77%、4.03%、3.36%，预测模型能够较好地预测案例路段早高峰的短时交通流量。

图2 第一天早高峰单步数据拟合曲线图

在预测到交通流量（一般时间间隔5 min）后，根据车流量与道路的关系建立相应的交通状态判别标准，赋予实测值和预测值不同权重判断路段下各时刻的交通状态，从而实现交通诱导的功能。在5 min内，所预测路段可以建立如下标准：①交通流量＜140时，认为该路段畅通；②140≤交通流量＜150时，认为该路段车辆行驶缓慢；③交通流量≤150时，则认为该路段会发生交通拥堵。据此可向出行者提前提供一些重要路段的动态路况信息，提前采取规避措施，降低交通拥堵的发生概率，提高道路的通行效率。

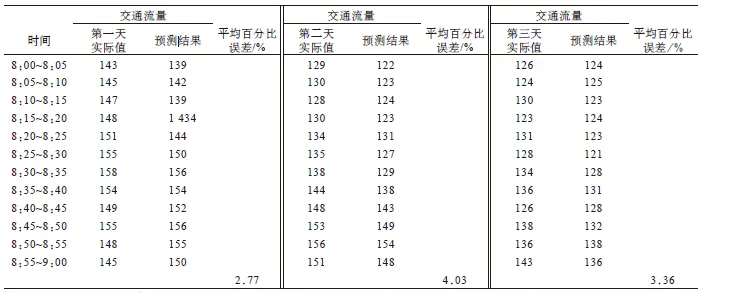
表1 CPSO-GM(2,1,λ,ρ)预测结果与实际值对比

4 VISSIM路网仿真

基于VISSIM对交通的微观仿真国内学者做了很多的研究[12]，VISSIM是目前我国交通应用最广泛的微观仿真模型。不同于对某个路口的仿真，对路网的仿真则呈现为调查量较大，工作繁重且较为细致。通过各种渠道获取路网仿真的基本数据，如：路段名称、车道宽度、交叉口、出入口的位置及间距，信号控制特点。其中信号控制特点包括：信号配时、绿信比、是否有左转信号灯、饱和流量及理论行程时间等。

VISSIM提供了多种类型的评价功能，且可选取不同的时间段进行评价，运行仿真路网是选取600～1 200 s的数据进行评价。依据行程时间仿真评价结果，选取的测试路段行程时间仿真值与实际值比较误差在允许范围之内，由此可认定所构造的路网符合实际情况，达到了路网仿真的预期要求。VISSIM使用两个基本的组件(Link和Connect Links )来描述一条连续的路径，进而描述整个路网。

构建VISSIM–Excel VBA–Matlab平台，实现了VISSIM、Excel VBA、Matlab的交互，使得VISSIM中的当前交通流量通过Excel VBA传入Matlab，Matlab在调用当前交通流量做出预测后，再将预测值通过Excel VBA传入VISSIM的交互过程。

建立VISSIM–Excel VBA–Matlab平台，实现路网微观交通仿真和交通流量预测数据的交互之后，将预测值输入到Excel VBA中，信号优化控制模块根据预测值设置新的方案，通过Excel VBA导入VISSIM进行仿真，比对前后延误数据，据此评价信号控制方案改进前后的优劣。主要步骤：①将当前交通流量输入VISSIM进行微观路网仿真；②将当前流量传入Excel VBA；③Excel VBA把数值导入Matlab；④调用短时交通流量预测模块，预测下个阶段的短时交通流量；⑤将预测值传入Excel VBA；⑥信号优化控制模块根据预测值设置新的方案；⑦Excel VBA将调整后的配时方案传入VISSIM；⑧VISSIM进行微观路网仿真，通过判断延误数值确定控制方案的优劣。

5 结论

1）针对粒子群算法容易陷入局部极值点的问题，将Logistic混沌搜索嵌入到PSO算法，应用混沌粒子群算法（CPSO）寻找灰色GM(2，1，λ，ρ)预测模型最优的参数λ和ρ。构建了CPSO–GM(2，1，λ，ρ)短时间交通流量预测模型。运用Matlab编程实现CPSO–GM(2，1，λ，ρ)模型对三天早高峰短时交通流量滚动预测。模型对工作日的早高峰（8:00～9:00）短时交通流量进行预测，在5 min时间波动内的误差总量不超过10辆车，达到了90%的目标准确率，从而为交通流量的短时预测提供了一种有效的方法。

2）将预测的短时交通流量和VISSIM相结合，实现了短时交通流量预测和路网仿真协同控制，得出了优于固定信号配时的信号控制方案。VISSIM具有可靠的微观交通仿真能力，Excel VBA对数据的处理和通信能力较强，Matlab可以实现复杂的交通控制算法，三者相互结合构建的仿真平台模拟出来的实验环境与真实的交通运行状况还有一定的差距，但已经有了很大的提高。短时交通流量和路网仿真的结合也为城市交通控制方案的设计提供了新的路径。