钝锥表面脉动压力风洞试验研究

（中国工程物理研究院总体工程研究所，四川 绵阳 621999）

飞行器高速再入时，除了经历极其严酷的过载与热环境外，边界层内空气的无序运动也会造成极强的噪声环境，伴随着的是作用于飞行器表面的脉动压力载荷。由于脉动压力频域特性分布较宽，可能激发飞行器各阶振动响应，导致内部产品功能失效，甚至结构破坏。脉动压力是飞行器振动环境载荷预示以及结构设计的重要依据。此外，飞行器再入时的内噪声环境也主要是由脉动压力引起的。因此，脉动压力环境的研究与预测，对飞行器载荷环境预示及结构设计具有极其重要的意义。

目前，研究飞行器脉动压力的主要手段包括经验公式、数值模拟、风洞试验以及飞行试验。对于经验公式法，自20 世纪60 年代以来，开展了一系列试验和研究以理解和预测脉动压力[1-10]。徐立功[11]总结了一套预测各种场景下脉动压力环境统计特性的工程计算公式，包括均方根脉动压力、功率谱密度和交叉功率谱密度值，在国内应用较为广泛[12-14]。上述经验公式主要针对湍流边界层状态，对于转捩过程脉动压力的变化情况以及频率特性，给出明确拟合公式的文献相对较少。随着高性能计算机的兴起，直接数值模拟（Direct Numerical Simulation-DNS）应用于对超声速圆锥的边界层模拟。Sivabramanian 等[15-16]对超声速下的圆锥局部扰动诱导的转捩进行了研究，指出边界层内存在基波共振与亚谐波共振2 种非线性作用机制。李新亮[17]针对尖锥开展了零攻角以及小攻角下的直接数值模拟，发现了在转捩位置前存在着非常低频的脉动压力，这可能是由第一或者第二模态引起。目前，数值模拟主要针对转捩过程及机理进行研究，对脉动压力频率特性特别是对结构影响比较大的低频段研究相对较少。在风洞实验方面，国内外也开展了较多的研究。刘向宏[18]按照边界层自然转捩的发展过程，回顾了国内外在边界层感受性问题以及线性化阶段风洞试验研究的现状，并总结了风洞试验在未来超声速边界层转捩研究中的工作与意义。从总结的情况来看，大部分风洞试验结果中脉动压力侧重于高频（106Hz 量级）的测量与分析，研究方向仍然以流动机理为主，对低频段关注相对较少。对于飞行试验，美国空军研究实验室（Air Force Research Laboratory-AFRL）与澳大利亚国防科学技术组织（Defence Science and Technology Organization-DSTO）联合开展了名为HIFiRE（hypersonic International Flight Research Experimentation）的超声速飞行试验计划，该计划准备通过10 年、9 次超声速飞行试验以发展超声速可持续飞行技术。其中，HIFiRE1 与HIFiRE5针对边界层转捩现象进行了试验测量，获得了飞行过程中圆锥及椭圆锥构型的表面脉动压力数据[19]。飞行试验可测量真实飞行工况下的脉动压力数据，但受限于飞行状态不易控制以及测量手段，飞行试验过程中能获得的脉动压力信息十分有限，并且试验周期长，资源消耗大。

圆锥模型由于构型简单、反应三维流动特性以及国防需求背景强烈等因素，被作为标模广泛应用于数值模拟、风洞试验以及飞行试验研究中，用于脉动压力的分析与预测。文中以钝锥模型为研究对象，利用风洞试验对模型表面脉动压力进行测量，获得脉动压力载荷时域、频域特征随来流雷诺数变化的规律，为飞行器再入环境脉动压力预示提供试验数据支撑。

1 试验风洞

试验在中国航天空气动力技术研究院的超声速风洞FD-07 中进行。该风洞口径为φ0.5 m，试验段尺寸为1880 mm×1400 mm×1130 mm，侧壁伴有口径为φ350 mm 的光学玻璃窗口。该风洞工作介质为空气，名义马赫数范围为4～10，如图1 所示。

图1 FD-07 风洞Fig.1 FD-07 wind tunnel

2 模型与设备

2.1 试验模型

试验模型材质为45#钢，头部为钝头体的圆锥。沿外形子午线轴向设置了4 个测点，分别位于0.29、0.64、0.74、0.84 倍钝锥轴向特征长度处，用于进行试验过程中的脉动压力测量。在各测点位置安装了脉动压力传感器，传感器表面与试验模型表面尽可能保持平齐或略微下沉。

2.2 试验仪器与设备

该脉动压力试验在FD-07 风洞试验段进行。通过连续改变试验段运行总压，实现气流密度的改变，进而实现设计的雷诺数连续变化工况。该实验压力传感器型号为KulitteXCQ-100-25B 绝压传感器，量程为0～25 PSI，固有频率为240 kHz，灵敏度和线性误差为满量程输出（FSO）的±0.1%。传感器直径为2.6 mm，压力传感器外包覆聚四氟乙烯套以实现绝缘，安装时传感器、聚四氟乙烯套端面与钝锥表面平齐。

采用江苏东华DH3840 信号调理仪（放大器）为Kulitte 传感器进行供电，并对输出信号进行100 倍增益放大，频带宽度为DC～300 kHz（+0.5～-3 dB）。采用成都华太LXI-5402 16/500K 数据采集器对脉动压力数据进行采集，采样频率为50 kHz，分辨率为16 bit。由于试验过程中来流参数随时间是变化的，数据采集系统从试验开始对压力数据进行全程采集，采样时间约为60 s。

3 结果与分析

通过连续改变总压实现雷诺数连续变化进行钝锥表面脉动压力的测量。本试验条件为Ma=6、α=0°，单位长度雷诺数变化范围为4.5×107～1.0×107m-1，试验实施时雷诺数由高到低变化，变化曲线如图 2所示。

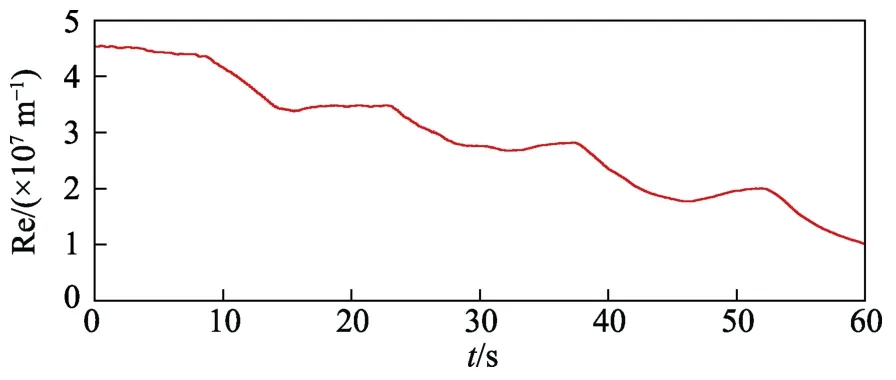
图2 试验过程雷诺数变化情况Fig.2 The Reynolds number variable during the test

钝锥表面不同位置压力随时间的变化曲线如图3所示。可以看出，随着雷诺数降低，脉动压力信号从钝锥端头至底部，依次呈现由“喧闹”突然变为“安静”现象。

图3 不同位置脉动压力随时间变化曲线Fig.3 The surface fluctuations of different locations with time

上述测点利用自由来流动压进行归一化的脉动压力随时间变化曲线（采用10kHz 低通滤波）如图4所示。对于x/L=0.29 测点，由于测点靠前，当地雷诺数较小，归一化脉动压力时域信号幅值在12 s 左右略微变小，但变化不明显。对于x/L=0.64、0.74、0.84测点，12 s 之前，压力系数幅值较为稳定，12 s 后开始呈现出幅值放大的趋势，25 s 左右幅值达到最大状态，40 s 后幅值又开始减小。40 s 以后，个别测点压力系数又呈现出变大的趋势，这可能是由于边界层变为层流后，背景噪声占比变大引起的。图5 中的归一化脉动压力均方根值（采用10 kHz 低通滤波）也同样反映出该变化趋势。从图5 中还可以看出，转捩过程中的钝锥表面归一化脉动压力均方根值最大值约为湍流的2 倍。

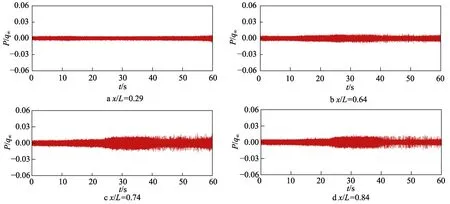
图4 不同位置归一化脉动压力随时间变化曲线Fig.4 The normalized surface fluctuations of different locations with time

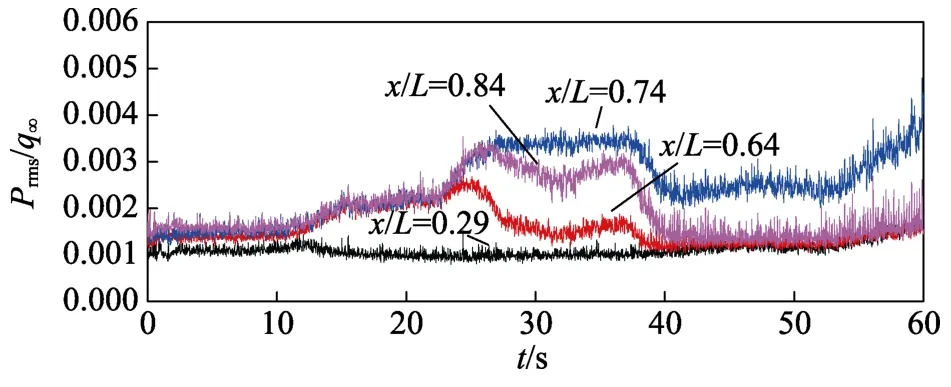
图5 归一化脉动压力均方根值随时间变化规律Fig.5 The normalized surface fluctuation root mean square of different locations with time

对各测点压力时域信号利用自由来流动压归一化后进行傅里叶变换，采用Welch[20]的方法对脉动压力信号进行时频变换，计算功率谱密度（PSD），计算窗口为1 s。为了减小数据处理过程中的谱泄漏和旁瓣效应的影响，选取Hanning 窗函数进行数据加窗处理，窗口大小为8192 个数据点，窗口重叠率为 50%，功率谱密度函数估计的频率f分辨率为6.1 Hz。各测点在不同时刻的归一化功率谱密度如图6—9 所示。

图6 x/L=0.29 处不同时刻归一化脉动压力功率谱密度Fig.6 The normalized surface pressure fluctuation PSD at x/L=0.29 of different time

对于x/L=0.29 测点，由于位置较为靠前，当地雷诺数较小，并且风洞背景噪声较大，10 Hz～10 kHz间功率谱密度变化不明显。对于x/L=0.64、0.74、0.84等3 个测点，在0～10 s 过程中，边界层为湍流状态，归一化功率谱密度频率特性保持不变。10～30 s 过程中，随着雷诺数从高到低，边界层由湍流状态逐渐进入转捩状态，6 kHz 附近频段脉动压力功率谱密度优先开始增长，随后扩展至整个低频段。30～40 s 过程中，边界层由转捩状态逐渐进入层流状态。可能是由于背景噪声的缘故，出现了层流状态的归一化脉动压力功率谱密度整体较湍流状态高的现象。圆锥类再入飞行器实际再入过程中，典型情况下雷诺数由低变高，与当前试验状态变化情况相反。因此，转捩过程中功率谱密度的变化规律应该与试验观测到的结果相反，即从层流到转捩再到湍流过程中，低频段能量优先发展起来，然后逐渐往高频扩展，这与边界层转捩过程中大尺度涡结构逐渐破碎直至发展成为湍流的过程相符。从图6—9 中也可以看出，转捩过程中，归一化的功率谱密度较湍流状态更高，并且低频段能量分布更多。这更容易激励器再入飞行器的结构响应，脉动压力预示时需要对该过程进行单独处理，环境工程及结构设计工程师在开展再入环境考虑以及结构设计时应该对此予以特别关注。

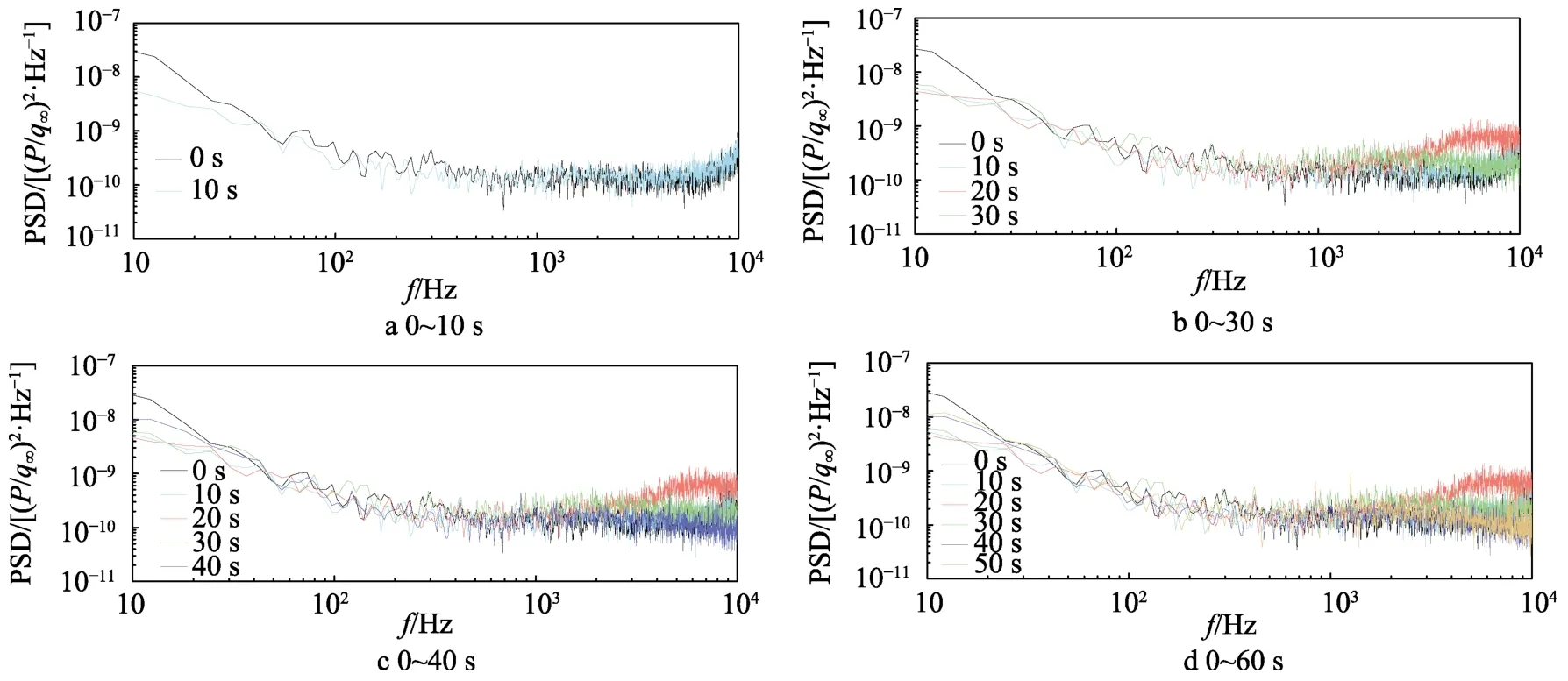
图7 x/L=0.64 处不同时刻归一化脉动压力功率谱密度Fig.7 The normalized surface pressure fluctuation PSD at x/L=0.64 of different time

图8 x/L=0.74 处不同时刻归一化脉动压力功率谱密度Fig.8 The normalized surface pressure fluctuation PSD at x/L=0.74 of different time

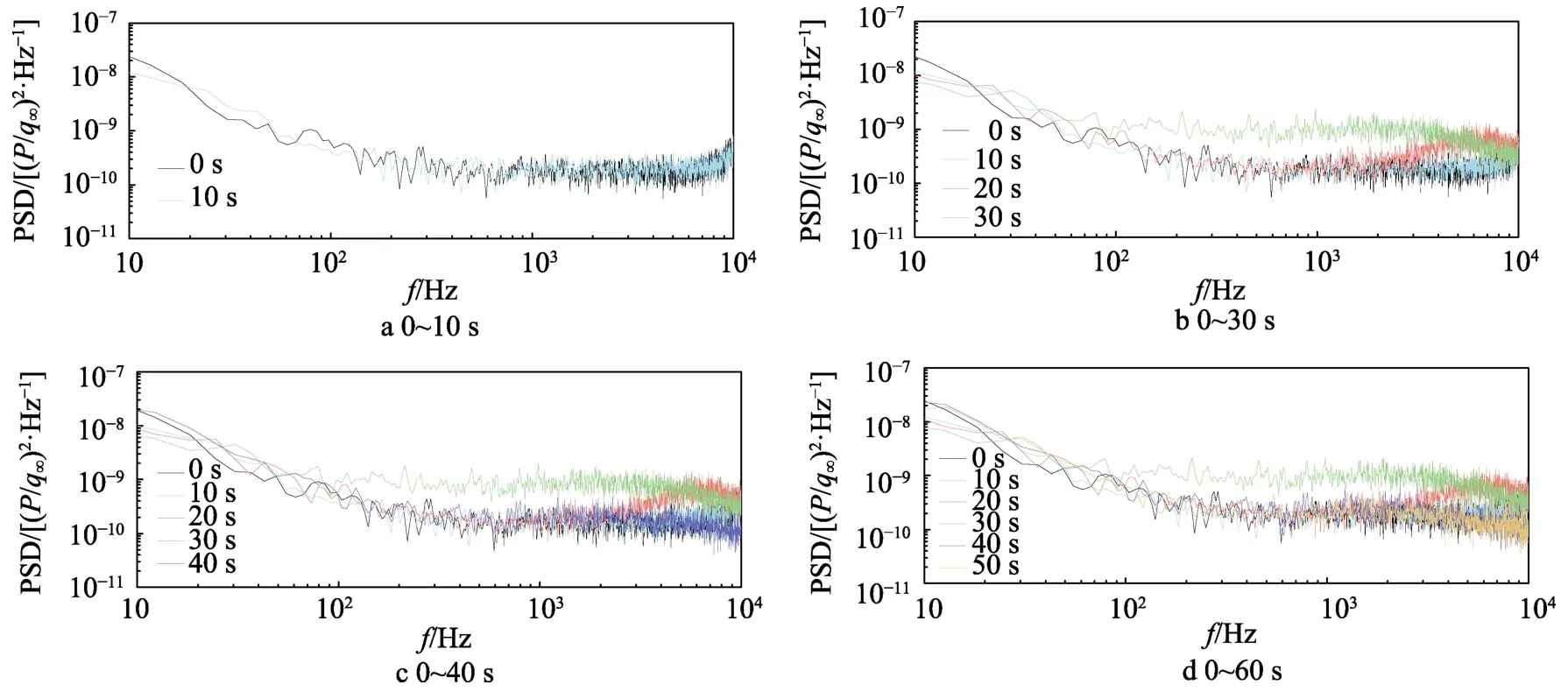
图9 x/L=0.84 处不同时刻归一化脉动压力功率谱密度Fig.9 The normalized surface pressure fluctuation PSD at x/L=0.84 of different times

4 结论

1）试验中观察到脉动压力时域及频率特征随边界层从湍流到转捩再到层流转变的变化。

2）在马赫数一定且边界层为湍流状态时，归一化的脉动压力频域特性基本与雷诺数无关。

3）边界层转捩时，脉动压力低频段能量较多，且归一化功率谱密度高于湍流状态，利用自由来流动压归一化的脉动压力均方根系数转捩状态约为湍流状态的2 倍。

4）由于转捩过程中脉动压力能量低频部分占比较多，转捩过程脉动压力预示需要进行单独考虑。