GLOBAL WELL-POSEDNESS FOR FRACTIONAL NAVIER-STOKES EQUATIONS IN VARIABLE EXPONENT FOURIER-BESOV-MORREY SPACES∗

Muhammad Zainul ABIDIN Jiecheng CHEN(陈杰诚)

College of Mathematics and Computer Science,Zhejiang Normal University,Jinhua 321004,China E-mail:zainbs359@gmail.com;jcchen@zjnu.edu.cn

Abstract In this paper we study the Cauchy problem of the incompressible fractional Navier-StokesequationsincriticalvariableexponentFourier-Besov-MorreyspaceWe prove global well-posedness result with small initial data belonging toThe result of this paper extends somerecent work.

Key words fractional Navier-Stokes equations;global well-posedness;Fourier-Besov-Morrey space

1 Introduction

We are concerned with the incompressible fractional Navier-Stokes(FNS)equations,

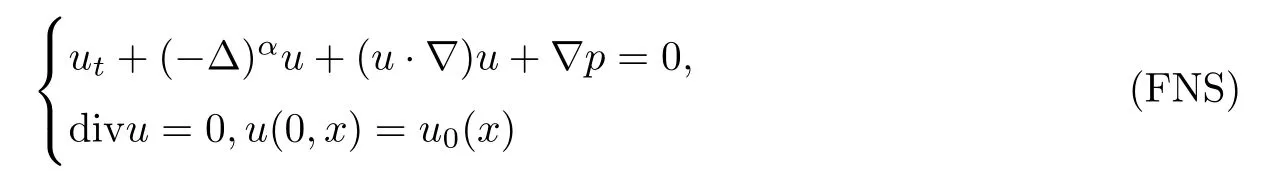
Recently,FNS equations have gained more attention as models were proposed to simulate fluid flows.The face-centred hypercubic(FCHC)lattice[1]for 3D has been shown to satisfy the incompressible Navier-Stokes equations.

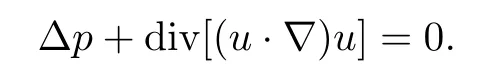
Let(u,p)be a smooth solution of the(FNS)equations.Taking the divergence of equation(FNS)and noticing that divu=0,we immediately obtain It follows that ∇p=(−∆)∇div[(u·∇)u].Introducing the Leray projector over divergence-free vector fields,namely P:=I+(−∆)∇div,equation (FNS) will be in the form

It is easy to see that the entries of P(u·∇)u are first order homogeneous Fourier multipliers applied to bilinear expressions.

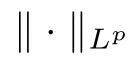
2 Preliminaries

Let Pbe the set of all measurable functions p(·):R→(0,∞]such that

For p ∈P(R) let L(R) be the set of all measurable functions f on Rsuch that for some λ>0,

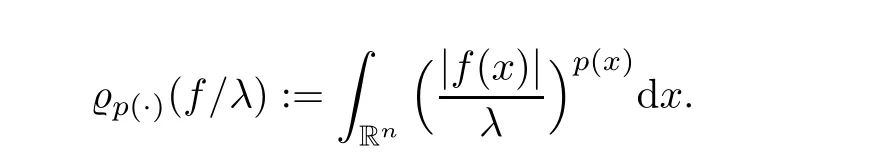
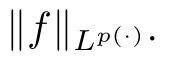
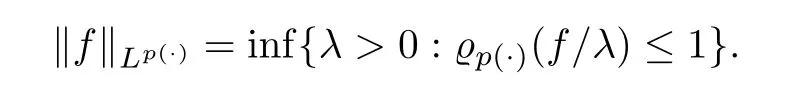
We postulate the following standard conditions to ensure that the Hardy-Maximal operator M is bounded on L(R):

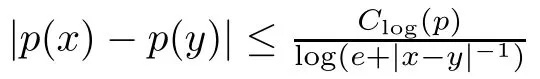
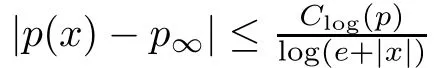
We use C(R) as the set of all real valued functions p:R→R satisfying 1) and 2).

The second norm on the right hand side is bounded by 1 due to the choice of δ.To show that the first norm is also bounded,we investigate the corresponding modular:

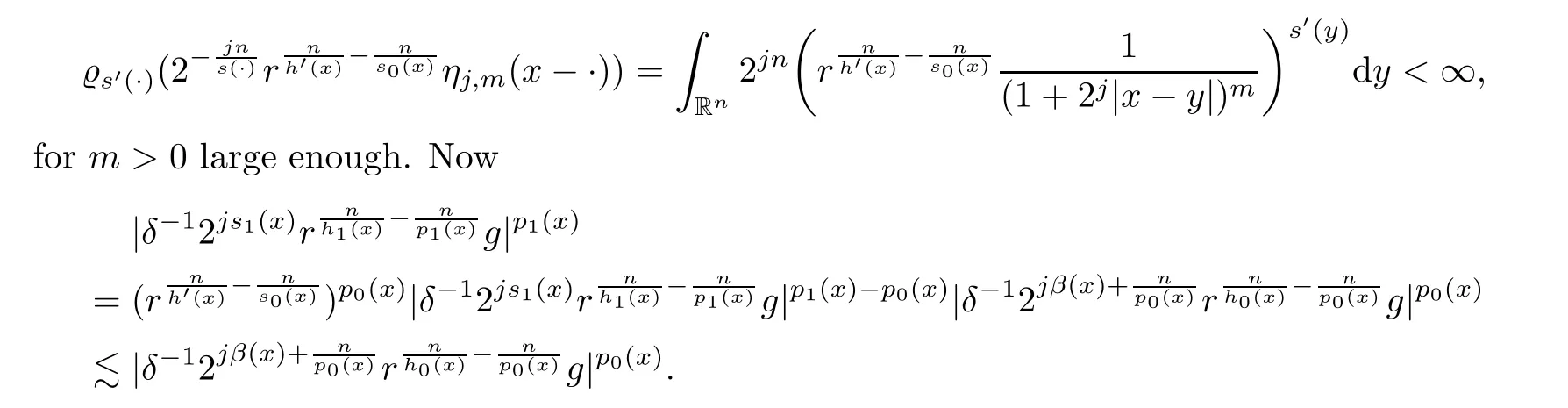
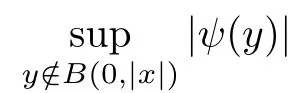
3 Well-posedness

In this section,from using the structure and propositions of the variable exponent homogeneous Fourier-Besov Morrey space,we study the global well-posedness of fractional Navier-Stokes equations in the frequency space with variable.It is clear that the solution u(x,t)of the Cauchy problem (FNS) is given by

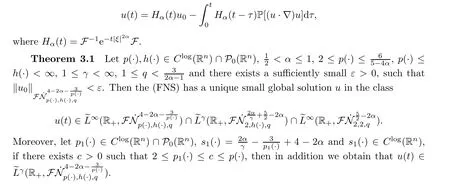
In a similar way to the case of space Y,it can be obtained that for

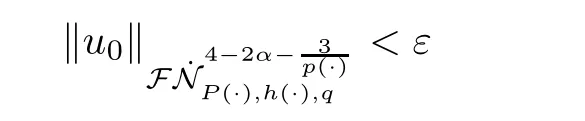
Acknowledgements

The authors would like to thank Dr.Ru Shaolei for useful discussions and helpful suggestions on this article.