ISOMORPHISMS OF VARIABLE HARDY SPACES ASSOCIATED WITH SCHRÖDINGER OPERATORS∗
Junqiang ZHANG(张俊强)
School of Science,China University of Mining and Technology-Beijing,Beijing 100083,China E-mail:jqzhang@cumtb.edu.cn
Dachun YANG(杨大春)†
Laboratory of Mathematics and Complex Systems(Ministry of Education of China),School of Mathematical Sciences,Beijing Normal University,Beijing 100875,China E-mail:dcyang@bnu.edu.cn
Abstract Let L:=−∆+V be the Schrödinger operator on Rn with n≥3,where V is a non-negative potential satisfying∆−1(V)∈L∞(Rn).Let w be an L-harmonic function,determined by V,satisfying that there exists a positive constant δ such that,for any x∈Rn,0<δ≤w(x)≤1.Assume that p(·):Rn→(0,1]is a variable exponent satisfying the globally log-Hölder continuous condition.In this article,the authors show that the mappings∋fwf∈Hp(·)(Rn)and(Rn)∋f(−∆)1/2L−1/2(f)∈Hp(·)(Rn)are isomorphisms between the variable Hardy spaces(Rn),associated with L,and thevariable Hardy spaces Hp(·)(Rn).
Key words variable Hardy space;Schrödinger operator;L-harmonic function;isomorphism;atom
1 Introduction
The theory of classical real Hardy spaces H(R)was first introduced by Stein and Weiss[25]in the early 1960s,and was then systematically developed by Fe ff erman and Stein[10].As a generalization of classical Hardy spaces,Nakai and Sawano[19]introduced variable Hardy spaces H(R)(see Definition 1.1 below),established their atomic characterizations,and investigated their dual spaces,where p(·):R→(0,1]is a measurable function.Independently,Cruz-Uribe and Wang[5]also studied the variable Hardy spaces H(R)with p(·)satisfying some conditions slightly weaker than those used in[19].Recall that it is well known that,if p(·)≡p∈(0,1]is a constant,then H(R)is just the classical Hardy space H(R).
Let P(R) be the set of all measurable functions p(·):R→(0,∞) satisfying

Then a function p(·) ∈P(R) is called a variable exponent function on R.Recall that a measurable function g ∈P(R) is said to be globally log-Hölder continuous,and denoted by g ∈C(R),if there exist constants C,C∈(0,∞)and g∈R such that,for any x,y ∈R,
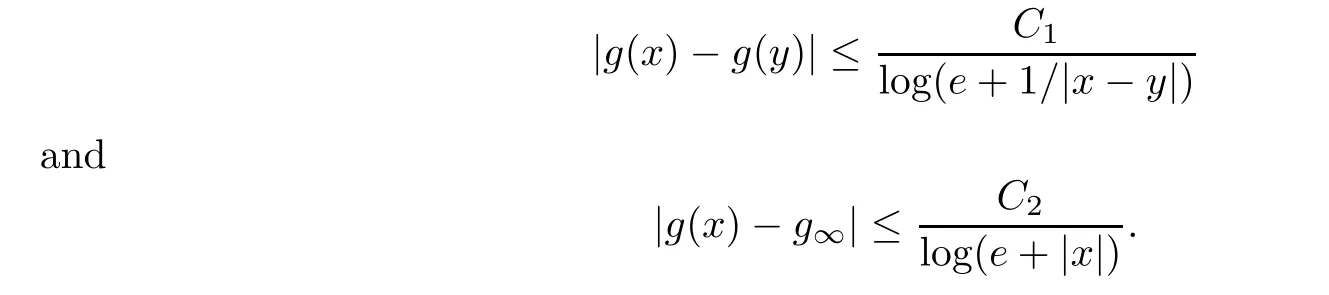
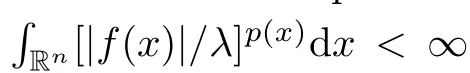

In particular,if p(·) ≡p ∈(0,∞) is a constant,then L(R) is just the classical Lebesgue space L(R).Let S(R) be the space of all Schwartz functions equipped with the well-known topology determined by a sequence of norms,and S(R) its dual space equipped with the weak-∗topology.The variable Hardy space H(R) is defined as follows:
Definition 1.1
([19]) Let p(·) ∈P(R).Then the variable Hardy space H(R) is defined by setting
By (1.3),we find that H(R) is essentially associated with the Laplacian operator ∆.Observe that the real-variable theory of function spaces and its applications are always active subjects of harmonic analysis(see,for instance,[2,11,13,17,18,24,27]),and,in recent years,there has been a lot of attention paid to the study of Hardy spaces associated with different operators (see,for instance,[7–9,12,14,22,23,26,28,31,34]).
In this article,we consider the Schrödinger operator
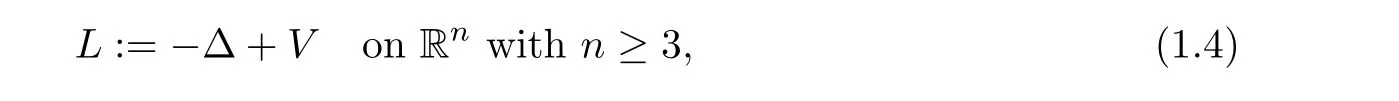
where ∆is the Laplacian operator on R,and V is a non-negative locally integral potential.Let{e}be the semigroup generated by L.Then,by the Feynman-Kac formula,we know that the integral kernel K(·,·) of {e}satisfies that,for any t ∈(0,∞) and x,y ∈R,

Remark 1.2
Since L is a non-negative self-adjoint operator,by [20,Theorem 7.3],we know that L generates a bounded holomorphic semigroup {e}on Σ.Here and hereafter,for any ν ∈(0,π/2],we always let
Moreover,for any given ν ∈(0,π/2),there exist positive constants Cand csuch that,for any z ∈Σand x,y ∈R,


where c:=Γ(n/2)/[2π(n −2)],and L(R) denotes the space of all essentially bounded measurable functions on R.
Now,we recall the notion of L-harmonic functions (see,for instance,[8,9,33]).
Definition 1.3
Let L be as in (1.4).A measurable function w on Ris said to be L-harmonic if w ∈D(L) (the domain of L) and L(w)=0.Remark 1.4
(i) By [8,Lemma 2.1],we know that a non-negative locally integrable potential V satisfies (1.7) if and only if there exist an L-harmonic function w and a positive constant δ such that,for any x ∈R,0<δ ≤w(x)≤1.Moreover,w is unique up to a positive constant multiple.In this sense,w is said to be determined by V.

Motivated by the results of [8,9,33],the main purpose of this article is to show that the mappings

The following two theorems are the main results of this article:






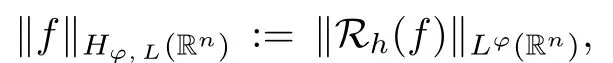




(v) In particular,for any x ∈Rand t ∈[0,∞),if ϕ(x,t) :=twith p ∈(0,1]in [33],then the conclusions of [33,Theorems 1.4 and 1.7]coincide with those of Theorems 1.6 and 1.7 when p(·) ≡p ∈(0,1]therein.In particular,if p(·) ≡1,then Theorems 1.6 and 1.7 coincide with [8,Theorem 1.1]and [9,Theorem 1.10],respectively.



2 Preliminaries

Remark 2.1
Let p(·)∈P(R).Then,
where the supremum is taken over all balls B of Rcontaining x.It is well known that,if p(·)∈C(R) and 1 We also have the following Fefferman-Stein vector-valued inequality of M on L(R),which was proved in [4,Corollary 2.1]: Lemma 2.2 Let q ∈[1,∞).Recall that a non-negative and locally integrable function w on Ris said to belong to the class A(R) of Muckenhoupt weights,denoted by w ∈A(R),if,when q ∈(1,∞), The following lemma is called the extrapolation theorem for L(R) (see,for instance,[4,Theorem 1.3]and [6,Theorem 7.2.1]): where U(B(x,t)) is as in (1.10) with B therein replaced by B(x,t),and where M is as in(2.1),and the implicit positive constants are independent of f and x. We now introduce the variable Hardy spaces associated with Rand S,respectively,as follows: Definition 2.6 In what follows,for any p(·)∈P(R) with 0 Now,we show that the above variable Hardy spaces coincide with each other. In this section,we give the proof of Theorem 1.6.To this end,we first recall the following lemma,which is just[30,Lemma 2.4],and which was essentially established in[21,Lemma 4.1]: where the implicit positive equivalence constants are independent of f,{λ},and {B},and A({λ},{B}) is as in (2.6).For any (p(·),2,M)-atom a associated with ball B,we claim that aw is a (p(·),2,0)-atom as in Definition 2.9.Indeed,by Definition 2.6,we know that there exists some b ∈D(L) such that a=L(b).From this,the fact that L is a self-adjoint operator,and w is L-harmonic,we deduce that By Lemma 2.10 and its proof,we know that H(R)∩L(R)is dense in H(R).Thus,we only need to show that,for any f ∈H(R)∩L(R),(3.5) holds true.Let f ∈H(R)∩L(R).Then,by Lemma 2.10(ii) and its proof,we find that there exist {λ}⊂C and a sequence {a}of (p(·),∞,s)-atoms with some s ∈Zsuch that By (2.5),we know that Ris bounded on L(R),where Ris as in (2.4).By this,(3.6),and(3.2),it is easy to see that,for almost every x ∈R, where U(B) is as in (1.10).From this and the fact that p∈(0,1],and from (i) and (ii) of Remark 2.1,we further deduce that Next,we show (3.8).By (2.5) and the fact that the Hardy-Littlewood maximal function M is bounded on L(R),we know that Ris bounded on L(R).From this and (3.2),it follows that,for any k ∈{0,···,10}, For any k ∈N ∩[11,∞),we consider the following two cases: Case 1 In this section,we prove Theorem 1.7.We begin by introducing the following basic estimates which were established in [9,p.924]: Lemma 4.1 (iii) Let 0 <η <δ <2.Then there exists a positive constant C :=Csuch that,for any x ∈Rand r ∈(0,∞), The following lemma is just [9,Lemma 4.5]: Lemma 4.2 The following lemma was established in [9,Lemmas 2.11 and 2.13]: Lemma 4.3 It is easy to see that supp M⊂2B,supp P⊂2B,and the above summation converges in L(R).By the Hölder inequality,we know that,for any given q ∈(1,∞) and any k ∈Z, Lemma 4.5 Proof To estimate I,for any µ ∈(0,π/2) and ζ ∈Σ,let F(ζ) :=ζ(1 −e),where Σis as in (1.6).It is easy to see that F is holomorphic and that there exists a positive constant where we used the fact that R(ζz)<0 and where A ∈(n −1,2M +n −1) is a constant fixed later.From this and (4.11),it follows that,for any x ∈Rand y ∈B, If x ∈2B,by the fact that q ∈(n,∞),we know that there exists some δ ∈(0,1)such that q >n/δ.Fix A:=n −δ as in (4.13).Then,by this,the Hölder inequality,and the fact that a is a (p(·),q,M)-atom,we find that,for any x ∈2B, If x ∈(2B),we fix A:=n as in (4.13).In this case,it is easy to see that,for any y ∈B,|x −y|∼|x −x|>2r.By this,(4.13),and the Hölder inequality,we further conclude that,for any x ∈(2B), We now show Theorem 1.7. Proof of Theorem 1.7 Indeed,since V satisfies (1.7),by Remark 1.4(i),we know that there exist an L-harmonic function w and a positive constant δ such that,for any x ∈R,0<δ ≤w(x)≤1.By Lemma 4.3,we know that To this end,we only need to show that,for any f ∈[H(R)∩L(R)],the above inequality holds true.Indeed,by Lemma 2.10(ii) and its proof,we know that H(R) ∩L(R) is dense in H(R)(see also[5,Section 4]),and,for any f ∈[H(R)∩L(R)],there exist a sequence{λ}⊂C and a family{a}of(p(·),∞,0)-atoms associated with balls{B}of Rsuch that This,together with the fact that L(−∆)is bounded on L(R) (see [9,Lemma 2.6]),implies that Let a be a (p(·),∞,0)-atom associated with a ball B of R,and w an L-harmonic function,determined by V,as in (4.20).We claim that where the implicit positive constant is independent of a and j.If this claim holds true,then,by Proposition 4.4,we conclude that where {a}is a family of (p(·),q,0)-atoms associated with balls {2B}.From this and (4.36),we deduce that Acknowledgements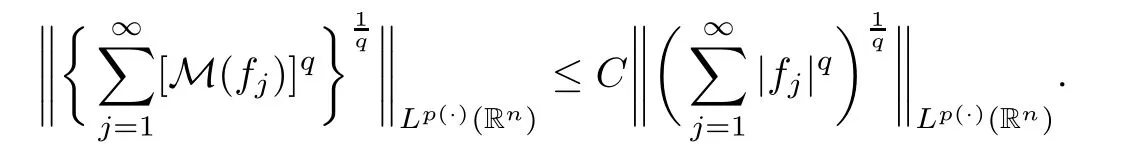





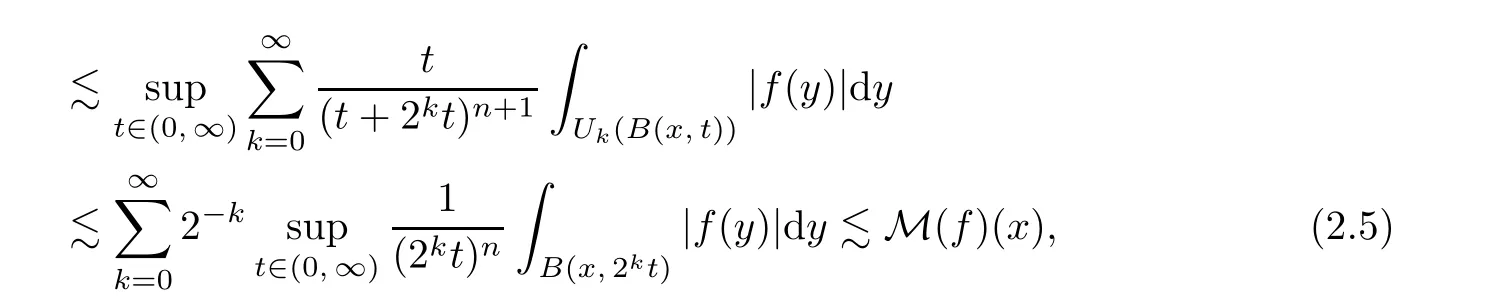


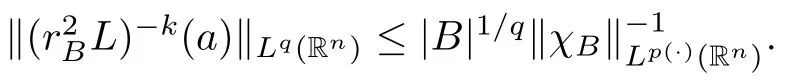




3 Proof of Theorem 1.6








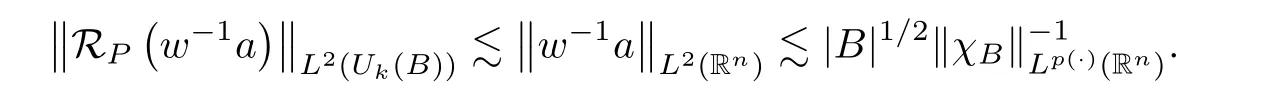


4 Proof of Theorem 1.7
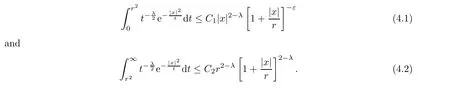
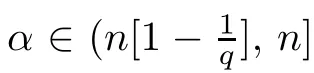

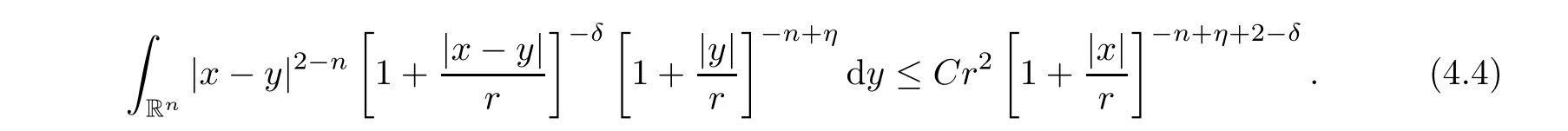
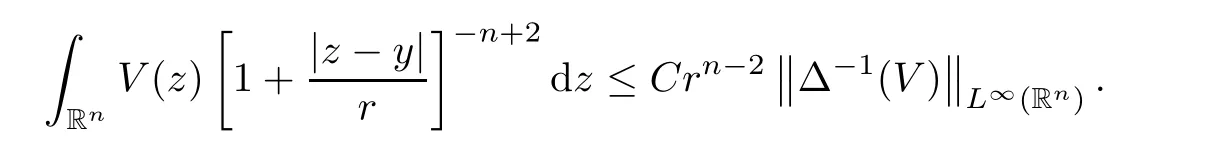















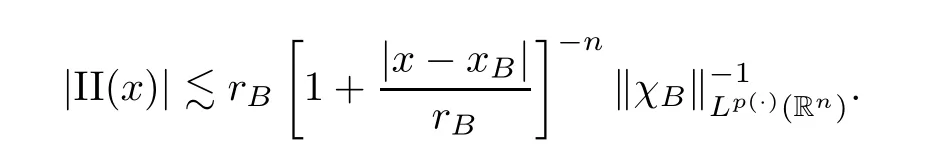













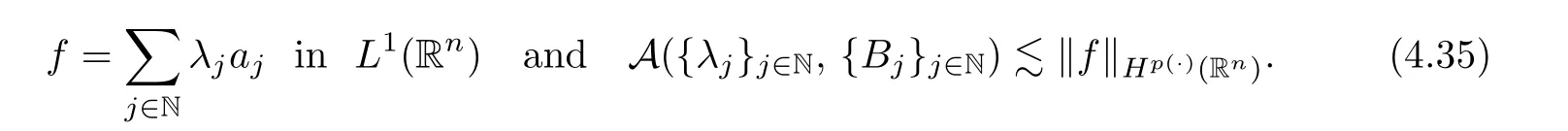

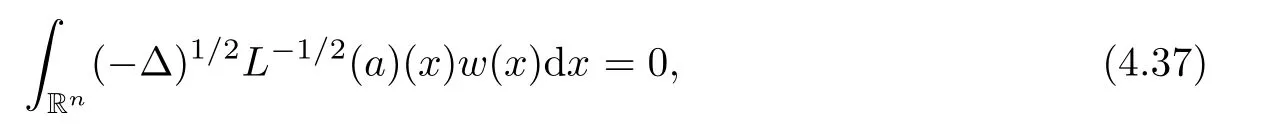







 Acta Mathematica Scientia(English Series)2021年1期
Acta Mathematica Scientia(English Series)2021年1期
