WEAK SOLUTION TO THE INCOMPRESSIBLE VISCOUS FLUID AND A THERMOELASTIC PLATE INTERACTION PROBLEM IN 3D∗
Srđan TRIFUNOVIĆ
School of Mathematical Sciences,Shanghai Jiao Tong University,Shanghai 200240,China E-mail:sergej1922@gmail.com;tarathis@sjtu.edu.cn
Yaguang WANG(王亚光)
School of Mathematical Sciences,MOE-LSC and SHL-MAC,Shanghai Jiao Tong University,Shanghai 200240,China E-mail:ygwang@sjtu.edu.cn
Abstract In this paper we deal with a nonlinear interaction problem between an incompressible viscous fluid and a nonlinear thermoelastic plate.The nonlinearity in the plate equation corresponds to nonlinear elastic force in various physically relevant semilinear and quasilinear plate models.We prove the existence of a weak solution for this problem by constructing a hybrid approximation scheme that,via operator splitting,decouples the system into two sub-problems,one piece-wise stationary for the fluid and one time-continuous and in afinite basis for the structure.To prove the convergence of the approximate quasilinear elastic force,we develop a compensated compactness method that relies on the maximal monotonicity property of this nonlinear function.
Key words fluid-structure interaction;incompressible viscous fluid;nonlinear thermoelastic plate;three space variables;weak solution
1 Introduction
Many models in applied fields such as aeroelesticity and hemodynamics can mathematically be described by the fluid-structure interaction(FSI)problems.Thus,there is a high need and motivation for their study in order to deepen our understanding,knowledge and develop the necessary mathematical tools.The main difficulties for such models arise due to the coupling of two systems,the geometric nonlinearity of the coupling itself and the fact that the domain of the fluid is not know a priori(a free boundary problem).
In recent years,the literature concerning the well-posedness of the FSI problems expanded drastically.In the context of the weak solutions,where displacement of the structure is described by a linear model,we mention the following results.The first such result was due to Chambolle et al.[3]which considered a viscoelastic linear plate interacting with viscous incompressible fluid.This result was then extended to purely elastic case by Grandmont ([11]).Muha and Čanić constructed an operator splitting+time discretization approximation scheme for this problem which they used to obtain various existence results in [23–27].Finally,we mention[18]where a linear shell model was considered with a different geometry-the shell is a closed regular 2D manifold that deforms in the normal direction.The compressible counterpart was considered in [2].In the context of strong solution where viscous incompressible fluid is interacting with a viscoelastic structure,first result was due to Beirão da Veiga[1]where a local solution was obtained for small initial data.Then,Lequerre obtained a local and global for small initial data solution in 2D case in[15]and extended this result to 3D case in[16].Grandmont et al.proved the existence of a unique global solution for 2D model in [12]by proving that no collision occurs between the 1D viscoelastic structure and the bottom of the cavity.In[13],a local strong solution in 2D was obtained that includes the cases when the 1D structure is purely elastic (rod and beam in flexion equations) that is of hyperbolic nature,contrary to the previous results for strong solutions where the structure is parabolic.Finally,we mention a recent result[19]for model where 2D compressible fluid interacts with 1D viscoelastic structure,for which a highly regular local solution was obtained.

Here,we aim to extend our result[29]by including the temperature in the plate which obeys the heat law,so the plate is modeled by a system of two equations.The approximate scheme we construct here quite successfully deals with this additional equation.This is mainly because the heat equation is only coupled with the plate equation,but not with the momentum equation of the fluid.We also include a special quasilinear case which was studied in [14,17]where the nonlinearity in the plate equation takes the form ∆(∆w)with w being the lateral displacement of the plate.To pass to the limit from the approximate solutions to the weak solution of the original problem,one faces a difficulty in proving that this approximate nonlinear function converges to the right limit,since we do not have any information on derivatives of ∆w.To overcome this difficulty,we implement the compensated compactness method,which relies on the maximal monotonicity property of this nonlinear function and on proving a certain inversetype inequality by comparing the approximate and limiting nonlinear function.This is not a straightforward task because the approximate problem is of hybrid nature while the original problem is just time-continuous,because the momentum and plate equation are coupled into one equation in the weak form and because the approximate solutions and the limiting solution are not defined on the same physical domain.Due to these reasons,the proof is technical,but the underlying idea remains simple.
This paper is organized as follows.In Section 2 we introduce the problem,its weak formulation and the main result.Then,in Section 3,we use the operator splitting method and a hybrid discretization in time to construct the approximate problems including the structure sub-problem and the fluid sub-problem,and study the a priori estimates and convergence of the approximate solutions.Finally,in Section 4,we obtain the convergence of the approximate nonlinear term in the plate equation and conclude the main result.
2 Preliminaries and Main Result
In this section,we will introduce the problem we will deal with.Then,we will give its weak formulation and state the main result.
2.1 Model description
Here,the incompressible viscous fluid is interacting with a thermoelastic nonlinear plate.The displacement of the plate is described by a scalar function w :(0,T)×Γ →R,where Γ ⊂Ris a connected and bounded Lipschitz domain.The plate also possesses a temperature which is described by θ :(0,T)×Γ →R.The fluid fills the time dependent domain
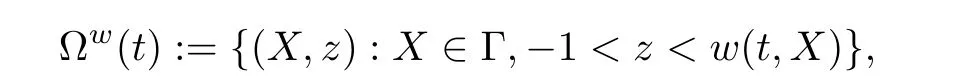
where the boundary ∂Ω(t) consists of the rigid part Σ :=Γ×{−1}∪∂Γ×(−1,0) and the elastic part Γ(t):=((X,w(t,X)):X ∈Γ).The fluid velocity is described by a vector function u:(0,T)×Ω(t)→R.The problem we will study is the following:
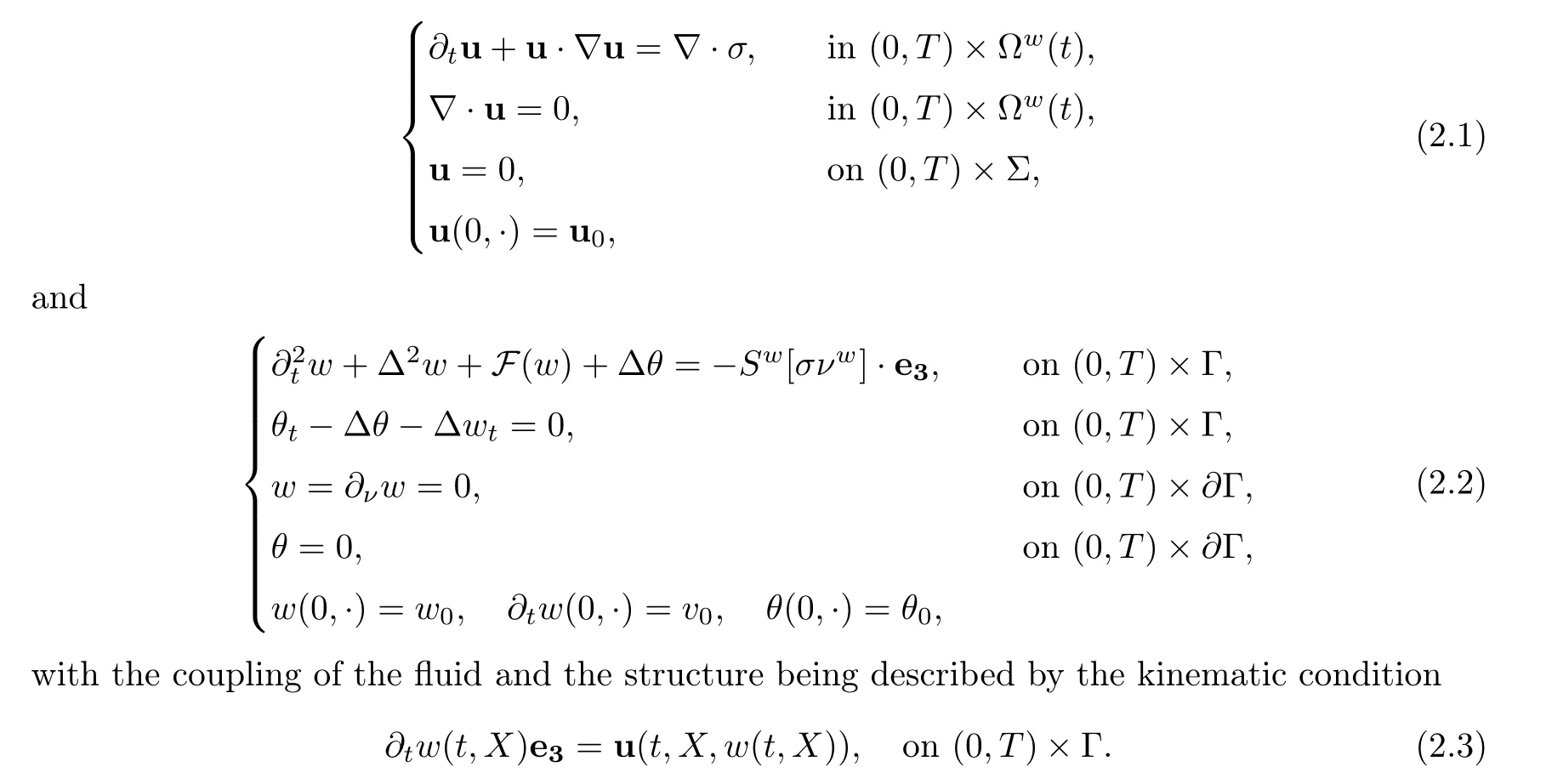

The nonlinear elastic force F corresponds to one of the two following cases:

2.2 Formulation of the weak solution
Here we want to transform the fluid system(2.1)to be defined on the fixed reference domain

For this reason,for a fixed w(t,X),we define a family of mappings (so called arbitrary Lagrangian-Eulerian(ALE) transformations):


1.The pullback by A:f(t,X,z):=f(t,A(t,X,z)),for (X,z)∈Ω ;
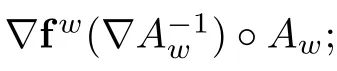
3.The transformed divergence of f:∇·f :=Tr(∇f).

1.Lower regularity of the transformed velocity.The transformation Ais not necessarily Lipschitz,so the transformed velocity umay not be in L(0,T;H(Ω)),but rather in L(0,T;W(Ω)) for any p<2;


Definition 2.1
(functional spaces) We define the space for the fluid velocity on the fixed reference domain Ω


Now,we introduce the concept of the weak solution:



Remark 2.4
(1) The Case A plate model.A similar semilinear plate model was studied by Chueshov in [4,5]where the plate interacts with linearized viscous compressible fluid and with linearized inviscid incompressible fluid,respectively,and by the authors in [29]where the existence of a weak solution was obtained for the nonlinear fluid-structure interaction system.In these works,one does not concern the effect of temperature change.Such semilinear plate model is a generalization of the Kirchhoff,von Kármán and Berger plate models for which there is a vast literature dedicated to their study (see for example [6–8]and the references therein).Additionally,we mention [28],where the interaction of thermoelastic von Kármán plate with linearized potential subsonic gas flow was considered.
3 Approximate Problems
In this section we introduce the approximate problems for solving the weak solution of(2.1)–(2.3) defined in Definition 2.2.Then,we will solve these approximate problems and obtain the uniform estimates and the convergences of the approximate solutions.
3.1 Formulation of approximate problems
Let N ≥1 be given.We split the time interval [0,T]into N equal sub-intervals of length∆t=T/N and on each of the sub-intervals we split (decouple) the problem into two subproblems by using the Lie operator splitting.The resulting sub-problems are solved one at the time with the data from the previous steps (a time-marching scheme).We will define them in the following two sections.
Remark 3.1
(1) The sub-problems are of different nature,i.e.,the fluid sub-problem is stationary while the structure sub-problem is continuous in time and in a finite Galerkin basis.The main reason for developing such a hybrid approximation scheme was the general form of nonlinearity F in the plate equation (2.2)which couldn’t be discretized in time in such a way that the energy of the approximate solutions is properly bounded,unlike the cases in [23–27]where one doesn’t face this difficulty and both sub-problems are stationary.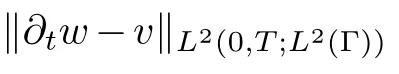
(3) When we sum up the fluid and the structure sub-problems(with common test function),the resulting system will eventually converge to the original system in the sense of Definition 2.2.
3.1.1 The structure sub-problem (SSP)




3.1.2 The fluid sub-problem (FSP)
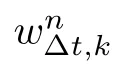

3.2 Solving the approximate problems

3.2.1 Uniform estimates and the solutions of (SSP) and (FSP)
Lemma 3.2
There exists a unique solution (θ,w) of (SSP) that satisfies the following energy identity:
Proof
First notice that in (SSP),due to the operator splitting,we only have first order time derivative of the plate displacement in both equations.We want the leading order term of wto be in the first equation of (SSP) in order to solve this system.Therefore,we add an artificial second order time derivative in the plate equation to obtain the following auxiliary system (SSP):
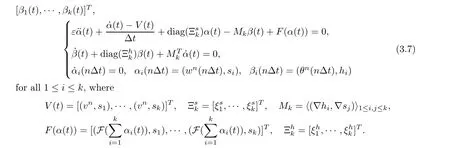
Set γ(t)=α(t).It is easy to know that the system given in (3.7) can be rewritten as the following first order system for the unknown (α(t),γ(t),β(t))
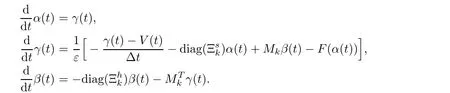
with the obvious choice for the initial data.To solve this problem,it is enough to prove that the function F is uniformly Lipschitz for a fixed ε.For the Case A,one can use the local Lipschitz continuity from the assumption (A1) where the Lipschitz constant is now uniform by the coercivity property of the potential Π given in (A2) and (3.6).For the Case B,we have



3.3 A priori estimates of the approximate solutions
The goal of this subsection is to derive a priori estimates for the approximate solutions defined as follows

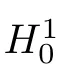

(iv) ∂w,vand uare bounded in L(0,T;L(Γ)),L(0,T;L(Γ))and L(0,T;L(Ω)),respectively,uniformly with respect to ∆t,k.

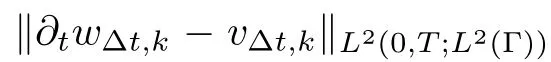


Lemma 3.5
Assuming that N(k)satisfies(3.11),for a constant C depending only on the initial energy and some given parameters in the system,the following estimates hold:
3.4 The convergence of the approximate solutions
Here we want to prove that the approximate solutions obtained in the section 3.2 converge(weakly or strongly) in appropriate functional spaces:




4 Proof of the Main Result
Here we aim to prove that the limiting functions (θ,u,w) obtained in Lemma 3.6 are weak solutions in the sense of Definition 2.2.First notice,since the heat equation (2.8) is linear in θ and w,we immediately obtain by Lemma 3.6 that θ and w satisfy this equation.The remainder of this section focuses on proving that (θ,w,u) satisfy (2.9).
For given test functions (q,ψ) ∈Q(0,T) (where w is the weak limit of wgiven in Lemma 3.6),we need to construct suitable approximate test functions that will converge alongside the approximate solutions (θ,w,u).This construction of the piece-wise stationary approximate test functions(q,ψ)and their strong convergence in appropriate functional spaces is rather tedious and can be done in the same way as in [29,Section 5.1],so we omit it here.
Now,we sum up(3.2)and(3.3)tested by ψand(q,ψ),respectively,to obtain:


where G is the weak limit of F(w).The energy estimates(2.10)and(2.11)follow from(3.9).The lifespan of the solution T given in Theorem 2.3 can be obtained by repeatedly prolonging the solution (see [3,pp.397-398]or [29]for more details).It remains to identify the limit G.This is done in the following section.
4.1 Identifying the limit G
Throughout this section we assume that N=N(k) satisfies the condition (3.11).This implies that when we let k →+∞,then ∆t(k)→0 as well.
4.1.1 Case A
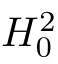

Notice that here the Lipschitz constant C is now uniform with respect to ∆t and k due to Lemma 3.4(iii).Now,by the compact embedding of C(0,T;H(Γ)) into C(0,T;H(Γ)),for 2α<ǫ,the right hand side of (4.3) converges to 0 as k →+∞so we obtain that G=F(w) in H(Γ),for all t ∈[0,T].
4.1.2 Case B
In this case,we cannot use the standard compactness arguments as above to pass the convergence in the nonlinear term F(w) since the order of nonlinearity is too high.To overcome this difficulty,we turn to the compensated compactness method instead:
Lemma 4.1
We have
Proof
Here we follow the ideas given in [17].Since F(w)=∆(∆w)is a maximal monotone operatorfrom W(Γ) into its dual,by [7,Proposition 1.2.6],it is enough to prove the following inverse type inequality







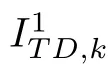
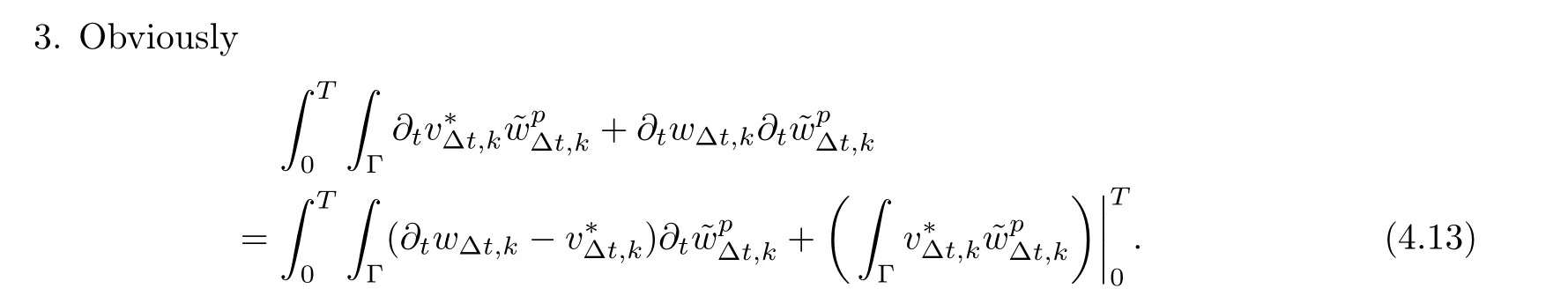

 Acta Mathematica Scientia(English Series)2021年1期
Acta Mathematica Scientia(English Series)2021年1期
- Acta Mathematica Scientia(English Series)的其它文章
- CONTINUOUS DEPENDENCE ON DATA UNDER THE LIPSCHITZ METRIC FOR THE ROTATION-CAMASSA-HOLM EQUATION∗
- ISOMORPHISMS OF VARIABLE HARDY SPACES ASSOCIATED WITH SCHRÖDINGER OPERATORS∗
- HITTING PROBABILITIES OF WEIGHTED POISSON PROCESSES WITH DIFFERENT INTENSITIES AND THEIR SUBORDINATIONS∗
- INHERITANCE OF DIVISIBILITY FORMS A LARGE SUBALGEBRA∗
- SOME SPECIAL SELF-SIMILAR SOLUTIONS FOR A MODEL OF INVISCID LIQUID-GAS TWO-PHASE FLOW∗
- THE AVERAGE ABUNDANCE FUNCTION WITH MUTATION OF THE MULTI-PLAYER SNOWDRIFT EVOLUTIONARY GAME MODEL∗
