ON THE CAUCHY PROBLEM FOR AW-RASCLE SYSTEM WITH LINEAR DAMPING∗
Juan C.JUAJIBIOY
Escuela de Matem´aticas y Estad´ıstica,Universidad Pedag´ogica y Tecnol´ogica de Colombia,Tunja 15001,Boyac´a,Colombia E-mail:juan.juajibioy@uptc.edu.co
Abstract The existence of global BV solutions for the Aw-Rascle system with linear damping is considered.In order to get approximate solutions we consider the system in Lagrangian coordinates,then by using the wave front tracking method coupling with and suitable splitting algorithm and the ideas of [1]we get a sequence of approximate solutions.Finally we show the convergence of this approximate sequence to the weak entropic solution.
Key words wave front tracking;global weak entropy solutions;linear damping
1 Introduction
Traffic flow is one of the many application of hyperbolic systems of conservation laws,in 1997 Aw and Rascle [2]introduced a new model of traffic flow in order to improve some drawbacks presents in the old model of Lighthill-Whithan,this model is given by the 2×2 system of conservation laws

where w=v+P(ρ) and the unknowns functions ρ=ρ(x,t) and v(x,t) represents the density and the velocity of cars on the road.In this paper we consider the following conditions on the pressure function
C1.The function p(ρ) is smooth and strictly increasing which satisfies the following conditions
C2.

For the justification of that condition the interested reader can see [2].
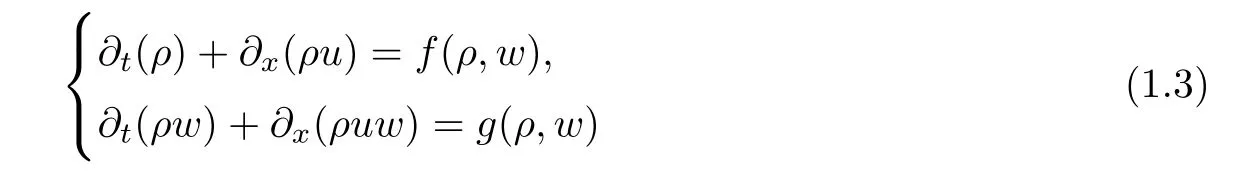

In [4]the existence of global weak entropy solution was considered in the Lsetting by using the vanishing viscosity and the compensated compactness methods.Motivated by these results,in this paper we consider the case in which the linear damping term appears,this is a theoretical motivation but we will show a specific implication of the source term in the behavior of the pressure.We consider the system

Notice that the first characteristic field is genuinely non linear and the second one is linear degenerate.Moreover the respective Riemann invariants are given by w=constant,v=f(τ)−w.
A physical motivation to consider the linear damping can be interpreted from (1.5),notice that the second equation w=−w implies that the solution w(X,T) converges exponentially to 0,since w=v+P(ρ) this relation implies that the densitity goes to zero,that holds by C1.
2 Riemann Problem
In order to introduce the wave front tracking algorithm,first we consider the Riemann problem for the homogeneous case of (1.5),
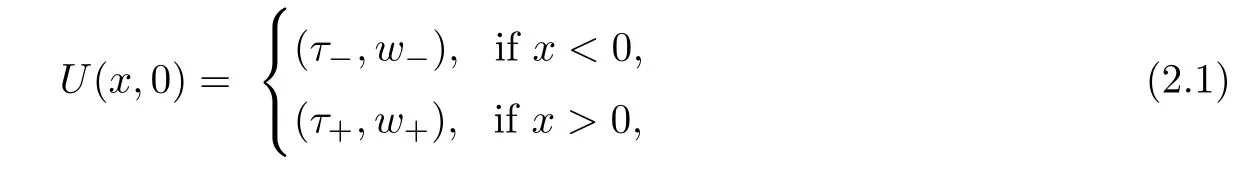
First at all notice that for w constant the system (1.5) reduces to the scalar conservation law
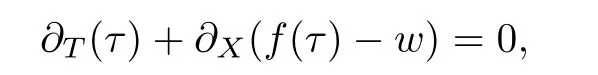
and in this case,by the condition (1.2) the flux function is convex,so the solution of the Riemann problem is given by a rarefaction if τ<τand by a shock if τ>τ.Now we construct the solution of the Riemann problem(1.5),(2.1).First we compute and intermediate state τby solving the equation w=f(τ)−w,by the above observation the solution of the Riemann problem is given as follows:given two states (τ,w),(τ,w) connected the state(τ,w) to the intermediate state (τ,w) by a 1-rarefaction or 1-shock.Then connect the state (τ,w) to the state (τ,w) by a 2-contact discontinuity.In the following figure the integral curves of the eigenvector and a a solution of the Riemann problem are presented.
In the Figure 1 the solution is given by a 1-rarefaction wave followed by a 2-contact discontinuity.
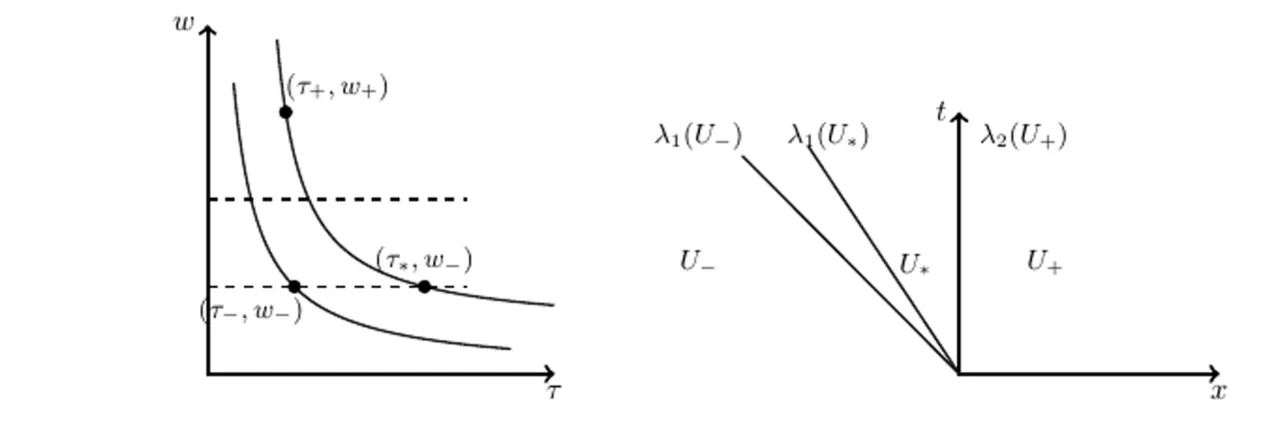
Figure 1 Characteristic curves
3 The Wave front Tracking Algorithm for 2×2 System
In this section we let us to describe the wave front tracking algorithm to get an approximate solution to the Cauchy problem
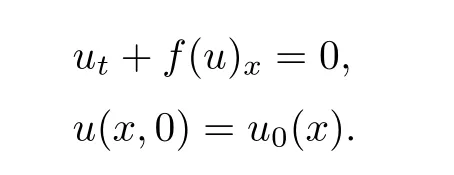
First we consider an piecewise constant approximate solution for the initial data u.If {x} is the set of discontinuity point of u we solve the Riemann problem with initial data
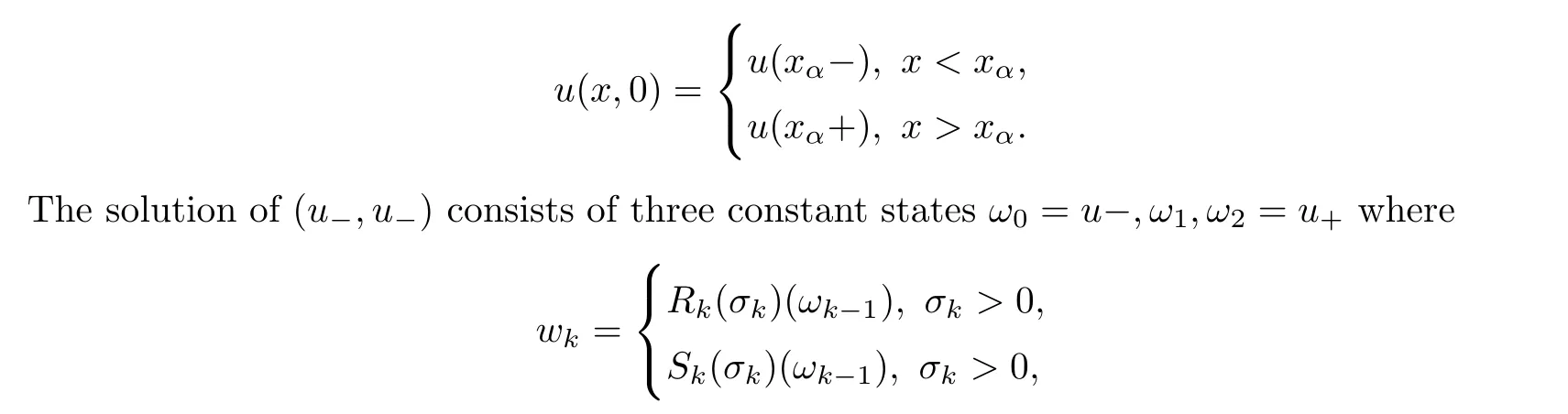
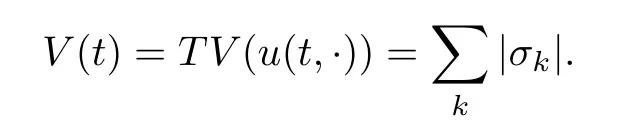
Time t where two waves collide time is called the interaction time.In this case a new Riemann problem arises.We solve the new Riemann problem and follow so on until a new interaction time occurs.Consider a time where two fronts of strength σ,σ,collide the holds
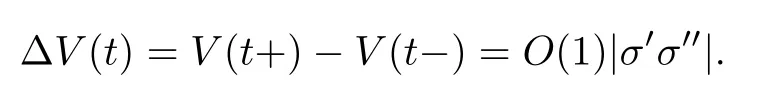
In the Figure 2 we show the collition of 1-shock with a 2-contact discontinuity.At xthe Riemann solution is given by a shock conecting the states u(x−)=ωwith u(x+)=ω,the intermediate states is ω,the strength of the first wave is σ=|ω−ω| and the speed is given by the speed of shock that we denote s(ω,ω) and strength σ=|ω−ω|.An interaction occurs at time tand a new Riemann problem arises,in this case the solution is given by a new shock,notice that the total variation for t>tis given by
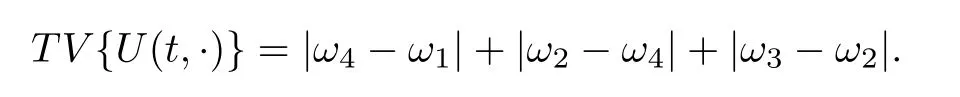
In essence the wave front tracking produces an approximate solution uby considering and piecewise constant approximation of the initial data.At time were two waves collide a new Riemann problem is solved and so on,is known that the set of interaction time is finite and the total variation of the approximate solution is decreasing at each time.
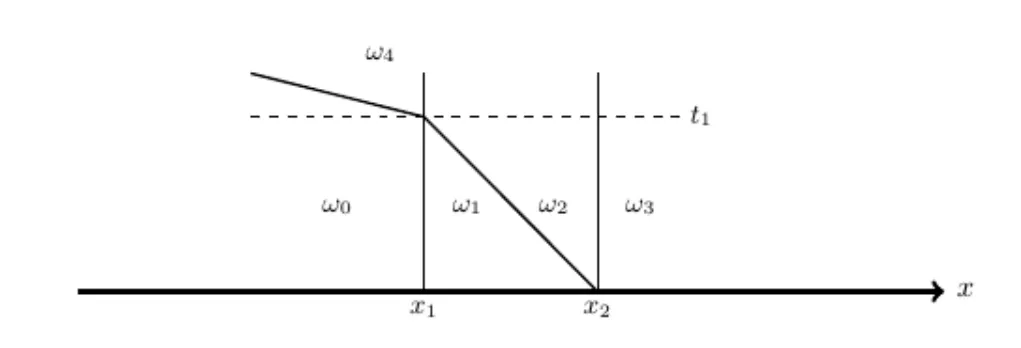
Figure 2 Collition of shocks
4 The Splitting Wave front Tracking Approximation and a Priori Bounds
Following [1,6],we construct the following approximation.Define the following sets
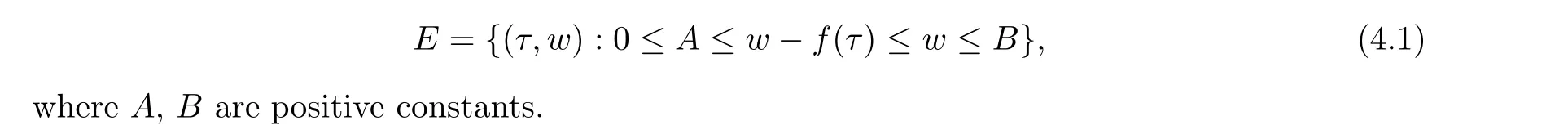
Moreover is known that the class of system consider here is of Temple class and by [7]the solution generates a Lcontractive,whose domain is
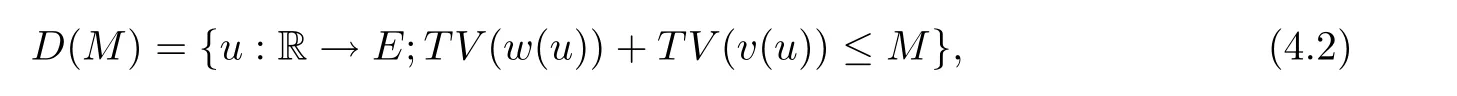
1.Consider the approximation of initial data.
2.For each ν ∈N solve the non homogeneous system
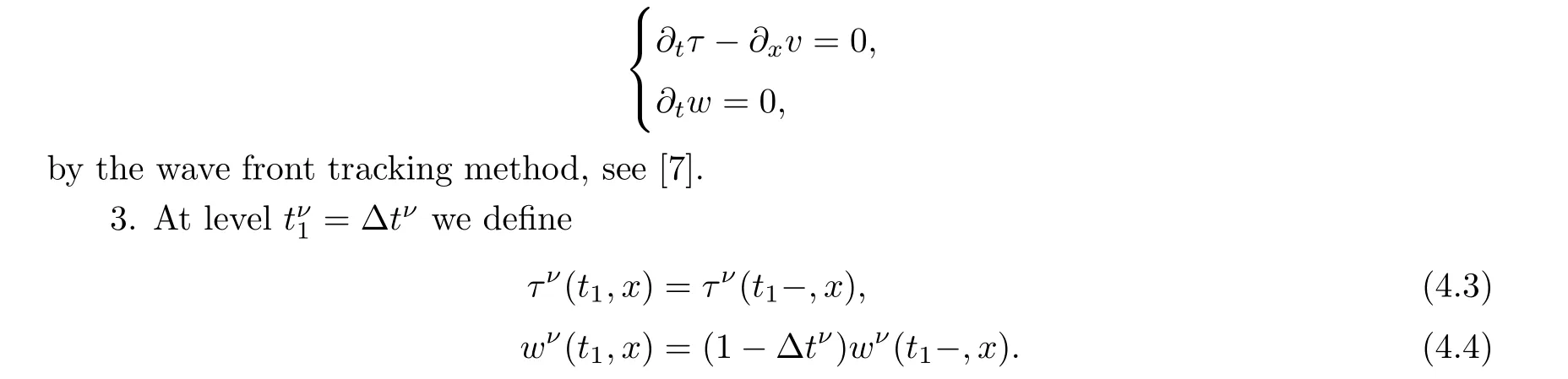
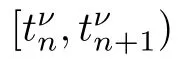
In order to achieve a priori bounds we need a positive invariant region,roughly speaking a positive invariant region is a bounded region M such that if the initial data belongs to M then for any time t>0 the solution still belongs to M see [8,9].

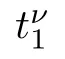


5 Convergence of the Approximate Solution
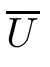
Theorem 5.1
Let us denote U=(τ,w) ∈D(M) for some fixed M >0.Denote by U=(τ,w) the limit of the approximate solution U=(τ,w) obtained by the splitting wave front tracking as ν →∞.Then U is a weak entropy solution of (1.5),(1.6)Proof
Making U=(τ,w),F(U)=(w −f(τ),0) and G(U)=(0,−w),system (1.5) can be written as a inhomogeneous system of conservation laws,
In order to define a weak solution take a finite time T >0,we let us denote Ω=[0,T)×R and take an arbitrary test function Φ=(φ,ψ).By definition [10]U is a weak solution of (1.5)if
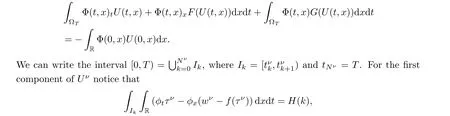

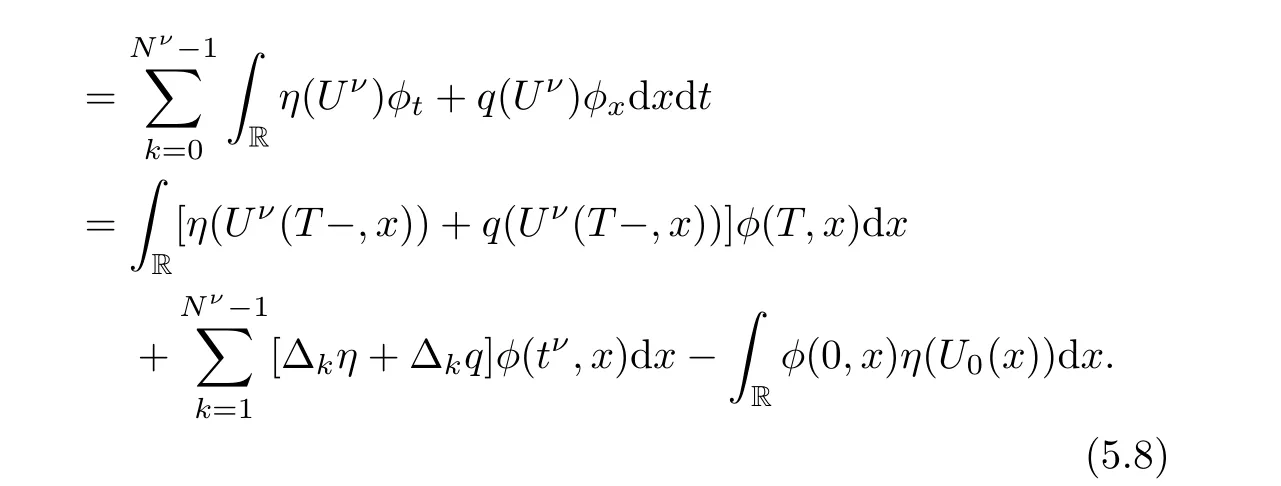
Notice that by the first condition on the entropy relation we have that ∆q=0.For ∆η we have
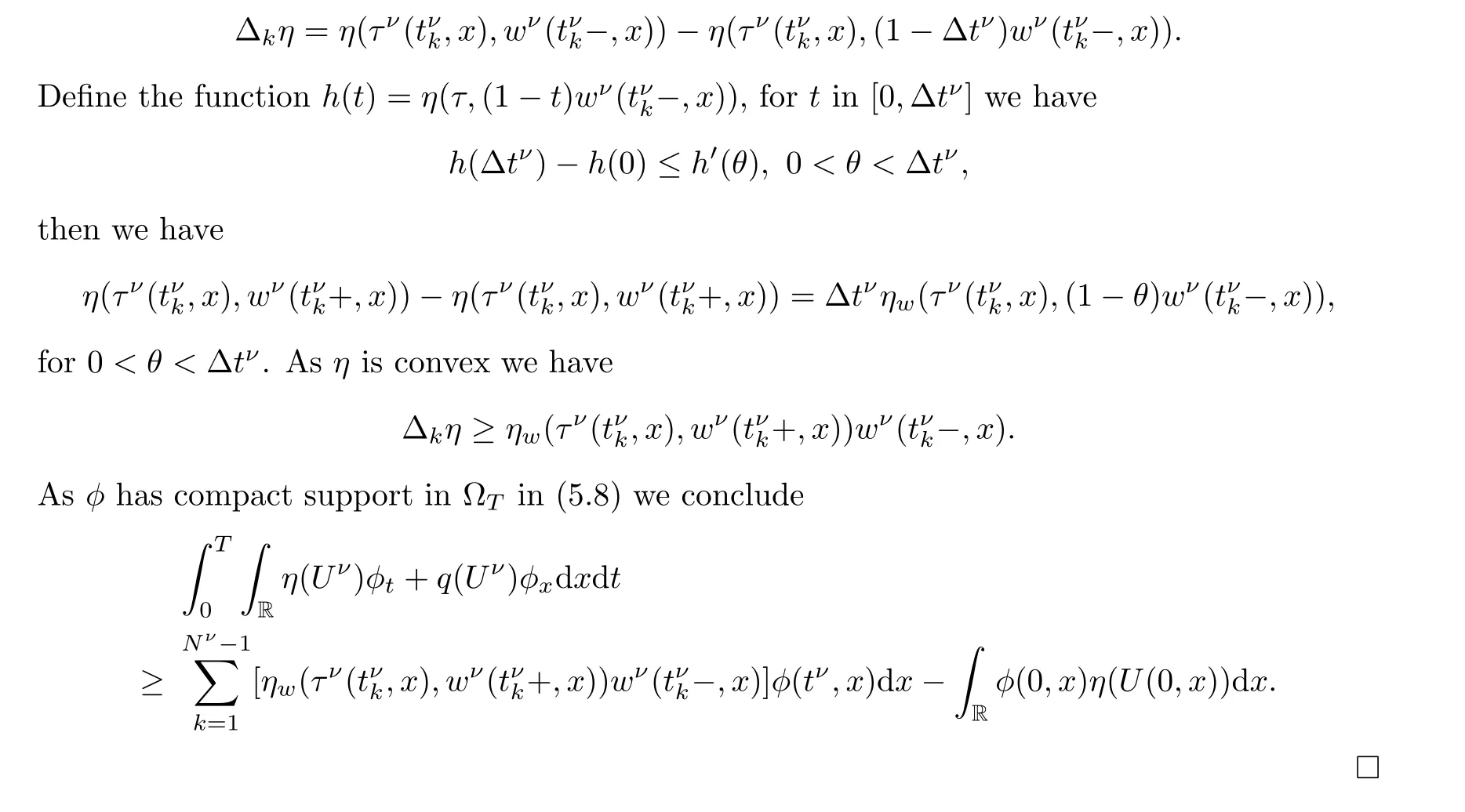
 Acta Mathematica Scientia(English Series)2021年1期
Acta Mathematica Scientia(English Series)2021年1期
- Acta Mathematica Scientia(English Series)的其它文章
- CONTINUOUS DEPENDENCE ON DATA UNDER THE LIPSCHITZ METRIC FOR THE ROTATION-CAMASSA-HOLM EQUATION∗
- WEAK SOLUTION TO THE INCOMPRESSIBLE VISCOUS FLUID AND A THERMOELASTIC PLATE INTERACTION PROBLEM IN 3D∗
- ISOMORPHISMS OF VARIABLE HARDY SPACES ASSOCIATED WITH SCHRÖDINGER OPERATORS∗
- HITTING PROBABILITIES OF WEIGHTED POISSON PROCESSES WITH DIFFERENT INTENSITIES AND THEIR SUBORDINATIONS∗
- INHERITANCE OF DIVISIBILITY FORMS A LARGE SUBALGEBRA∗
- SOME SPECIAL SELF-SIMILAR SOLUTIONS FOR A MODEL OF INVISCID LIQUID-GAS TWO-PHASE FLOW∗
