基于深度学习的重力异常与重力梯度异常联合反演
张志厚, 廖晓龙, 曹云勇, 侯振隆, 范祥泰, 徐正宣,,路润琪, 冯涛, 姚禹, 石泽玉
1 西南交通大学地球科学与环境工程学院, 成都 611756 2 西南交通大学高速铁路线路工程教育部重点实验室, 成都 610031 3 中铁二院成都地勘岩土工程有限责任公司, 成都 610000 4 东北大学深部金属矿山安全开采教育部重点实验室, 沈阳 110819 5 东北大学资源与土木工程学院, 沈阳 110819
0 引言
重力物性反演是典型的线性反问题,存在多解性,设计合理的反演算法是关键步骤之一.为获得稳定、准确的反演结果,一些正则化方法被引入到重力数据的线性反演中,并取得了较好的计算结果.如:基于地质异常体最小体积约束方法及其改进方法(Last and Kubik, 1983; Guillen and Menichetti, 1984; Barbosa and Silva, 1994; Li and Oldengburg, 1998; Silva and Barbosa, 2006; Dias et al., 2009, 2011)和基于最小梯度约束的“聚焦反演”(Portniaguine and Zhdanov, 1999; Zhdanov et al., 2004; Zhdanov, 2009)等.此外,为了抑制反演的“趋肤效应”(Fedi et al., 2005),将深度加权函数引入到目标函数中进行反演(Li and Oldengburg, 1998; Chasseriau and Chouteau, 2003; Commer, 2011)的方法在一定程度上提高了深度分辨率,以及加入其他地质先验信息或密度模型的重力反演方法(Shamsipour et al., 2010)也取得了较好的效果.随着FTG(Full Tensor Gravity Gradiometry)系统的问世与成功应用,以上诸多方法也被应用在重力梯度数据的反演中(Martinez et al., 2013; Geng et al., 2014; Lu and Qian, 2015; 高秀鹤等,2017).由于重力梯度数据能够提供更丰富的地质信息,因此利用重力及重力梯度数据联合反演不仅能够更加准确的勾画出地下异常体的物性大小与空间分布特征,而且联合反演也是约束多解性的一种重要手段(Gallardo and Meju, 2003; Fregoso and Gallardo, 2009; Zhdanov et al., 2012).于是重力及重力梯度数据的联合反演方法与技术研究备受诸多学者关注(Wu et al., 2013; Qin et al., 2016; 秦朋波和黄大年,2016).但线性类反演方法通常容易陷入局部极小,并且计算效率低、稳定性差(徐世浙等,2009).在实际应用中,只有选择良好的初始模型,线性类反演方法才可能获得较为可靠的结果,然而初始模型应包含有关地质体属性的先验信息,对于空间复杂的地质情况,通常很难对其进行可靠的估算.
大数据时代的到来,人工智能的兴起,聚类(Sun and Li, 2015;Liu and Jin, 2020)、决策树(戴诗华等, 2010;Barak et al,. 2020)、支持向量机(Li et al., 2020a)、贝叶斯(Guo et al., 2011; 殷长春等, 2014; Jiang et al., 2016)及人工神经网络(Artificial Neural Network, ANN)(Al-Garni, 2009, 2013, 2015; Neyamadpour et al., 2010)等机器学习方法被引入到地球物理数据的处理中.利用机器学习的方法进行反演无需依赖初始模型,也不需要对灵敏度矩阵进行计算和存储,并且有着良好的全局寻优性能,此类方法已逐步成为地球物理数据处理的研究热点(张旗和周永章, 2017).尤其是机器学习的一个分支——深度学习(Deep Learning,DL)(Schmidhuber, 2015; Lecun et al., 2015)或称深度机器学习(Deep Machine Learning),在不适定反问题方面取得了引领性的进展(Girshick et al., 2014; Russakovsky et al., 2015; Krizhevsky et al., 2017).DL是一种深度的神经网络,能够用非监督式或半监督式的特征学习和分层特征提取高效算法来代替手工获取特征(王昊等,2020).DL相比传统的ANN具有更多的隐含层和更强的复杂函数逼近性能(Hornik et al., 1989; Lecun et al., 2015),DL与地球物理反演方法具有类似的优化算法(Kim and Nakata, 2018),极有助于不适定反问题的求解(Jin et al., 2017; Liu et al., 2020),也将在地球物理的海量数据反演中取得巨大的优势(王昊等, 2020).
目前,深度学习在地球物理反演中的应用大都是在电磁数据及地震数据处理领域.最新的研究如:王鹤等(2018)利用遗传神经网络实现了大地电磁反演,并验证了该算法的可行性和有效性;Puzyrev(2019)利用全卷积神经网络(Fully Convolutional Neural Networks,FCN)对井中垂直磁偶极子源发射地面接收的电磁数据进行二维反演;Puzyrev和Swidinsky(2020)将DL应用于海洋频率域可控电磁数据的一维反演,其结果表明,在浅层存在异常体时,深度学习反演相比传统反演,其不会影响深层的目标探测,具有较高的分辨率;Noh等(2020)实现了频率域航空电磁数据卷积神经网络(Convolutional Neural Networks,CNN)一维反演,结果表明CNN在合成数据量较少时其反演结果仍然具有较高的分辨率;Liu等(2020)提出了一种基于平滑约束和深度加权的直流电阻率FCN反演方法,有效的提高了解的分辨率;Li等(2020b)利用FCN直接从地震记录数据重建速度模型,其“端到端”的反演思路验证了DL在地球物理反演方法中的有效性;奚先和黄江清(2018)实现了散射波场的CNN反演成像方法,该方法具有良好、稳定的反演能力和泛化能力.此外,基于DL的地震全波形(Moseley et al., 2019; Zhang and Alkhalifah, 2019; Sun and Demanet, 2020)反演研究也取得了良好的进展.这些研究为重磁反演带来了更为广泛的应用前景.
基于此,本文提出一种基于DL的重力及重力梯度数据联合反演的方法.反演流程包括三个阶段:样本数据集生成,网络模型训练和利用网络模型进行预测.前两个阶段计算耗时较长,因为必须在足够大的训练集上训练网络模型,才能使网络模型具有泛化新数据的能力,但前两个阶段仅执行一次.反演预测较为迅速,通常在几十毫秒内完成.针对反演第一阶段,本文首先提出了一种重力及重力梯度空间域快速正演方法,以此来快速构建样本数据集;对于DL学习的网络结构,本文基于U-net网络结构(Russakovsky et al., 2015)建立重力数据(输入)到剩余密度模型(输出)的非线性映射网络结构,即三维重力场反演的“端到端”网络结构,本文称为GraInvNet (Gravity Inverse Net)网络结构;然后利用样本数据集对网络进行监督学习(训练),最后利用GraInvNet网络对理论数据和实测重力及重力梯度数据进行反演,以此来检验文中方法的可行性和有效性.
1 重力及重力梯度空间域快速正演
利用地下半空间模型的重力及重力梯度正演计算生成样本数据集,以及扩大样本数据集是减少DL反演过拟合的有效方法.因此,本文提出一种快速的重力异常及重力梯度异常的正演计算方法,以此来高效构建样本数据集,从而提高方法的实用性.
1.1 正演计算表达式
通常重力及重力梯度的正演计算是将地下半空间剖分成若干个规则长方体模型单元(如图1a所示),然后计算每一个长方体模型单元对观测点的异常(图1b),再将所有长方体模型对观测点的异常求和,即为地下半空间整个模型体对观测点的异常.
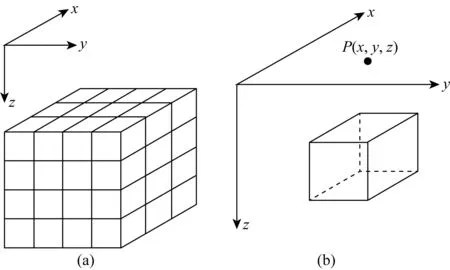
图1 地下半空间剖分模型单元示意图(a) 剖分单元示意图; (b) 长方体模型单元.Fig.1 Sketch map of partition model of underground half-space subdivision(a) Sketch map of subdivision element; (b) Prism model element.
单个长方体模型单元相对观测点P(x,y,z)的重力异常及重力梯度异常正演计算理论表达式如下(Li and Chouteau, 1998; 舒晴等, 2015):
(1)
(2)
(3)
(4)
(5)
(6)
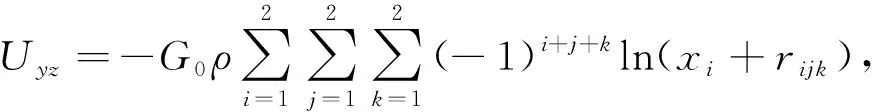
(7)
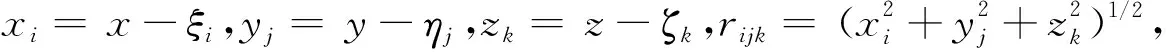
1.2 等效存储网格点几何格架技术
姚长利等(2003)提出了几何格架技术进行了重力异常的空间域快速正演计算,取得较好的效果.本文在此基础上提出一种网格点几何格架技术,此技术能够对已有的正演算法进行加速.以重力异常的正演计算为例进行说明,公式(1)可以写成如下表达式:
(8)
其中,
Q(xi,yj,zk)=-G0[xiln(yj+rijk)+yjln(xi+rijk)
(9)
与物性无关,本文称为网格点几何格架函数.网格点几何格架函数与文献(姚长利等, 2003)类似的几何格架函数:
S(xi,yj,zk)=
(10)
存在如下关系:
(11)
分析得出:(1)几何格架S与网格点几何格架Q的区别在于,前者是观测点相对于长方体模型单元的概念,后者是观测点相对于地下半空间的模型剖分网格点的概念;(2)几何格架S与网格点几何格架Q都具有平移等效性,重力异常Δg及重力梯度张量Uzz的几何格架S具有互换对称性;(3)几何格架S值是长方体模型单元8个顶点的网格点几何格架Q的代数和;(4)直接计算不同几何格架S的值存在8次(图2)计算同一网格点几何格架Q值的过程(边界除外).

图2 长方体模型单元共用网格点几何格架示意图Fig.2 Sketch map of geometric grid of common grid points of prism model elements
基于以上分析,本文对部分观测点网格点几何格架Q的值进行计算、存储,其余观测点网格点几何格架的值通过平移等效性进行调用,而不需要计算与存储,从而通过公式 (8)完成正演计算.
1.3 计算步骤
下面给出基于网格点几何格架的重力及重力梯度异常的空间域快速正演算法具体步骤.
步骤1:将地下半空间长方体模型单元的剖分与计算点相对应(图3所示),即计算点与地下半空间模型单元的网格点一一对应.并将计算点位置换算成实际里程,对长方体模型单元的剩余密度进行赋值;
步骤2:分别计算地下半空间内所有网格点对长方形观测区4个顶点的重力异常或重力梯度异常的网格点几何格架值(分别记为Q1,Q2,Q3及Q4.图3所示),并存储待后续计算调用;
步骤3:根据计算点与任意单一长方体模型单元8个顶点之间的相对位置关系,利用平移等效性调取其相对应的网格点几何格架值,再依据公式 (8)计算该长方体模型单元对计算点的重力异常或重力梯度异常;
步骤4:利用步骤3计算地下半空间每一个长方体模型单元对某一计算点的重力异常或重力梯度异常,最后求和得到该计算点总的重力异常或重力梯度异常;
步骤5:对步骤4遍历循环观测区,最终获得地下半空间剩余密度体在观测区的重力异常或重力梯度异常.
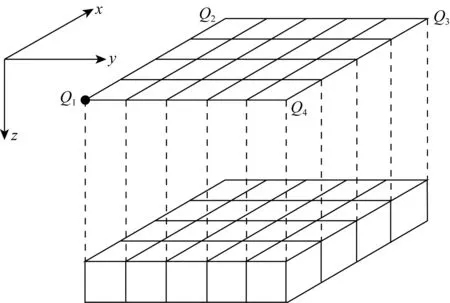
图3 计算点与网格点一一对应关系Fig.3 The corresponding relation between calculation points and grid points
2 深度学习反演
2.1 方法
目前DL网格结构主要有CNN、深度置信网络(Deep Belief Network, DBN)、循环神经网络(Recurrent Neural Networks, RNN)及生成对抗网络(Generate Adversarial Network, GAN)等,其余网络结构都是在此基础上改进而来.而应用最为广泛的是CNN,CNN在大型图像处理方面取得了一系列新的突破(Krizhevsky et al., 2017),其网络结构具备较强泛化能力和较好的迁移能力,以及健壮性也会更加优质(LeCun et al., 2015),尤其是FCN作为特殊的一种CNN其在医学图像语义分割方面(Russakovsky et al., 2015)显现出超越性的优势.
本文将观测平面上的多元重力数据视为二维图像的像素数据,作为FCN网络模型的输入端,将已知的地下模型作为训练标签,并在搭建的FCN网络模型上进行监督学习(训练),最终通过训练完成的FCN网络模型对重力数据进行反演.这一点本文反演方法与图像语义分割类似,但也存在差别.图像语义分割(图4a、b)的输入与输出的空间维度相同,本文反演方法的输入与输出的空间维度(图4c、d)不同,即输出端的剩余密度为三维数据(图4d)(地下半空间异常体物性值),输入端重力场响应为二维数据(图4c).因此,本文FCN网络结构的输出端采用多通道二维数据来连接分类模型,即将地下半空间每一深度层的物性值看作为自然图像的二维像素数据,多通道的通道数为反演深度的网格单元数.

图4 FCN端对端示意图(a)与(b)分别为图像分割的输入与输出示意图,(c)与(d)分别为本文方法的输入与输出示意图.Fig.4 Sketch map of FCN end-to-end(a) and (b) are the input and output schematic of image segmentation, (c) and (d) are the input and output schematic of the method proposed in this paper respectively.
地下半空间存在的密度异常体会在观测面上引起重力场响应,不同异常体引起的重力场响应也表现出不同特征(图4c、d).即具有一定的空间相关性和局部存在性,此特征也可以从极为发展的位场边缘识别技术(王万银, 2010;Wang et al., 2009, 2010)得到印证.总之,位场数据反演的输入和输出有两个特点:(1)空间的对应性,(2)局部的存在性.而FCN方法作为一种特殊的DL方法,其利用卷积算子代替矩阵相乘,重点学习输入图像与输出标签的局部性和空间性(Shi et al., 2019).因此,利用FCN方法对重力数据进行反演是切实可行的.
相同大小的异常体位于两个邻近垂直位置时,其引起的重力异常变化较小,FCN的网络结构需要具有足够的深度才有可能将其区分.然而,网格结构加深则会造成训练难度增加,诸如反向传播梯度消失、计算量增加等.因此,有必要将以高频信息为主的重力梯度异常作为以低频信息为主的重力异常的补充,共同作为FCN的输入端,可以增加同大小异常体位于两邻近垂直位置时的重力场响应差异,从而进一步提高FCN的预测精度.换言之,在不增加感受野的前提下,提高位置相似异常体的重力响应的辨识度来进行FCN网络训练,以此提高其预测的精度.本文反演的目标是通过FCN的方法得到重力异常和重力梯度异常到异常体剩余密度的映射函数:
ρ=F(Δg,Uxx,Uxy,Uxz,Uyy,Uyz,Uzz).
(12)
2.2 网络结构
Long等(2015)提出了FCN方法,该方法是将CNN方法的全连接层修改为卷积层,实现了端到端的学习.FCN方法相比传统的CNN方法,其优点一是节点超参数大大减少从而提高计算效率,二是避免全连接层数据一维化而丢弃信息,三是“跳跃结构”(Russakovsky et al., 2015)融合了低中高阶特征信息,进一步优化了输出结果,以此可以高效进行密集型像素的预测.本文基于FCN方法的U-Net架构设计重力场数据反演的网络结构(GraInvNet),如图5所示.GraInvNet是U-Net的一种简化与改进,简化了网络结构的深度及卷积通道数,改进了输出端的标签分类(图4d),以及当输入与输出在不同空间维度时,利用第一次卷积进行裁剪或填充,以便跳跃链接时编码层与解码层的组合.GraInvNet有15层采用卷积运算(宽度为3,跨度为1),3层采用最大池化运算(宽度为2,跨度为2),其感受野为80(计算方法参照Luo 等(2017)文献),这对于本文重力场输入数据空间维度的反演任务来说,非线性逼近程度已足够大.
2.3 正则化
在DL中,泛化能力是指已完成训练的网络结构对未泄露数据的预测性能(Zhang et al., 2018; Chan et al., 2017).在实际情况中,我们通常将样本数据集按照一定比例分成两部分,大部分用来训练,小部分未泄露数据进行测试,最后通过测试误差来评价方法的泛化能力.决定DL反演成败的两个关键因素是(1)降低训练误差和(2)减少训练误差与测试误差之间的差距.训练误差较大对应为欠拟合,可以更改FCN网格结构或训练算法来完善,训练误差和测试误差之间的较大差距对应过拟合.在数据量充足的情况下正则化方案是解决过拟合的一种有效方法.
Dropout是深度学习模型训练中最简单、最常用的正则化技术(Hinton et al., 2012b).Dropout是指在每一轮训练中按一定比例随机丢弃部分网络神经单元之间的链接(Srivastava et al., 2014; Krizhevsky et al., 2017),避免训练数据在所有节点进行训练,该策略减少了网络单元之间复杂的共适应关系,同时也对网络单元起一定的平均作用,故而可减少过拟合.此外,本文对于GraInvNet网络结构,不仅在卷积层后使用Dropout,还在卷积层间使用批处理归一化的正则化方案.该方案的优势是在FCN网络训练期间性能更稳定(Ioffe and Szegedy, 2015; He et al., 2016; Puzyrev, 2019).
2.4 损失函数
损失函数是DL网络训练过程的指挥棒,其通过正向传播的输出结果与样本标签值之间的误差反向传播来修改网络单元节点权值及其他参量,本文指通过预测地下半空间长方体模型密度与已知模型密度的误差进行调参.常用损失误差为L1、L2范数,其表达式分别为
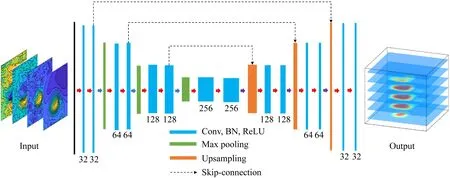
图5 GraInvNet网络结构由3个下采样层和3个上采样层组成,下采样和左侧卷积层对应编码阶段,上采样和右侧卷积层对应解码阶段,图中黑色数字表示特征图的通道数,Conv为卷积,BN为批归一化,ReLU为激活函数,Max pooling为最大池化,Upsampling为上采样, Skip-Connection为跳跃链接.Fig.5 GraInvNet architectureIt is composed of three down-sampling layers and three up-sampling layers. The down-sampling layer and the left convolution layer correspond to the encoding stage, the up-sampling layer and the right convolution layer correspond to the decoding stage. In the figure, the black number indicates the number of channels in the feature map, Conv is convolution, BN is batch normalization, ReLU is activation function.
(13)
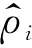
GraInvNet网络模型训练的实质就是损失函数数学期望极小化的过程.传统地球物理反演的实质是目标函数极小化的过程.其实两者的二范数表达式类似,区别在于传统反演目标函数是预测数据的正演响应与实测数据的二范数或其正则化改进,且该目标函数极小化过程的计算成本极为昂贵,而DL损失函数极小化过程效率较高.本文采用归一化数据的L2范数作为损失函数.
2.5 学习算法的选择
强大的学习算法是提高深度学习反演性能必不可少的步骤,通过GraInvNet网络学习算法一步步的迭代使损失函数极小化,达到全局的最优值.
随机梯度下降法(Stochastic Gradient Descent,SGD)是一种高效的优化方法,是DL中最有效的核心算法之一(Hinton et al., 2012a; Deng et al., 2013; Hinton and Salakhutdinov, 2006; Krizhevsky et al., 2017).然而SGD选取一个样本数据作为其梯度方向时,其方向具有随机性,极有可能不能较快收敛到最优解.此外,SGD算法的学习率是全局统一的,而待优变量对于损失函数的依赖却各不相同,因此其取值不当易造成部分变量收敛速度慢及部分变量的收敛过程产生震荡.针对SGD固定的学习率问题,AdaGrad (Adaptive Gradient)算法将每一个变量采用不同的学习率,自适应进行学习率的调整.但该算法存在一个平方梯度迅速积累而造成学习速度下降的问题,从而阻止训练模型达到局部极小值.RMSProp (Kingma and Ba, 2014)是AdaGrad的改进算法,其采用平方梯度累积指数衰减的动态平均算法,使得模型训练得以继续.考虑到动量法具有对梯度算法加速的优点,本文采用Kingma和Ba(2014)提出的ADAM算法(Adaptive Moment Estimation),它是动量法与RMSProp算法的结合,适合大数据量超参数的优化问题,并具备计算效率高收敛速度快的优势.
2.6 网络规格及调参
激活函数选用CNN以及其他DL类型最常用的线性整流函数(ReLU,见公式(14))及其改进函数(Xu et al., 2015),其主要优势是稀疏性,能够减少梯度消失的可能性,还具有非常好的收敛性能和较低的计算成本.输出选择S型函数(见公式(15)).此外,鉴于在图形特征提取中最大值池化相比平均值池化具有一定优势(Boureau et al., 2010),本文GraInvNet网络选用最大值池化方案.
fReLU(t)=max(t,0),
(14)
fsigmoid(t)=1/(1+e-t).
(15)
在调参方面需要考虑到训练轮数、样本批量数以及Dorpout的比例等因素对模型性能的影响.以上因素需兼顾计算效率和精度,从而优化GraInvNet网络结构,最终的训练完成的GraInvNet具备计算的准确性,同时也需对新样本具备一定的泛化性.
3 理论模型试验
3.1 样本数据集的构建及训练
将地下半空间划分为40×40×20个长方体模型单元,如图1a所示,其中长方体模型单元大小为100 m×100 m×50 m,模拟观测数据区大小为4 km×4 km,计算的单通道(重力异常或某种分量重力梯度异常)正演数据为41×41个.样本数据集的构建首先是将多个长方体模型单元组合为一定规模的长方体模型块体或台阶模型,如8个长方体模型单元组合为2×2×2长方体模型块体,64个长方体模型单元组合为4×4×4长方体模型块体等;随后将不同大小的长方体模型块体分别设置在地下半空间不同位置,再利用本文第1节提供的快速正演方法获取其重力异常及重力梯度异常数据,其中剩余密度大小为1.0 g·cm3;最后对归一化后正演数据作为样本数据集中的输入数据,不同位置处的密度归一化后作为标签.样本数据集总共包含了14696对不同组合模型块体正演数据,单个样本数据输入端包含7个通道,即Δg,Uxx,Uxy,Uxz,Uyy,Uyz和Uzz异常,数据规格为41×41×7,输出端为40×40×20,即地下半空间长方体模型单元的个数.
由于重力异常及重力梯度异常的正演为线性关系(式(1)—(7)),故可利用已正演的样本数据进行不同密度大小的样本数据扩充,如本文剩余密度大小为-1.0 g·cm3的样本数据是直接扩充而获取的,加上正演数据集,共计29392个样本数据.将样本数据划分为训练数据、测试数据以及验证数据,其对应比为18∶1∶1,即训练数据集包含26452个样本数据,而验证和测试集各有1470个样本数据.
训练轮数为100,每次训练后进行一次验证,图6所示为本文所提GraInvNet网络的训练误差与验证误差,可以看出,模型训练良好,未出现过欠拟合.
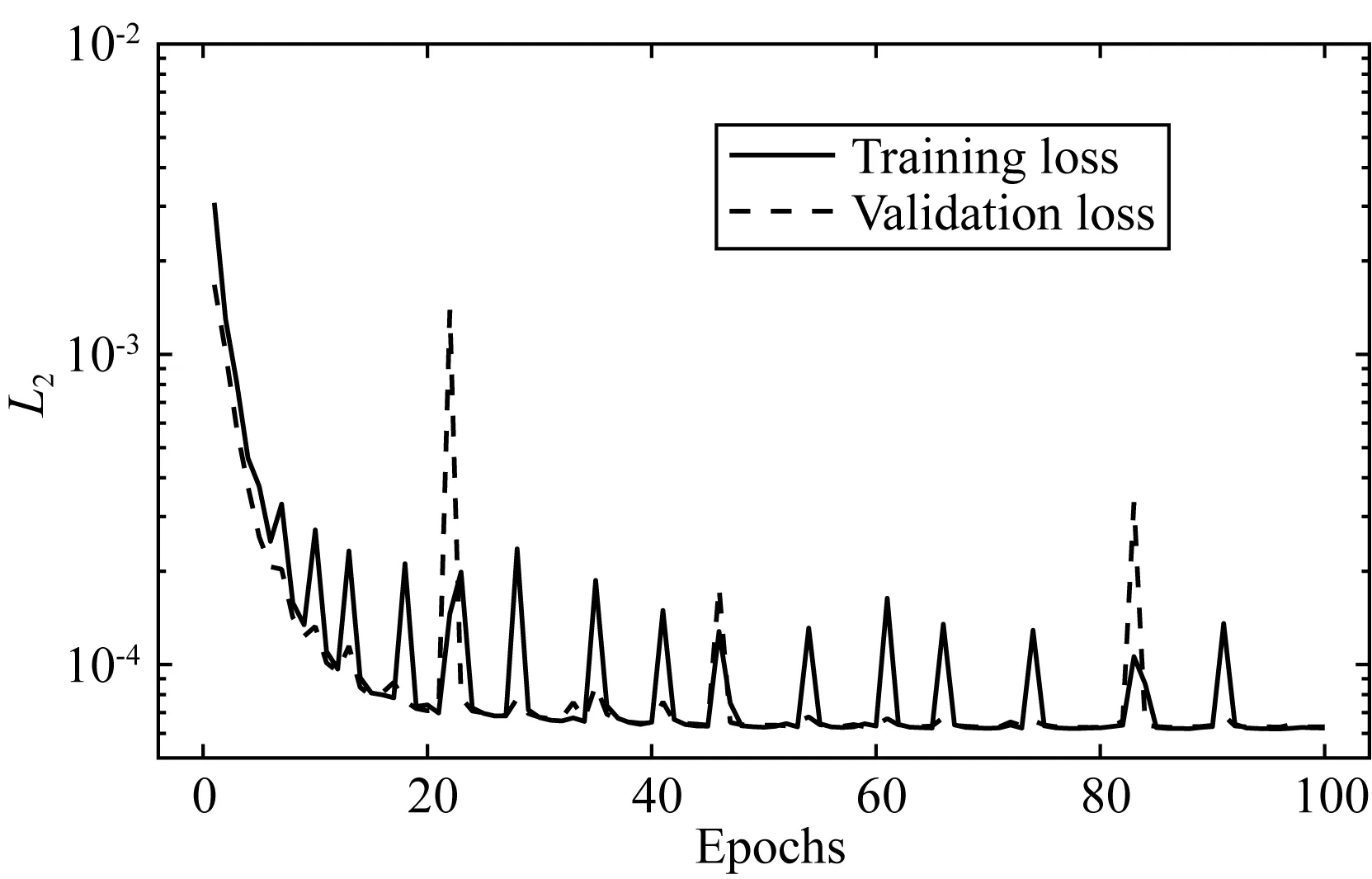
图6 GraInvNet训练误差及验证误差Fig.6 Training error and validation error of GraInvNet
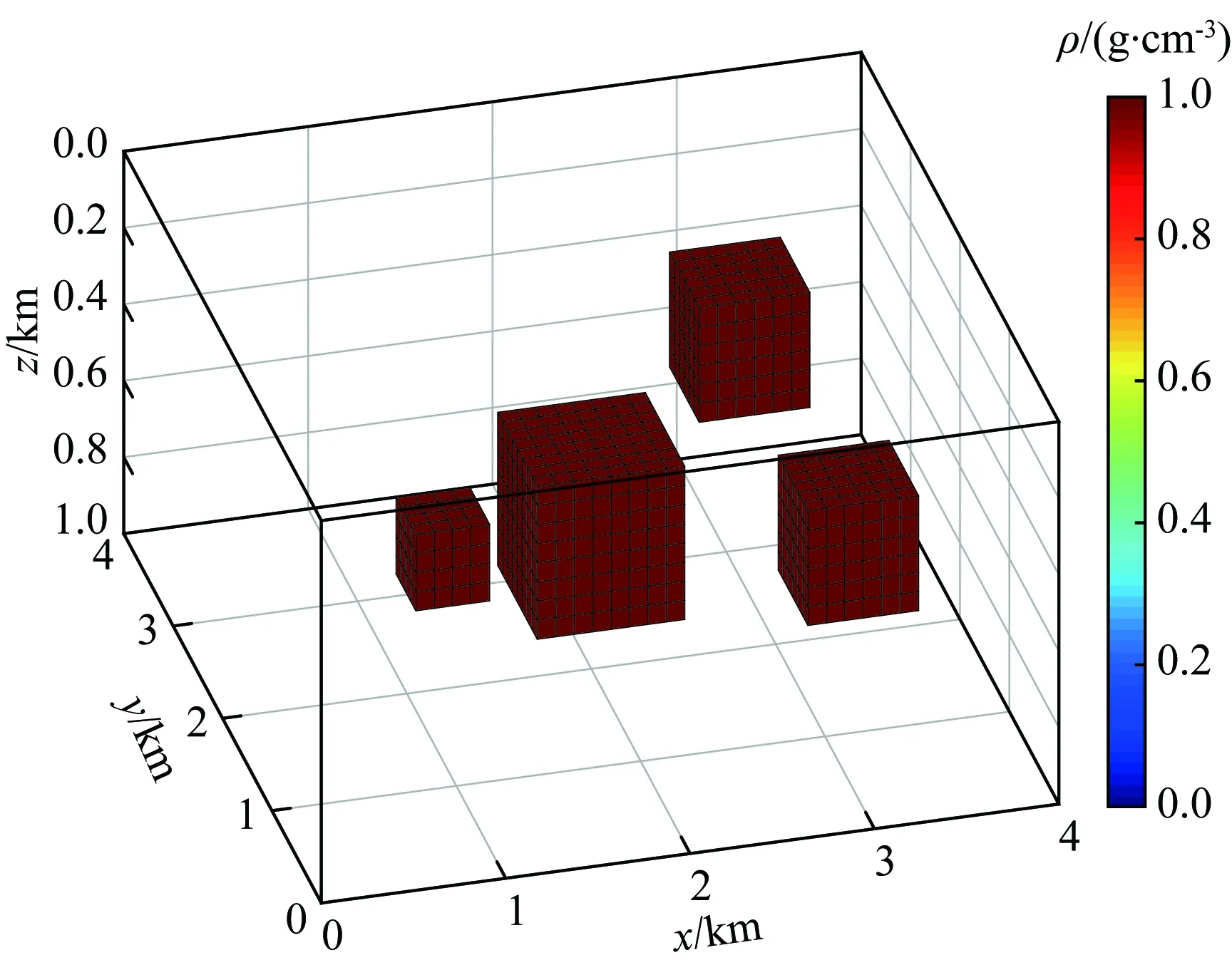
图7 组合模型透视图Fig.7 Perspective view of combination model
3.2 组合模型一
长方体组合模型一由4个不同大小长方体模型组成,如图7所示,长方体剩余密度都为1.0 g·cm-3.其余参数见表1.利用文中已训练完成的GraInvNet网络对组合模型一分别进行重力异常反演、重力异常与部分重力梯度异常联合反演以及重力异常与全部重力梯度异常联合反演的三种反演方案进行对比,其结果如图8a、b及c所示.可以看出在无噪声情况下,重力异常反演结果(图8a)能够“聚焦”于真实模型,表明本文GraInvNet网络不仅可以有效的对重力异常进行反演,而且还说明了对单一块体模型所构建的样本数据集进行训练,可对类似块体的组合模型进行预测,验证了FCN的卷积核具有局部性和权值共享的特点和优势,从而表明了本文GraInvNet网络所具备的泛化性能.但同时也可以看出单独重力异常反演结果的边界不够清晰,而重力异常与部分重力梯度异常组合的多维度信息作为GraInvNet网络的输入端进行反演,其结果(图8b)拟补了重力异常反演结果边界模糊的劣势,重力异常与全部重力梯度异常的联合反演结果(图8c)边界更为清晰,精度更高,与理论模型轮廓保持高度一致,说明了基于DL的多维度联合反演精度相比单一的重力异常反演结果精度高.
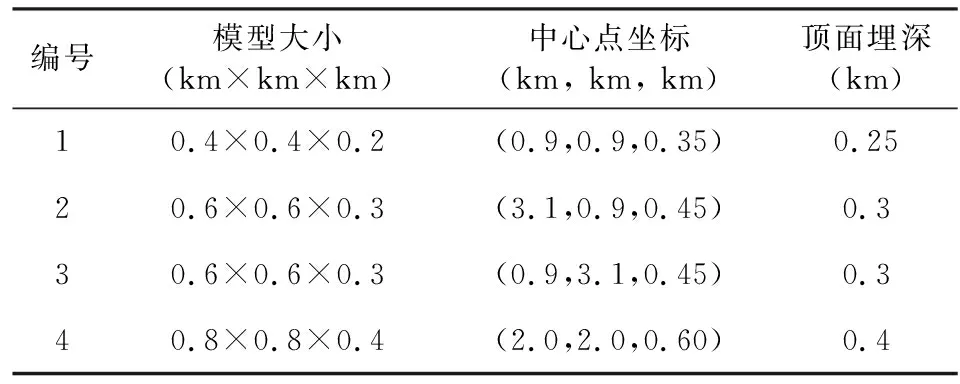
表1 长方体模型参数Table 1 Cuboid model parameters
为了更加贴合实际资料处理,对重力异常及重力梯度异常分别加入其最大值10%的随机噪声,并对其进行反演,结果如图8d、e及f所示.可以看出,含噪声重力异常反演结果(图8d)虽然可以反映出异常体的位置,但相比无噪声情况下重力异常反演结果(图8a),其效果较差;含噪声的重力异常与部分重力梯度异常的联合反演结果(图8e)对比无噪声情况下的反演结果(图8b)同样受到一定的影响,但联合反演相比单独重力异常反演结果其在边界处的影响更小,联合反演的结果可以准确的反映出异常体的轮廓.含噪声重力异常与全部重力梯度异常的联合反演结果(图8f)基本上与无噪声情况下的反演结果(图8c)一致.以上说明了基于DL的多维度联合反演具有一定抗噪声性能,计算稳定性较高.
为了进一步对比三种反演方案的优劣,给出了坐标点(0 km,0 km)至坐标点(4 km,4 km)剖面的切块图(图9),以及z=0.40~0.45 km反演结果水平切块图(图10).可以看出无噪声情况下重力异常反演结果纵向分辨率较差(图9a),横向分辨率相对较好,但也存在边界的模糊性(图10a,编号为4的异常体).含噪声情况下重力异常反演结果横纵向分辨率都变差,横向的边界不够清晰(图10d),异常体的纵向埋藏深度出现较大的偏差(图9d,编号为1和2的异常体).这是由于重力异常为低频信息,同姿态同大小的异常体埋深极为相近时,其在观测面引起的重力异常变化较小,一方面,随机噪声的大小极有可能大于其垂向相邻异常体在观测面上重力异常的变化,从而造成GraInvNet网络预测结果存在深度上的偏差;另一方面如果采用DL去准确区分观测重力异常差异较小的垂向相邻异常体时,则需要更深的网络结构和更高的计算成本;此外,为了防止过拟合则需要更广泛和更充足的样本数据集,从而进一步增加训练难度和成本.因而,为了提高DL的反演的精度,极为有必要增加同姿态同大小异常体位于相近位置时重力场响应的差异.而多维度重力梯度异常和重力异常能够多角度增加异常体响应的辨识度,其全方位的重力场响应数据作为DL的训练样本数据,在一定程度上会减少“盲人摸象”的困境,进一步溯源求真.如图9b、e与图10b、e所示的部分重力梯度异常联合反演结果相比重力异常的反演结果在纵向上的精度大大提高,重力异常与全部重力梯度异常的联合反演结果(图9c、f与图10c、f)更为精确,横纵分辨率高.

图8 反演结果三维透视图(a)、(b)及(c)分别为无噪声情况下Δg、Δg & Uxz & Uyz & Uzz与Δg &全部分量反演结果,(d)、(e)及(f)分别为含噪声情况下Δg、Δg & Uxz & Uyz & Uzz与Δg &全部分量反演结果.Fig.8 3D perspective views of inversion result(a), (b) and (c) are the inversion results of Δg, Δg & Uxz & Uyz & Uzz and Δg & all components in the absence of noise, respectively; (d), (e) and (f) are the inversion results of Δg, Δg & Uxz & Uyz & Uzz and Δg & all components in the presence of noise, respectively.
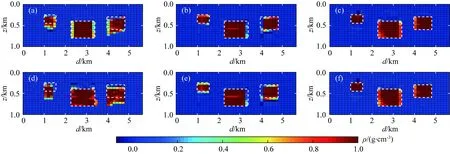
图9 反演结果切块图(a)、(b)及(c)分别为无噪声情况下Δg、Δg & Uxz & Uyz & Uzz与Δg &全部分量反演结果;(d)、(e)及(f)分别为含噪声情况下Δg、Δg & Uxz & Uyz & Uzz与Δg &全部分量反演结果;切块线首尾坐标分别为(0 km,0 km)和(4 km,4 km),白色虚线框为模型体的边界位置.Fig.9 Block diagram of inversion result(a), (b) and (c) are the inversion results of Δg, Δg & Uxz & Uyz & Uzz and Δg & all components in the absence of noise, respectively; (d), (e) and (f) are the inversion results of Δg, Δg & Uxz & Uyz & Uzz and Δg & all components in the presence of noise, respectively; The first and last coordinates of the cutting line are (0 km,0 km) and (4 km,4 km),the white dotted box indicates the boundary position of the model.
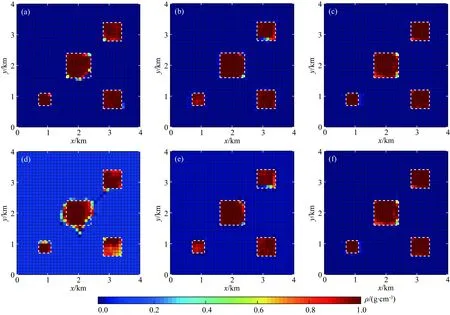
图10 z=0.40~0.45 km反演结果切块图(a)、(b)及(c)分别为无噪声情况下Δg、Δg & Uxz & Uyz & Uzz与Δg &全部分量反演结果;(d)、(e)及(f)分别为含噪声情况下Δg、Δg & Uxz & Uyz & Uzz与Δg &全部分量反演结果;白色虚线框为模型体的边界位置.Fig.10 Block diagram of inversion result at z=0.40~0.45 km(a), (b) and (c) are the inversion results of Δg, Δg & Uxz & Uyz & Uzz and Δg & all components in the absence of noise, respectively; (d), (e) and (f) are the inversion results of Δg, Δg & Uxz & Uyz & Uzz and Δg & all components in the presence of noise, respectively;the white dotted box indicates the boundary position of the model.
为了进一步说明联合反演结果与理论异常的拟合程度,文中分别将无噪声与含噪声数据的反演结果进行正演,其正演重力异常结果与理论异常的残差值如图11所示,重力异常与重力梯度异常残差的标准差与随机噪声标准差见表2.无噪声情况下重力异常差值的最大最小值分别为0.912、0.015 mGal,含噪声情况下重力异常差值的最大最小值分别为1.613、0.008 mGal,经对比分析各分量的方差及标准差,表明文中所述反演方法的精度高.
3.3 组合模型二
组合模型二为四层台阶与长方体的组合模型,如图12所示,其中四层台阶模型的每层台阶大小相同都为1.4 km×0.6 km×0.15 km,每层台阶的中心坐标分别为(2.0 km,0.9 km,0.275 km)、(2.0 km,1.2 km,0.425 km)、(2.0 km,1.5 km,0.575 km)及(2.0 km,1.8 km,0.725 km),长方体大小为0.8 km×0.5 km×0.3 km,长方体顶面埋深为0.2 km,中心点坐标为(2.0 km,3.05 km,0.35 km),四层台阶与长方体剩余密度都为1.0 g·cm-3.组合模型二相比组合模型一的变化是加入新类型模型——台阶,以及样本数据集中未包含的长方体模型.利用本文的GraInvNet网络对组合模型二的重力异常及全部重力梯度异常进行联合反演,其结果如图13所示,可以看出台阶模型的反演结果与真实模型高度吻合,其幅值在深部处略有差别(图13c),长方体模型在深部的幅值也略有差别(图13e及f),其余部分也与理论模型高度吻合.表明GraInvNet网络可以对与样本模型相似组合模型的异常体进行精确定位,同时也可以准确地预测出模型值的大小,表明其反演能力很好.为了更加直观地了解反演结果中异常体的位置、形状和物性值,图13a、b、c与d 分别给出不同方向的反演切块图,可以看出反演结果与真实模型的边界及形状吻合,并且反演结果的幅值大小也与已知模型接近.
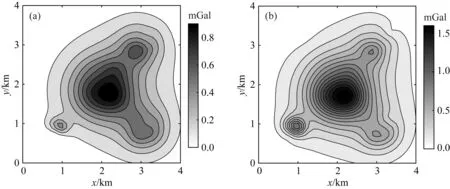
图11 重力理论异常与预测结果正演的残差(a)无噪声情况; (b)含噪声情况.Fig.11 The residuals of theoretical gravity anomaly and forward value of prediction result(a) Free noise situation; (b) Noise situation.
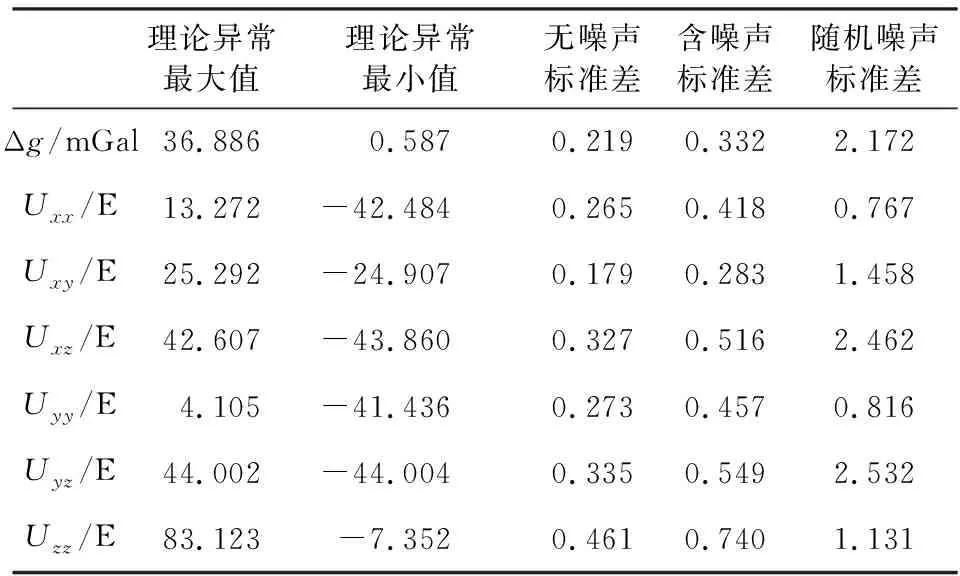
表2 理论异常最大最小值、反演结果拟合残差的标准差及随机噪声标准差Table 2 The maximum and minimum value of theoretical anomaly, the standard deviation of the fitting residuals of inversion result and random noise

图12 组合模型透视图Fig.12 Perspective view of combination model
同时为了更加贴合实际资料处理,对重力异常及重力梯度异常分别加入其最大值10%的随机噪声,再对其进行反演,结果如图14所示.可以看出,除去异常体部分边界位置的幅值略有差异(图14c、e及f),其余部分也与理论模型高度吻合,表明GraInvNet网络反演的稳定性较高,具有一定的抗噪声能力.
为了进一步说明联合反演结果与理论异常的拟合程度,文中分别将无噪声与含噪声数据的反演结果进行正演,其正演重力异常结果与理论异常的残差值如图15所示,重力异常与重力梯度异常残差的标准差与随机噪声标准差见表3.无噪声情况下重力异常差值的最大最小值分别为0.985、0.012 mGal,含噪声情况下重力异常差值的最大最小值分别为2.975、-0.864 mGal,经对比分析各分量的标准差与理论异常的大小,表明文中所述反演方法的精度高.
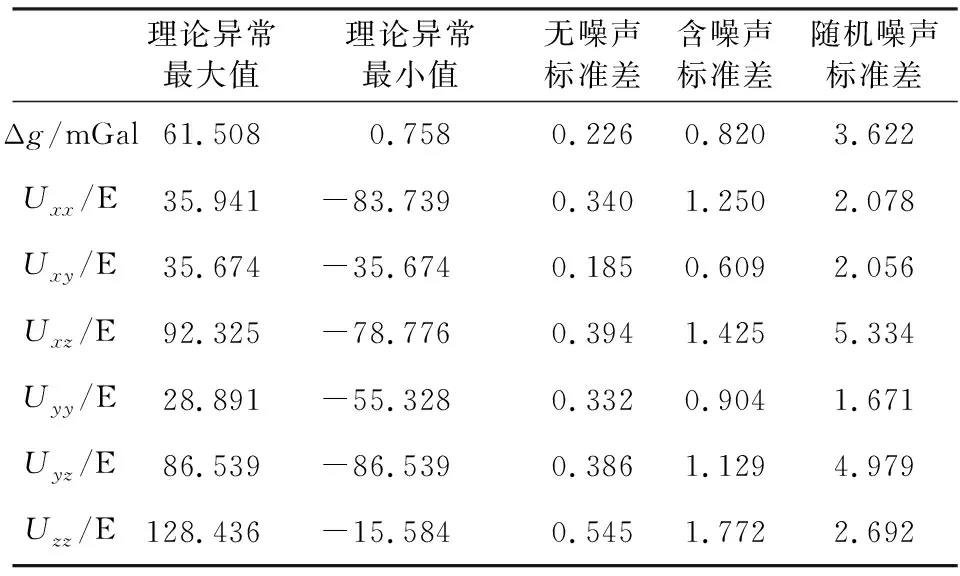
表3 理论异常最大最小值、反演结果拟合残差的标准差及随机噪声标准差Table 3 The maximum and minimum value of theoretical anomaly, the standard deviation of the fitting residuals of inversion result and random noise

图13 无噪声反演结果(a)、(b)、(c)及(d)分别为y=1.3~1.4 km、x=1.9~2.0 km、x=2.5~2.6 km及z=0.35~0.4 km的反演结果切块图,白色虚线框为模型体的边界位置,(e)、(f)为剩余密度大于0.1 g·cm-3的三维透视图.Fig.13 Inversion result in the absence of noise(a), (b), (c) and (d) are block diagrams of inversion results at y=1.3~1.4 km, x=1.9~2.0 km, x=2.5~2.6 km and z=0.35~0.4 km respectively, the white dotted box indicates the boundary position of the model, (e) and (f) are the three-dimensional perspectives, where residual density is greater than 0.1 g·cm-3.
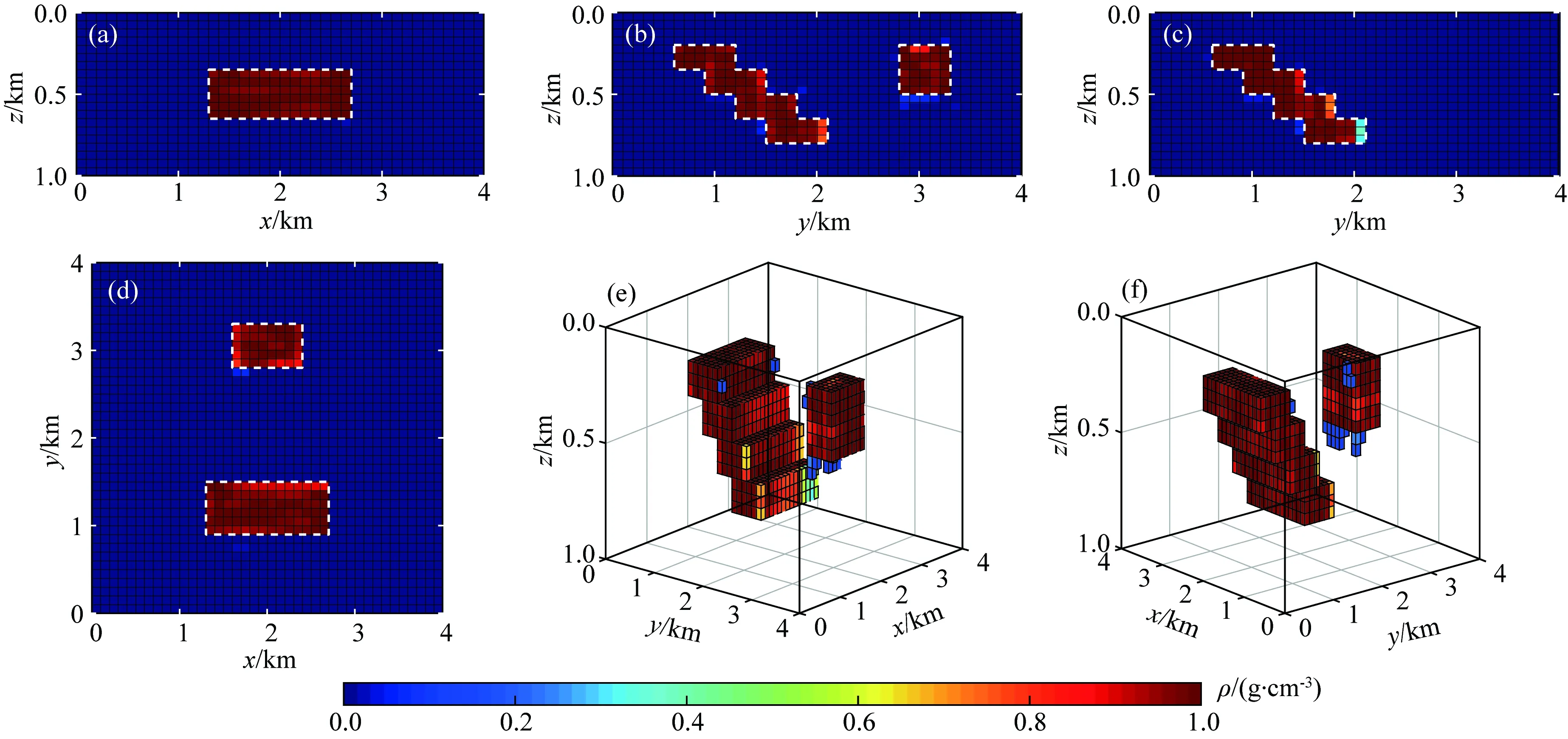
图14 含噪声反演结果图(a)、(b)、(c)及(d)分别为y=1.3~1.4 km、x=1.9~2.0 km、x=2.5~2.6 km及z=0.35~0.4 km的反演结果切块图,白色虚线框为模型体的边界位置,(e)、(f)为剩余密度大于0.1 g·cm-3的三维透视图.Fig.14 Inversion result in the presence of noise(a), (b), (c) and (d) are block diagrams of inversion results at y=1.3~1.4 km、x=1.9~2.0 km、x=2.5~2.6 km and z=0.35~0.4 km respectively, the white dotted box indicates the boundary position of the model, (e) and (f) are the three-dimensional perspectives, where residual density is greater than 0.1 g·cm-3.
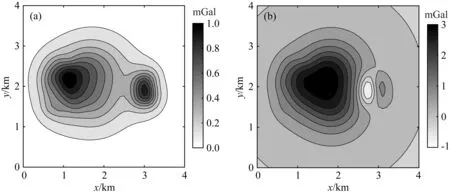
图15 重力理论异常与预测结果正演的残差(a)无噪声情况; (b)含噪声情况.Fig.15 The residuals of theoretical gravity anomaly and forward value of prediction result(a) Free noise situation; (b) Noise situation.
4 实际数据反演
采用本文的方法对美国路易斯安那州西南部Vinton盐丘的地面重力异常和航空重力梯度异常数据进行反演.盐丘构造的研究对于寻找油气区带及封闭圈具有非常重要的作用(贾承造等, 2003).Vinton盐丘是一个位于新生代和中生带晚期页岩砂岩中的浅层刺穿盐丘,是由一定规模的盐核和其顶部的盐丘帽组成,盐丘帽是由石灰岩、石膏、硬石膏和黏土组成(Coker et al., 2007).有较多钻孔穿过该盐丘,盐丘的成分、物性大小、空间分布状态资料较为详细(Ennen, 2012),因此,该地区的重力数据也被诸多学者用于检验重力数据处理方法的效果(Yuan et al., 2013;秦朋波和黄大年, 2016).
盐丘帽埋深大约位于地下200~650 m之间,密度为2.75 g·cm-3,周围围岩密度约为2.2 g·cm-3.因此,选择2.2 g·cm-3的密度对85 m高空处的FTG数据进行地形改正,以及对高频噪声进行抑制,其结果如图16a、b、c、d、e、f所示,同时采用插值分割法(徐世浙等, 2009)对地面重力异常数据进行局部重力异常的提取,其结果如图16g所示,以上预处理结果可以认为是由0.55 g·cm-3的剩余密度所产生.图中观测区大小为4.0 km×4.0 km,数据点距为100 m×100 m,共41×41个点,将地下半空间划分为40×40×20个长方体模型单元,其大小为100 m×100 m×50 m.
根据已知情况,并利用本文所提的GraInvNet网络对图16所示的数据进行预测,该过程对反演密度进行了约束,其范围为:-0.2~0.55 g·cm-3.最终反演结果如图17所示,从图17a、b可以看出岩丘帽中心深度大约为500 m,深度范围在300~700 m之间,东西向长约为1.2 km,南北向长约为1.1 km,这一结果与已知的地质信息较为吻合(Thompson and Eichelberger, 1928).从三维透视图(图17c、d)可以看出高密度的物性分布更为“聚焦”,近似为不规则椭球体,低密度至高密度过渡带范围较小,约为100 m间隔,表明密度较大值占反演结果的主要分布范围.
5 结论与讨论
本文提出一种基于DL的重力异常及重力梯度异常联合反演的新方法,该方法对应的DL网络结构称为GraInvNet.本文首先提出了一种快速正演计算方法对GraInvNet网络所需要的样本数据集进行高效构建,从而提高DL反演的实用性;然后,将样本数据输入到GraInvNet网络,以此来学习从正演数据到模型的复杂映射关系.在训练阶段,根据损失函数值与验证值的变化来优化网络结构、正则化方案等;最后,通过已训练完成的GraInvNet网络进行反演预测,此阶段可以达到高效的计算速度,通常几十毫秒就可完成.
组合模型一为样本数据集相同模型的组合,重力异常的反演结果能够“聚焦”于真实模型,且采用单一块体模型所构建的样本数据集对GraInvNet网络进行训练,该网络可对类似块体的组合模型进行预测,表明基于DL的重力异常反演所具有的可行性,以及本文GraInvNet网络所具有的较强泛化性.随着多维度重力梯度异常信息的加入,GraInvNet网络的反演结果精度显著提升,含噪数据试验表明GraInvNet网络具有较强的抗噪声性能.组合模型二为样本数据集的类型模型,GraInvNet网络的反演结果与理论模型高度一致,表明本文反演方法具有较强的泛化性能和鲁棒性.将文中的方法应用于实测的航空重力梯度异常和地面重力异常的联合反演,其结果与已知的地质情况吻合,表明本文的反演方法可以应用于实际数据.
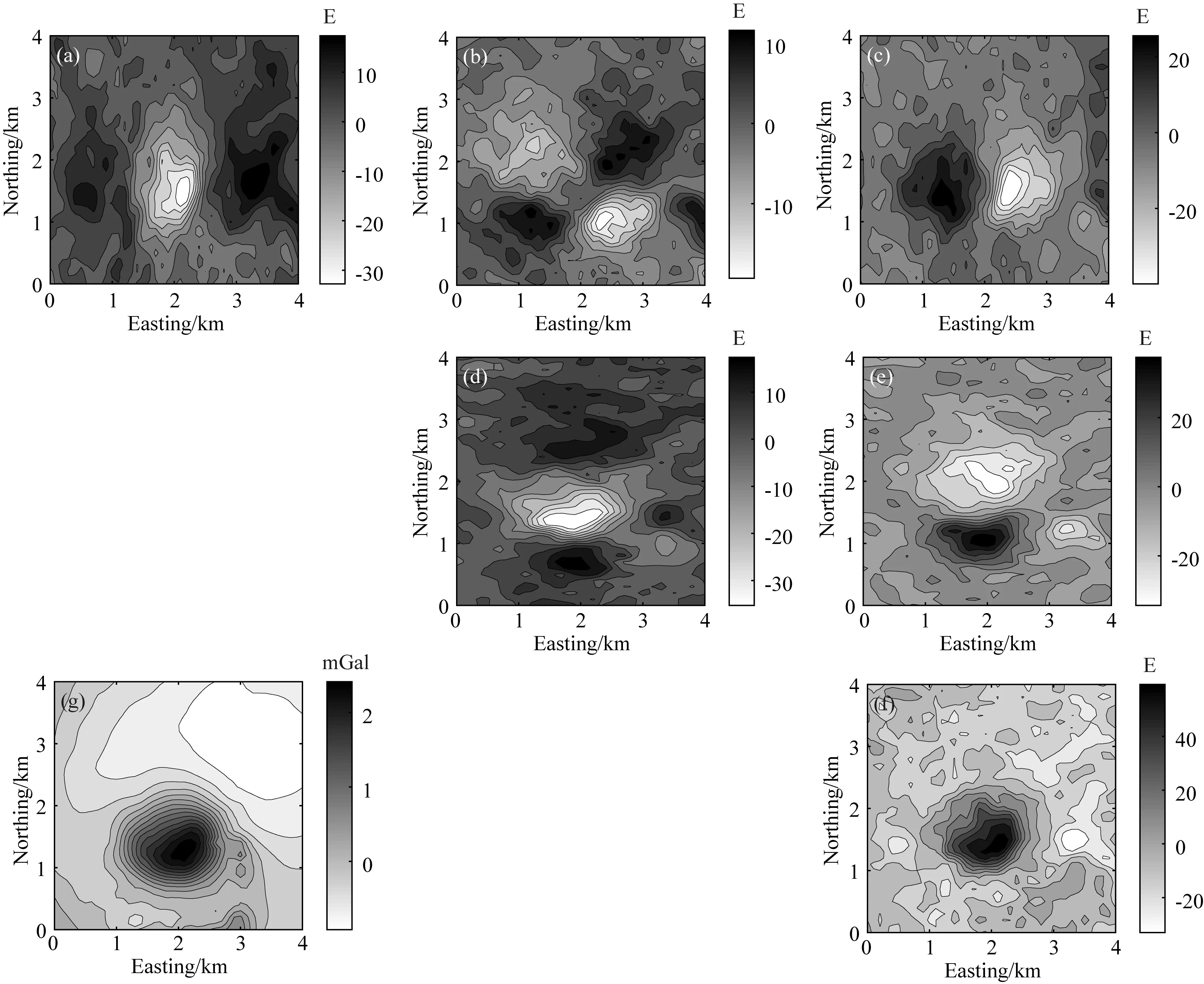
图16 Vinton岩丘实测重力数据(a)、(b)、(c)、(d)、(e)、(f)及(g)分别对应Uxx、Uxy、Uxz、ΔUyy、Uyz、Uzz与Δg分量.Fig.16 The measured gravity data of Vinton salt dome(a), (b), (c), (d), (e), (f) and (g) correspond to Uxx, Uxy, Uxz, ΔUyy, Uyz, Uzz and Δg components respectively.
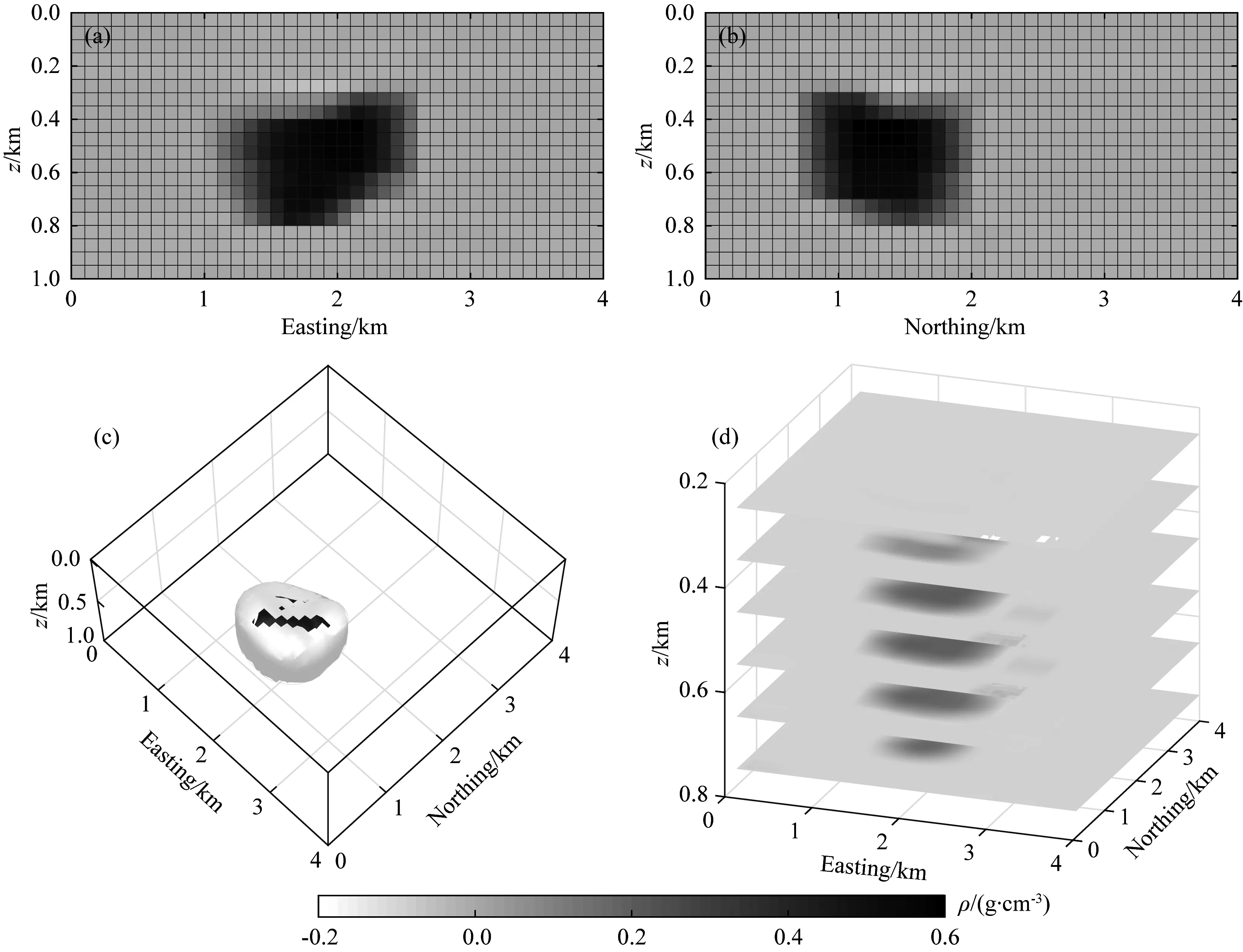
图17 Vinton岩丘实测数据反演结果(a)与(b)分别为南北向1.6~1.7 km与东西向1.9~2.0 km的反演结果切片图;(c)为反演密度分别为0.45、0.2 g·cm-3的包络曲面图;(d)为反演结果在深度方向上切片图,切片深度为250 m变化至650 m,间隔100 m.Fig.17 Inversion results of the measured data of Vinton salt dome(a) and (b) are slice maps of inversion results in north-south direction of 1.6~1.7 km and east-west direction of 1.9~2.0 km respectively; (c) is the envelope surface with inversion density of 0.45 and 0.2 g·cm-3 respectively; (d) is slice map of inversion results in depth direction with slice depth from 250 m to 650 m and interval of 100 m.
基于DL的重力反演实质上是利用FCN方法对地下半空间的剩余密度体的位置及物性大小进行分类预测,其“端到端”的网络结构也可以应用到其他地球物理反演中,如磁及磁梯度反演、电磁反演及面波波速反演等.另一方面,由于地球物理反演的复杂性,DL反演方法需具有的普适性在于如何构建一个足量的、多样性的、代表性的高质量样本数据集,然而,这势必会引起网络复杂度与计算量增加.因此,在下一步工作中,我们将进一步增加样本的多样性来提升复杂地质模型的反演效果,同时对网络结构与节点超参数进一步优化来提高训练效率和反演精度,从而使得基于DL学习的重力反演方法更加普适化与智能化.
致谢感谢Bell Geospace公司提供Vinton岩丘实测重力数据.非常感谢匿名审稿专家对论文提出的宝贵修改建议.

