高压下Nb3Sn 单晶的超导相转变

石震天，杨绪佳，王豪阳，乔 力

（太原理工大学机械与运载工程学院应用力学研究所，山西 太原 030024）

A15型Nb3Sn超导材料是制造高场(＞10 T)超导磁体线圈的主要材料，被广泛应用于磁约束可控核聚变和高能物理等强磁体领域[1-5]。力学变形诱导的 Nb3Sn材料超导电性能弱化是强磁场磁体制造需要解决的基础问题之一，研究高压下 Nb3Sn单晶的超导相转变行为对于揭示这一弱化机理具有重要意义。早期对于 Nb3Sn材料超导相转变行为的研究主要集中于工程用复合超导股线在力学载荷作用下超导临界性能参数退化的实验和表征[6-7]。基于此，发展了可用于磁体设计的经验标度关系[8-12]。伴随着强磁场制造水平的提升，需要进一步探究 Nb3Sn 材料超导相转变力学效应背后的物理机制。与 Nb3Sn复合超导股线相比，单晶体和多晶体的组织结构更简单，且更方便获得不同载荷模式下的电阻率变化规律，因此高压下 Nb3Sn单晶体的超导相转变受到了学者们的广泛关注。

式中： ρ0为材料的残余电阻率， ρ1、ρ2和T0均为根据实验结果拟合的参数。该模型形式简明，在18～850 K温度范围内与实验数据的误差小于1%。在Woodard-Cody 模型的基础上，Qiao 等[18]建立了 Nb3Sn超导材料常态电阻率经验模型，用以描述常态电阻率、三维应变和温度的耦合效应，模型预测结果与实验数据一致。这些经验模型通过简洁的数学公式很好地刻画了实验观测结果，但是缺乏对超导相转变附近正常态电阻率静水压效应机理的阐述。Webb 等[19]认为超导相转变附近常态电阻率的T2依赖特性是基于电子-声子散射产生的，但该理论不足以解释所有的数据，仍然需要继续探索载荷作用下电阻率T2依赖性的内在机制[20]。为理解这一效应，需要定量描述 Nb3Sn单晶体在高压和极低温环境下的变形特征及其诱导的晶体结构和电子结构的变化，以期对实验现象进行准确分析。

为此，本研究将借助分子动力学模拟方法研究 Nb3Sn单晶在极低温环境、高压载荷下的晶体结构变化，此外，还将建立高压下 Nb3Sn单晶超导相转变的解析模型，定量给出应变诱导费米面上电子态密度 变化在高压作用下 Nb3Sn单晶超导相转变中的作用。

1 高压下Nb3Sn 单晶体的分子动力学模拟

利用L A M M P S 程序进行静水压作用下Nb3Sn单晶体的分子动力学模拟，计算模型如图1所示。在LAMMPS 内利用自定义构建晶格的命令建立 Nb3Sn单晶体的A15 立方结构，晶格常数a 为5.29 Å，模拟盒子为边长50a 的正方体，原子数为1 06。 Nb3Sn单晶体的[001]、[010]、[100]晶轴分别对应模拟盒子的x、y、z 3 个方向。为了使模拟结果更接近正常大小的晶体，模拟采用周期性边界条件。利用高斯分布随机给出指定温度下原子的初始速度。

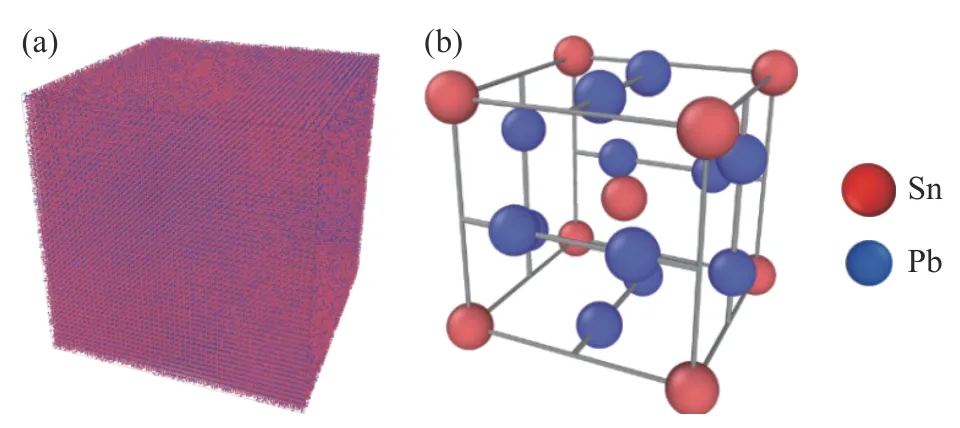
图1 N b3Sn单晶体计算模型（a）和A15 型晶格结构（b）Fig. 1 Calculation model of N b3Sn single crystal (a)and A15 type lattice structure (b)

采用组合势函数的方法定义 N b3Sn原子间的相互作用，Nb-Nb 的势函数采用Zhang 等[21]开发的用于 Ni62Nb38的原子嵌入势，Sn-Sn 的势函数采用MEAM 势函数[22]，Nb-Sn 间的势函数为L-J 势，参数参考文献[23]。计算 N b3Sn单晶体的弹性常数和晶格常数，如表1 所示，其中C 为弹性系数。通过与实验结果和第一性原理模拟[24-26]的比较，证明了该势函数对于力学性能参数表征的可靠性。

表1 Nb3Sn 单晶的力学性能参数Table 1 Elastic constants and lattice constant of Nb3Sn single crystal

加载静水压之前，在4.2～44.2 K 温度区间内均匀取41 个温度点，分别在这些温度点且无外部压强加载条件下用NPT 系综弛豫40 000 步(时间步长为0.001 ps)，使晶体结构达到平衡。弛豫完成之后，对模型连续施加0～10 GPa 的静水压，采用OVITO 软件进行模拟结果的后处理。

2 Nb3Sn 单晶超导转变随压力和温度的演化关系

研究高压下Nb3Sn 超导相的转变行为，除了需要刻画高压下Nb3Sn 单晶体的变形外，还需要对超导转变温度附近的电阻率变化行为进行定量描述。Wiesmann 等[27]建立了一个类似并联电阻形式的N b3Sn 超导材料常态电阻率模型

式中： ρideal为 理想常态电阻率， ρm为饱和电阻率。受此启发，假定超导相转变的电阻率由正常态电阻率ρn和超导态电阻率 ρs相互竞争决定，其中 ρs起到“分流” ρn的作用，基于Yang 等[28]的并联电阻率模型，N b3Sn 单晶超导相转变的电阻率

式 中： Π =ρn/ρs， 为无量纲电阻率函数； ε为压力作用下的应变张量。

2.1 压力-温度耦合作用下的常态电阻率ρn(ε,T)

Nb3Sn超导体在低于临界温度Tc（约40 K）范围内，常态电阻率与温度的关系可表示为[29-30]

式中： ρ0为不依赖于力学变形的残余电阻率；A 为平方项系数，即正常态电阻率的T2依赖关系系数。实验揭示了A15 型超导体常态电阻率的T2依赖性是一种内在性质。不论是电子-电子散射，还是具有非德拜相似声子结构的声子-电子带间散射，都不能完美地解释这种性质[30]。在高压作用下，正常态电阻率的变化依然遵循这一规律。然而，不同的是，压强（应变）会导致系数A 发生变化，所以该关系式可以拓 展为

式 中： Aε为与应变相关的平方项系数，与态密度的平方成正比，所以这里 Aε可以表示为

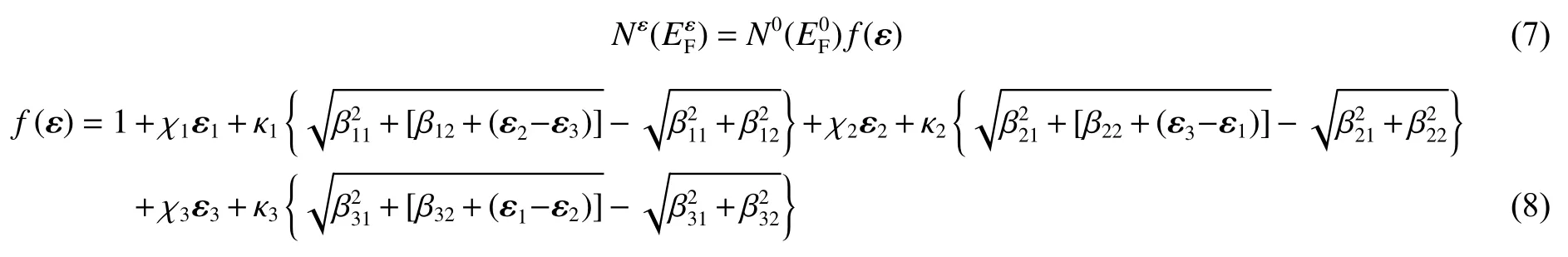
式 中： χi、κi和 βij均为根据第一性原理计算结果拟合得到的参数。将式(7)代入式(6)得到

2.2 无量纲电阻率函数Π

在高压-低温联合作用下，当 Nb3Sn从超导态向正常态转变时，伴随着超导相消失，材料的电阻率逐渐增加。根据电阻率-温度转变曲线变化趋势可以看出，中点转变温度 T1/2(ε)和 无量纲电阻率函数 Π具有两个特点[28]：（1）材料从正常态向超导态转变的过程中，即无量纲温度 TN=T/T1/2(ε)从1 减小到零的过程中， Π将从1 增加到无穷大；（2）当 TN从1 开始增加时， Π从1 到零的转变过程是在1/2 转变温度范围内逐渐完成的。在超导相转变的区间内，电阻率函数（两种极限情形下的电阻率比值）连续变化。基于 Kim 等[32]和Godeke 等[33]的工作，借助修正的Arrhenius 关系给出无量纲电阻率函数的表达式

式中：无量纲参数 κ ≡ΔTW(ε)/T1/2(ε) 描 述了应变作用下超导转变区域的温度宽度， Δ TW(ε)表 示 N b3Sn 单晶超导转变过程中完成电阻率跃变所经历温度区间的宽度。

为了确定电阻率函数 Π的形式，需要确定压力载荷下超导临界温度 T1/2(ε)和 无量纲参数 κ的表达形

式。其中，压力诱导的临界温度变化由Maki De Gennes(MDG)关系式[34]结合临界磁场对温度的偏导数在临界温度处的取值导出

s(ε)为临界温度退化的标定函数，可以表示为

超导转变宽度 ΔTW是 描述电阻率转变的另一个重要参数， ΔTW=T90%－T10%， T90%、T10%分别是电阻率跃变90%和10%对应的温度[35]。基于多物理场环境下 Nb3Sn超导临界曲面表达式的构造方式，通过对 临界温度和临界磁场修正引入应变，根据量纲分析结果和分离变量方法可以给出超导转变宽度[28]

式中：K 为无量纲比例常数， g (H,H1/2(0,ε)) 为关于磁场和上临界磁场的无量纲函数。 N b3Sn单晶在一般加载模式下的上临界磁场可以采用 H1/2(ε)=H1/2(0)s(ε)描述。借鉴Josephson 等[32]和Tinkham 等[35]关于 高温超导体电阻率转变的研究，得出转变宽度和磁场有关，即

进而得出无量纲函数 g 与 s(ε)α(1－h)α成比例。通过上述分析可以得出无磁场作用下无量纲参数 κ在一般加 载模式下的形式

3 结果分析

3.1 高压下晶体结构的变化

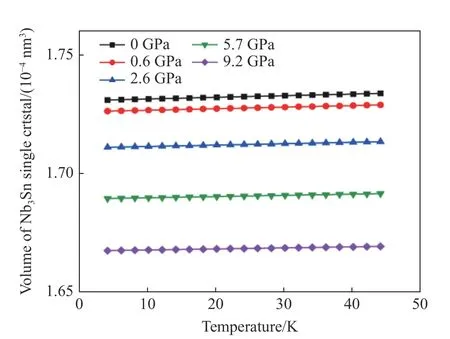
图2 N b3Sn单晶体积随温度的变化Fig. 2 Volume of N b3Sn single crystal varies with temperature

分子动力学模拟可以给出压力和低温环境下Nb3Sn单晶原子尺度的变形和晶格结构变化，对这些细节的分析可以弥补实验观测的不足。图2 给出了4.2～44.0 K 温度区间内模拟单元的体积变化。在无静水压作用（0 GPa）时，随着温度的增加，Nb3Sn单晶体的体积增大。当环境温度从4.2 K 增加到44.0 K 时，体积增大了0.161%。加载0.2、2.6、5.7 和9.2 GPa 静水压时，随着环境温度从4.2 K 增加到44.0 K 时，模拟单元体积分别增大了0.151%、0.138%、0.121%和0.106%，体积变化率依赖于单晶所承受的静水压力载荷。

在4.2 K 低温环境下，当加载的静水压力从0 GPa 提高到10 GPa 时，Nb3Sn 单晶体3 个方向的主应变和体积变化分别如图3(a)和图3(b)所示。图3(a)显示了该静水压加载下的3 个主应变，可以看出3 个主应变均随着静水压的增大而增大，且近似为线性关系。3 个主应变重合，这与经典弹性力学理论吻合，即 ε1=ε2=ε3。随着加载压力增大，到达高压区时与弹性力学分析得到的线性结果不同，主应变与静水压强之间呈弱非线性关系，这起源于高压下原子间的非谐相互作用。一般来说，在弹性阶段加载应力和变形的关系可以用弹性常数描述，弹性常数 Cij为 单位体积内原子间作用总势能 U对应变分量 的二阶偏导数，即

式中： V0为 模拟体系的体积，U 为模拟体系的势能， εi和 εj为应变分量。当施加在Nb3Sn 单晶的静水压强较小时，原子偏离平衡状态的位移较小，考虑势能中原子间相对位移（应变）的二次方项即可准确描述体系的变形，根据式（16）得到弹性模量为常数，即加载应力和变形之间呈线性关系。在高压区，原子偏离平衡状态的位移增大，势能中的原子间相对位移（应变）的高次项（非谐项）不能忽略，从而使得加载应力与变形之间呈非线性变化趋势。由图3(b)可见，单晶体体积随静水压强的增大而减小，静水压达到10 GPa 时， Nb3Sn单晶体体积减小了约4%。

图3 4.2 K 时Nb3Sn 单晶体在静水压作用下的变形情况Fig. 3 Deformation of Nb3Sn single crystal under hydrostatic pressure at 4.2 K

如图4 所示，借助于可视化软件OVITO，对静水压加载下Nb3Sn 单晶体的变形进行可视化处理，给出了 Nb3Sn单晶体静水压加载下平面的平均应力和整体及局部原子的Mises 应力分布。图4(a)给出了Nb3Sn 单晶体平面的平均应力 σxx、 σyy和 σzz，可以看出平均应力在10 GPa 左右。图4(b)为 Nb3Sn单晶体的Mises 应力分布云图，可以看出：在10 GPa 静水压作用下， Nb3Sn单晶体发生了明显的晶格畸变；但晶体结构完整，没有发生损伤；Mises 应力主要集中在Nb 原子上。图4(c)为 Nb3Sn单晶体原子等效应力的分布直方图，可以看出应力35 GPa 以上的原子数是2 GPa 左右的3 倍。从应力分布上看，Sn 原子的应力明显小于Nb 原子。模拟结果表明，Sn 原子所受局部Mises 应力接近2 GPa，而Nb 原子的Mises 应力在37 GPa 左右。

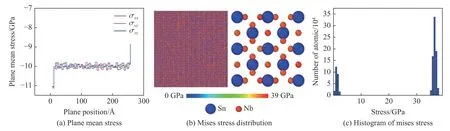
图4 静水压加载下N b3Sn单晶体的应力分布Fig. 4 Stress distribution of N b3Sn single crystal under hydrostatic pressure

图5 给出了 Nb3Sn 单晶体主应力在xz 面上整体及局部原子的主应力云图，其中 σ1、 σ2和 σ3分别为沿着x、y 和z 方向的主应力。可以看出，各方向Sn 原子均受到较大的压应力，且该压应力大于Nb 原子受到的应力，约为57 GPa；当Nb 原子所在Nb 链的方向与主应力方向平行时，会受到一个压应力，而其他方向Nb 链原子在该方向的应力表现为拉应力，但图5 显示所有Nb 链原子所受的应力大小大致相同，均在20 GPa 左右。在静水压作用下，Sn 原子承受的主应力在各方向均为压应力，Nb 原子在所在Nb 链方向承受的主应力为压应力，其他方向承受的主应力为拉应力，这也是导致等效应力主要集中在Nb 链原子的原因。

图5 N b3Sn 单晶体xz 面的主应力分布Fig. 5 Principal stresses distribution of N b3Sn single crystal on the right side under hydrostatic pressure

3.2 高压下的超导相变

为了研究 N b3Sn 超导材料的压力敏感性，Ren 等[16]通过实验研究了高压下 N b3Sn 单晶体的电阻转变行为。基于上述高压下Nb3Sn 单晶体的变形分析，借助本研究所建立的超导相转变模型，对实验给出的经验关系进行解释。模型参数C 和通过 Ren 等[16]的实验结果进行最优化拟合，其他参数由实验结果直接给出，如表2 所示。计算中的态密度模型参数来源于第一性原理模拟结果[31]，如表3 所示。

表2 电阻率模型相关参数Table 2 Parameters of resistivity model

表3 态密度函数相关参数Table 3 Parameters of density of state function

图6 中实线部分给出了0～44 K 温度范围内 Nb3Sn单晶体在静水压作用下的电阻率预测值。可以看出，常态电阻率部分与实验数值[16]基本吻合，所建立的计算模型能够准确刻画出实验观测到的超导转变温度附近电阻率的T2依赖性。对于常态电阻率部分，其斜率随着静水压的增加而减小。在超导转变区域，临界温度随着静水压的增大而减小，由于分子动力学模拟中选取的温度间隔较大，超导转变过程不够平缓，并没有完整的呈现，但是仍然可以看出随着静水压强增大，超导转变过程逐渐向后推移，与实验数据定性吻合。

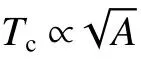
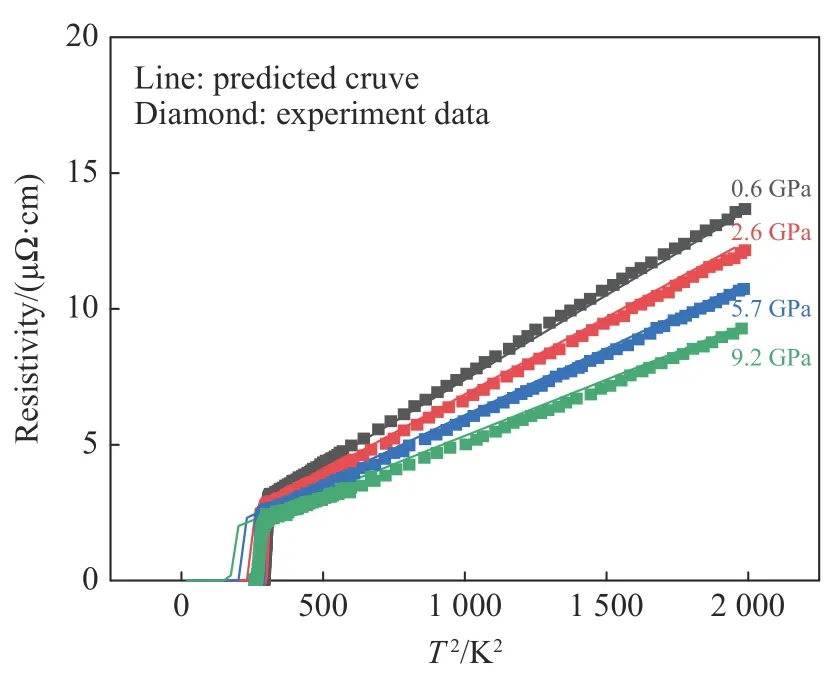
图6 静水压作用下Nb3Sn 单晶体在低温区的电阻率随温度的变化Fig. 6 Change of resistivity with temperature in low temperature area for Nb3Sn single crystal under hydrostatic pressure

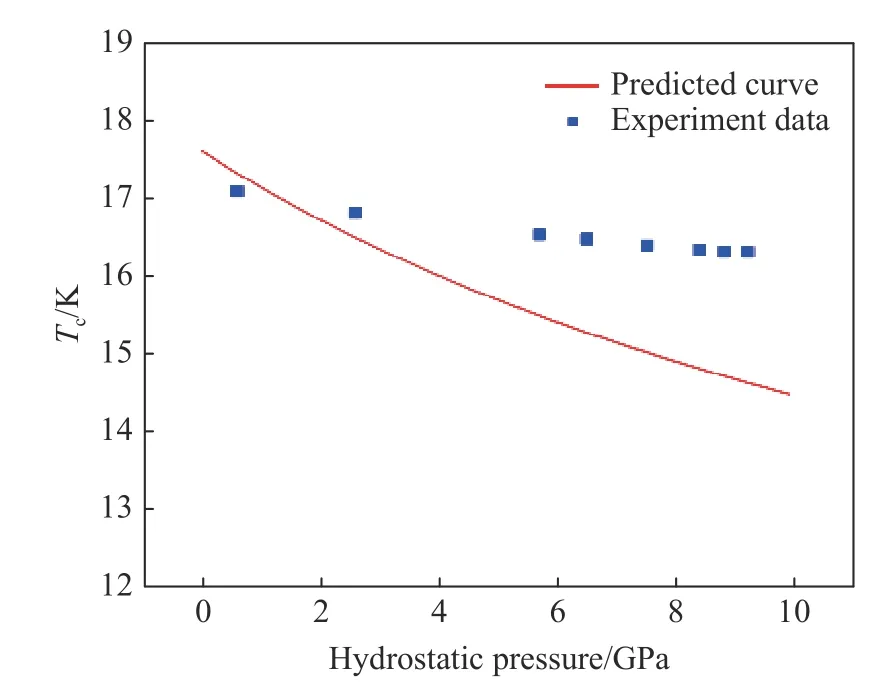
图7 静水压作用下Nb3Sn 单晶体临界温度变化预测结果与实验结果对比Fig. 7 Comparison between the predicted and measured critical temperature of Nb3Sn single crystal under hydrostatic pressure

4 结 论

基于分子动力学模拟方法研究了高压下 Nb3Sn单晶体的晶体结构和局部原子应力，在此基础上，受Wiesmann 并联电阻率模型的启发，基于 Nb3Sn单晶体常态电阻率的T2依赖性，建立了高压下Nb3Sn 单晶体的超导相转变模型。结果表明：高静水压作用下 Nb3Sn单晶体发生了明显的晶格畸变，但晶体结构完整，没有发生损伤；高静水压作用下电阻率转变的模型预测结果与实验观测结果吻合较好，证明了压力诱导费米面上电子态密度的变化在高压下 Nb3Sn单晶体超导相转变中的作用。相关研究结果对于理解高压下 Nb3Sn 单晶体的超导相变行为具有重要意义，同时为后续研究高压下 Nb3Sn多晶体以及复合多晶体的相变行为奠定了基础。