基于特征优选和HHO-SVM 的变压器故障识别

朱楚昱，李 川，李英娜

（昆明理工大学 信息工程与自动化学院，云南 昆明 650500）

0 引 言

变压器故障识别方法中，分析油中溶解气体特征关系是提高故障诊断的关键，其中三比值法最具代表性。但是，三比值编码并不完全，且三比值的边界过于绝对，对故障的特征信息有所遗漏［1-7］。变压器运行中出现故障时，变压器油中的各种反应机理复杂，且不同故障情况下油中产生的不同气体间的关联特征存在差异［8-12］。近年来，分析气体更多的特征的研究有了一些积累。2012 年，中南大学信息科学与工程学院唐勇波利用主成分分析计算样本各变量的重构贡献率作为特征量，且经过实例验证了该特征量能够体现一部分故障信息［8］。2017年，西南交通大学吴广宁从增加新的数据量入手，将相关的电气试验等数据加入到油中溶解气体分析［9］。2018 年，国网山东省电力公司电力科学研究院辜超选取气体间的16 种比值作为特征量，计算出最优的9 种比值组合［10］。2019 年，中国石油大学梁永亮采用不同故障状态下气体间较稳定的MIC 的关联度值作为特征量，通过最大信息系数方法（Maximal Information Coefficient，MIC）计算每两对气体间的关联程度［11］。2020 年，宜春学院江风云通过对输入样本在相空间上重构，然后用KECA 对重构相空间提取核熵成分作为输入［12］。

然而，在对DGA 数据特征进行提取方面，目前以全故障类型的特征分析为主，引入新的比值或是相空间重构，而没有考虑到不同故障类型下气体体现的故障特征的差异性，可能会造成包含故障的特征信息被忽略。因此，本文依据样本故障信息，结合特征气体数据和三比值，将数据集划分为6 种不同故障类型的子集，并针对每一种故障类型子集，利用核主元分析模型提取该故障类型下的主元特征。

在智能技术应用现状下，利用模糊聚类、神经网络以及支持向量机等算法的变压器故障诊断模型降低了故障的误判，但这些机器学习算法在学习迭代上各自存在欠缺。例如，局部最优解是神经网络经常遇到的问题，模糊聚类学习能力不足。相比之下，SVM 能在高维度、小样本量以及非线性的数据集上具有良好的分类能力。利用哈里斯鹰搜索算法优化SVM 参数，可进一步提高SVM 的泛化能力和鲁棒性［13-15］。

综上所述，本文根据实际故障类型将样本划分成6 个单一的故障数据子集，采用KPCA 算法提取各个单一数据集上的故障特征，采用HHO 算法优化SVM 参数，从而对DGA 样本进行故障识别。

1 基于核主元分析的故障特征提取

1.1 油中溶解气体特征量

本文统计了历年来相关技术刊物上公布的变压器油中溶解气体分析的气体数据，选出实际变压器运行故障类型明确的数据1 013 条，剔除明显异常的数据样本，如气体含量值为负数、样本数据不完整等，最后得到共932 组可用的样本数据集。

改良三比值的特征反映了主要的部分变压器故障信息，但气体含量也含有表征故障的信息［1］。除了考虑三比值，本文还选取气体含量作为特征补充。具体地，将H2的气体含量值转换为H2占氢烃总气体含量值的比值，将其他4 种气体的含量值转换为其各自占总烃含量的比值［16］，如表1 所示。

表1 油中溶解气体特征量

1.2 基于KPCA 的故障特征提取

通过引入核主元分析（Kernel Principal Component Analysis，KPCA）方法，对气体间的非线性关系进行处理。将样本数据集Xm×n（X∈RD）映射到高维空间，从而在高维特征空间H上计算不同故障类型的关联特征。大体思想是引入非线性映射函数φ，在H中对映射的数据φ(x)的协方差矩阵进行特征值分解［8］。

本文依据样本故障信息，将选取的DGA 和三比值数值结合的数据集划分为7 种不同故障类型的子集，分别是局放故障、低能火花、高能电弧、低温度过热、中温度过热和高温度过热6 种故障类型。采用高斯核主元分析，针对每一种故障类型子集，提取该故障类型的主元特征。

根据累计贡献率大于85%来确认每种故障类型的主元个数。各故障类型的核主元个数及累计贡献率结果，如表2 所示。经KPCA 分别提取各故障4 个主元特征量，总故障特征量共24 个。

表2 各故障类型核主元个数

2 基于HHO-SVM 的变压器故障识别

2.1 支持向量机（SVM）原理

支持向量机（Support Vector Machine，SVM）算法是由Vladimie 等提出的一种监督学习方法，利用统计学习理论和结构风险最小化原理对数据进行分类，原理如图1 所示。它的中心思想是通过迭代求出尽可能使所有样本距离该最优超平面最大的最优超平面［17-19］。

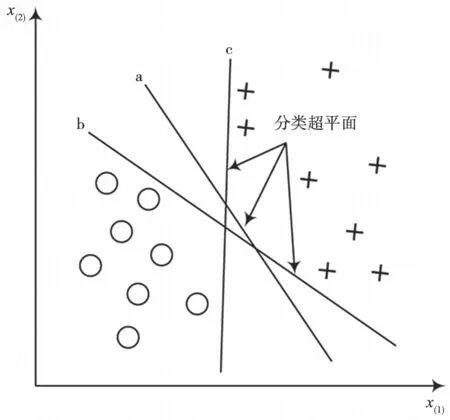
图1 支持向量机原理示意图

超平面可用式（10）表示，将最优分类面问题转换成二次规划优化问题：

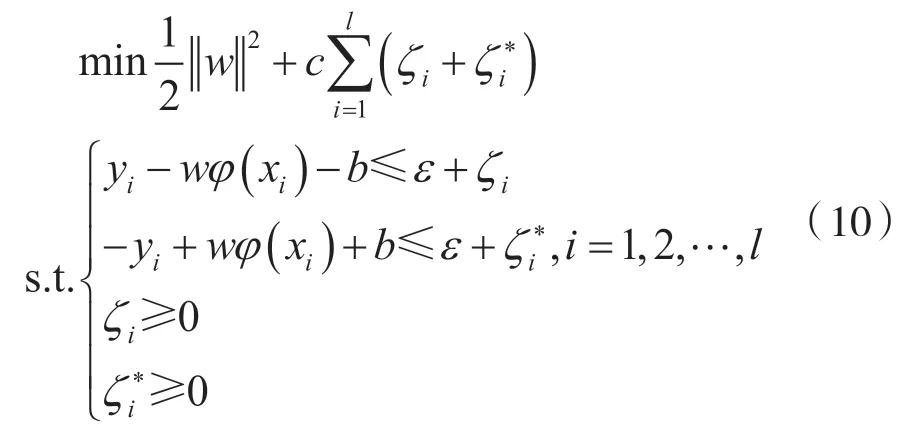
式中，c为惩罚参数；ζi和ζi*为松弛变量；ε为不敏感参数。

经过非线性映射后的空间内构造的分类器模型为：

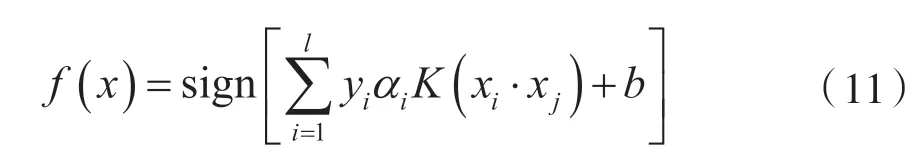
式中，αi为拉格朗日系数。

2.2 哈里斯鹰搜索（HHO）算法原理

哈里斯鹰搜索算法是（Harris Hawks Optimization，HHO）是2019 年Heidar 等提出的一种元启发式搜索算法。搜索过程主要分为探索阶段、探索与开发转换阶段和开发阶段［19-21］。

2.2.1 搜索阶段

哈里斯鹰的初始位置由两种策略决定。

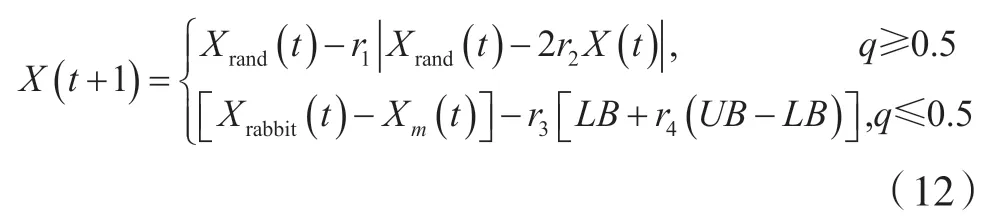
式中，X(t+1)是下一次迭代过程中鹰的位置向量；t为迭代次数；Xrand(t)当前种群中随机选择的鹰的位置；Xrabbit(t)为猎物的位置，即最优适应度的个体位置；r1、r2、r3、r4和q都是［0，1］之间的随机数，q用于随机选择要采用的策略；LB、UB是变量的下限和上限；Xm(t)为个体平均位置，表达式为：

式中，Xi(t)为种群中第i个个体的位置；N表示种群规模。

2.2.2 搜索与开发转换阶段

根据猎物逃逸能量的取值，鹰群选择开发阶段将开展的行为，并在不同的行为之间进行转换。猎物的逃逸能量E为：

式中，T是最大迭代次数；E0是E的初始值，为（-1，1）内的随机数。当|E|≥1 时，鹰群通过遍历不同的区域寻找猎物的位置，即执行探索阶段；当|E|＜1，算法开始求解在探索阶段时的解的邻域，即开发阶段。

2.2.3 开发阶段

此阶段中，根据猎物的逃逸行为和哈里斯鹰的追逐策略，提出了软围攻策略、硬围攻策略、渐进式快速俯冲的软包围策略以及渐近式快速俯冲硬包围策略4 种可能的策略来模拟攻击阶段。

（1）软围攻策略

当0.5 ≤|E|＜1 且r≥0.5 时，采取软围攻更新位置：

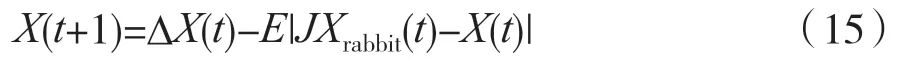
式中，∆X(t+1)=Xrabbit(t)-X(t)表示猎物位置与个体当前位置的差值；∆X(t)为最优个体和当前个体的差值；r5为0 到1 内的随机数；J为猎物逃跑过程中的跳跃距离，为［0，2］之间的随机数，如：

（2）硬围攻策略

当|E|＜0.5 且r≥0.5 时，采取硬围攻更新位置：

式中，相关变量的物理意义同上，不再赘述。

（3）渐进式快速俯冲的软包围策略

当0.5 ≤|E|＜1 且r＜0.5 时，采取渐近式快速俯冲的软包围更新位置。进攻前，哈里斯鹰通过以下两个策略形成软包围圈。当策略一无效时，执行策略二。

第一个策略更新式为：

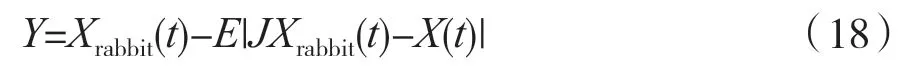
第二个策略更新式为：

式中，D为问题维度；S是一个D维随机向量，其中元素为［0，1］之间的随机数；LF(·)是莱维（Levy）飞行函数，如：

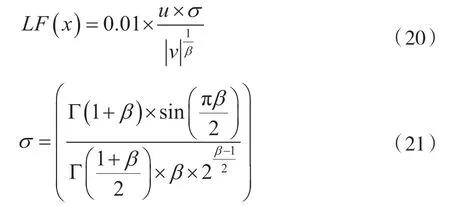
式中，l、m为［0，1］内的均匀分布的随机数，β为1.5 的常数。因此，该阶段更新策略最终为：

（4）渐近式快速俯冲硬包围策略

当|E|＜0.5 且r＜0.5 时，采取渐近式快速俯冲的硬包围更新位置。在突袭前，哈里斯鹰采用以下策略进行狩猎，形成一个硬包围圈。

如图2 所示，建立变压器故障识别模型时，首先对KPCA 提取特征的特征量划分训练集并采用支持向量机进行训练，其中核函数选择径向基函数。其次，利用哈里斯鹰搜索算法求解全局最优的惩罚参数c和核参数g，以模型训练过程的分类准确率作为适应度函数。最后，通过测试集对模型进行验证。

图2 HHO-SVM 算法流程图

3 实例与结果分析

3.1 实例验证

将收集到的934 组变压器故障数据经KPCA 处理提取24 个特征，并将其作为输入。针对电力变压器故障识别最常见的有6 种故障状态，即局放故障、低能火花、高能电弧、低温度过热、中温度过热和高温度过热共6 种故障状态作为相应的输出。表3 为932 组变压器故障样本分类。

在HHO-SVM 故障识别模型中，初始化算法各项参数：种群规模50，莱维飞行函数参数1.5，迭代次数50，优化的参数范围［0.01，10］，训练集的分割比为0.8。

采用HHO-SVM 模型进行变压器故障识别，使用哈里斯鹰对SVM 的惩罚参数c和核函数参数g进行优化时，随着迭代次数的增加，参数序列的最佳适应度曲线和平均最佳适应度曲线如图3 所示。此时，求出的最优惩罚参数c的解为4.573，核函数参数g的解为0.186。

分别将最优惩罚参数和核函数参数的解带入SVM，将故障特征量样本作为输入，最终得到的支持向量机的训练集故障识别准确率为93.42%，测试集故障识别的准确率为94.17%。测试集结果与实际对比，如图4 所示。

表3 932 组变压器故障样本分类

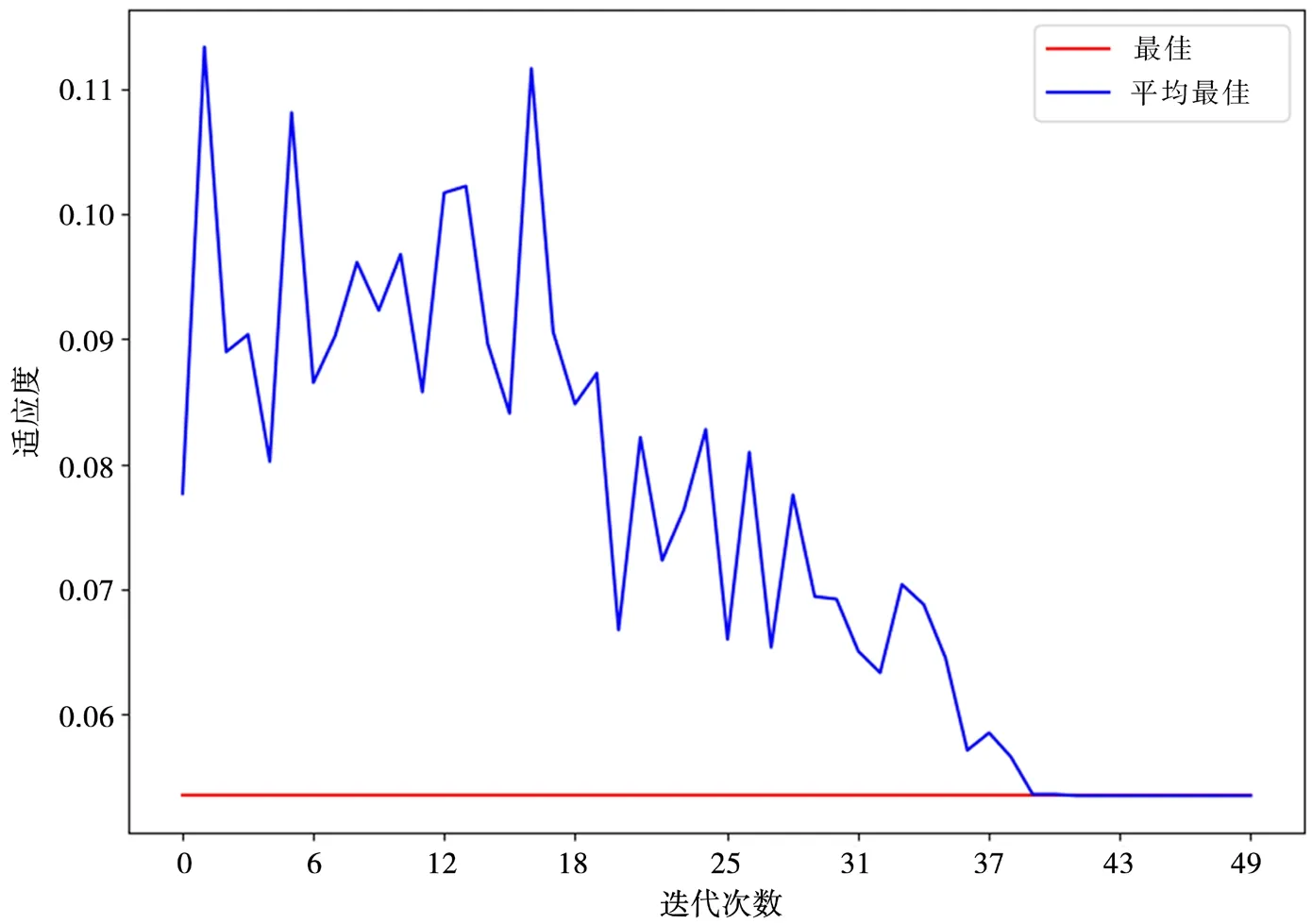
图3 HHO 最优适应度曲线

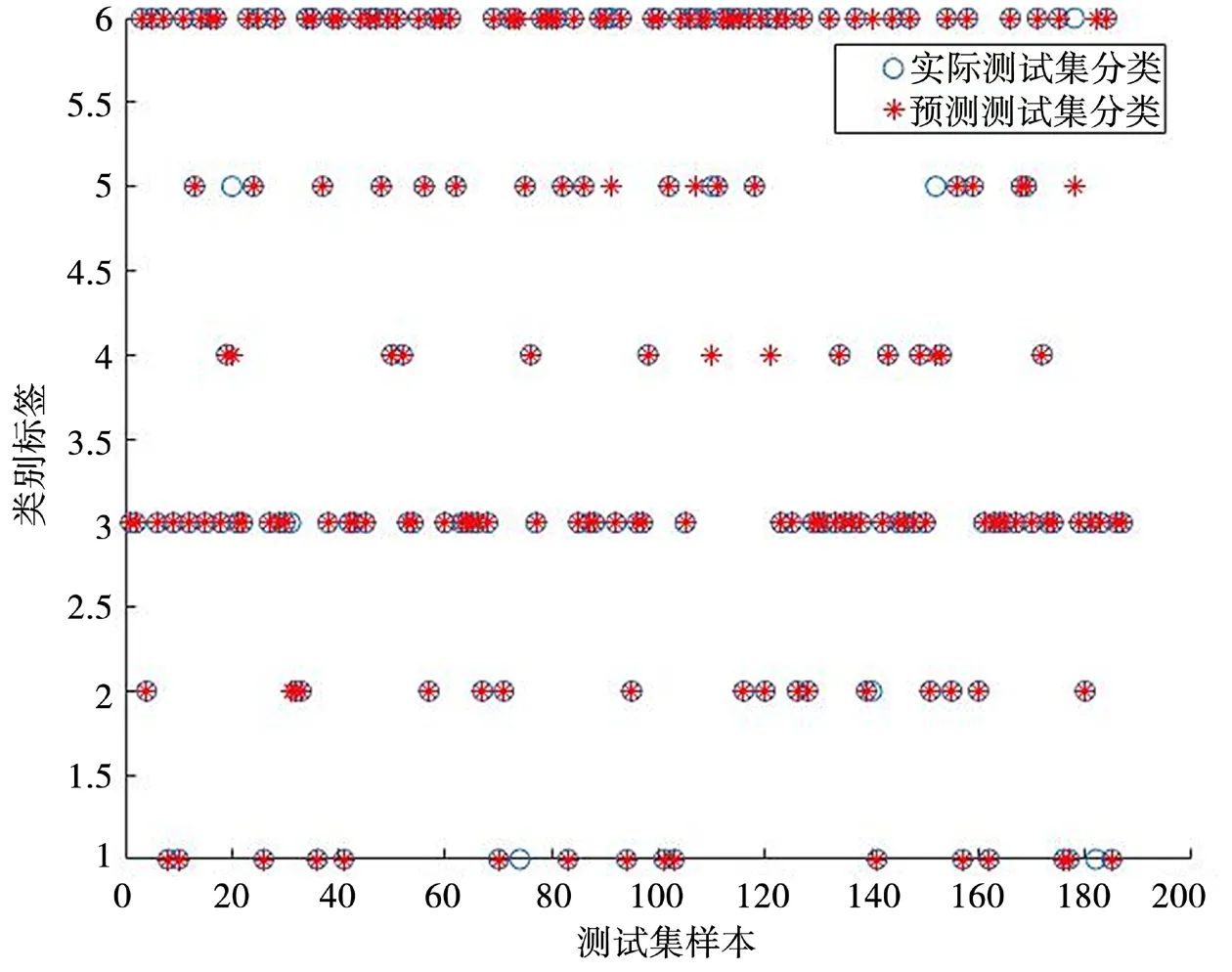
图4 测试集分类结果与实际结果对比

利用HHO-SVM 模型训练样本数据，建立电力变压器故障诊断模型。结果表明，测试集分类准确率为94.17%。测试集各故障子集分类结果如表4所示。

3.2 诊断方法对比

为了进一步验证HHO-SVM 故障识别模型的有效性，分别以不同方法对变压器故障诊断的正确率进行比较，如表5 所示。单一特征组合的故障识别正确率分别为55.16%和56.15%，三比值的正确率要高于气体含量比值。而混合特征组合的正确率比单一特征组合分别高14.36%、13.37%，说明将DGA 数据和三比值组合后包含的故障信息比单一特征组合多。同时，就DGA 数据结合三比值提取故障特征来说，KPCA 提取特征的正确率高出24.65%，明显提高了变压器故障诊断正确率，体现出各故障特征之间存在一定的差异。

表4 HHO-SVM 模型测试集正确率

表5 不同特征量的平均正确率

基于相同的特征组合，采用标准SVM、PSOSVM 和HHO-SVM 分别进行变压器故障诊断的故障识别。如表6 所示，与PSO-SVM 相比，HHOSVM 的平均测试准确率高出5.72%，说明HHOSVM 算法体现出较好的局部和全局优化性能，可以提高变压器故障诊断准确率。

表6 不同方法的平均正确率

4 结 论

在DGA 数据集的基础上加上三比值数集，并划分为6 种不同故障类型的子集，分别对每一种故障类型子集利用KPCA 提取该故障类型的主元特征，再建立HHO-SVM 变压器故障识别模型进行故障识别，可获得如下结论。

（1）利用KPCA 依次提取各故障类型子集特征的方法，正确率比不采用KPCA 的测试正确率分别高出39.01%、38.02%，可见所提出的DGA 数据包含三比值特征缺失的故障信息，因此DGA 数据结合三比值能更准确反映变压器的故障。同时，就DGA 数据结合三比值提取故障特征来说，KPCA 提取特征的正确率高出24.65%，明显提高了变压器故障诊断正确率，体现出各故障特征之间存在一定的差异。

（2）建立了基于哈里斯鹰搜索算法优化的SVM故障识别模型，与SVM、PSO-SVM 模型相比，测试集分类准确率有一定的提高。

（3）以KPCA 分别提取的各故障组合为输入的HHO-SVM 变压器故障诊断模型平均正确率高达94.17%，验证了所提方法的有效性。