改进的基于奇异值分解的抗差容积卡尔曼滤波算法在全球定位导航中的应用
王姚宇, 陈仁文*, 张 祥
(1.南京航空航天大学机械结构力学及控制国家重点实验室, 南京 210016; 2.东南大学信息科学与工程学院, 南京 211102)
非线性动态系统的非线性和噪声不确定问题,导致传统卡尔曼滤波不适用于非线性模型的状态估计[1-2]。扩展卡尔曼滤波(extended Kalman filter,EKF)虽然可用于非线性系统滤波[3-5],但是其线性化环节会引入高阶截断误差,且Jacobi矩阵的计算会增加运算的难度,在实际工程应用中效果不佳。无迹卡尔曼滤波(unscented Kalman filter,UKF)克服了EKF的局限性[6-10],UKF基于(unscented transformation,UT)变换构建了一系列Sigma点,以此逼近状态向量的后验概率密度函数,实现简单且精度远远高于EKF,但是在状态发生突变的情况下,UKF的鲁棒性不佳,精度容易受到影响。容积卡尔曼滤波(cubature Kalman filter,CKF)利用三阶球面径向容积准则对概率密度函数进行近似[11-14],其采样点的权值均为正数,相较于上述滤波算法,CKF的精度和稳定性都有所提高,为解决非线性估计问题提供了一个新思路。
但是非线性滤波普遍存在跟踪能力弱和自适应能力差的问题,当系统受到异常观测值或者状态突变的影响时,滤波器容易产生精度降低甚至发散的情况。文献[15]提出了均值滤波的思想对采样数据进行了预处理,降低了异常观测值的干扰,增快了系统的响应时间。文献[16-17]中引入了奇异值分解(singular value decomposition,SVD)的办法,减小了先验协方差矩阵负定性变化,保证算法可以平稳地迭代。文献[18]提出一种抗差方法,能够有效减弱波动较大数据对于滤波器稳定性的影响。
在卡尔曼滤波器进行迭代更新时,波动较大的数据采集点会减慢滤波器的收敛速度,影响数据的稳定性。在工程试验中,环境干扰会引入较大的噪声,对量测数据产生影响,严重偏离真实值。为了解决滤波更新状态不稳定和异常观测值影响大的问题,提出一种改进的基于SVD的CKF抗差算法,采用均值滤波的方法,对干扰大的数据、瞬时脉冲信号等进行处理,同时使用抗差方法减弱异常观测值的影响,使滤波器可以更好地运行下去,改善滤波效果,提高滤波器更新迭代的稳定性,对异常观测值有较好的修正效果。计算仿真验证该算法的有效性。
1 算法描述
1.1 均值滤波
均值滤波的思想是先选取一个长度为N的均值滤波窗口,从头开始,以N个采样数据为一组,求取其均值作为一个新的采样点,随后将窗口向后移动一个数据,用新的采样数据替换掉窗口的第1个采样数据,以此类推,获得一组求取均值后的新的采样点,作为滤波器的输入值[19],其基本工作原理如图1所示。
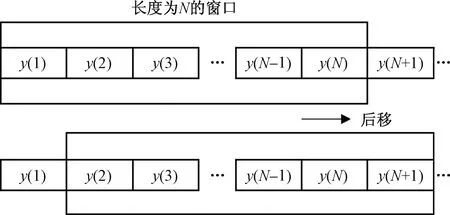
图1 均值滤波基本工作原理Fig.1 Basic working principle of mean filtering
均值滤波的原理用算式可以表示为
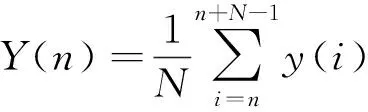
(1)
式(1)中:y(i)为原采样数据;Y(n)为均值滤波后新产生的数据,对于长度为M的数据列而言,n=1,2, 3,…,M-N,N为均值滤波窗口长度。均值滤波窗口的长度可以根据实际采样点数的多少进行调节,合适的窗口大小可以获得更好的滤波效果。
1.2 SVD分解
随着容积卡尔曼滤波器的不断迭代,状态向量和观测向量的协方差阵可能会出现负定的情况,导致滤波器的状态无法准确更新,甚至出现无法收敛的现象。SVD分解也叫奇异值分解,其数值计算具有较强的鲁棒性,用SVD分解代替Cholesky分解,计算容积点协方差矩阵,可以有效增强滤波更新的稳定性。
SVD分解的方法是,对于一个m×n维的实数矩阵A,可以分解为
A=UΛVT
(2)
式(2)中:U、V均为单位正交阵,分别称为左奇异矩阵和右奇异矩阵;Λ仅在主对角线上有值,其余元素均为0,一般形式表示为
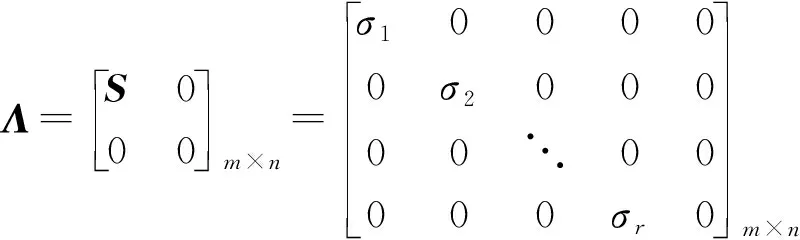
(3)
式(3)中:S=diag(σ1,σ2,…,σr)为奇异值矩阵,且σ1≥σ2≥…≥σr≥0,r为矩阵S的秩。
1.3 抗差方法
观测信息在不断参与更新过程,异常的观测值会严重影响滤波结果,需要引入抗差因子减小异常观测值对CKF滤波过程的干扰[20],当观测信息精度高时,加大观测值在状态估计中的权值;反之,当观测信息误差偏大时,降低观测值在状态估计中的权重。
类似IGGIII等价权函数模型,将观测残差值进行分类,分为3个等级进行筛选,分别对应3种不同的抗差因子,即
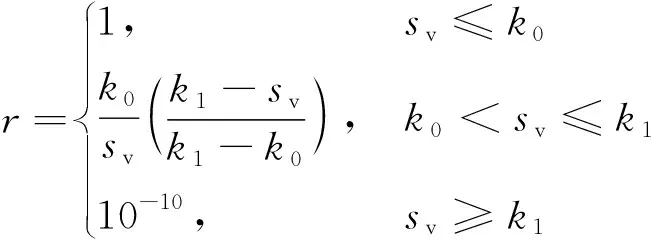
(4)
式(4)中:k0、k1为常值,通常选取k0=1.5~2.0,k1=3.0~8.5;sv为标准化残差[21]。这里要注意的是,抗差因子不能设置为0,否则可能影响观测向量协方差矩阵的迭代更新。
1.4 改进的抗差SVD-CKF算法
考虑一个非线性系统:
xk=f(xk-1)+ωk
(5)
zk=h(xk)+vk
(6)
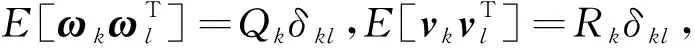
改进的抗差SVD-CKF算法步骤如下。
1.4.1 状态参数初始化
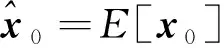
(7)
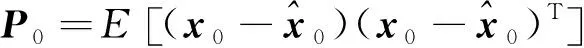
(8)
1.4.2 时间更新过程
使用SVD分解代替传统Cholesky分解,对协方差矩阵Pk-1|k-1进行分解,并计算容积点Xi,k-1|k-1。
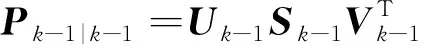
(9)
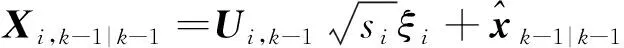
(10)
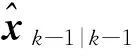
通过状态方程来传播容积点:
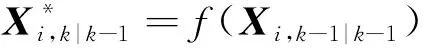
(11)
预测状态值:
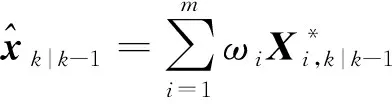
(12)
式中:m为容积点集矩阵的列数,通常为状态维数n的2倍;ωi为容积点相应的权值,平均分配权值为ωi=1/2n。
预测协方差矩阵:
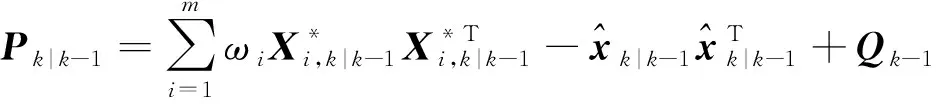
(13)
1.4.3 量测更新过程
对时间更新过程中求得的协方差矩阵进行SVD分解,并计算容积点:
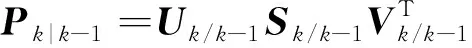
(14)
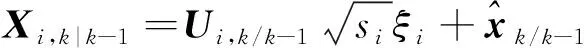
(15)
通过量测方程来传播容积点:
Zi,k|k-1=h(Xi,k|k-1)
(16)
加权求和预测量测值:
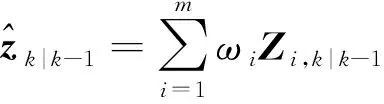
(17)
使用均值滤波后的观测值计算残差值:
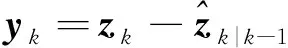
(18)
标准化观测残差值:
svk=yi,k/σi,k
(19)
式(19)中:yi,k为残差向量的第i个分量;σi,k为其标准差。
预测观测协方差矩阵,这里要根据观测残差值引入抗差因子rk,对观测噪声方差阵进行修正,即
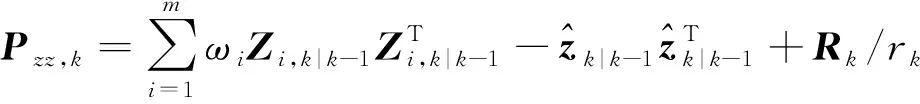
(20)
预测互协方差阵:
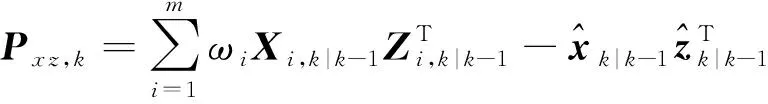
(21)
1.4.4 滤波更新
计算卡尔曼滤波增益:
Kk=Pxz,k/Pzz,k
(22)
利用先验估计值和均值滤波后的观测值进行状态估计更新:
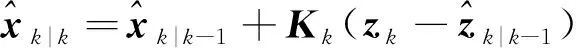
(23)
进行协方差矩阵更新:
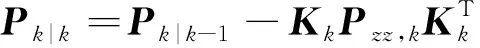
(24)
算法的具体流程如图2所示。
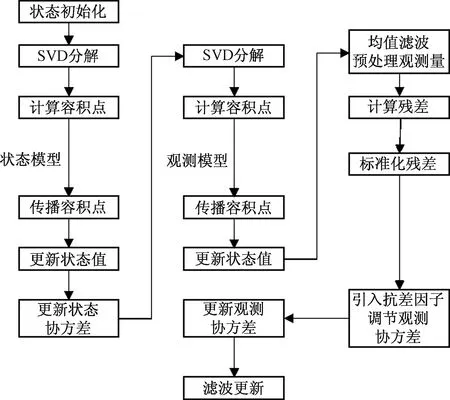
图2 改进的抗差SVD-CKF算法流程Fig.2 Flow chart of improved robust SVD-CKF algorithm
2 运动模型建立
2.1 状态方程
本文的算法应用于基于GPS导航的智能割草机平台,首先需要建立模型来描述其运动状态。由于割草机主要在平面草地上工作,其滚转角和俯仰角可近似为0°,只考虑其在水平平面内的运动状态,其主要运动状态为匀速直线运动,因此以东向位置xe,东向速度ve,北向位置xn,北向速度vn作为状态变量来建立状态方程,k+1时刻的状态可由k时刻的状态得到,可以得到如下的状态方程:
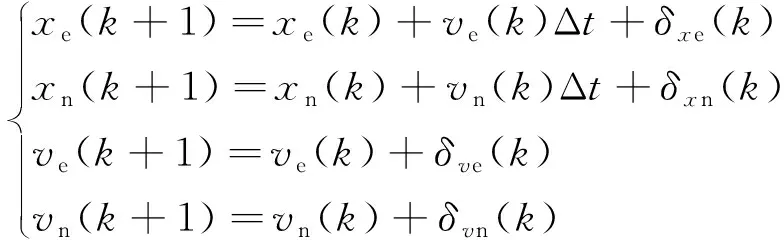
(25)
式(25)中:δ为过程噪声;Δt为采样时间间隔。状态方程反应了不同时刻下状态量之间的相互关系,其可简单地表示为
X(k+1)=FX(k)+Q(k)
(26)
式(26)中:X为状态量;F为状态转移矩阵;Q为系统噪声矩阵。
2.2 量测方程
量测方程是针对GPS导航系统量测过程的模型假设,GPS所获得的量测值有纬度L,经度λ,对地航速v,对地航向α。GPS所测得的原始位置坐标处于地理坐标系,需将其转换到东北天坐标系,在考虑地球偏心率e不是很大的情况下,可以近似用以下公式进行转换,即
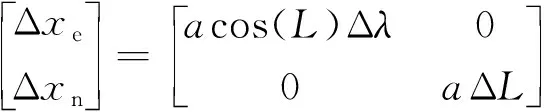
(27)
式(27)中:a为地球的长半径;ΔL为当前位置点与起始点的纬度差;Δλ为当前位置点与起始点的经度差。同时,也需要将GPS所测得的速度转换到东北天坐标系,整合后的量测方程为
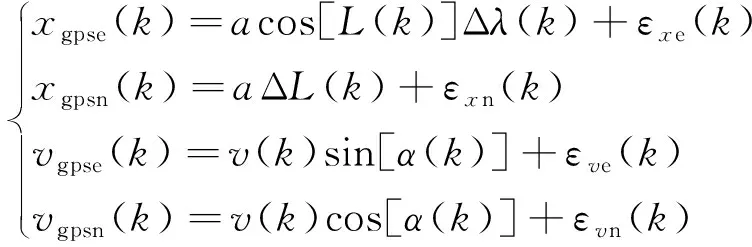
(28)
式(28)中:ε为量测噪声;v为测得的载体对地航速;α为载体坐标y轴与正北方向的夹角,范围为0°~360°。量测方程可简单地表示为
Z(k)=HX(k)+R(k)
(29)
式(29)中:Z为观测量;H为量测矩阵;R为量测噪声矩阵。
3 仿真结果与分析
研究的GPS系统运用于割草机平台,该平台主要进行U字形自主作业,需要保证直线段匀速运动的位置准确性。为了验证算法的可行性,采用MATLAB进行仿真分析。假设GPS平台的采样频率为5 Hz,选取一段采样时长为100 s的匀速直线运动段,其对地航速v=0.15 m/s,对地航向角α=75.7°。以此运动状态为真实值,以东向位置、北向位置、东向速度和北向速度为状态量进行分析,验证算法的有效性。
3.1 抗差SVD-CKF滤波效果分析
由于在状态转移和量测的过程中存在噪声的不确定性,在位置真实值上引入一组均值为0,方差为0.01的高斯白噪声,在速度真实值上引入一组均值为0,方差为4×10-4的高斯白噪声,以此来作为GPS系统采集处理后的观测值。图3和图4所示分别为经过传统CKF滤波后的位置和速度误差,图5和图6所示分别为经过抗差SVD-CKF滤波后的位置和速度误差。可以看出,经过传统CKF滤波后的误差相较于原始误差值波动幅度有所减小,但是波动仍然较为剧烈;经抗差SVD-CKF滤波后的误差值明显平缓,说明其状态估计更具稳定性。
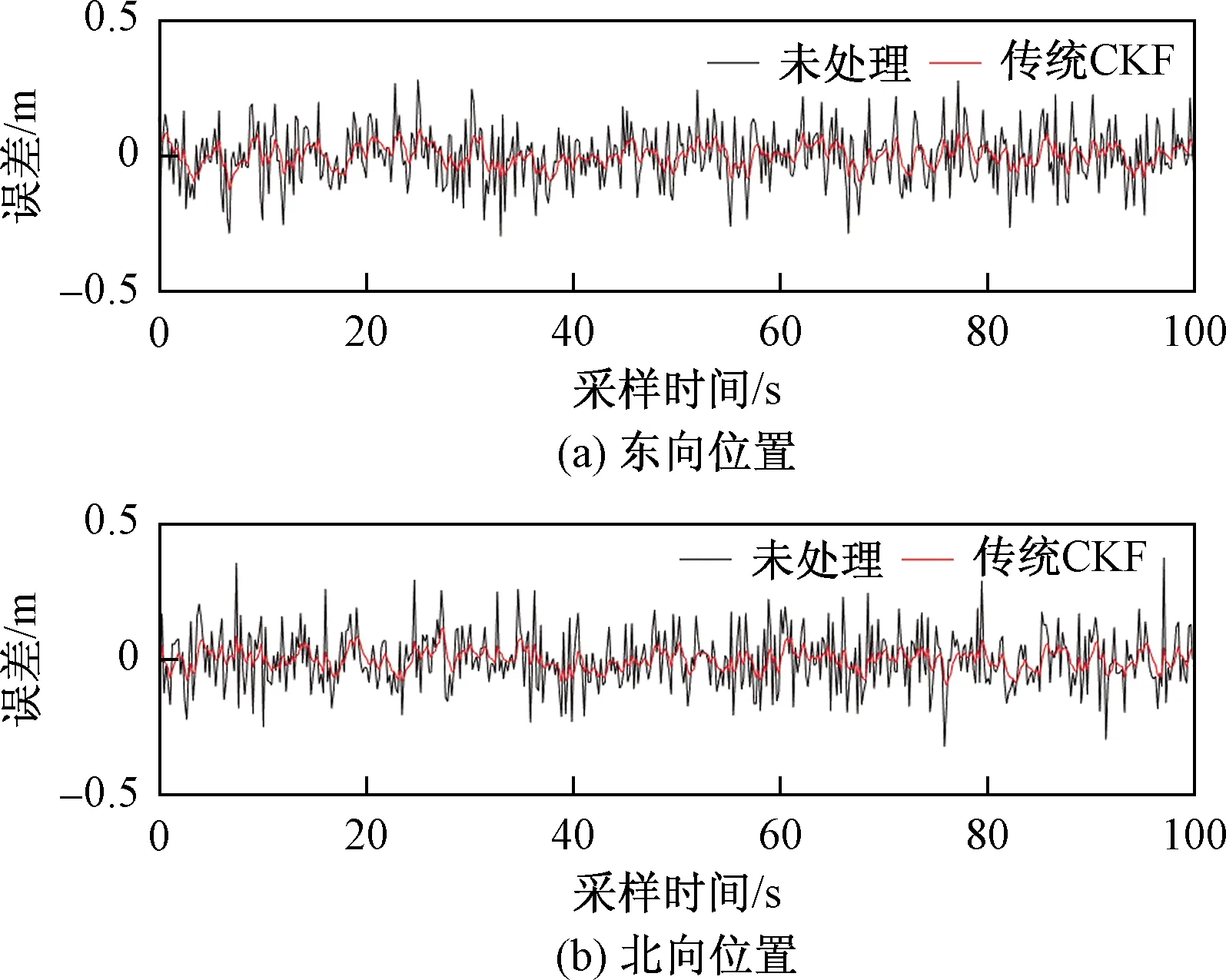
图3 传统CKF滤波后位置误差Fig.3 Position error after traditional CKF filtering

图4 传统CKF滤波后速度误差Fig.4 Velocity error after traditional CKF filtering
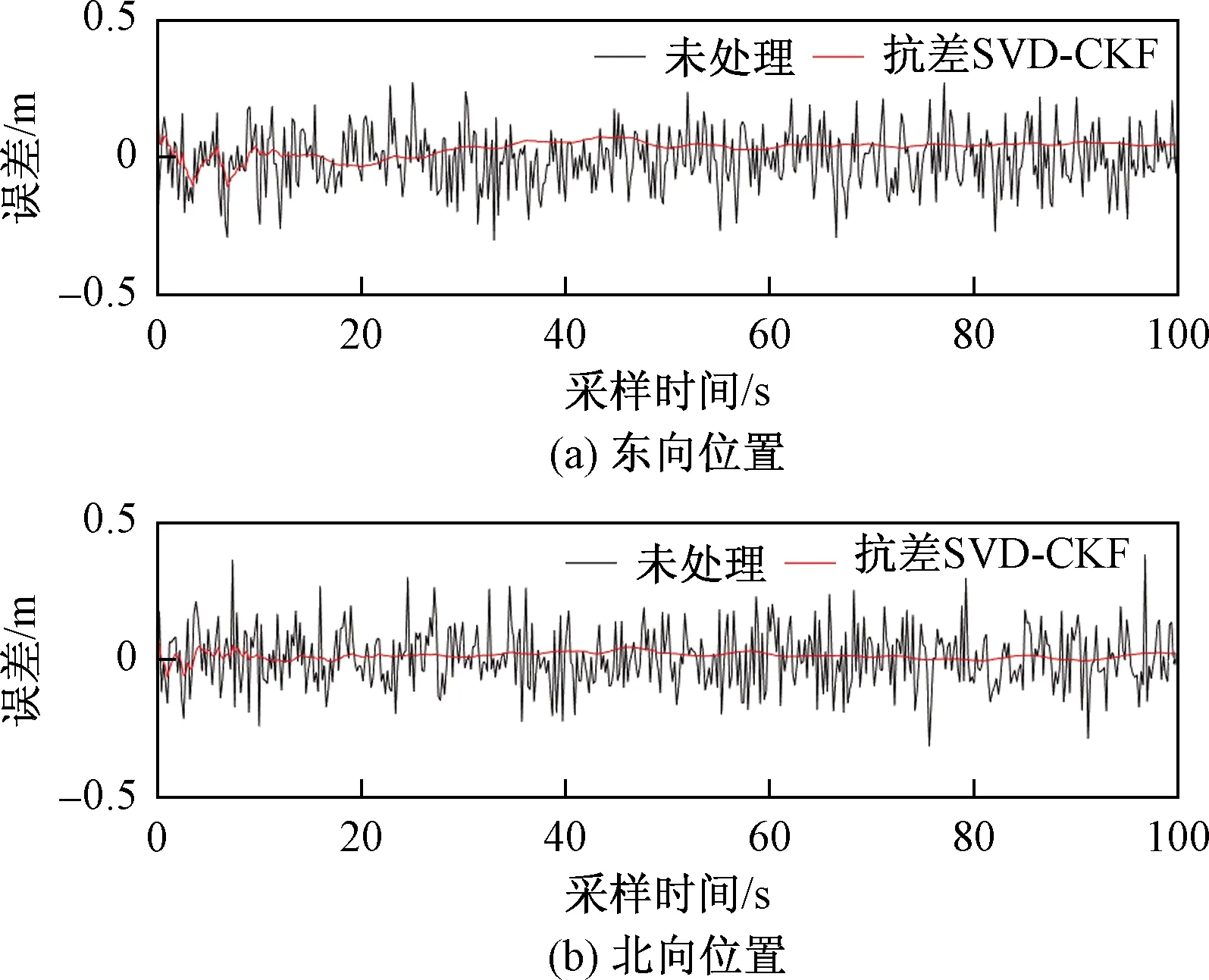
图5 抗差SVD-CKF滤波后位置误差Fig.5 Position error after robust SVD-CKF filtering
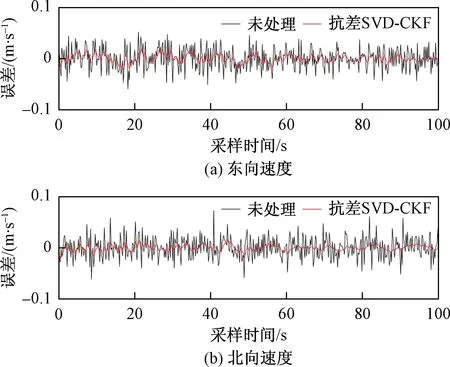
图6 抗差SVD-CKF滤波后速度误差Fig.6 Velocity error after robust SVD-CKF filtering
两种算法的误差统计对比结果如表1所示,抗差SVD-CKF算法的标准差均优于传统CKF算法,经抗差SVD-CKF算法滤波后的数据具有更平稳的性能。
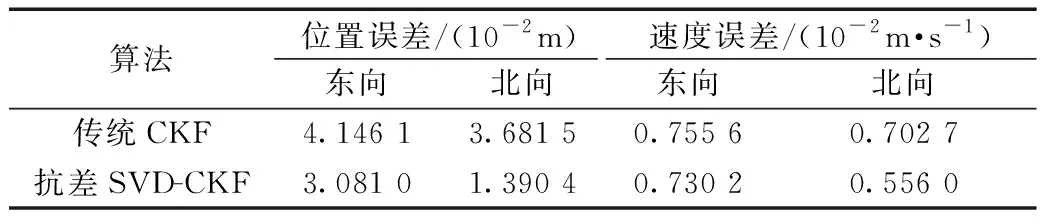
表1 传统CKF和抗差SVD-CKF的标准差比较Table 1 Standard deviation comparison between traditional CKF and robust SVD-CKF
3.2 改进的抗差SVD-CKF抗差效果分析
为了更好地验证改进的抗差SVD-CKF算法在减小异常观测值干扰的效果,考虑到GPS系统在失锁时没有信号,数据传输异常的情况以及割草机平台打滑导致速度突变的状况,以东向位置和东向速度为例,人为地在数据中加入异常观测值,加入异常后如图7所示。
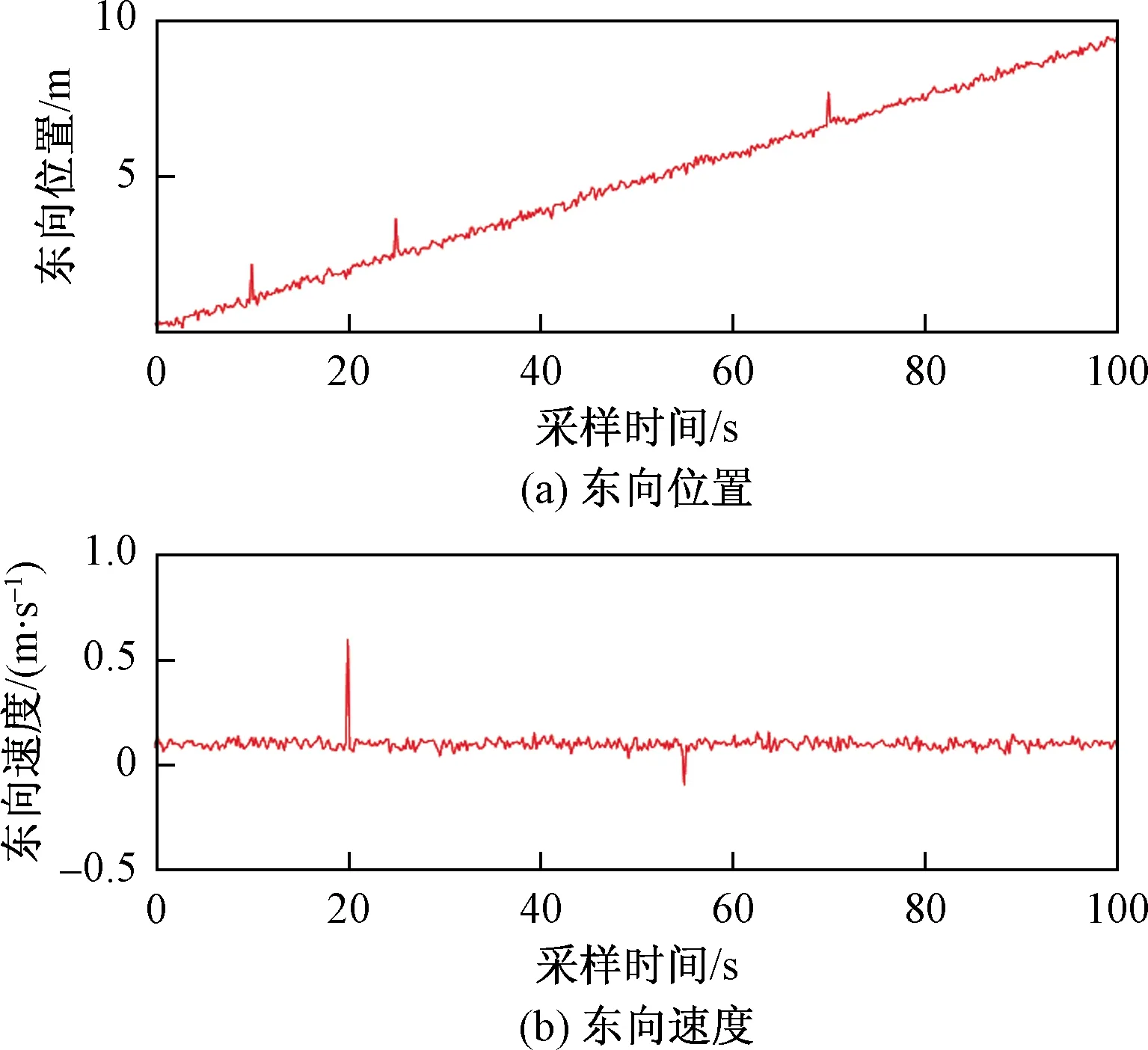
图7 东向加入异常后观测值Fig.7 Observation after adding anomalies to the east
(1)位置异常:在东向位置观测值10、25、70 s处加入2 m的观测粗差。
(2)速度异常:在东向速度观测值20 s处加入0.5 m/s的观测粗差,在55 s处加入-0.2 m/s的观测粗差。
在仿真实验中,均值滤波选取的窗口长度N=5,抗差方法中的阈值选取k0=2,k1=4。加入异常观测值后,其经过传统CKF算法处理和改进的抗差SVD-CKF算法的处理后,异常点处的误差值如表2所示,东向位置误差和东向速度误差对比如图8所示。
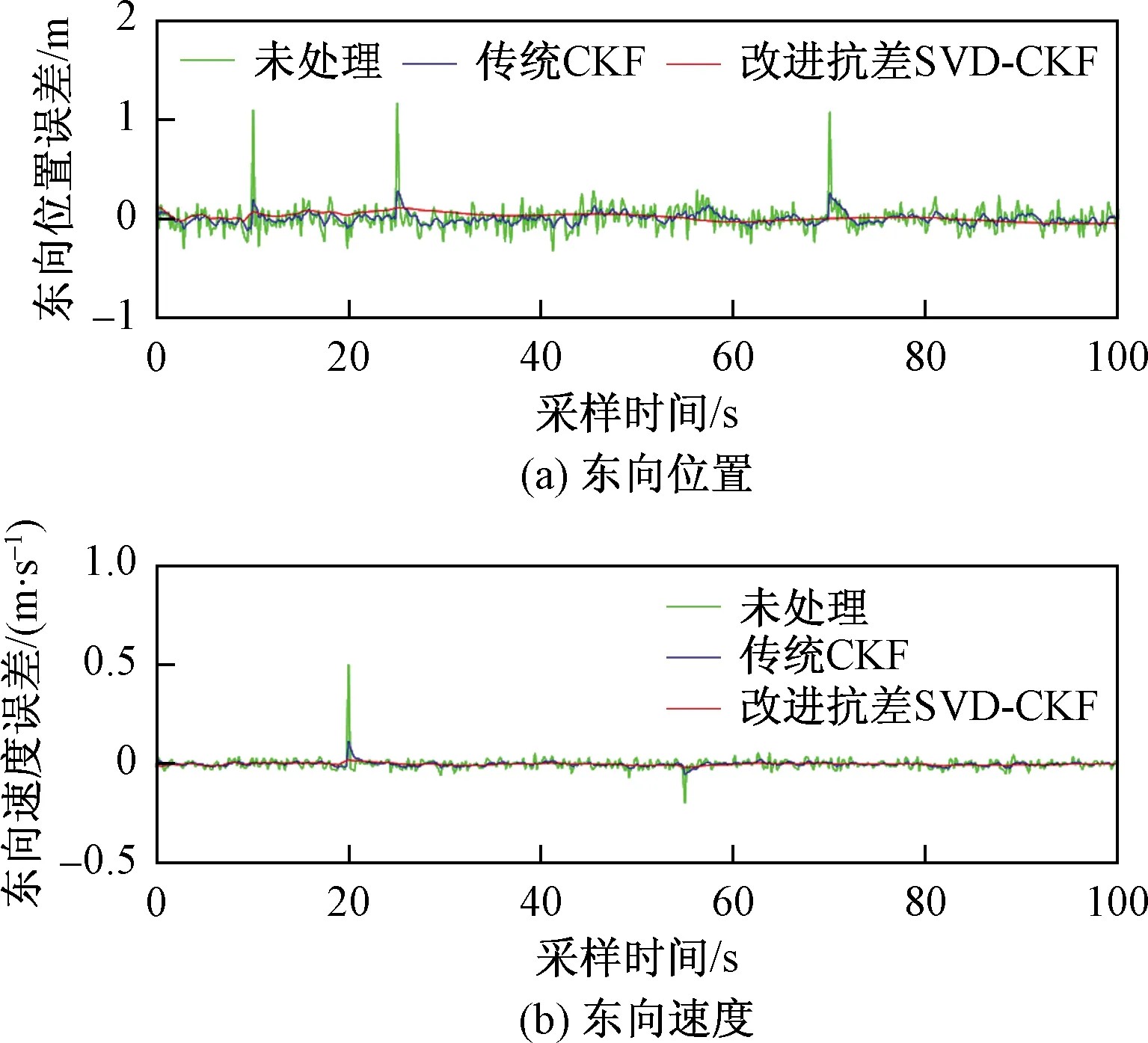
图8 传统CKF和改进抗差SVD-CKF处理结果对比Fig.8 Comparison of traditional CKF and improved robust SVD-CKF processing results
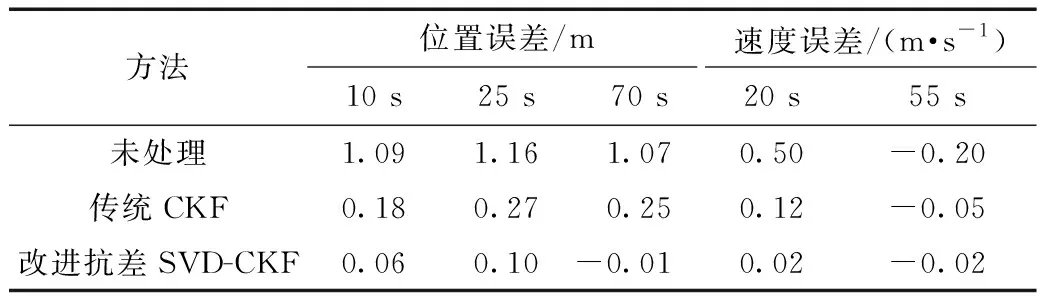
表2 异常点处误差比较Table 2 Comparison of errors at abnormal points
可以看出,传统CKF算法对于异常观测值有一定的抑制效果,但是在出现异常时,产生的误差波动仍然较大;改进的抗差SVD-CKF算法在初始状态波动较大,运行一段时间后,即使遇到异常观测值,也能迅速回到一个较为平稳的状态,其对异常观测值的校正能力相对传统CKF算法要更强。
放大速度误差0~40 s时间段的滤波处理结果如图9所示。
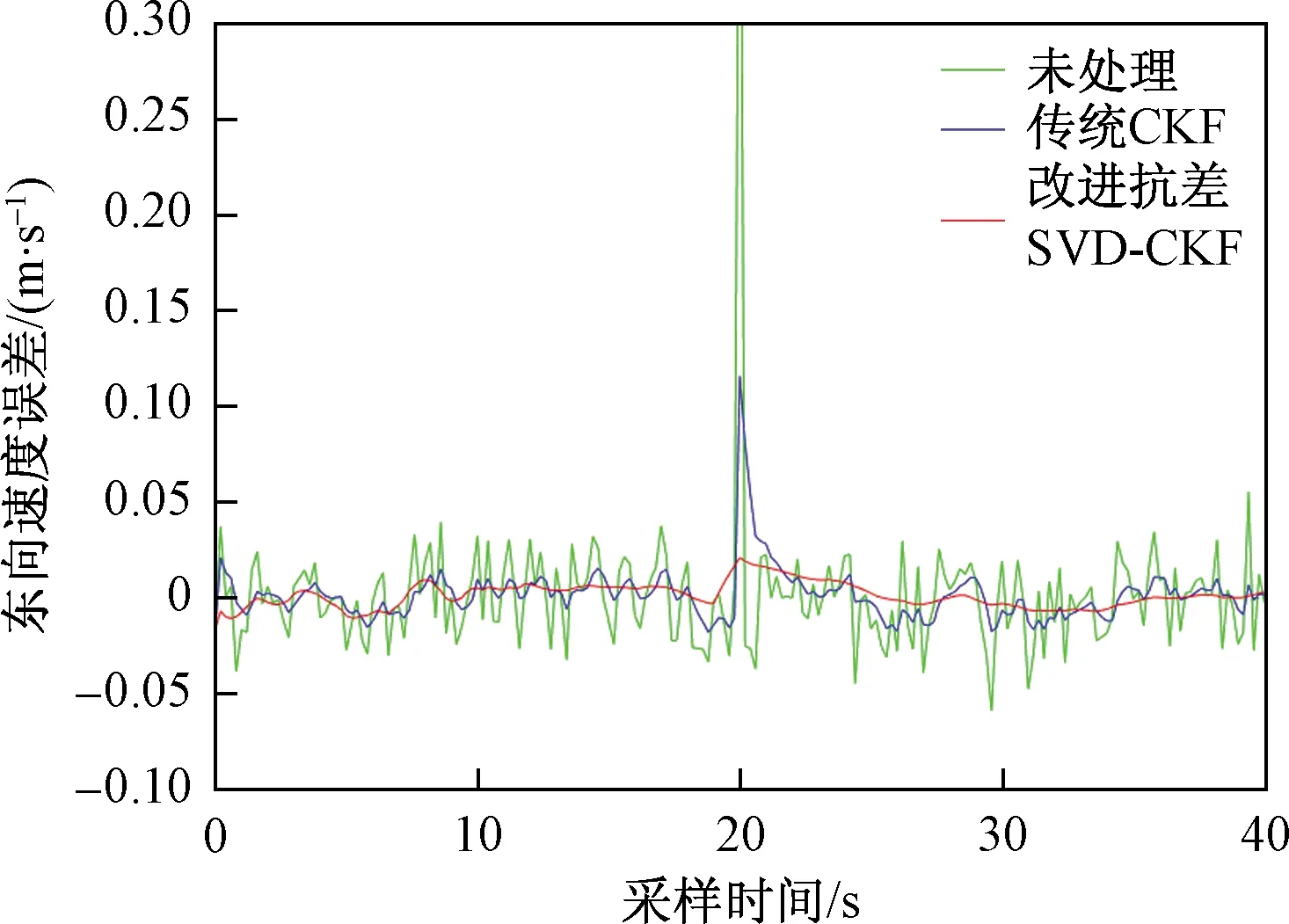
图9 0~40 s东向速度误差对比结果Fig.9 0~40 s east speed error comparison result
由于有均值滤波预处理,当遇到异常观测值时,滤波器可以及时作出响应,同时减弱大幅异常观测值的干扰,减小了数据的波动性,使其能较快恢复到平稳的状态,保证了后续迭代运算的准确性。而没有经过均值处理和抗差算法处理的CKF算法,虽然一定程度上对异常观测值有修正效果,但是需要较长的时间恢复到稳定状态。
4 结论
提出一种改进的抗差SVD-CKF算法,经过仿真分析得到以下结论:
(1)均值滤波预处理对异常观测值有较好的抑制作用,能及时降低异常观测值所带来的影响。
(2)SVD分解有效避免了先验协方差矩阵负定导致滤波发散的情况,增强了滤波稳定性,保证了滤波器的持续运行。
(3)改进的SVD-CKF算法相较于传统CKF算法有效降低了观测数据的波动性,状态更新值保持在一个相对稳定的状态,能够提高GPS导航的精度。

