脂润滑高速角接触球轴承外圈热特性分析及试验

张强强, 张 长

(青海大学机械工程学院, 西宁 810016)

角接触球轴承广泛应用于交通运输、机床、工业生产、航天及精密仪器等领域。在高转速工况下,轴承内部各元件及润滑剂之间的摩擦生热加剧,导致温度上升,进而加剧轴承磨损,降低轴承的使用性能。因此研究高速角接触球轴承的热特性具有重要意义。

角接触球轴承的发热状况与轴承的结构、所受载荷、旋转速度、润滑剂类型以及轴承的安装环境和工作状况有关。程庆元等[1]建立了基于整体法的轴承发热量计算模型和轴承热交换模型,得到了在中低速条件下角接触球轴承的各节点温度；Zheng等[2]研究了角接触球轴承的热性能,得到了温升与转速的关系；Blanuša等[3]给出了圆柱滚子轴承的计算模型及轴承计算的传导和对流换热系数,还确定了轴承特征点在稳态热载荷、最大应力和轴承寿命下的位移；Wu等[4]建立了主轴系统温度场的数学模型,分析了主轴的温度场分布；Rabréau等[5]通过试验对比不同的轴承运动模型,研究了轴承运动学对轴承生热的影响；罗哉等[6]选取轴承外圈为分析对象建立了轴承温升模型,研究了在不同工况条件下轴承外圈的温升情况；刘俊峰等[7]根据Palmgren经验公式计算摩擦热量,并用传热学理论建立了热网络模型,测量了不同工况条件下的外圈温度,结果表明该理论模型能较为准确地预测轴承的温升情况；王亚珍等[8]用热网络法和有限元法分析了柔性轴承,得到了其较为准确的温度场分布。

上述文献主要采用整体法生热模型,研究中低转速工况下轴承的温升情况,在高转速下,滚珠自旋生热量急剧增加,此生热模型已不再适用。现以高速脂润滑角接球轴承为对象,首先分析轴向载荷条件下滚珠的受力和运动,建立含滚珠自旋摩擦的生热模型,其次通过热网络法,建立针对脂润滑条件的传热模型,通过试验比对,验证此生热和传热模型预测轴承外圈温升的准确性,以期为脂润滑高速角接触球轴承的热特性分析及优化设计提供参考。

1 轴承生热模型

1.1 轴承受力分析

为了简化轴承在运动工况下的分析变形,采用刚性套圈理论,即在载荷作用下内外圈滚道不发生结构变形,只存在刚体位移。图1所示为在高转速、受轴向载荷工况下,考虑离心力和陀螺力矩的影响,根据刚性套圈理论建立的滚珠受载前后的滚珠及沟曲率中心几何位置关系。

fi、fo分别为内滚道和外滚道的沟曲率系数；δi、δo分别为内圈和外圈的接触变形；δa为轴向位移；X1、X2为引入的新变量；A1、A2分别为内外沟曲率中心的相对轴向位移和径向位移；D为滚珠直径；α0为滚珠初始接触角；αi、αo分别为内接触角和外接触角图1 滚珠中心及沟曲率中心位置关系Fig.1 Relationship between center of ball and center of groove curvature

根据图1列出方程为

(A1-X1)2+(A2-X2)2-[(fi-0.5)D+

δi]2=0

(1)

(2)

轴承工作过程中,由于滚珠在高速旋转,滚珠的受力情况变得复杂,不仅存在离心力和陀螺力矩,滚珠与内外圈还存在接触载荷,这些都影响着轴承的运动状态。图2所示为受轴向载荷作用下轴承运动时滚珠的受力情况。

Ki、Ko分别为滚珠与内外圈的载荷—变形系数；λi、λo分别为滚珠与内滚道和外滚道的沟道控制系数；Mg为陀螺力矩；Fc为滚珠离心力图2 滚珠受力情况Fig.2 The force situation of ball

根据滚珠的受力情况，列出水平方向与竖直方向上的力平衡方程为

(3)

(4)

轴承在受轴向力的情况下,每个滚珠受力相同,建立整个轴承的平衡方程为

(5)

式(5)中：Fa为轴向载荷；Z为滚珠个数。

对式(1)～式(5)采用Newton-Raphson迭代法求解[9],用MATLAB软件编写了相关程序,求解流程如图3所示,H7008C轴承结构参数如表1所示。

表1 H7008C轴承结构参数Table 1 H7008C bearing structure parameters

图3 非线性方程组求解流程Fig.3 Processing of solving nonlinear equations

转速为12 000～21 000 r/min,轴向载荷在230、290、350 N选择,运用MATLAB迭代求解的轴承接触角、接触载荷和轴向位移规律如图4～图6所示。

图4所示为转速与内外接触角的关系,随着转速的增加,离心力变大,导致内接触角变大,外接触角变小。

图4 转速对接触角的影响Fig.4 Effect of rotational speed on contact angle

图5所示为转速和轴向力对接触载荷的影响。转速增加,滚珠的离心力增大,滚珠与外圈的接触载荷变大,而与内圈的接触载荷变小,且因为离心力的影响,外接触载荷始终大于内接触载荷。轴向载荷增加,滚珠受力增大,接触载荷增加。

图5 转速和轴向力对接触载荷的影响Fig.5 Effect of rotational speed and axial force on contact load

图6所示为转速、轴向力与轴向位移的关系。随着转速的增加,轴向位移减小。轴向载荷的增加,受力增大, 轴向位移则会增大。

图6 转速和轴向载荷对轴向位移的影响Fig.6 Effect of rotational speed and axial load on axial displacement

1.2 轴承运动分析

对于机床主轴的支撑轴承,其内圈旋转,外圈固定,滚珠的公转角速度ωm的计算式为

(6)

自转角速度ωR的计算式为

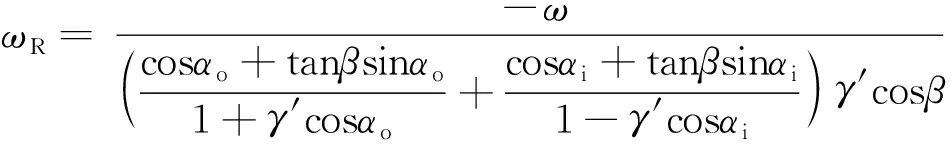
(7)

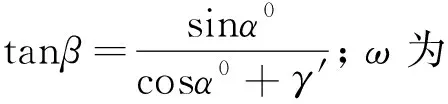
根据外沟道控制理论,滚珠在外圈做纯滚动,内圈则发生自旋。滚珠的自旋角速度ωsi的计算式为

(8)

对轴承进行受力分析及运动分析,得到轴承内部各元件的接触载荷、接触角等力学参数和滚珠的公转、自转、自旋等运动学参数,可为轴承内部的摩擦生热分析提供基础。

图7所示为滚珠公转、自转、自旋速度与主轴转速关系。从图7中可以看出,主轴转速上升,自转速度上升最快,公转速度上升最慢,自旋速度位于两者之间。

图7 滚珠公转、自转、自旋速度与主轴转速关系Fig.7 Relationship between ball rotation speed, spinning speed and spindle speed

1.3 生热模型的建立

轴承的产热主要是自身的摩擦力矩引起的,摩擦力矩越大,产生的热量越多[10]。通过计算摩擦功耗的方式来计算生热量。整体法生热模型主要用于中转速轴承生热计算[11],在轴承高速运转时,滚珠的自旋摩擦占据很大一部分,所以在整体法生热模型的基础上考虑滚珠自旋摩擦热,可以建立更精确的、高转速的角接触球轴承生热模型。

1.3.1 整体法生热模型

Palmgren[12]通过对不同类型、不同尺寸轴承的大量试验,总结出了计算轴承摩擦力矩的计算公式,其摩擦力矩分为两部分,分别为润滑引起的摩擦力矩M和轴承载荷引起的摩擦力矩Ml,对于中等转速、润滑正常的角接触球轴承,由润滑引起的摩擦力矩M计算公式为

(9)

式(9)中：f0为与润滑有关的系数,脂润滑取2,油润滑取1；n为主轴转速。

由载荷引起的摩擦力矩Ml计算公式为

Ml=f1Fβdm

(10)

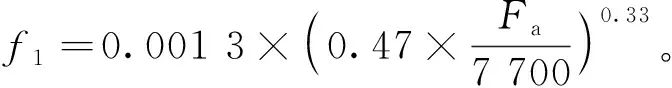
Palmgren计算法(即整体法)的摩擦生热量Hp的计算式为

(11)

1.3.2 考虑滚珠自旋生热模型

根据外沟道控制理论,即滚珠在与内外圈接触时,滚珠只在内圈发生滚动和自旋,而在外圈做纯滚动,单个滚珠的内圈自旋摩擦力矩Msi的计算公式为

Msi=3μQiaiEi/8

(12)

式(12)中：Msi为自旋摩擦力矩；μ为滑动摩擦系数；Qi为内接触载荷；ai为滚珠与内圈接触椭圆长轴；Ei为第二类完全椭圆积分。

自旋的摩擦生热量Hsi的计算式为

Hsi=MsiωsiZ

(13)

考虑滚珠自旋的总摩擦热Hs为

Hs=Hp+Hsi

(14)

图8所示为两种模型生热量比较。由图8可看出,随着转速的增加,含滚珠自旋摩擦的生热量快速上升,整体法模型生热量上升缓慢。生热量差距体现在滚珠自旋摩擦热上,这是由于在高转速时,自旋速度快速上升,自旋生热量快速增加,滚珠的自旋摩擦生热不可忽略。

图8 两种生热模型的总生热量Fig.8 Total heat generation in two heat generation models

2 轴承传热模型

2.1 对流换热系数

Harris等[9]给出的对流换热系数α的计算公式为

(15)

式(15)中：α为对流换热系数；K为润滑剂导热系数；x为特征长度；Pr为普朗特数,取值范围在 0.6～200；Re为雷诺数,Re=ux/v0,取值范围在1×104～5×105。

在轴承系统中,轴承座是静止状态,轴承与空气之间的对流换热系数为9.7 W/(m2·℃)[13]。

由式(15)计算在轴向载荷为350 N,转速为12 000～21 000 r/min时,轴承的内圈对流换热系数α1、外圈对流换热系数α2、滚珠对流换热系数α3如表2所示。

表2 对流换热系数Table 2 Convection heat transfer coefficient

2.2 热流分析

2.2.1 温度节点系统

根据H7008C角接触球轴承的基本结构,建立了温度节点系统，如图9所示。根据Burton等[14]提出的观点,轴承生热量一半进入滚珠,一半传到内外圈上。

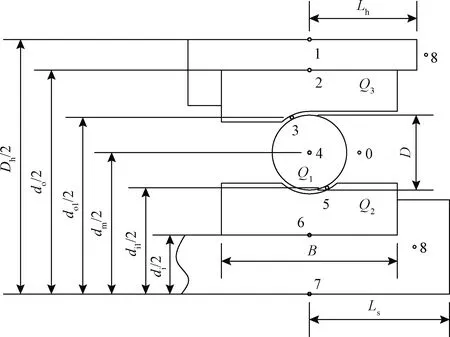
Q1为传入滚珠的热量；Q2为传入内圈热量；Q3为传入外圈热量；0为润滑脂温度节点(已知)；1为轴承座温度节点；2为轴承外圈温度节点；3为外滚道温度节点；4为滚珠温度节点；5为内滚道温度节点；6为轴承内圈温度节点；7为主轴温度节点；8为空气对流温度节点(已知)图9 轴承温度节点系统Fig.9 Bearing temperature nodes system

2.2.2 温度传递系统

热网络法是建立轴承各部分元件温度节点,根据能量平衡原理,流入该节点的能量等于流出该节点的能量,每个节点之间以热阻的形式关联形成热网络。图10所示为建立的温度传递系统,其中,热量Q1传入节点4,即传入滚珠；热量Q2传入节点5,即传入内圈；热量Q3传入节点3,即传入外圈。

箭头表示热量传递的方向；Rvab表示传导在a、b之间发生；Rcab表示对流在a、b之间发生图10 轴承温度传递系统Fig.10 Bearing temperature transfer system

2.3 系统方程

图9、图10建立的温度节点系统和温度传递系统,可建立以7个未知节点温度为求解对象的热平衡方程。运用MATLAB数值解法,得到温度T2即为轴承外圈温度。

(16)

2.4 热阻计算

表3 传导或对流热阻计算公式Table 3 Calculation formula for conduction or convection thermal resistance

3 试验

3.1 试验装置及流程

图11所示为测量轴承外圈温度的试验装置。轴承安装在主轴上,主轴的转速由伺服电机提供,轴承内圈与主轴转速同步,轴向加载装置加载在轴承外圈上,加载方式为液压加载,温度传感器插入轴承座孔中测量轴承外圈温度。

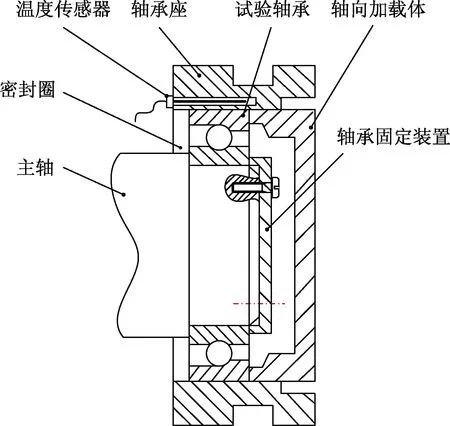
图11 轴承外圈温升试验装置Fig.11 Test device for temperature rise of outer ring of bearing

试验流程如图12所示。编写S7-200程序,控制伺服电机AKM2G和液压加载装置,分别提供主轴转速范围为12 000～21 000 r/min,轴向载荷为350 N,温度传感器PT100探头插入轴承座孔中,末端连接移动式数据采集系统QUANTUMX CX22B-W,采集轴承外圈温度。

图12 试验流程Fig.12 Processing of test

3.2 试验结果

本次试验轴承为H7008C角接触球轴承,采用润滑脂为复合锂皂L252,测量温度为轴承外圈温度,施加轴向载荷为350 N,转速分别为12 000、15 000、18 000、21 000 r/min,每种转速测试时间为300 s,温度记录频率为30 s一次,试验结果如图13所示。

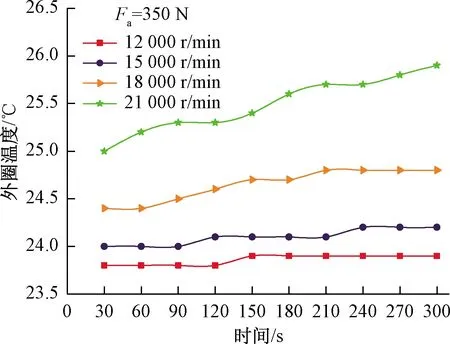
图13 外圈温升试验结果Fig.13 Results of outer ring temperature rise

4 结果比对分析

润滑脂温度T0、空气温度T8、试验温度T、含滚珠自旋摩擦计算温度Ts和整体法生热模型计算温度TP与转速n的关系如图14所示。由图14可看出,含滚珠自旋的外圈温度值始终高于整体法生热模型的计算温度,且更接近于试验值。在轴向载荷为350 N,转速从12 000 r/min上升到21 000 r/min时,试验温度上升了1 ℃,含滚珠自旋生热模型温度上升了0.23 ℃,整体法计算法温度上升了0.07 ℃。

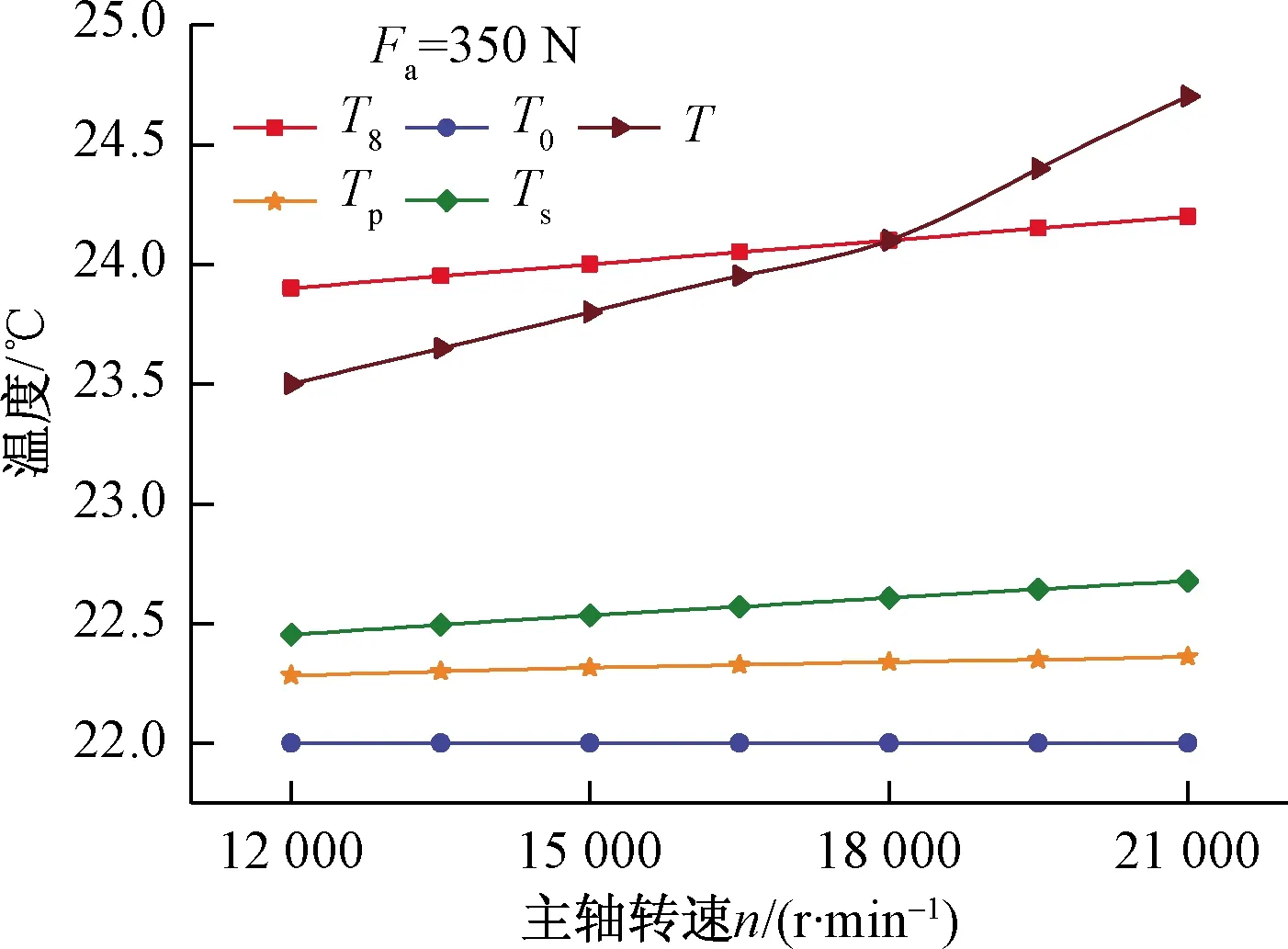
图14 结果比较Fig.14 Results comparison

两种生热模型与试验的误差如表4所示，可以看出,转速从12 000 r/min上升到21 000 r/min,含自旋摩擦热的计算模型得到的结果与试验值的误差从4.88%上升到8.25%,误差增大了3.37%,整体法生热模型计算的结果与试验误差从5.68%上升到9.79%,误差增大了4.11%。在同种转速下,含滚珠自旋摩擦生热计算的温度与试验误差总小于整体法计算法与试验的误差。

表4 误差分析Table 4 Error analysis

5 结论

建立高速脂润滑角接触球轴承含滚珠自旋摩擦热的生热及传热模型,计算得到轴承外圈的理论温度,与实验结果比对,得到以下结论：

(1)高速脂润滑角接触球轴承的受力和运动受转速影响较大,转速上升,内接触角、外接触载荷、滚珠公转、自转和自旋速度随之增大,外接触角、内接触载荷、轴向位移随之减小。

(2)高转速下滚珠的自旋对生热的影响不可忽略,在转速达到21 000 r/min时,自旋生热量已经超过总生热量的50%,成为轴承生热的主要方式。

(3)两种模型的计算温度与试验温度比对,考虑滚珠自旋摩擦热的生热模型及传热模型得到的外圈温度更接近于试验温度,且误差在9%以内,证明了此模型分析计算外圈温升的准确性。