基于光滑逼近函数的高阶牛顿法求解凸二次规划

雍龙泉, 贾 伟, 黎延海

(1.陕西理工大学数学与计算机科学学院, 汉中 723001； 2.陕西理工大学, 陕西省工业自动化重点实验室, 汉中 723001)

凸二次规划(convex quadratic programming,CQP)是非线性规划中的一类特殊数学规划问题,在很多方面都有应用,如投资组合、支持向量机等[1-5]。鉴于求解凸二次规划是模式识别、机器学习等领域的关键环节,因此(大规模稀疏)凸二次规划一直是优化理论的研究热点。求解二次规划常见方法有:拉格朗日方法、Lemke方法、内点法、有效集法和椭球算法等[6-11]。自从1984年印度著名数学家Karmarker提出了内点算法以来,由于该算法具有多项式复杂性,而且实际计算效果较为良好,经过多年的研究,凸二次规划的原对偶内点算法以及核函数内点算法已经成功地被推广到求解半定优化、互补问题、锥规划等优化问题。凸二次规划已经成为运筹学、经济数学、人工智能、机器学习等领域的基本方法。

尽管内点算法具有多项式迭代复杂性,但是每次计算下降方向时采用牛顿方向:即计算一个齐次线性方程组的非零解。这其中需要计算雅克比矩阵及其逆矩阵,雅克比矩阵的非奇异性保证了齐次线性方程组解(下降方向)的存在唯一性。 而实际问题的雅克比矩阵往往是一个高维的稀疏矩阵,其行列式或特征值难以计算,因此雅克比矩阵的非奇异性难以证明,相应的齐次线性方程组求解也不是太容易,这也是目前内点算法的瓶颈。

为克服各类内点算法中计算瓶颈,即不考虑牛顿方向。给出求解凸二次规划的新方法：通过将凸二次规划转化为非线性方程组,进而采用逼近程度较好(且不易发生溢出的)光滑逼近函数进行处理,得到光滑非线性方程组,再采用三步迭代牛顿法进行求解。

1 光滑逼近函数

定义1给定非光滑函数f(t):R→R,称光滑函数fμ(t),μ>0为f(t)的光滑逼近函数,如果对任意t∈R,存在κ>0,使得|fμ(t)-f(t)|≤κμ,∀μ>0，如果κ不依赖于t,则称fμ(t)为f(t)的一致光滑逼近函数。

一致光滑逼近函数可以分为从上方一致逼近和从下方一致逼近[12]。文献[13]给出绝对值函数φ(t)=|t|的光滑函数:

(1)

(2)

(3)

3个一致光滑逼近函数的性质如下。

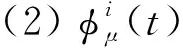
(4)

(3)对于∀t∈R,有

(5)

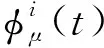
图1 μ=0.4时与φ(t)=|t|的图像Fig.1 Graph of and φ(t)=|t| with μ=0.4

图2 μ=0.2时与φ(t)=|t|的图像Fig.2 Graph of and φ(t)=|t| with μ=0.2

2 凸二次规划光滑处理

考虑凸二次规划及对偶二次规划(dual quadratic programming,DQP)。

(1)CQP：

(6)

(2)DQP:

(7)

式中：Q∈Rn×n为对称的半正定矩阵；c∈Rn；z∈Rn;A∈Rm×n;b∈Rm;w∈Rn;y∈Rm;m≤n,且rank(A)=m,其最优性条件为

(8)

令z=|x|-x,w=|x|+x,则最优性条件等价于非线性方程组:

(9)

记向量绝对值函数φ(x)=|x|=(|x1|,|x2|,…,|xn|)T的每一个分量为φ(xi)=|xi|,i=1,2,…,n。

对每一个φ(xi),采用定理1中的光滑函数

(10)

进行光滑化处理,这样就得到向量绝对值函数φ(x)的光滑逼近函数为

φμ(x)=[φμ(x1),φμ(x2),…,φμ(xn)]T

(11)

且每一个分量φμ(xi)满足0<φμ(xi)-φ(xi)≤μ,i=1,2,…,n。

从而有

(12)

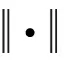
通过光滑处理,问题[式(9)]转化为光滑方程组:

0

(13)

定理2对任意的μ>0,Fμ(x,y)一致光滑逼近F(x,y)。

证明任意的μ>0,

Fμ(x,y)-F(x,y)=

(14)

引理1 设矩阵A∈Rm×n,rank(A)=m,D=diag(d1,d2,…,dn), |di|<1,i=1,2,…,n。Q∈Rn×n为对称半正定矩阵,I表示单位矩阵,则矩阵

(15)

是非奇异的。

证明令X=-(I+D)(I-D)-1-Q,其中，-X为正定矩阵,故X可逆。则有

(16)

故G的非奇异性等价于-AX-1AT的非奇异性。

由于-X=(I+D)(I-D)-1+Q为正定矩阵,结合rank(A)=m可知，A(-X-1)AT为正定矩阵,从而-AX-1AT非奇异,也即G非奇异。

记Fμ(x,y)的Jacobian矩阵F′μ(x,y), 简单运算可得

(17)

式(17)中：

(18)

定理3设Q∈Rn×n为对称半正定矩阵,A∈Rm×n,rank(A)=m,则对∀μ>0,Fμ(x,y)的Jacobian矩阵F′μ(x,y)非奇异。

证明根据定理1,则有

(19)

结合引理1可知,F′μ(x,y)非奇异。凸二次规划的最优性条件[式(18)]已经转化为光滑非线性方程组[式(13)],给出求解光滑非线性方程组[式(13)]的高阶牛顿法。

3 高阶牛顿法

(1)输入。矩阵Q∈Rn×n,A∈Rm×n, rank(A)=m,b∈Rm,c∈Rn；设定常数μ和终止条件ε；取x(0)∈Rn,y(0)∈Rm；令p=0。

(2)开始计算。

X(p)=(x(p),y(p))

(20)

(21)

Fμ(X(p))=

(22)

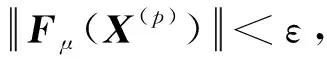
(23)

F′μ(X(p))=

(24)

(25)

V(p)=X(p)-[F′μ(U(p))]-1Fμ(X(p))

(26)

X(p+1)=V(p)+{[F′μ(X(p))]-1-

2[F′μ(U(p))]-1}Fμ(V(p))

(27)

X(p)=X(p+1),p=p+1,转式(20)。

(3)输出计算结果。

z*=|x(p)|-x(p),w*=|x(p)|+x(p),y*=y(p)

(28)

文献[16]证明了该方法在求解非线性方程组时具有五阶收敛速度；文献[17]应用该方法求解了线性规划,首次把该方法应用于求解凸二次规划。在实际计算过程中,若雅克比矩阵接近奇异,可以采用阻尼牛顿法处理。

4 数值实验

采用牛顿法求解凸二次规划的问题,程序采用MATLAB R2009a编写。设置μ=1×10-3,x(0)=0∈Rn,y(0)=0∈Rm,终止条件ε=1×10-6。

算例1考虑如下凸二次规划：

(29)

算法经过2次迭代,得z*=(1.129 0, 0.774 2, 0.096 8, 0)T,w*=(0, 0, 0, 1.032 3)T,y*=(0, -1.032 3)T,相应的目标值为-7.161 3。

算例2考虑如下凸二次规划:

(30)

算法经过2次迭代,得z*=(1, 1, 0)T,w*=(0, 0, 2)T,y*=-2,相应的目标值为-6。

算例3考虑如下凸二次规划：

(31)

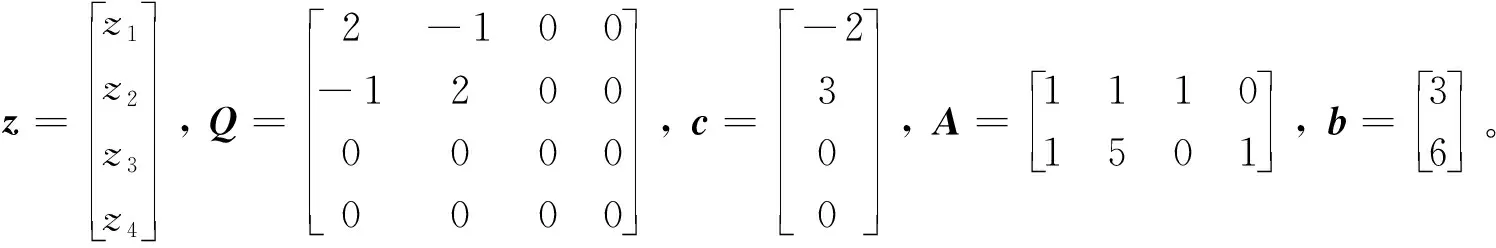
算法经过3次迭代,得z*=(1, 0, 2, 5)T,w*=(0, 2, 0, 0)T,y*=(0, 0)T,相应的目标值为-1。

算例4考虑如下凸二次规划：

(32)

算法经过3次迭代,得z*=(0, 0, 5)T,w*=(0, 4, 0)T,y*=0,相应的目标值为0。

算例5考虑如下凸二次规划：

(33)

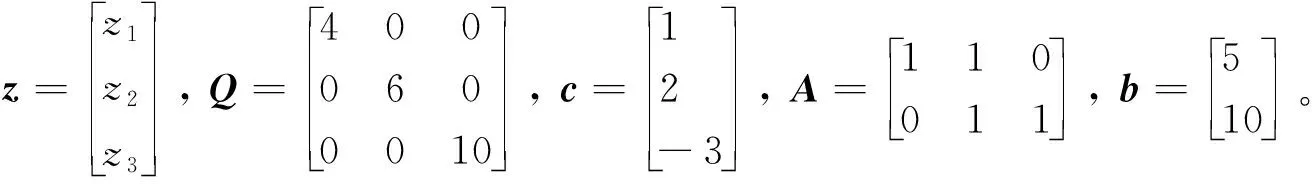
算法经过2次迭代,得z*=(0, 5, 5)T,w*=(16, 0, 0)T,y*=(-15, 47)T,相应的目标值为195。

算例6考虑如下凸二次规划：

(34)

算法经过2次迭代,得z*=(6.333 3, 5, 11.666 7, 0)T,w*=(0, 0, 0, 4.666 7)T,y*=(-0.666 7, 4.333 3)T,相应的目标值为-168.166 7。

5 结论

通过把凸二次规划转化为非线性方程组,采用光滑逼近函数进行处理,得到光滑非线性方程组,进而利用高阶牛顿法进行求解,选用的牛顿法具有五阶收敛性；进一步可以构造逼近程度更好的一致光滑函数,采用更高阶的牛顿法[18-24]进行求解。