含气地层不均匀沉降对盾构隧道结构影响的固-液-气耦合分析

王晖皓, 叶 斌*, 涂新斌, 钱玉华, 程子睿

(1.同济大学土木工程学院, 上海 200092； 2.国家电网有限公司, 北京 100031；3.江苏省送变电有限公司, 南京 211100)

在中国沿海地区的地下工程施工过程中,经常发现富含高压气体的地层。这些气体的主要成分为甲烷,且埋深较浅,被称为浅层沼气。例如,杭州地铁1号线穿越了含浅层沼气的地层,为此在施工过程中采取了专门的应对措施[1]。浅层沼气在软土中多以气囊或气层的形式存在。地下工程开挖将引起土体扰动,进而打破水-土-气的三相平衡状态,导致浅层沼气的渗流或排出。在气体渗流或排出过程中,土体骨架、地下水和浅层气三相间将发生相互作用,引起土体变形甚至产生不均匀沉降,有可能对隧道结构的安全性造成威胁[2]。因此,为了保证隧道的安全运营,有必要研究含气地层的不均匀沉降对盾构隧道结构的影响。

由于地层条件的复杂性,数值模拟方法通常被用于研究隧道的结构稳定性问题。近年来，考虑多相耦合的有限元方法逐渐兴起[3]，该方法已被广泛应用于油气开采[4]、二氧化碳地下封存、降雨入渗[5]及核废料处置库存的安全性等领域。Lewis等[6]提出了热-固-液-气耦合模型模拟储层变形和油气开采过程中的两相流动和地面沉降。Nagel等[7]基于BBM(barcelona basic model)模型建立了三相耦合有限元模型,并对压气法隧道施工过程进行了模拟。Rutqvist等[8]将FLAC3D与TOUGH软件相结合,开发了FLAC-TOUGH耦合程序,实现了热-流-固(THM)多相耦合的数值模拟。

针对浅层气体渗流及排出引起的地层沉降问题,许多学者也开展了相关研究工作[9]。钟方杰[10]针对杭州湾大桥工程地质勘探过程中发生的多次强烈井喷现象,应用FLAC2D两相流模块,模拟在含浅层气的地层中进行钻探引发浅层气释放对地层的影响效应。王勇[1]在此基础上,以杭州地铁典型含气区段——钱塘江南岸某地层为背景,应用FLAC2D中的两相流模块,提出了放气路径下储气砂土的本构模型,并对工程放气路径(排气井)下储气砂层变形进行了数值模拟。卢浩等[11]认为气体泄漏引起的地层不均匀沉降将会导致管片受力变形，通过对沉降部分土体进行开挖来模拟气体释放对地层的影响,从而避开了两相流的难点,模拟了气体释放对管片受力变形性能的影响。彭海波[12]在Rutqvist等[13]研究的基础上开发了FLAC-TOUGH接口程序,控制TOUGH2和FLAC3D在数值模拟过程中有序运行并利用耦合关系式传递相关状态变量,克服了FLAC3D不能进行两相流分析计算的缺点,实现了对水-气二相流-固耦合模拟。李晓敏[14]利用TOUGH2和FLAC3D建立水-气-固三相耦合模型实现了对非饱和土边坡的降雨入渗模拟。可以发现,目前的研究工作大多基于已有的商用软件进行模拟,但这些软件大多只考虑两相的作用[15],无法模拟固-液-气三相的共同耦合作用。此外,已有研究的土体本构模型多采用软件自带的简单本构关系(如摩尔-库仑模型等),无法模拟固-液-气三相共存(非饱和状态)土体的复杂力学行为特征。

以苏通气体绝缘金属封闭输电线路(gas-insulated metal enclosed transmission line,GIL)综合管廊项目中盾构隧道穿越的长江江底浅层气体分布区为研究对象,采用自主开发的水-土-气三相渗流-变形耦合有限元程序,并基于Zhang等[16-17]提出的本构模型,模拟了含浅层沼气地层的变形特性,研究了气体渗流及排出引起的地层不均匀沉降对隧道结构受力的影响。

1 计算模型

1.1 工程背景

苏通GIL综合管廊工程位于G15沈海高速苏通长江大桥上游1 km,是“淮南-南京-上海1 000千伏交流特高压交流工程”下穿长江的重要节点,由两岸引接站和GIL管廊组成。其中管廊部分采用盾构法施工穿越长江,隧道所在位置如图1所示。

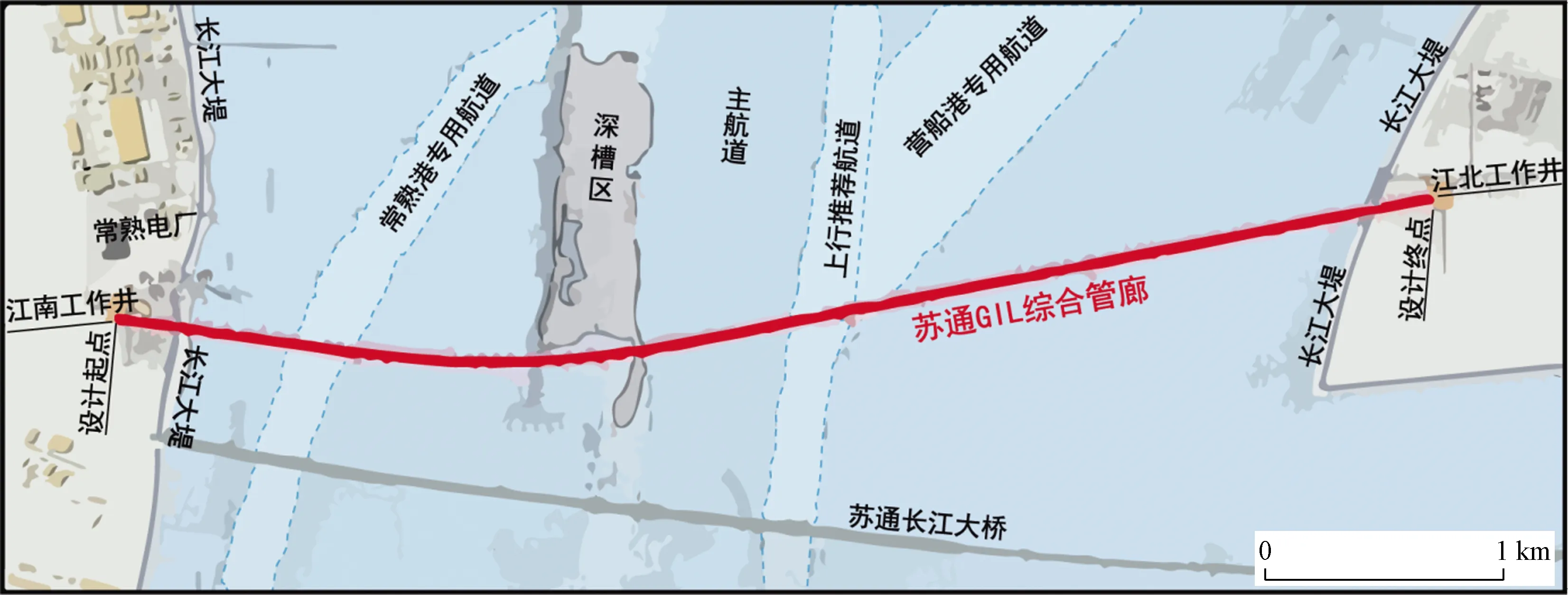
图1 隧道所在位置Fig.1 The location of tunnel

在中国长江中下游及东南沿海地区,沿江、沿海的湖相、河流相及海相的沉积平原中广泛分布有第四系浅层生物气藏,其埋深一般小于100 m。根据《淮南-南京-上海1 000千伏交流特高压输变电工程苏通GIL综合管廊工程施工图有害气体勘察报告》,GIL综合管廊工程的盾构隧道有部分区段位于浅层气体分布区,其推定里程为DK1+0～DK1+780,如图2所示。地层中存在这些浅层气的成分甲烷(CH4)占比(85%～88%)、氮气(N2)占比(8%～10%)、氧气(O2)占比(2%～3%),为生物成因浅地层天然气,成团块状、囊状局部集聚分布,气体压力约为0.4～0.9 MPa,气藏类型为原生超浅层微气藏,有害气体在土层中呈扁豆体状、团块状、囊状、蜂窝状不连续分布,气、水同层,在淤泥质、粉质黏土层中以团状气包的形式存在。隧道开挖将导致原有气囊失衡,多个沼气气囊出现运移,有可能形成连续的含气地层。根据地质勘察资料,分布区(DK1+0～DK1+780)地层由上至下依次分布有：③淤泥质粉质黏土层、④1粉质黏土混粉土层、④2粉砂层、⑤1粉细砂层、⑤2粉砂层、⑥1中粗砂层、⑦1粉细砂层、⑧1中粗砂层及⑧2粉细砂层。地层顶部距离自由海平面约7.0 m,隧道标高为-40.0～-51.6 m,中心标高为-48.5 m。

图2 有害气体分布区Fig.2 Harmful gas distribution aera

1.2 有限元模型

为了实现含气地层在三维地层模型中固-液-气三相耦合数值模拟计算,对上述地层进行概化并做如下假设简化:①土层分布均匀且水平分布,气压分布均匀且各向同性；②地下水位取地表高程；③含气地层位置紧贴隧道底面。

实际场地中所涉及的地层数较多,但部分土层物理性质相近,参数相差不大。因此,为简化模拟计算步骤,提高模拟计算效率,将实际地层数划分为2类,其中,③淤泥质粉质黏土层、④1粉质黏土混粉土和④2粉砂层划分为第Ⅰ层粉土层,剩余下方地层统一划分为第Ⅱ层细砂层。

简化后的模型断面如图3所示,建模范围取隧道半径的10倍以上以消除边界效应的影响。整个计算分析模型的尺寸的长度方向取131.6 m,宽度方向取100 m,深度方向取105.8 m。隧道外径11.6 m,内径10.5 m,衬砌厚度为0.55 m。由于现场无法获取具体气藏分布尺寸资料,故假设含气地层分布长度取模型长度的1/2为60.7 m,分布宽度取隧道外径长度为11.5 m,而气藏厚度根据勘察报告取15 m。隧道上方布设观察点(U1、U2、U3),隧道下方布设观察点(D1、D2、D3、D4、D5、D6)和观察单元(E1、E2、E3)。图4为三维模型示意图,图5为建立的三维有限元网格模型。

图3 基本地层二维模型及观察点布置Fig.3 Basic soil layer 2D model and the observation points arrangement

图4 三维模型示意图Fig.4 3D model schematic diagram

图5 三维有限元网格Fig.5 3D finite element method mesh

1.3 模型初始条件

渗流场的初始压力条件主要包括初始孔隙水压与初始气压两部分。对于孔隙水压的初始条件,根据实际场地地质钻孔剖面图,设定地层顶部为自由水平面,即自由水面的位置水头为40 m。非含气层初始水压取自由水面下静水压力,则非含气层中某点的初始孔隙水压(pw0)表达式为

pw0=ρwg(40-z)

(1)

式(1)中：ρw为水的密度；g为重力加速度；z为该点的竖坐标。

对于含气层,结合勘察报告静力触探CPTU试验中的部分钻孔孔隙水压消散曲线(图6),初始孔隙水压不含毛细水压力,则含气层的初始孔隙水压p′w0表达式为

图6 孔隙水压消散曲线Fig.6 Pore water pressure dissipation curve

p′w0=ρwg(10-z)

(2)

对于气体压力初始条件,假设气体在含气层以及渗流通道内各处气压连通。根据有害气体勘察报告,含气地层初始气藏压力取900 kPa,初始的水相饱和度设为0.8,非含气层初始的水相饱和度设为最大饱和度,其中粉土层为1.0,细砂层为0.98。为了方便描述,文中饱和度均指水相饱和度。

对于土体应力场,假设隧道开挖前土体处于自重应力场作用。为简化考虑隧道开挖的影响,数值模拟过程分3步进行:①计算完整土体在自重作用下的初始应力场；②去除隧道内的土体单元模拟隧道开挖,并在隧道边界上设置薄板单元模拟衬砌添加,得到隧道开挖后应力场；③将②中得到的土体应力场作为渗流计算的初始应力场,计算沼气渗漏模式下固-液-气三相之间的相互作用。

1.4 模型边界条件

模型上边界设为自由透水透气边界,无位移约束；下边界设为不透水不透气边界并约束z向位移；

左、右侧边界设为不透水不透气边界并约束x向位移；前、后侧边界也设为不透水不透气边界并约束y向位移；隧道边界除渗气口外皆设为不透水不透气边界；其余内部边界均为渗透边界。D1为渗气边界中心,如图7所示。渗气边界为恒定气压边界。

图7 渗气口附近的局部放大图Fig.7 Partial enlargement of the vicinity of the gas permeation port

1.5 模型参数

数值计算采用自开发的有限元计算程序。该程序能够对固-液-气三相渗流-变形进行耦合分析,目前已经在多个岩土工程问题中得到了应用[18-20]。在三相耦合计算中,土层本构关系采用前章介绍的基于修正剑桥的非饱和弹塑性本构模型[16-17]。

模型参数包括基本地层和隧道衬砌材料的物理参数、水力学参数、土水特征曲线参数和剑桥模型基本参数,具体取值如表1～表3所示。地层物理及水力学参数取值主要依据项目的土工试验报告,其中常规参数(如重度、泊松比等)可以直接采用,其他参数根据规范标准进行换算；土水特征曲线参数参考相似性质的土体参数进行取值；剑桥模型基本参数部分取自土工试验报告,其他参数采用相同土类土体的经验值；盾构隧道的衬砌材料按照项目工程结构设计文件选用的混凝土规格确定。

表1 基本地层及隧道衬砌材料的物理及水力学参数Table 1 Physical mechanics and hydraulic parameters of basic soil layer and tunnel lining

表2 土水特征曲线参数取值Table 2 Parameter value of soil water characteristic curve

表3 剑桥模型基本参数Table 3 Parameter value of Cambridge model

2 计算结果分析

盾构隧道在运营过程中容易发生过量的纵向沉降或不均匀沉降,引发隧道结构局部破坏或纵向扭曲变形,影响隧道的正常运营。从隧道竖向位移和截面附加弯矩两方面评价隧道的稳定性,并且通过渗气口饱和度与气压的变化观察气体的渗漏情况。

2.1 竖向位移分析

图8为5年后地层最终竖向位移结果。图8中位移正值表示隆起,位移负值表示沉降。从图8可以看出,最大沉降发生在渗气口(D1)位置两侧,其最大沉降值为26.0 mm。渗气口处的最终沉降位移约为10.5 mm。其沉降位移比两侧位移小的原因是渗气口下方由于气体快速流出产生的向上渗流力作用比两侧土体更大所导致。该点处沉降随时间变化的趋势如图9(a)所示。从图9(a)可以看出,渗流开始后渗气口的沉降位移迅速增大,而后产生少量回弹并逐渐稳定。图9(b)为图9(a)前期的局部放大。通过图9(b)可以看出,沉降发生的时间主要在前50 h内,后续产生少量回弹直至达到基本稳定。回弹产生的原因是由于含气地层的气体快速渗漏引起整个地层的初期沉降,而后随着地下水的涌入以及地层的卸荷效应产生回弹并逐渐达到平衡。

图8 最终竖向位移Fig.8 Final vertical displacement

图9 渗气口竖向位移随时间变化Fig.9 Distribution of the vertical displacement with time at the gas permeation port

图10(a)、图10(b)分别为隧道上部和下部观察点的竖向位移随时间的变化。其中,隧道上部的沉降主要发生在渗气开始后的前50 h内,而后产生少量回弹直到稳定。在前50 h内,位于隧道顶部的观察点(U3)沉降最大,而后3个观察点均有所回弹；最终隧道上部所有观察点的沉降稳定值相差较小,隧道顶部的观察点(U3)沉降最大,最大值约为12.3 mm。而隧道下部的观察点(D2～D5)的竖向位移开始有所波动,而后均有所回弹；其中位于含气层底部的点回弹值最大,达到了15 mm。越接近含气地层底部,回弹越明显。引起回弹的原因可能是含气地层下部的部分地层的卸荷效应。

图10 观察点竖向位移随时间变化Fig.10 Distribution of the vertical displacement with time at the observation points

图11为隧道中部(y=0)截面地表的沉降位移曲线。从图11可以看出，地表沉降位移曲线呈漏斗状,位于渗气点正上方的地表点沉降最大,向两侧逐渐减小，其最大沉降为7.5 mm。

图11 地表竖向位移曲线分布Fig.11 Distribution of the surface vertical displacement

2.2 截面附加弯矩分析

图12为隧道中部(y=0)截面最终附加弯矩。截面附加弯矩是由排气引起的弯矩。由图12可知,渗气口的位置两侧,截面附加弯矩最大,附加弯矩的最大值为41.7 kN·m/m；而越远离含气层的位置,截面附加弯矩越小。

根据苏通GIL工程盾构隧道的结构设计文件,隧道截面弯矩的设计值为1 708.1 kN·m/m,因此可知附加弯矩的最大值仅占设计值的2.4%。因此,可以认为含气地层的沉降对衬砌结构的受力影响较小。

2.3 饱和度与气压分析

最终饱和度分布如图13所示。从图13可以看出,整体含气层饱和度最小值为0.97。渗气口单元的饱和度随时间变化如图14所示,图14(b)为图14(a)前期的局部放大。从图14可以看出,饱和度逐渐增大到0.98。前期饱和度快速增加的原因是由于气体的迅速排出,土体饱和度增大,气压迅速下降,水压随之上升,导致基质吸力减小。

图13 最终饱和度分布Fig.13 Distribution of final saturation

图14 渗气口饱和度随时间的变化Fig.14 Distribution of saturation with time at the gas permeation port

渗气口及附近单元气压随时间变化如图15所示,图15(b)为图15(a)前期的局部放大图。从图15可以看出,所有观察单元的渗气压力都在初期迅速下降,而后缓慢下降直到稳定。其中,渗气口单元(E1)的最终气压为436 kPa,与该单元静水压(450 kPa)相差较小；而渗气口下方单元(E2、E3)的最终气压稳定在500 kPa左右，且深度越深,最终气压值也越大。

图15 渗气口及附近单元气压随时间的变化Fig.15 Distribution of gas pressure with time at the gas permeation port and nearby elements

3 结论

以苏通GIL综合管廊项目中盾构隧道穿越的长江江底浅层气体分布区为研究对象,采用自主开发的水-土-气三相渗流-变形耦合有限元程序,并基于文献[13-14]提出的本构模型模拟了含浅层沼气地层的变形特性,研究了气体渗流引起的地层不均匀沉降及其对隧道结构受力的影响,得出如下结论。

(1)根据位移计算结果,最大沉降发生在渗气口位置两侧,约为26.0 mm。隧道上部土体的沉降值先增大后由于回弹而有所减小,且越靠近隧道结构的土体的最终沉降值越大；隧道下部土体的沉降值整体上先随时间缓慢增大后产生回弹,且越接近含气地层底部边界的点回弹越大。而地表越靠近中心位置(渗气口上方),对应的竖向沉降位移值越大,整体呈漏斗状。

(2)根据截面附加弯矩的计算结果,渗气口两侧的截面附加弯矩最大,而越远离含气层的位置,截面附加弯矩越小。附加弯矩的最大值为41.7 kN·m/m,仅占设计值的2.4%。因此,含气地层的沉降对隧道结构的受力影响较小。

根据饱和度和气压变化的计算结果,气体渗漏过程完成后,含气层接近饱和。其中,渗气口前期饱和度快速增加的原因是由于气体的快速排出,土体饱和度上升,气压迅速下降,水压随之上升,导致基质吸力减小。渗气口最终饱和度为0.98,最终气压与该处静水压相差较小。

受限于目前的勘查技术水平,仅针对气体连续分布的典型气藏模型条件下的隧道变形受力情况进行了分析,然而实际地层中的气藏由于河流沉积作用或是松散堆积物的孔隙不同等原因并非单一均匀分布,其大小、位置以及形状都有很大的不确定性。为了更准确地模拟渗流场的变化过程,一种方法是建立精细化的气藏地质模型,这有赖于对土层和气藏信息的精细勘探技术；另一种方法是采用随机生成的地质模型描述分散分布的气藏,这将是笔者进一步探讨和研究的方向。