基于犹豫模糊语言下考虑后悔行为的双边匹配方法
彭欢欢,李 鹏*,陈胜男
(1.江苏科技大学 经济管理学院, 镇江212100) (2.黄河交通学院 经济管理学院, 焦作 454002)
双边匹配问题广泛地存在社会经济活动中,例如现实中最为熟知的婚姻匹配问题[1]、高校招生中学校与学生入学问题[2]、企业中员工与岗位的匹配问题[3-4]、买方与卖方达成匹配问题[5]、在双边交易市场中的供应商与顾客的匹配问题[6]、金融市场中风险投资商与企业的匹配问题[7-8]等.文献[9]将双边匹配方法应用到产业技术创新联盟合作对象的选择上;文献[10]通过建立双边主体的匹配度矩阵,构建优化模型来选择产学研合作伙伴.由此可见,双边匹配问题的研究具有广泛的实际应用价值和现实意义.
双边匹配研究两个互不相交集合中的不可分对象进行相互匹配的问题,最早用于学生入学和男女婚姻匹配的研究[1,11].传统的双边匹配方法以实数作为偏好信息,随后相继提出了关于语言数[12-13]、模糊数[14-15]、区间数[16]的模型.目前以犹豫模糊语言作为决策者偏好信息的双边匹配模型的研究较少,文献[17]提出犹豫模糊语言集,有效地刻画出人们在决策时犹豫不决的情形.近年来,有关犹豫模糊语言决策方法取得了大量的研究成果,文献[18]定义了决策矩阵间的共识性水平,建立犹豫模糊语言共识性调整模型;文献[19]对犹豫模糊语言的相关概念和特点进行分类;文献[20]提出一种更为合理的犹豫模糊语言的得分函数,并将其扩展到不平衡的犹豫模糊语言环境中;文献[21]构建基于犹豫模糊语言的一种优序关系模型;文献[22]定义犹豫模糊语言的集结算子, 并通过构建可能度公式比较其大小;文献[23]将灰集与犹豫模糊集相结合,构建一种新的灰色犹豫模糊集合.
在实际的决策过程中,双边匹配主体通常都是有限理性的.文献[24]将前景理论应用到双边匹配问题的研究中,考虑了双边主体的前景值,提出一种基于累积前景理论的双边匹配方法;文献[25]研究不确定偏好序信息下基于失望理论的双边匹配决策方法;文献[26]基于匹配主体的心理期望与感知,提出一种多属性双边匹配决策方法;文献[27]研究基于失望理论的双边主体心理的稳定双边匹配问题.
在已有的研究中,很少将后悔理论运用到双边匹配方法中.后悔理论的基本思想为:决策者在决策过程中,将当前所选择的方案与选择其他方案进行比较,如果当前选择的方案结果优于选择其他方案,则决策者内心感到欣喜,反之,则为后悔;在现实决策背景下,决策者总是选择后悔规避文献[28-29].该理论充分考虑双边匹配主体在决策过程中产生的后悔规避心理,使得决策过程更加合理科学.文献[30]将后悔理论与VIKOR方法相结合用于解决不确定多属性决策问题;文献[31]基于决策者有限理性的特点,将后悔理论运用到风险投资问题;文献[32]将后悔理论与区间灰数相结合并应用到突发事件应急决策问题.
文中构建一种基于犹豫模糊语言偏好信息的双边匹配模型,同时考虑到决策者的有限理性,将后悔理论运用到双边匹配问题的研究中,进而提出一种基于犹豫模糊语言下考虑决策者后悔行为的双边匹配方法.
1 预备知识
1.1 犹豫模糊语言术语
定义1[33]设τ为一正实数,则语言术语集可表示为S={si|i=0,1,…,2τ},且满足以下条件:
(1) 若α<β,则sα (2) 若nge(sα)=sβ,则α+β=2τ; (3) 若min(sα,sβ)=sα,则max(sα,sβ)=sα; (4) 若sα≤sβ,则min(sα,sβ)=sα. (1)sα⊗sβ=sβ⊗sα; (2) (sβ)λ=sβλ; (3) (sα⊗sβ)λ=(sα)λ⊗(sβ)λ; (4) (λ1+λ2)sα=λ1sα⊕λ2sα. 定义2[35]设S={si|i=0,1,…,2τ}为语言术语集,则称S中的有序连续语言术语组成的集合HS为S上的犹豫模糊语言术语集(HFLTS). hs(xi)={sφl(xi)|sφl(xi)∈S,l=1,2,…,L},其中,hs(xi)为S中元素构成的集合,称为犹豫模糊语言元素(HFLE),L为hs(xi)中元素的个数. (1) (2) 后悔理论考虑了决策者的后悔和欣喜两种心理状态,决策者选择方案的感知效用由两部分组成:效用函数v(x)和后悔-欣喜函数R(Δv),其中Δv是决策者选择该方案与最佳方案相比较带来的效用值之差.R(Δv)>0时,表示该方案决策者是欣喜的;R(Δv)<0时,表示该方案让决策者感到后悔.设决策者有A和B两个备选方案,x和y分别是对应的决策信息,则方案A的感知效用可以表达为: u(x)=v(x)+R[v(x)-v(y)] (3) 1.2.1 效用函数 在犹豫模糊语言信息背景下的决策问题,考虑到决策者后悔规避的心理,针对属性为效率型,效用函数计算公式为: (4) 效用函数v(x)是单调递增的凹函数[25],其中v(x)′>0,v(x)″<0;α是决策者的风险规避系数,且α的大小与决策者风险规避程度呈正相关关系. 对于成本型属性,v(x)是单调递减的凹函数,满足v(x)′<0,v(x)″<0.故效用函数计算公式为: v(x)=1-exp(βx) (5) 式中:β为决策者的风险规避系数,β∈(0,1),且β取值越大表示决策者风险规避的程度越大. 1.2.2 后悔-欣喜函数 通常情况下,决策者在面对双边匹配问题时,总是存在寻求后悔规避的心理行为,因此后悔-欣喜函数R(Δv)是单调递增的凹函数[28,38].计算公式为: R(Δv)=1-exp(-γΔv) (6) 式中:Δv是两个方案的效用差的变量,若R(Δv)<0表示后悔值;反之则为欣喜值. 对于双边匹配问题,设甲方主体集合为A={A1,A2,…,Am},其中Ai为甲方中第i个主体,i=1,2,…,m,m≥2;乙方主体集合为B={B1,B2,…,Bn},其中Bj为乙方中第j个主体,j=1,2,…,n,n≥2;不妨假设m≤n,M={1,2,…,m},N={1,2,…,n}. 定义5[39]设μ:A∪B→A∪B为一一映射关系,对于任意的Ai∈A,任意的Bj∈B,并且满足: (1)μ(Ai)∈B (2)μ(Bj)∈A∩{Bj} (3)μ(Ai)=Bj,当且仅当μ(Bj)=Ai 则称μ是双边匹配.μ(Ai)=Bj代表Ai与Bj在μ实现匹配,此时Ai和Bj都被称为匹配主体,若不符合上述条件,则表示匹配失败. 考虑解决的问题是双边主体一方集合A中主体和另一方集合B中主体分别依据相对应的指标,通过犹豫模糊语言来表征双边主体的不确定性偏好信息.同时考虑双边主体在决策过程中的有限理性,将后悔理论纳入决策过程中,通过建立双边匹配的优化模型,实现双边主体一方集合A中的主体与另一方集合B中的主体形成一一匹配. 在双边匹配的决策问题中,设甲方主体集合为A={A1,A2,…,Am},其中Ai为甲方中第i个主体,i=1,2,…,m,m≥2;乙方主体集合为B={B1,B2,…,Bn},其中Bj为乙方中第j个主体,j=1,2,…,n,n≥2.甲方主体A集合针对属性cj,用Dij(w)表示方案Pi与其他方案的离差,则可以定义为: 构造拉格朗日辅助函数可得: (7) 对wj,λ进行求偏导,同时令 进一步求解该模型,并进行归一化处理得到属性权重的计算公式为: (8) 同理乙方主体B集合针对属性c′j,用Dij(w)′表示方案P′i与其他方案的离差,则可以定义为 则Dj(w)′表示对于属性cj来说,所有方案与其他方案的离差总和,基于离差最大化的思想得: 进一步求解该模型,并进行归一化处理得到属性权重的计算公式为: (9) (10) (11) (12) (13) 根据式(8)可以计算出甲方主体A集合对于每个方案的综合感知效用为: (14) (15) 设xij为0-1变量,其中xij=1表示双边主体甲方Ai和乙方Bj匹配成功;xij=0则表示匹配主体Ai与另一方匹配主体Bj未达成匹配.以双方主体的感知效用最大化为决策目标,建立双边主体的多目标优化模型为: (16) (17) (18) (19) xij∈{0,1},i∈M,j∈N (20) 式(16)为主体甲方对乙方最大化的感知效用,式(17)为主体乙方对甲方最大化的感知效用;式(18)为甲方Ai中最多只能与乙方Bj中的一个主体相匹配或者不匹配;式(19)为乙方Bj中至多与甲方Ai中的一个主体相匹配或者不匹配;式(20)为xij只能取1或者0. 在式(16~20)中,由于匹配双方目标函数的量纲量级是相同的,故通过采用线性加权的方法,将多目标函数转化为单目标函数进行最终的求解.其中wA和wB分别为双边主体A和B的权重,且wA+wB=1,权匹配主体的重要程度是通过权重的大小来反映的,匹配主体一方占据主导地位则相应的权重就高一些.案例中的高校和企业两个主体占据同等地位,取wA=wB=0.5. (21) (22) (23) xij∈{0,1},i∈M,j∈N (24) 综上所述,基于犹豫模糊语言背景下考虑后悔行为的双边匹配方法计算步骤如下: Step1 依据式(1)将双边主体给出的犹豫模糊语言偏好信息通过得分函数转化为得分矩阵; Step2 依据匹配双方的得分矩阵,根据式(4)计算双边主体在不同属性状态下的效用值,得到双边主体的效用函数值; Step3 依据式(10~11)分别计算双边主体的后悔矩阵,再依据式(12~13)得到双边主体的感知效用矩阵; Step4 依据式(2,8,9)运用离差最大化分别计算双边主体在各指标下的权重,根据式(8,9)进行集结得到双边主体的综合感知效用矩阵; Step5 构建双边匹配模型(16~20),利用线性加权的方法构建单目标规划模型(21~24); Step6 通过利用LINGO11.0求解模型(21~24),得到双边匹配方案. 智能制造装备联盟内有16家会员单位,依据校企合作需求,经过筛选得到5所高校分别是清华大学A1,北京航空航天大学A2、华中科技大学A3、西安交通大学A4和同济大学A5;6家企业分别是上海克来机电自动化工程股份有限公司B1、安徽合力股份有限公司B2、大连智云自动化装备股份有限责任公B3、南京埃斯顿自动化股份有限公司B4、华中数控股份有限公司B5和浙江田中精机股份有限公司B6进入了最终的项目分工合作对接.由此组成高校主体集合A={A1,A2,A3,A4,A5};企业主体B={B1,B2,B3,B4,B5,B6},其中Ai表示第i个高校,i∈{1,2,3,4,5},Bj表示第j个企业,j∈{1,2,3,4,5,6};语言术语集表示为S={S0=极差,S1=很差,S2=差,S3=一般,S4=好,S5=很好,S6=极好}. 高校专家选取了4项指标(企业的科研人才水平D1、企业的数字化技术水平D2、相关科技产品收入D3(单位:万元)、机床制造技术水平D4)作为企业的评价标准.各高校通过犹豫模糊语言的形式给出对于各企业的偏好信息(表1).同时,企业根据专家建议采取科研人才队伍素质水平C1、飞行器设计与控制技术领先水平C2、科研产出水平C3、相关发明专利数C4(单位:个)4项指标作为高校的评价标准,各企业对高校给出了相应的偏好信息(表2). 表2 企业对于高校的偏好信息Table 2 Preference information of enterprises for universities 表1 高校对企业的偏好信息Table 1 Preference information of universities for enterprises 进而可以获得双边主体在不同属性状态下的感知效用(表3,4),其中选取参数α=β=0.88[38],γ=0.72. 表3 高校对企业的感知效用Table 3 Perceived utility of universities to enterprises 依据高校对企业给出的偏好信息,利用式(2,8)计算得到高校主体在不同属性状态下的权重分别为: w1=(0.199,0.186,0.373,0.242), w2=(0.185, 0.225, 0.325,0.265), w3= (0.224,0.259, 0.263,0.254), w4=(0.276,0.132,0.287,0.305), w5=(0.278, 0.196,0.263,0.263). 同理根据企业对高校给出的偏好信息,根据式(2,9)计算出企业主体在不同属性状态下的权重分别为: w′1=(0.122, 0.225,0.429,0.224), w′2=(0.295, 0.246, 0.246,0.213), w′3=(0.327, 0.091,0.291,0.291), w′4=(0.274, 0.239,0.258,0.229), w′5=(0.254,0.322,0.288, 0.136), w′6=(0.304,0.145,0.304, 0.247). 表4 企业对高校的感知效用Table 4 Perceived utility of enterprises to universities 利用公式(8,9)分别集结求得高校对企业的综合感知效用矩阵及企业对高校的综合感知效用矩阵,分别为: 建立双边匹配模型,利用线性加权的方法将多目标模型转化为单目标模型,使用LINGO11.0软件进行求解,得到最终结果: x12=x25=x36=x41=x54=1,其余的xij=0. 得到最终的双边匹配方案:高校A1和企业B2相匹配,高校A2和企业B5相匹配,高校A3和企业B6相匹配,高校A4和企业B1相匹配,高校A5和企业B4相匹配,企业B1没有和任何高校达成匹配. 针对以犹豫模糊语言刻画决策偏好信息的双边匹配问题,文中提出了一种基于后悔理论的双边匹配方法.犹豫模糊语言在表征决策信息的过程中,更能体现双边匹配主体在决策过程中的犹豫性和不确定性,更加贴合现实决策过程中人们的思维;同时考虑决策过程的非理性,将后悔理论引入双边匹配问题中,弥补了双边匹配忽略决策者有限理性的不足,使得决策更加符合实际.利用后悔理论构造双边匹配主体的感知效用,以双边主体感知效用最大化作为目标,建立双边匹配优化模型,利用线性加权的方法求解模型.文中构建的双边匹配模型与基于前景理论的双边匹配方法相比,涉及参数较少,计算过程不繁琐,因而具有很强的操作性,将其应用到产学研合作的案例中,为解决产学研合作过程中遇到的双边匹配问题提供了一种新的思路和途径. 参考文献(References) [1] GALE D, SHAPLEY L S. College admissions and the stability of marriage[J]. The American Mathematica Monthly, 1962, 69(1): 9-15.DOI:10.2307/2312726. [2] PAIS J. Random matching in the college admissions problem[J]. Economic Theory, 2007, 35(1): 99-116.DOI:10.2307/40282846. [3] GOODMAN S A, SVYANTEK D J. Person-organization fit and contextual performance: do shared values matter[J]. Journal of Vocational Behavior, 1999, 55(2): 254-275.DOI:10.1006/jvbe.1998.1682. [4] 陈希,樊治平.考虑多种形式信息的求职者与岗位双边匹配研究[J].运筹与管理, 2009,18(6): 103-109.DOI:10.3969/j.issn.1007-3221.2009.06.020. CHEN Xi, FAN Zhiping. Research on two-sided matching problem between employees and positions based on multiple format information [J]. Operations Research and Management, 2009, 18 (6): 103-109. DOI:10.3969/j.issn.1007-3221.2009.06.020. (in Chinese) [5] CHEN J, SONG K. Two-sided matching in the loan market[J]. International Journal of Industrial Organization, 2013, 31(2): 145-152.DOI:10.1016/j.ijindorg.2012.12.002. [6] XU Xinkai, WANG Chun, ZENG Yong, et al. Matching service providers and customers in two-sided dynamic markets[J]. IFAC-Papers OnLine, 2015, 48(3): 2208-2213.DOI:10.1016/j.ifacol.2015.06.416. [7] ELITZURR, GAVIOUS A. A multi-period game theoretic model of venture capitalists and entrepreneurs[J]. European Journal of Operational Research, 2003, 144(2): 440-453. [8] SQRENSEN M. How smart is smart money? A two-sided matching model of venture capital[J]. The Journal of Finance, 2007, 62(6): 2725-2762.DOI:10.1111/j.1540-6261.2007.01291.x. [9] 李锋, 喻志鹏, 冯瑶. 基于知识转移视角的产业技术创新联盟内部合作对象匹配研究[J]. 江苏科技大学学报(自然科学版), 2019,33(2):81-87.DOI:10.11917/j.issn.1673-4807.2019.02.014. LI Fu, YU Zhipeng, FENG Yao. Research on the cooperation partner matching of industrial technology innovation alliance based on knowledge transfer[J]. Journal of Jiangsu University of Science and Technology (Natural Science Edition), 2019, 33(2): 81-87.DOI:10.11917/j.issn.1673-4807.2019.02.014. (in Chinese) [10] 张裕稳, 吴洁, 李鹏, 等. 创新能力视角下基于双边匹配的产学研合作伙伴选择[J]. 江苏科技大学学报(自然科学版), 2015, 29(5): 488-495.DOI:10.3969/j.issn.1673-4807.2015.05.014. ZHANG Yuwen, WU Jie, LI Peng, et al. Partner selection of industry-university-research collaboration based on two-sided matching from the perspective of innovation capacity[J]. Journal of Jiangsu University of Science and Technology (Natural Science Edition), 2015, 29(5): 488-495.DOI:10.3969/j.issn.1673-4807.2015.05.014. (in Chinese) [11] ALKAN A, GALE D. Stable schedule matching under revealed preference[J]. Journal of Economic Theory, 2003, 112(2): 289-306.DOI:10.1016/S0022-0531(03)00096-6. [12] HUYNH V N, NAKAMORI Y. A satisfactory-oriented approach to multiexpert decision-making with linguistic assessments[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part B: Cybernetics, 2005, 35(2): 184-196.DOI:10.1109/TSMCB.2004.842248. [13] 陈希,樊治平.电子采购中具有语言评价信息的交易匹配问题研究[J].运筹与管理, 2009,18(3): 132-137.DOI:10.3969/j.issn.1007-3221.2009.03.024. CHEN Xin, FAN Zhiping. Research on trade matching problem in electronic procurement with linguistic assessment information [J]. Operations Research and Management Science, 2009, 18 (3): 132-137. DOI:10.3969/j.issn.1007-3221.2009.03.024. (in Chinese) [14] JIANG Z Z, FAN Z P, WANG D W. Trade matching for multi-attribute exchanges with fuzzy information and indivisible demand in E-brokerage[J]. Systems Engineering-Theory & Practice,2011, 31(12):2355-2366.DOI:10.1016/j.cnsns.2011.01.018. [15] JIANG Z Z, FAN Z P, WANG D W, et al. Matching model and algorithm for multi-unit multi-attribute exchanges with fuzzy information in E-brokerage[J]. Journal of Management Sciences in China, 2014,17(5):52-65. [16] 张笛, 孙涛,陈洪转,等.多种形式不确定偏好信息下考虑后悔行为的双边匹配方法[J]. 系统工程与电子技术, 2019, 41(1): 118-123.DOI:10.3969/j.issn.1001-506X.2019.01.17. ZHANG Di, SUN Tao, CHEN Hongzhuan, et al. Method for two-sided matching with multi-form uncertain preference information considering regret behavior [J]. Systems Engineering and Electronics, 2019, 41 (1): 118-123. DOI:10.3969/j.issn.1001-506X.2019.01.17. (in Chinese) [18] 魏翠萍, 马京. 犹豫模糊语言群决策的共识性模型[J]. 控制与决策, 2018, 33(2): 275-281.DOI:10.13195/j.kzyjc.2016.1665. WEI Cuiping, MA Jing. Consensus model for hesitant fuzzy linguistic group decision making [J]. Control and Decision, 2018, 33 (2): 275-281. DOI:10.13195/j.kzyjc.2016.1665. (in Chinese) [19] WANG Hai, XU Zeshui, ZENG Xiaojun. Hesitant fuzzy linguistic term sets for linguistic decision making: Current developments, issues and challenges[J]. Information Fusion, 2018, 43: 1-12.DOI:10.1016/j.inffus.2017.11.010. [20] LIAO Huchang, QIN Rui, GAO Chenyuan, et al. Score-HeDLiSF: A score function of hesitant fuzzy linguistic term set based on hesitant degrees and linguistic scale functions: An application to unbalanced hesitant fuzzy linguistic multimoora[J]. Information Fusion, 2019, 48:39-54.DOI:10.1016/j.inffus.2018.08.006. [21] 王坚强, 吴佳亭. 基于优序关系的犹豫模糊语言多准则决策方法[J].控制与决策,2015,30(5):887-891.DOI:10.13195/j.kzyjc.2014.0210. WANG Jianqiang, WU Jiating. Method for multi-criteria decision-making with hesitant fuzzy linguistic based on outranking relation [J]. Control and Decision, 2015, 30 (5): 887-891. DOI:10.13195/j.kzyjc.2014.0210. (in Chinese) [22] WEI Cuiping, ZHAO Na, TANG Xijin. Operators and comparisons of hesitant fuzzy linguistic term sets[J]. IEEE Trans on Fuzzy Systems, 2014, 22(3): 575-585.DOI:10.1109/TFUZZ.2013.2269144. [23] 李庆胜, 刘思峰. 灰色犹豫模糊集及其灰关联TOPSIS决策方法[J]. 江苏科技大学学报(自然科学版), 2015,29(6):597-601.DOI:10.3969/j.issn.1673-4807.2015.06.016. LI Qingsheng, LIU Sifeng. Grey hesitant fuzzy sets and its decision making based on grey relation and TOPSIS [J]. Journal of Jiangsu University of Science and Technology (Natural Science Edition), 2015, 29(6): 597-601. DOI:10.3969/j.issn.1673-4807.2015.06.016. (in Chinese) [24] 乐琦, 樊治平.基于累积前景理论的双边匹配决策方法[J].系统工程学报,2013,28(1):38-46.DOI:10.3969/j.issn.1000-5781.2013.01.005. LE Qi, FAN Zhiping. Decision method for two-sided matching based on cumulative prospect theory [J]. Journal of Systems Engineering, 2013, 28 (1): 38-46. DOI:10.3969/j.issn.1000-5781.2013.01.005. (in Chinese) [25] FAN Zhiping, LI Mingyang, ZHANG Xiao. Satisfied two side matching: A method considering elation and disappointment of agents [J]. Soft Computing, 2018, 22(1): 1-15.DOI:10.1007/s00500-017-2725-1. [26] 陈希,韩菁,张晓.考虑心理期望与感知的多属性匹配决策方法[J].控制与决策,2014,29(11):2027-2033.DOI:10.13195/j.kzyjc.2013.1272. CHEN Xi, HAN Jing, ZHANG Xiao. Method for multiple attribute matching decision making considering matching body′s psychological aspiration and perception [J]. Control and Decision, 2014 ,29(11): 2027-2033. DOI:10.13195/j.kzyjc.2013.1272. (in Chinese) [27] 李铭洋, 樊治平.考虑双方主体心理行为的稳定双边匹配方法[J].系统工程理论与实践,2014, 34(10): 2591-2599. LI Mingyang, FAN Zhiping. Method for stable two-sided matching considering psychological behavior of agents on both sides [J]. Systems Engineering-Theory & Practice, 2014, 34 (10): 2591-2599. (in Chinese) [28] LOOMES Q, SUGDEN R. Regret theory: An alternative of rational choice under uncertainty [J]. Economic Journal, 1982, 92(4): 805-824. [29] BELL D E. Regret indecision making under uncertainty [J]. Operations,1982, 30(5): 961-981. [30] 谭春桥,张晓丹. 基于后悔理论的不确定风险型多属性决策VIKOR方法[J].统计与决策, 2019, 35(1): 47-51.DOI:10.13546/j.cnki.tjyjc.2019.01.010. TAN Chunqiao, ZHANG Xiaodan. VIKOR method for uncertain risky multi-attribute decision making based on regret theory [J]. Statistics and Decision, 2019, 35 (1): 47-51. DOI:10.13546/j.cnki.tjyjc.2019.01.010. (in Chinese) [31] 于超,樊治平.考虑决策者后悔规避的风险投资项目选择方法[J].中国管理科学,2016,24(6): 29-37.DOI:10.16381/j.cnki.issn1003-207x.2016.06.004. YU Chao, FAN Zhiping. Method for venture capital project selection considering decision maker′s regret aversion [J]. Chinese Journal of Management Science, 2016, 24(6): 29-37. DOI:10.16381/j.cnki.issn1003-207x.2016.06.004. (in Chinese) [32] 钱丽丽, 刘思峰.考虑后悔行为的灰色应急决策方法[J].数学的实践与认识, 2019, 49 (5): 92-98. QIAN Lili, LIU Sifeng. Grey decision-making method for emergency response with regret aversion [J]. Mathematics in Practice and Theory, 2019, 49 (5): 92-98. (in Chinese) [33] RODRIGUEZ R M, MARTINEZ L, HERRERA F, et al. Hesitant fuzzy linguistic term sets for decision making[J]. IEEE Trans on Fuzzy Systems, 2012, 20(1): 109-119. [34] XU Zeshui. Deviation measures of linguistic preference relations in group decision making[J]. Omega, 2005, 33(3): 249-254.DOI:10.1016/j.omega.2004.04.008. [35] LIAO Huchang, XU Zeshui, ZENG Xiaojun. Distance and similarity measures for hesitant fuzzy linguistic term sets and their application in multi-criteria decision making[J]. Information Sciences, 2014, 271:125-142.DOI:10.1016/j.ins.2014.02.125. [36] WEI Cuiping, REN Zhiliang, RODRGUEZ R M. A hesitant fuzzy linguistic todim method based on a score function[J]. International Journal of Computational Intelligence Systems, 2015, 8(4):701-712. DOI:10.1080/18756891.2015.1046329. [37] LI Ping, WEI Cuiping. A case-based reasoning decision-making model for hesitant fuzzy linguistic information[J]. International Journal of Fuzzy Systems, 2018, 20(7): 2175-2186.DOI:10.1007/s40815-017-0391-1. [38] TVERSKY A, KAHNEMAN D. Advances in prospect theory: cumulative representation of uncertainty [J]. Journal of Risk and Uncertainty, 1992, 5(4):297-323.DOI:10.1007/bf00122574. [39] 乐琦, 樊治平.一种具有序值信息的双边匹配决策方法[J].系统工程学报, 2012, 27(2): 185-192. DOI:10.3969/j.issn.1000-5781.2012.02.006. LE Qi, FAN Zhiping. Method for two-sided matching decision-making with ordinal numbers[J].Journal of Systems Engineering, 2012, 27 (2): 185-192. DOI:10.3969/j.issn.1000-5781.2012.02.006. (in Chinese)
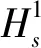

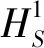

1.2 后悔理论
1.3 双边匹配基本理论
2 基于后悔理论的犹豫模糊语言双边匹配决策方法
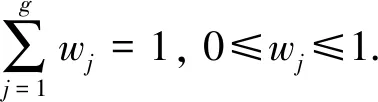
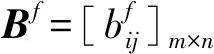
2.1 基于犹豫模糊语言的离差最大化定权方法
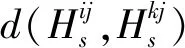


2.2 双边匹配决策模型的构建




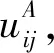


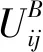
2.3 双边匹配决策模型的求解
2.4 双边匹配决策方法的步骤
3 算例分析
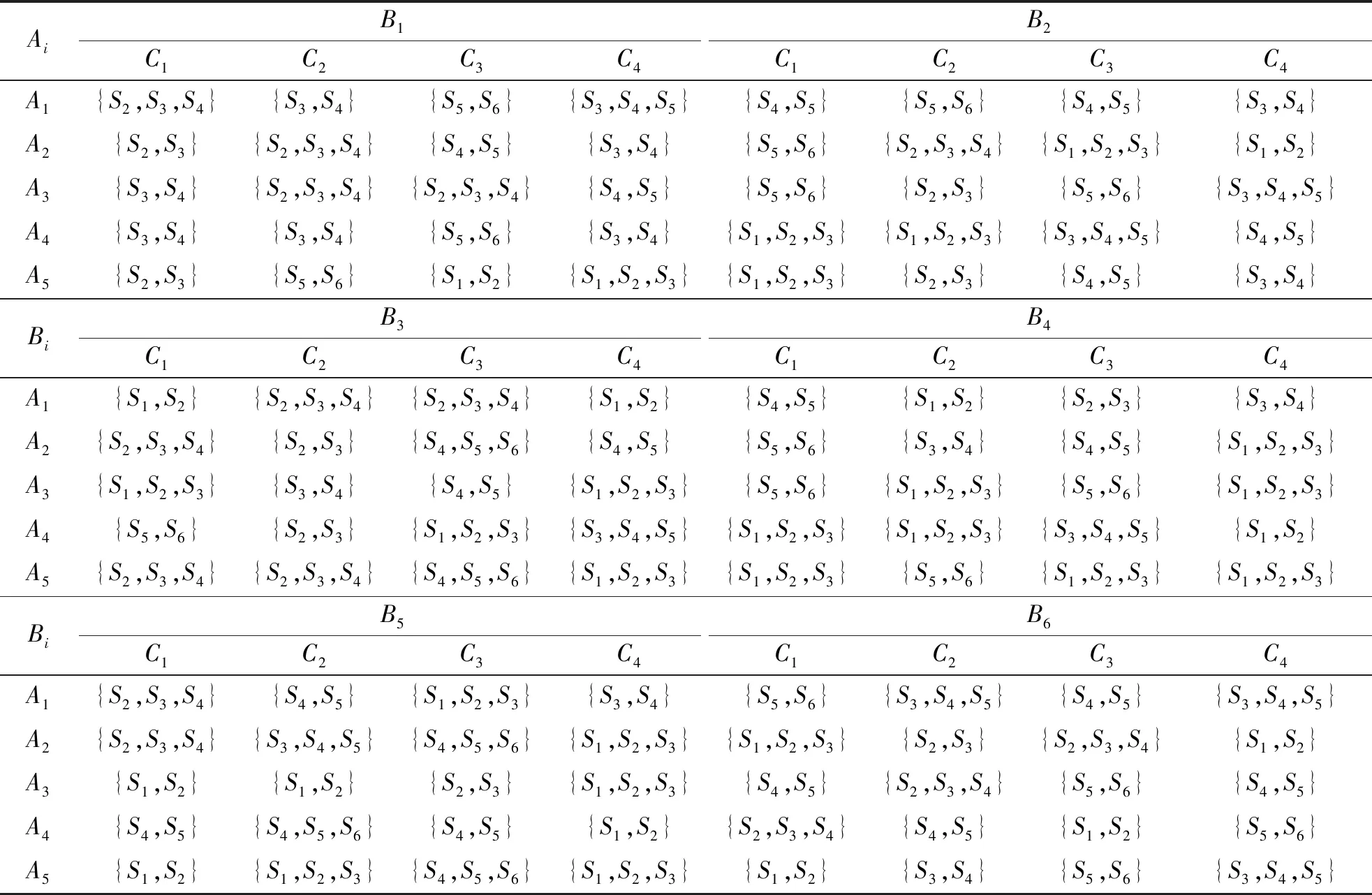



4 结论

