基于NSGA-II算法的编队卫星重构策略
孙鸿强,张占月,方宇强
(航天工程大学 研究生院,北京 101416)
航天器轨道优化对延长在轨寿命、降低风险系数、增大有效载荷以及保证工作效率等方面有着重要的实践价值.早在20世纪60年代,针对空间最优轨道机动问题就开展了大量的研究工作.在分析最优轨道方面,遗传算法、粒子群优化(PSO)算法和模拟退火算法[1-2]等为解决复杂问题提供了新的思路和手段.与此同时,空间环境愈发复杂,截至2019年8月,美国空间监视网编目了大于10 cm的空间目标约 23 000 个,对外公布已编目的在轨目标 19 524 个,其中 14 495 个为空间碎片[3-4].此外,美国太空探索技术公司宣称要将其Starlink项目的低轨卫星增至 42 000 颗.2019年9月2日,欧洲航天局表示为了避免与Starlink44卫星相撞,在预计碰撞前1 h内对Aeolus卫星进行了机动,利用卫星携带的推进器将轨道高度增加约350 m,从而将碰撞概率降到安全阈值以下.
在卫星规避机动方面,其方式为利用所携带的燃料由安装在不同方位的推进装置获得既定的速度冲量,进而改变卫星的运行状态.目前,单星规避技术已相对成熟,主要采用基于碰撞概率的单颗卫星规避机动方法.在获取空间目标的位置矢量、速度矢量以及位置误差协方差矩阵后,可对在轨航天器及其周围空间进行碰撞概率估算,以获得航天器周围空间的碰撞概率密度函数,进而确定最佳机动的大小和方向.
而对于编队卫星而言,由于卫星之间相互协作的特点,对其中的卫星进行机动将会引起整个编队工作效率的改变,若此时沿用单星预警规避机制,则无法同时兼顾机动消耗、碰撞概率、工作效率等指标,所以编队卫星如何在规避的同时兼顾上述多个指标的研究具有重要的价值和意义.针对当前卫星规避方面出现的问题,在文献[5]的基础上,采用并改进非支配排序遗传算法(NSGA-II),根据编队卫星的运行状态对其进行基因编码,以改进的差分进化(IDE)算法作为种群生成模型,以Pareto支配作为优劣评价标准,使得卫星在保证工作效率的情况下进行机动后不再恢复原构型.最后以海洋侦察卫星为例,将多个指标作为切入点制定规避策略.
1 数学模型
为了解编队卫星的规避质量,构建能量消耗、碰撞概率、工作效率等数学模型,并计算上述指标.
1.1 能量消耗模型
为尽可能减少消耗燃料,卫星进行规避机动之后,在保证工作效率的前提下将卫星驻留在规避终点,从而减少回归原轨道所消耗的燃料.在轨道规避的选择方面,国际上主要采用高度分离法(错开轨道高度)[6]和迹向分离法(错开轨道相位)[7].
同轨道相位调整主要分为相位超前调整和相位滞后调整[8],一般对于相位超前采用共面高轨变相,相位滞后则采用共面低轨变相[9].当相位需要调整时,需施加一迹向速度冲量,将航天器步入过渡轨道,缩短轨道周期,经若干个周期再次变轨回到原轨道,最终实现相位调整[10].由文献[5]可知,在近地轨道相位需要超前或滞后调整的情况下,单圈轨道机动所消耗的速度增量为
(1)
式中:Δvahe为相位超前时轨道机动所需的速度增量;Δvlag为相位滞后时轨道机动所需的速度增量;θ为相位角;RL为近地圆轨半径;μ为地球引力常数.
1.2 碰撞概率计算模型
根据观测站观测及国际公布的空间轨道数据对未来空间目标的运行轨道进行预推,计算其碰撞概率[11].美国国家航空航天局(NASA)将黄色碰撞预警值设定为10-5,红色碰撞预警值设定为10-4.
由于现有技术的局限性,对空间目标的轨道预报存在一定误差,该误差表现在在轨空间目标的迹向、径向和法向方向上,共同构成了一个误差椭球.当两个空间目标间的距离小于其等效半径之和时,可以判定为二者发生碰撞[12].在计算中,将联合体与误差椭球投影到相遇平面内可简化计算过程.
根据文献[11],碰撞概率的表达式可改写为
P=∬m2+n2≤R2f(m,n)dmdn=
(2)
式中:R为两个空间目标联合圆域的有效半径;m、n为相遇平面的两个坐标轴方向;d为两目标相对距离矢量;C为联合误差协方差矩阵.
计算碰撞概率的基本流程为获取接近信息,建立相关坐标系,构成联合误差椭球和联合体,在相遇坐标系中计算碰撞概率[12].
1.3 卫星定位效率计算模型
在卫星定位方面,到达时间差(TDOA)是广泛采用的技术.根据目标源的辐射信号到达不同卫星时间的不同,可利用几何关系进行定位求解[13].
假设f(α,β,γ)为地固坐标系下地球表面的简化表达形式,目标源在地固坐标系下的概略位置为S0(α0,β0,γ0),则将f(α,β,γ)在S0处展开可得:
(3)
式中:ΔS为Taylor展开后的高阶项.
利用地心至目标源的转换矩阵M可求得目标源当地坐标系的协方差矩阵ΔSloc,其表达式为
ΔSloc=MΔS
(4)
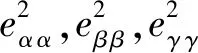
(5)
海洋侦察定位卫星的定位高度可视为0[15],因此仅进行水平方向的精度分析即可.假设目标源信号的传播时间测量均方差为σ0,电磁波传播速度为c,则此目标源的水平定位精度E可表示为
(6)
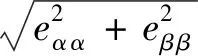
2 NSGA-II 算法的修正
NSGA-II 算法采用差分进化(DE)算法作为框架,结合Pareto支配的排序方法,对多目标优化问题进行求解,是一种适合对多目标函数进行优化的算法.针对NSGA-II 算法中差分进化阶段收敛速度较慢这一问题,提出一种基于判别函数的自适应算法,用于改进差分进化阶段的变异环节,在保证全局最优的情况下加快寻优速度.
2.1 差分进化算法
差分进化算法基本沿用遗传算法的框架,但是其在选择、交叉、变异等方面有着较大的差异,为之进行的操作也更为复杂.算法的实现步骤如下.
(1) 种群初始化
对于求解问题,需要给定种群数量、个体维数、每个维度的上下界,利用随机程序生成初始种群.初始随机种群可表示为
zj,i(0)=random(0,1)(bu-bl)+bl
(7)
j=1,2,…,D;i=1,2,…,NP
式中:zj,i(0)为初始代第i个个体上的第j个基因;random(0,1)为在(0,1)上均匀分布的随机数;NP为种群数量;D为个体维度;bu和bl为不同维度的上下界阈值.
(2) 变异操作
通过差分法实现变异需要给定进化代数和差分缩放因子,差分法利用变异概率PM随机选择种群中的两个个体,利用缩放因子将其差值进行缩放后与待变异个体进行合成,生成新的变异个体.变异操作可表示为
wi(G+1)=z1(G)+s[z2(G)-z3(G)]
(8)
式中:wi(G+1)为第(G+1)代第i个个体的变异个体;s为差分缩放因子;z1(G)、z2(G)、z3(G)分别为第G代的不同个体.由此,可通过上述方法生成变异个体.
(3) 交叉操作
交叉的对象为由上述步骤生成的所有个体,其中包括个体zi(G)和变异生成的个体wi(G+1),需要给定交叉概率以生成新的交叉个体.此外,为保证由变异新生成的基因得以延续,随机选择变异个体wi(G+1)中的第jran个基因作为等位基因遗传给交叉生成的个体,这样就保证了变异个体中至少有一个基因会遗传给下一代,保留了变异的合理性.交叉操作可表示为
uj,i(G+1)=
(9)
式中:uj,i(G+1)为第(G+1)代交叉生成的第i个个体上的第j个基因;PC为交叉概率;jran为[1,D]之间随机生成的正整数.交叉操作可以分为指数交叉和二项交叉[17].
(4) 选择操作
在完成上述步骤后,基于贪婪算法对种群个体进行选择,筛选出优质基因进入下一代种群.选择操作可表示为
zj,i(G+1)=
(10)
式中:F(·)为目标函数.根据贪婪算法对新生成的个体和初始个体进行比较,保留更适合目标函数的个体.
(5) 终止操作
当个体满足目标函数所设定的条件或进化代数G达到设定的最大代数Gmax时,停止进化操作;否则返回步骤(2)~(4)继续进行变异、交叉和选择操作,直至满足目标函数的设定.
2.2 差分进化的改进
由2.1节可知,差分进化算法的变异环节对待变异个体无要求,任何处于种群中的个体均可通过变异操作生成新的变异个体.变异操作的受众面广泛,更利于寻找全局最优解.但由于该过程中每个个体都可能成为待变异的个体,计算过程较为繁琐冗杂.此外,对于不符合设定期望的个体仍然进行变异操作也会造成计算空间的浪费.由此,文献[18]提出一种优质变异的进化算法,其思路为在变异过程中,选择种群中的优质个体作为待变异个体,对其进行变异操作,其表达式为
wi(G+1)=zbes(G)+s[z2(G)-z3(G)]
(11)
式中:zbes(G)为G代种群中符合设定函数期望的优质个体.由式(11)可知,该方法筛选了符合设定函数期望的优质个体集合,集合中的个体作为待变异个体,对其进行变异操作生成新的下一代个体.此方法降低了计算量,可以快速获得设定函数的最优解.但其亦存在一定的弊端,由于在筛选后舍去了一部分个体,所以在变异操作后,新生成的个体变化范围将会有所减少,不利于种群的多样性,容易陷入局部最优解,进而可能错失了求取全局最优解的机会.
结合上述两种差分进化算法,为尽可能快速地求得全局最优解,引入变异判别函数,对变异操作进行修正,以待变异个体的优质性为依据,采用不同的数学模型进行变异操作.该过程可表示为
wi(G+1)=
(12)
式中:Q(G)为变异判别函数.利用变异判别函数可对变异情况进行分类:① 在进化早期,由初始化生成的种群数量有限,有许多基因没有体现在种群个体之中,此时采用第1种随机选取待变异个体的进化方式,以保证种群的多样性,有利于寻求全局最优解;② 在进化晚期,经过筛选后种群内个体的基因趋于稳定,采用第2种选取优质个体作为待变异个体的进化方式,可以有效地减少冗余计算,获得优化结果.以下对判别函数Q(G)的选择进行分析讨论.
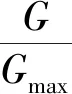
(13)
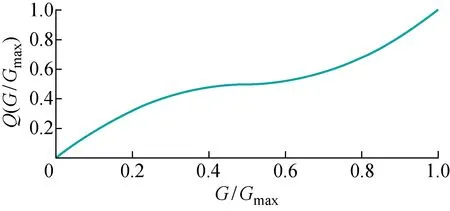
图1 变异判别函数Fig.1 Mutation discriminant function
wi(G+1)=
(14)
2.3 仿真算例
已知目标函数表达式如下,解向量T包含10个基因t1~t10,求目标函数在|ti|≤3内的最小值.
(15)
T=[t1t2…t10], |ti|≤3
参数设定为Gmax=5 000,PM=0.5,PC=0.9,D=10,NP=100.
利用所提改进的差分进化算法模型,经过种群初始化、变异操作、交叉操作和选择操作后,输出的优化结果如表1所示.
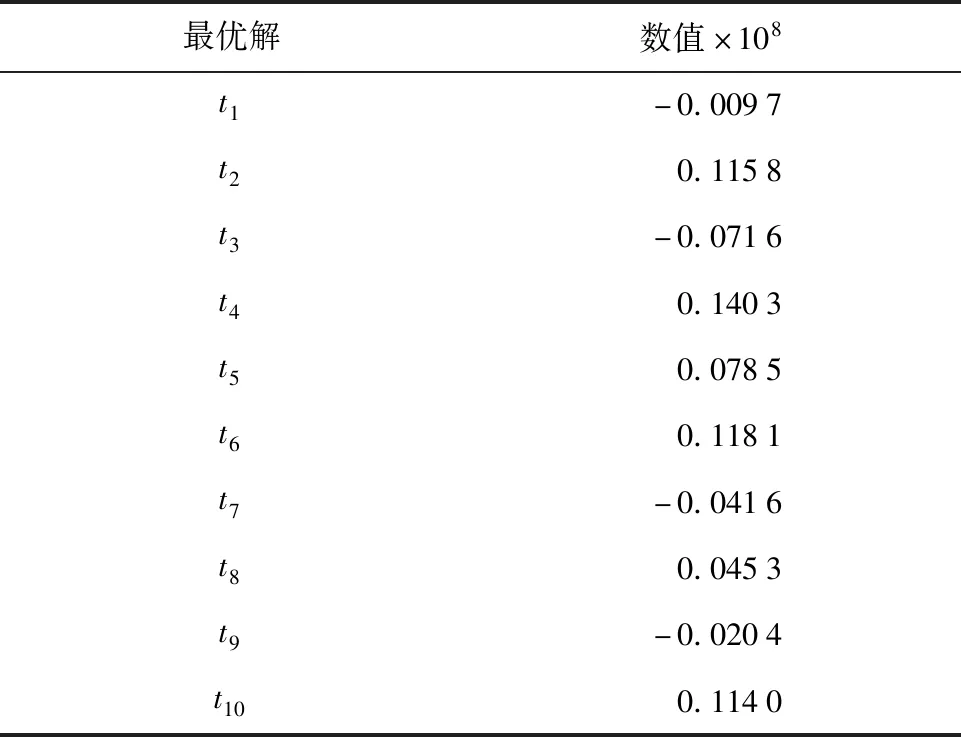
表1 目标函数最优解Tab.1 Optimal solution of objective function
将改进的差分进化算法与标准差分进化算法的计算过程进行比较,如图2所示.
由图2可以看出,在种群初始化时,两种方法初代解的最小值均远远大于全局最优解F(T)=0.随着种群不断进化,改进的差分进化算法的寻优速度更快,更早获得全局最优解,计算效率也更高.
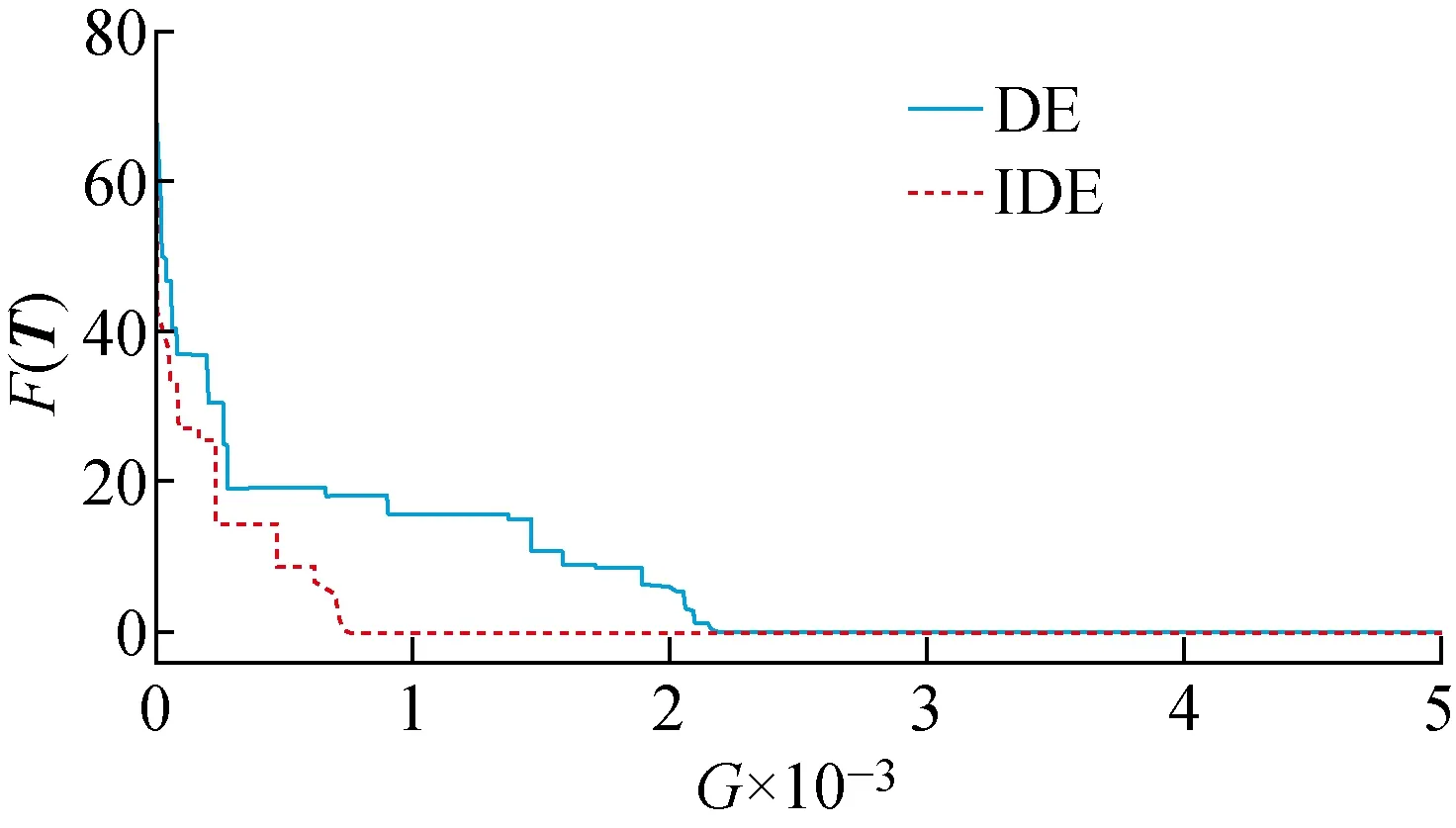
图2 IDE算法与DE算法比较Fig.2 Comparison of IDE algorithm and DE algorithm
3 NSGA-II算法在编队卫星上的应用
自然界的生物依靠基因的交叉、变异,不断进化达到更适合物种生存的状态,这一现象属于多目标优化问题[19-20].将编队卫星视为种群个体,每个个体均携带决定卫星参数的基因,利用NSGA-II 算法进行优化,最终获得最优解集[21].
3.1 基于编队卫星的编码方式
以三星编队的海洋监视卫星为例,在卫星躲避碎片而位置发生变化后,多个状态指标也随即发生改变,需要重点关注的指标有:卫星机动后的碰撞概率、卫星机动的能耗、编队卫星机动后的工作效率等.由此,可将目标函数设定为如下形式:
F(X)=F(P,W,η)
(16)
式中:W为卫星机动的能量消耗;η为编队卫星机动后的工作效率.
编队中卫星的机动位置主要依据轨道六根数进行确定.假设机动前后轨道均为近地圆轨,则沿迹分离机动时,轨道六根数中产生变化的是卫星的轨道半长轴a和真近点角f.因此,共轨道面上的卫星位置可由(a,f)表示.
采用3层基因编码对其进行描述.
(1) 上层基因zup,i决定该方案中有哪些卫星需进行规避机动,同时根据预警时间的长短选择合适的机动方式,可表示为
(17)
i=1,2,…,NP
由式(17)可知,上层基因可以决定编队卫星是否需要进行规避.当卫星需要机动时,可采用2.1节的沿迹分离轨道机动方式进行规避机动.上层基因起到了统筹全局、把握规避整体方向的作用.
(2) 中层基因zmid,i=(ai,fi)决定该卫星进行规避机动后的轨道半长轴和真近点角变化位置,可表示为
(18)
i=1,2,…,NP
式中:Δa为轨道半长轴的改变量;Δf为真近点角的改变量;种群数量NP=n.由于分析对象为近地圆轨,在同轨道面内,可由包含轨道半长轴和真近点角的中层基因对编队卫星在空间中的位置进行简化表达.此外,可根据中层基因对编队卫星的状态进行计算,如:根据坐标转化求出编队卫星在J2000坐标系下的位置和速度,根据这些信息进而可求得下层基因性状.故中层基因是最重要的部分,起到了承接上层基因,引导下层基因的作用.
(3) 下层基因包括卫星的碰撞概率、编队卫星的工作效率、卫星重构所需能量等由上、中层基因支配的变量,可表示为zlow,i=(Pi,Wi,ηi).其中,卫星的碰撞概率包括编队中的每颗卫星与空间碎片之间的碰撞概率,以及编队卫星之间的碰撞概率.在所研究的海洋监视卫星中,其主要需求为对海上目标的侦察定位,故可采用HDOP这一指标对工作效率进行描述.此外,编队卫星重构能量亦是需要考虑的方面,将每个进行机动操作的卫星能量消耗累加,获得总重构能量.下层基因的作用是对最关心的指标进行计算罗列,以便进行基因的优化筛选操作.综上,整个基因排列如图3所示.
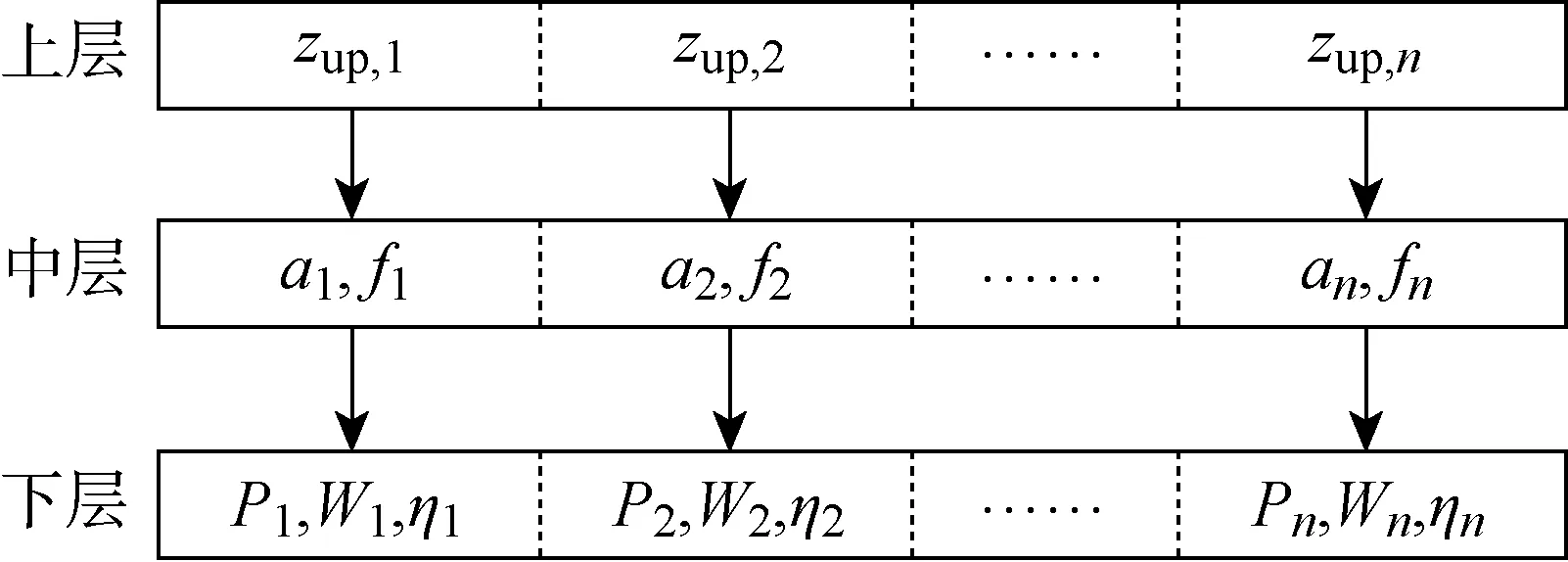
图3 上中下层基因编码示意图Fig.3 Diagram of upper,middle and lower level codes for genes
由上述步骤对卫星的机动位置进行基因编码,当对这些基因进行初始化、交叉、突变、查重等操作后,可以产生大量的描述不同编队卫星状态的基因以供筛选[22-23].
3.2 基于编队卫星的差分进化
由3.1节基因的定义可知,中层基因是最重要的组成部分,在对上层基因进行了详细表达的同时,也可根据中层基因对下层基因的组成进行计算,故在差分进化时选择中层基因作为差分进化的变量.
(1) 种群初始化
采用随机程序初始化编队卫星种群,以保证种群基因的全面性.由于中层基因包含轨道半长轴以及真近点角两个分量,所以将其维度设为2.此外,在初始化阶段需要对基因在不同维度上的边界进行限制.针对在轨卫星的碎片规避决策,其主要目标为躲避碎片的威胁,并不需要大幅度地调整卫星的位置,故在中层基因中,轨道半长轴设定的维度上下界为[-1,+1] km,在真近点角设定维度的上下界为[-0.5°,+0.5°],如图4所示.其中,五角星位置代表卫星所在位置.
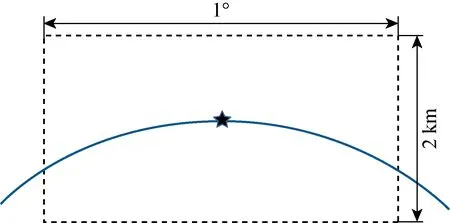
图4 编队卫星中层基因边界示意图Fig.4 Diagram of middle level gene boundary of formation satellites
(2) 变异操作
变异维度为2,故需要对轨道半长轴和真近点角分别进行变异操作,根据种群数量NP和变异概率PM确定进行变异的数量NM,NM=NP×PM.由2.2节分析,采用基于判别函数的自适应变异算法,对种群的中层基因进行变异.种群个体可依据其轨道半长轴和真近点角在二维坐标系下表示,如图5所示.
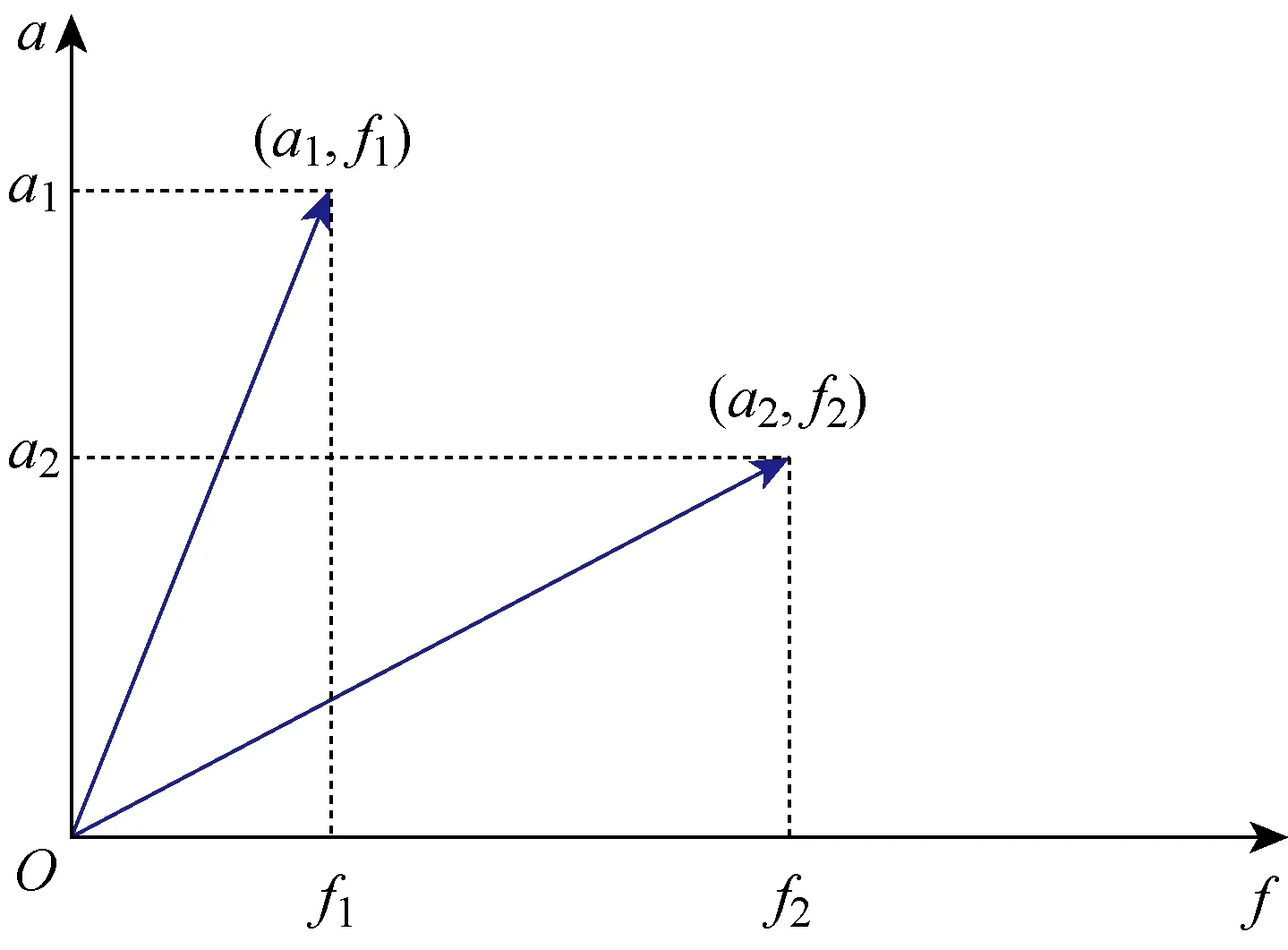
图5 种群个体在二维坐标系中的表示Fig.5 Individual populations in two-dimensional coordinates
为避免出现“早熟”现象,过早获得局部最优解进而影响整体最优的筛选,引入式(14)作为变异判别函数,对变异操作进行修正.为丰富种群的基因池,寻找全局最优解,在变异初期不对待变异个体进行要求,即随机选择待变异个体,对其进行变异操作;经过变异前期的积累,种群中基因的多样性得到增加,为加快寻优速度,在变异后期选取种群中的优质基因作为待变异个体.两种变异模式如图6和7所示.其中:aM为变异生成新个体w的轨道半长轴;fM为变异生成新个体w的真近点角;zmid,bes为中层优质基因.
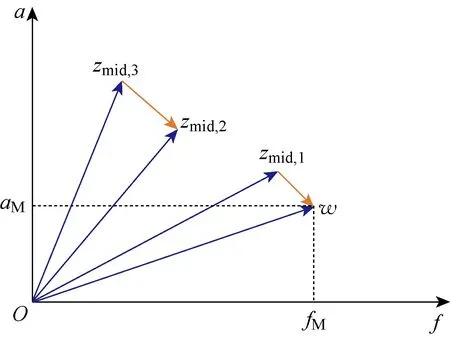
图6 初期变异操作模式Fig.6 Initial mutation operation mode
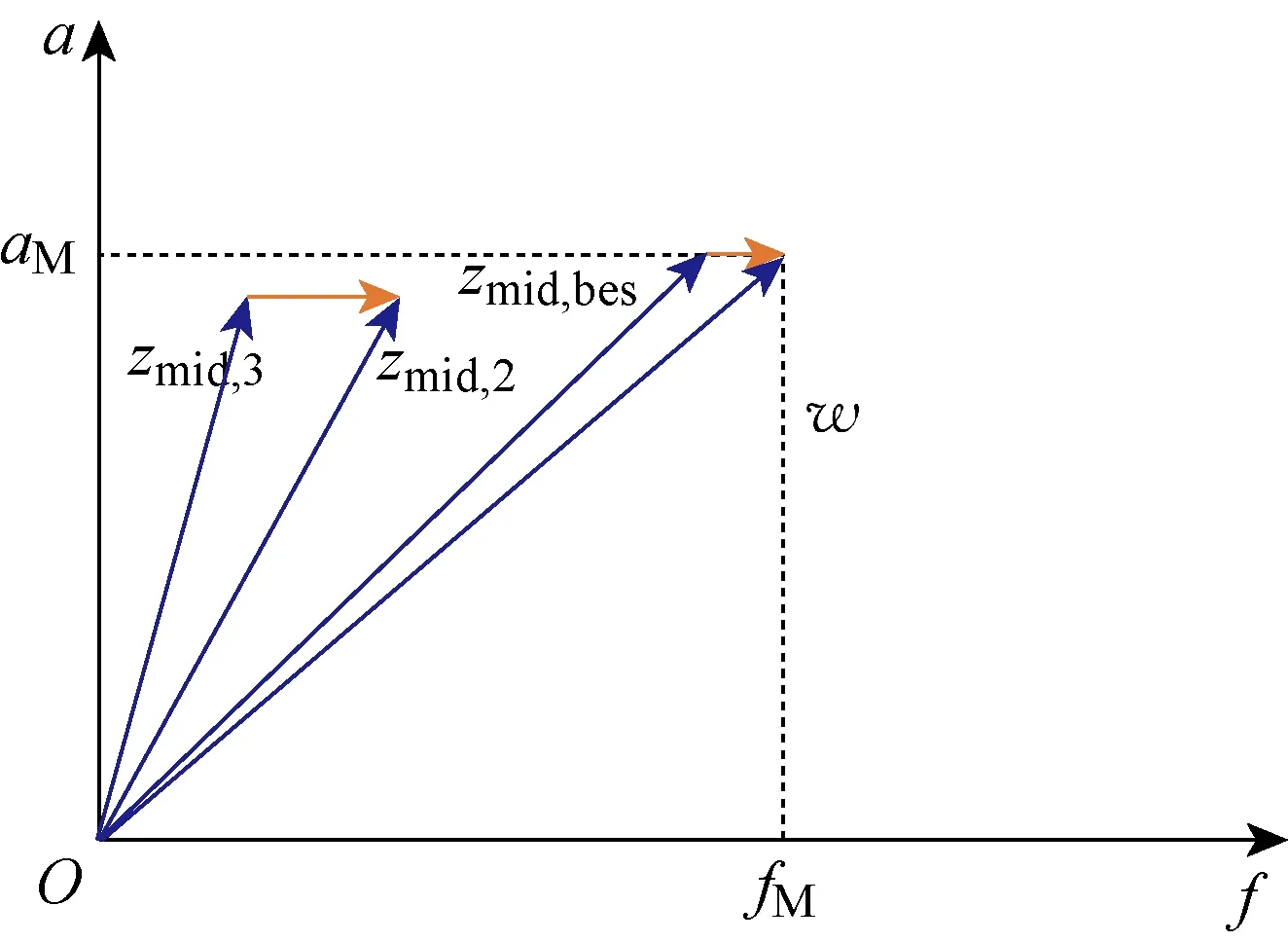
图7 后期变异操作模式Fig.7 Later mutation operation mode
(3) 交叉操作
交叉的对象为初始化的个体和变异生成的个体,通过交叉操作生成新的交叉个体.根据种群数量NP和交叉概率PC确定进行交叉的数量NC,NC=NP×PC.中层基因的交叉过程如图8所示.其中:aU、fU为初始个体的轨道半长轴和真近点角;aC、fC为交叉生成新个体的轨道半长轴和真近点角.
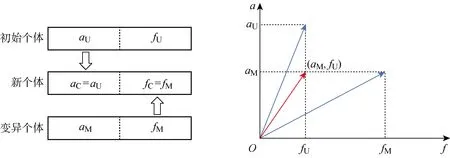
图8 编队卫星中层基因的交叉示意图Fig.8 Diagram of middle level gene crossing in formation satellite
3.3 基于Pareto支配的优劣评价标准
经过初始化、变异和交叉操作,种群获得了极大的丰富,对于个体基因,如何进行优劣评判进而对其取舍是算法中非常重要的一部分.由前文分析可知,位于下层基因中的分量是在编队规避中最为核心的指标,故在对不同个体进行优劣评价时,其评价依据主要是个体的下层基因.
对下层基因的优质性进行分析,选择4个个体z1~z4比较,如图9所示.由图9(a)可知,个体z1相对于个体z2而言,工作效率η较小、燃料消耗W较少且碰撞概率P也较低,因此无论从何种方面考虑,个体z1都更为适合.但由于经过差分进化后种群数量激增,基因多样性更加丰富,下层基因不同指标的优劣亦会出现区分,如图9(b)所示.个体z3相对于个体z4虽然燃料消耗W较少,但是其工作效率η和碰撞概率P却较大,在任务约束不明确的情况下,无法直接对其进行优质性比较.
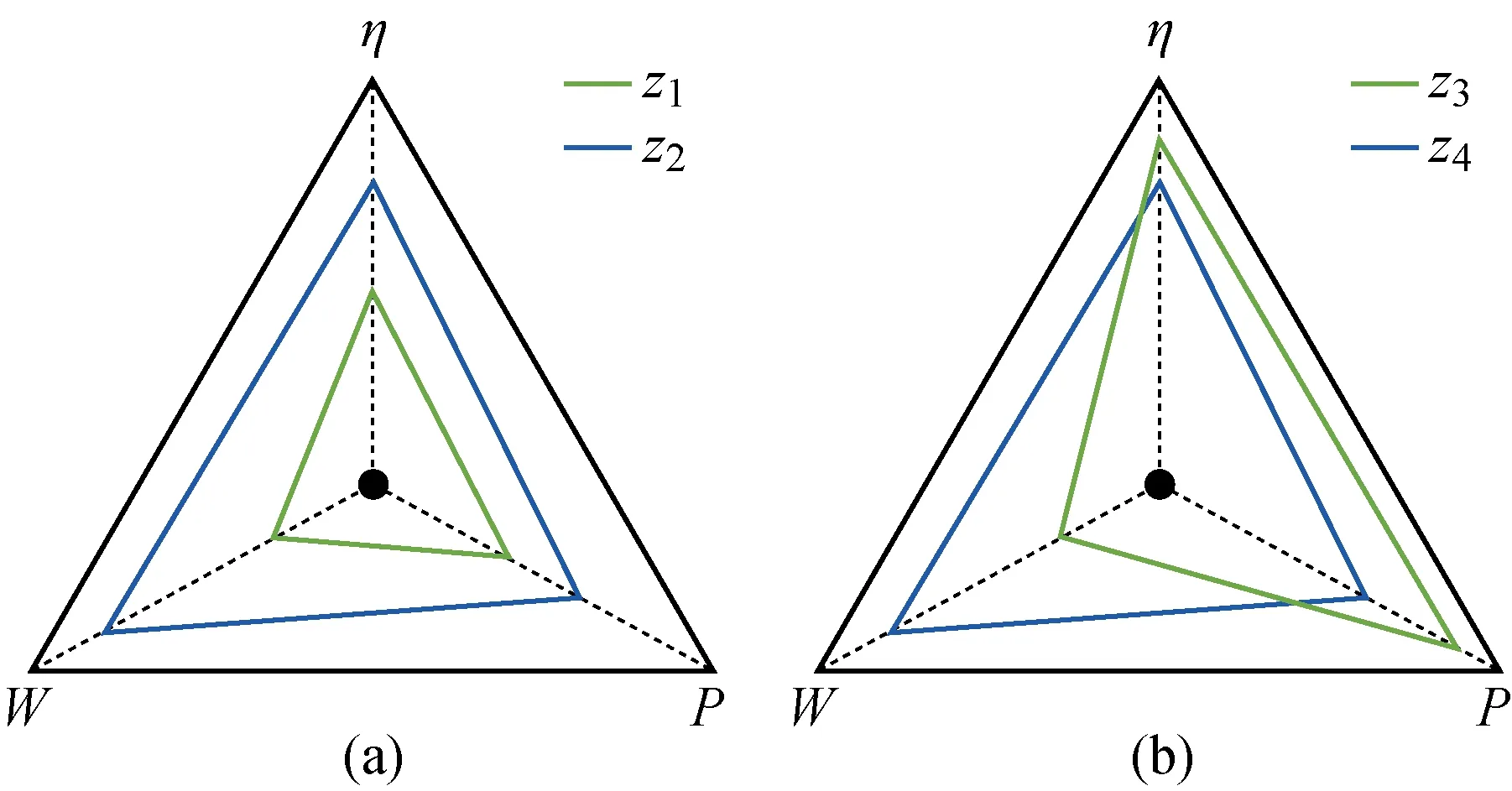
图9 个体之间的优质性比较Fig.9 Comparison of high quality among individuals
针对如何进行优劣评价问题,可采用Pareto支配思想,对种群中的每个个体进行快速非支配排序,以支配等级作为评价个体间优劣的标准,具体方法如下.
对于不同的两个个体zp和zq,其下层基因可表示为zp=(Pp,Wp,ηp),zq=(Pq,Wq,ηq).当以下两种情况同时发生时,可认为个体zp支配zq,即zp优于zq,记为zpzq:
(1) 个体zp中的所有分量都不差于zq对应的分量,即(Pp≤Pq)∩(Wp≤Wq)∩(ηp≤ηq);
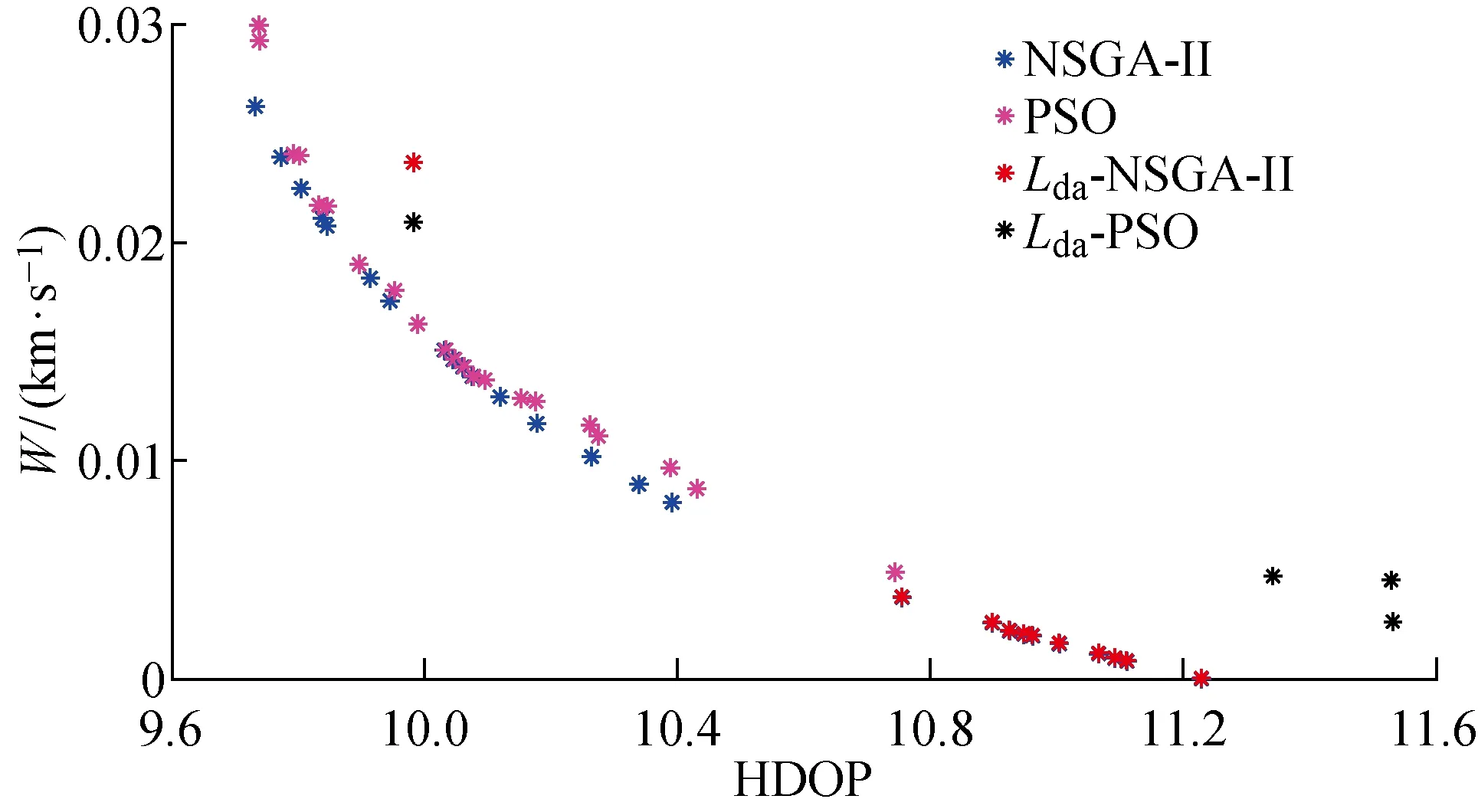
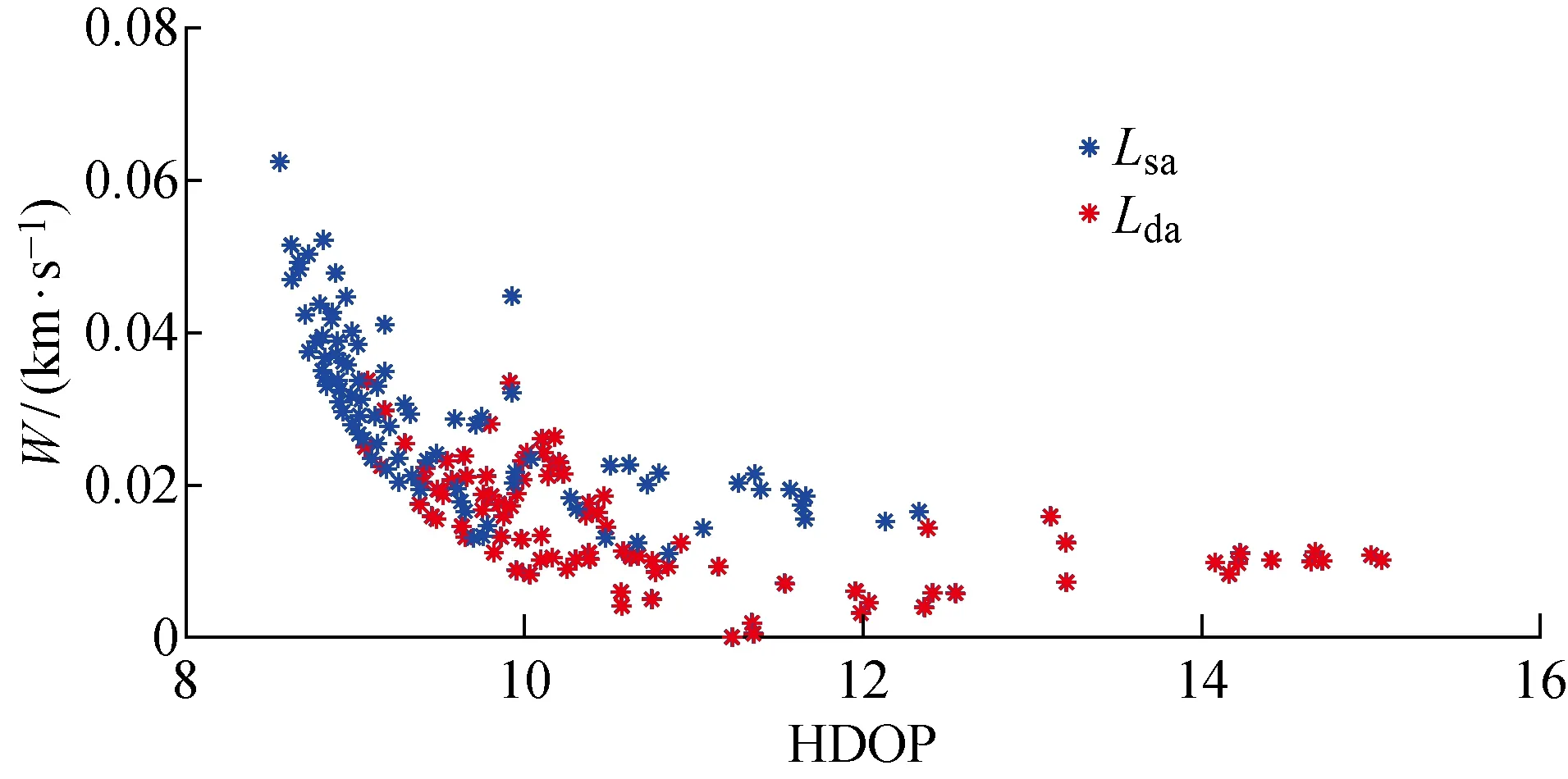
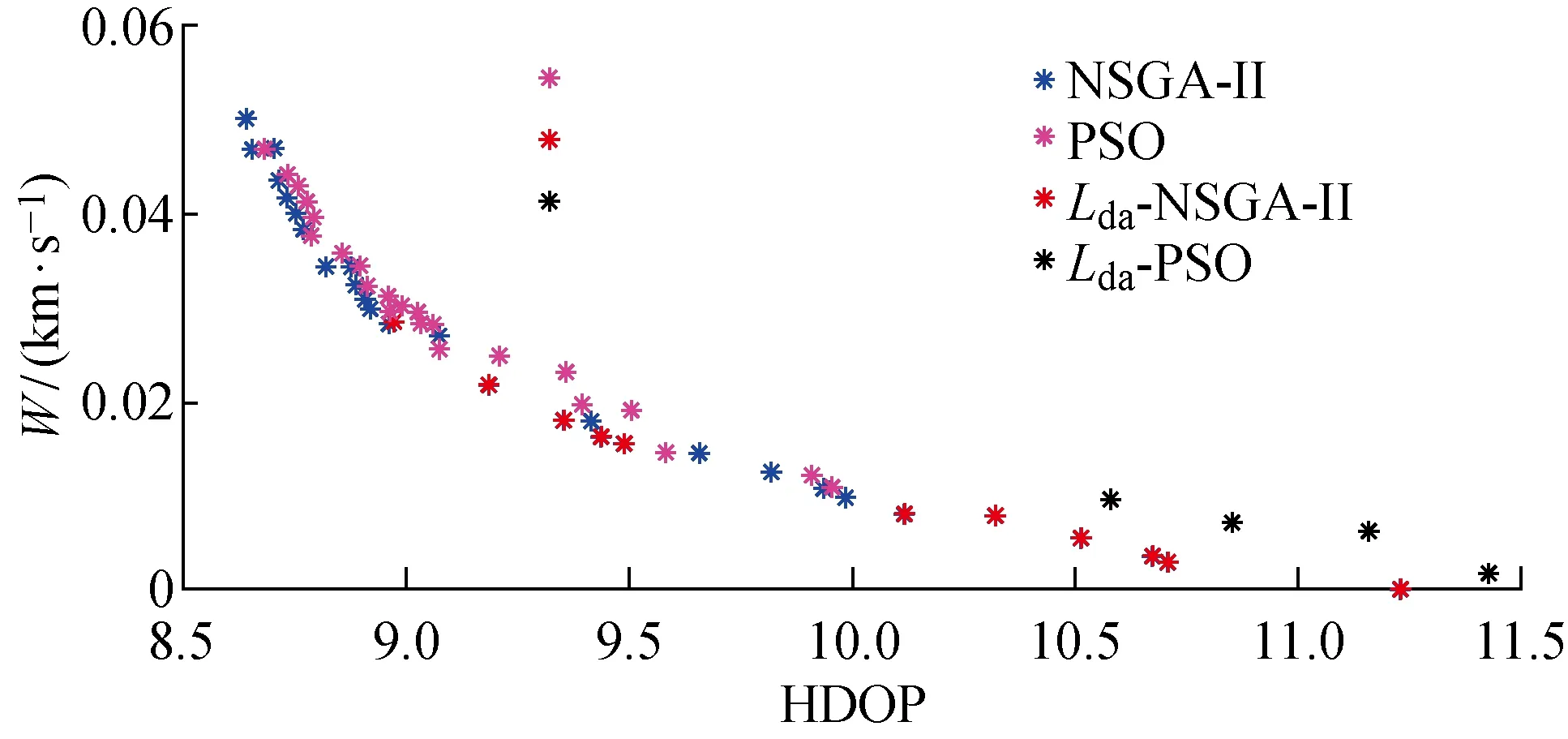
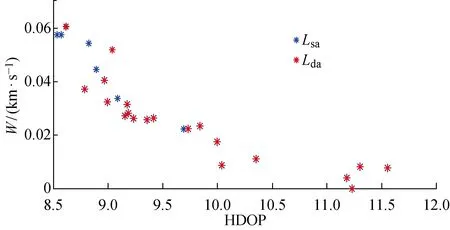
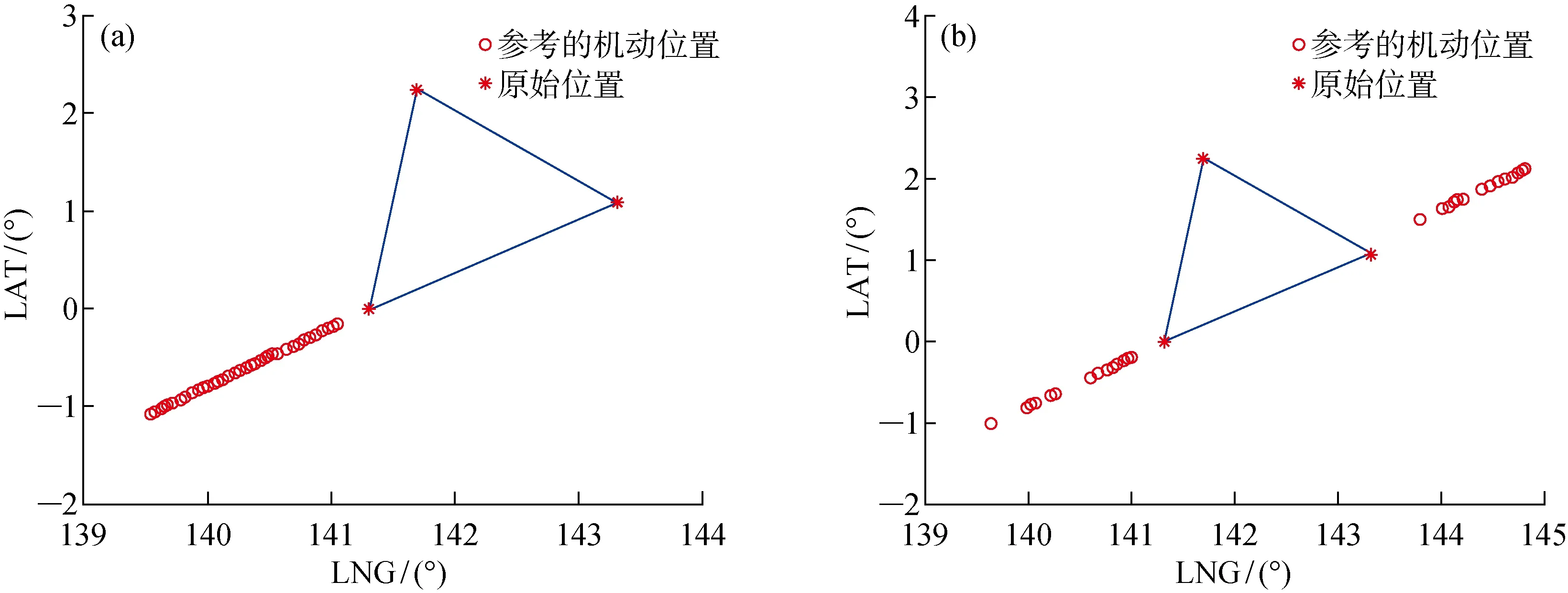
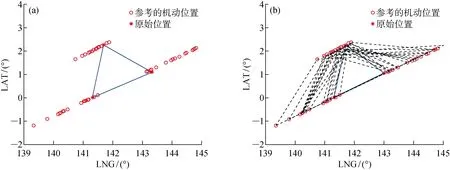
(2) 个体zp中存在至少一个分量,优于zq所对应的分量,即(Pp 根据Pareto支配的思想,个体z2优于个体z1,给予个体z2更加靠前的支配等级(见图9(a));个体z3和个体z4之间没有相互优于的关系,给予两者相同的支配等级(见图9(b)). 编队卫星碰撞规避中,碰撞概率是评价规避操作的最重要依据,若下层基因中出现碰撞概率高于预警门限(10-4)的情况,则可直接否定这一个体.故可将下层基因中的碰撞概率作为个体筛选的第1道门槛,且由基因中的机动消耗和工作效率对种群中的个体在二维坐标系中进行表述,如图10所示. 图10 编队卫星下层基因的二维示意图Fig.10 Diagram of lower level genes of formation satellites in two-dimensional view 根据Pareto快速支配排序方法,可以对每个个体进行支配等级排序,支配等级较高的个体更为优质,予以保留. 通过上述方法对种群中的个体进行优劣性评价,且由于经过变异、交叉等进化操作,种群数量势必会增长,为获取下一代个体,可采用精英保留策略,即优先保留支配等级较高的个体.当支配等级相同时,优先保留拥挤度较大的个体,以此将保留的个体作为新一代种群,重复进行进化和筛选,直到出现满足条件的最优解. 以3颗卫星构成的海洋侦察编队卫星为算例,在碰撞发生前1圈(约107 min)发出碰撞预警,随即对卫星进行轨道机动,对有碰撞风险的卫星进行相位机动.初始时刻卫星和危险碎片的轨道根数如表2所示.其中:e为轨道偏心率;i为轨道倾角;Ω为轨道升交点赤径;ω为轨道近地点幅角. 表2 编队卫星和危险碎片的轨道根数Tab.2 Orbital roots of formation satellites and dangerous debris 卫星在机动后产生一定的相位差,从而规避了危险碎片,同时也保证侦察编队卫星的定位性能处于良好状态,通过基于多目标优化算法比较卫星不同位置下的状态,确定合适的参数组合. 当编队卫星中的1颗、2颗和3颗卫星受到碰撞威胁时,利用不同优化方法的结果比较如图11~16所示.其中,红色与黑色点表示该位置仍然存在碰撞风险(P>10-4);Lsa为安全解;Lda为危险解;Lda-PSO为粒子群算法下的危险解;Lda-NSGA-II 为NSGA-II 算法下的危险解.进行比较的优化方法有:标准遗传算法、粒子群算法和NSGA-II 算法. 由图11~16可知,红色的预警点位置主要分布于坐标系的下方,这是由于当卫星燃料消耗较少时,与危险碎片之间的最小距离未能拉升到足够长,所以仍然存在碰撞风险.由图11和13可知,采用“遗传算法+比例筛选”后的卫星参考机动位置存在许多非优质解,主要集中在右侧,其在相同耗能情况下HDOP较高.相比较而言,利用粒子群算法和NSGA-II 优化算法筛选出的卫星机动位置,解集元素并不相互支配,可在设定任务目标的情况下迅速确定最优机动位置. 图11 单星规避遗传算法优化结果Fig.11 Genetic algorithm optimal results of single satellite avoidance 图12和14为多目标优化算法中粒子群算法与NSGA-II 算法的对比.由图12和14可以看出,粒子群算法所筛选出的基因个体处于NSGA-II 算法最优前沿之后,且分布较为离散,全局优化效果不理想.这是由于相对于改进的NSGA-II 算法,标准粒子群算法在寻优过程中缺乏对粒子速度的动态调节,易陷入局部最优,导致优化效果相对较差,而采用改进的NSGA-II 算法的优化结果更为理想. 图12 单星规避的PSO算法与NSGA-II 算法优化结果比较Fig.12 Comparison of optimal results of PSO and NSGA-II for single satellite avoidance 针对单颗卫星规避(见图12),卫星机动的能量消耗区间为[0.007 8,0.026 8] km/s,对应的HDOP范围为[9.73,10.38].在保证任务条件HDOP≤10的情况下,考虑机动消耗尽可能小,最佳基因对应的坐标点为(9.93,0.017 5 km/s),对应的真近点角为[358.800 3°,2°,4°]. 图13 双星规避遗传算法优化结果Fig.13 Genetic algorithm optimal results of double satellites avoidance 针对两颗卫星规避(见图14),能量消耗区间为[0.010 2,0.050 0] km/s,对应的HDOP范围为[8.64,9.97].在保证任务条件HDOP≤9的情况下考虑机动消耗尽可能小,最佳基因对应的坐标点为(8.90,0.029 8 km/s),对应的真近点角为[359.223 6°,3.408 1°,4°]. 图14 双星规避的粒子群算法与NSGA-II 算法优化结果比较Fig.14 Comparison of optimal results of PSO and NSGA-II for double satellites avoidance 针对全部三颗卫星规避(见图16),能量消耗区间为[0.022 5,0.057 7] km/s,对应的HDOP范围为[8.54,9.68].在保证任务条件HDOP≤9.5的情况下考虑机动消耗尽可能小,最佳基因对应的坐标点为(9.08,0.034 0 km/s),对应的真近点角为[359.106 3°,2.597 1°,3.134 7°]. 图15 三星规避的PSO算法优化结果Fig.15 PSO algorithm optimal results for triple satellites avoidance 图16 三星规避的NSGA-II 算法优化结果Fig.16 NSGA-II algorithm optimal results for triple satellites avoidance 将所得最优机动位置与编队卫星原始位置进行比较,三星编队海洋侦察卫星中的2颗和3颗卫星在进行真近点角调整后的位置分布如图17和18所示.其中:LNG为经度;LAT为纬度. 由图17(a)可知,当单颗卫星受碰撞风险进行机动时,需要尽可能将该卫星机动至使三星基线变长、星下三角形外侧处.由图17(b)可知,当2颗卫星受碰撞风险进行机动时,需要尽可能将两颗卫星分别机动至星下三角形外侧,将卫星基线拉长.由图18可知,当全部3颗卫星受碰撞风险进行机动时,同轨道2颗卫星的基线尽可能拉长,同时在保证无碰撞风险下,不同轨的单颗卫星机动至同轨卫星的中垂线附近,从而使其到两同轨卫星的距离差较小,保证三星结构的稳定. 图17 单颗/两颗卫星规避的最优质解集位置Fig.17 Best solution sets for single satellite/two satellites avoidance 图18 三颗卫星规避的最优质解集位置Fig.18 Best solution sets for three satellites avoidance 针对编队卫星在遭遇空间碎片威胁时的规避决策问题,通过基于多目标优化算法对编队卫星的规避模型进行优化分析,并以三星编队的海洋侦察卫星作为仿真算例进行研究.仿真结果表明: (1) 卫星可选择的规避轨道有许多,但并不是每条规避轨道都具有使用的价值; (2) NSGA-II算法可以对编队卫星规避轨道的选择进行优化,使得编队卫星在不受碰撞威胁的同时,燃料消耗和工作效率得到保证; (3) 针对三星编队海洋侦察卫星,可以根据不同的预警类型,分别对编队卫星中的一颗、两颗和全部三颗卫星进行规避轨道优化,为制定编队卫星规避策略提供了参考.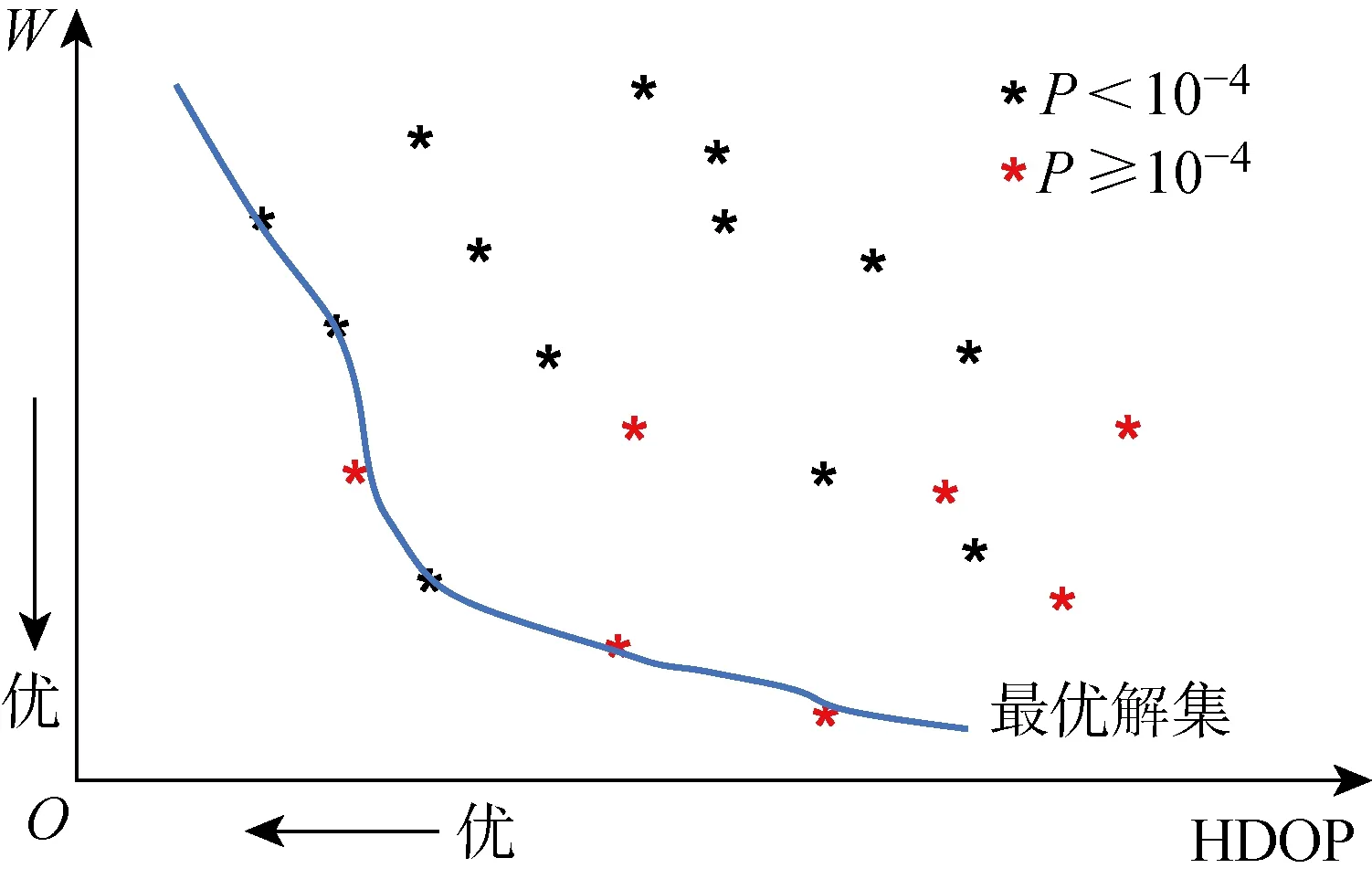
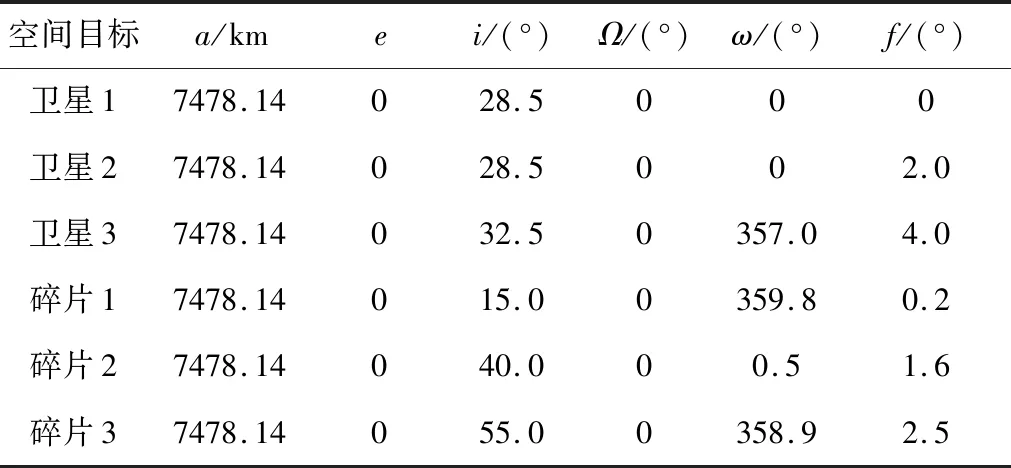
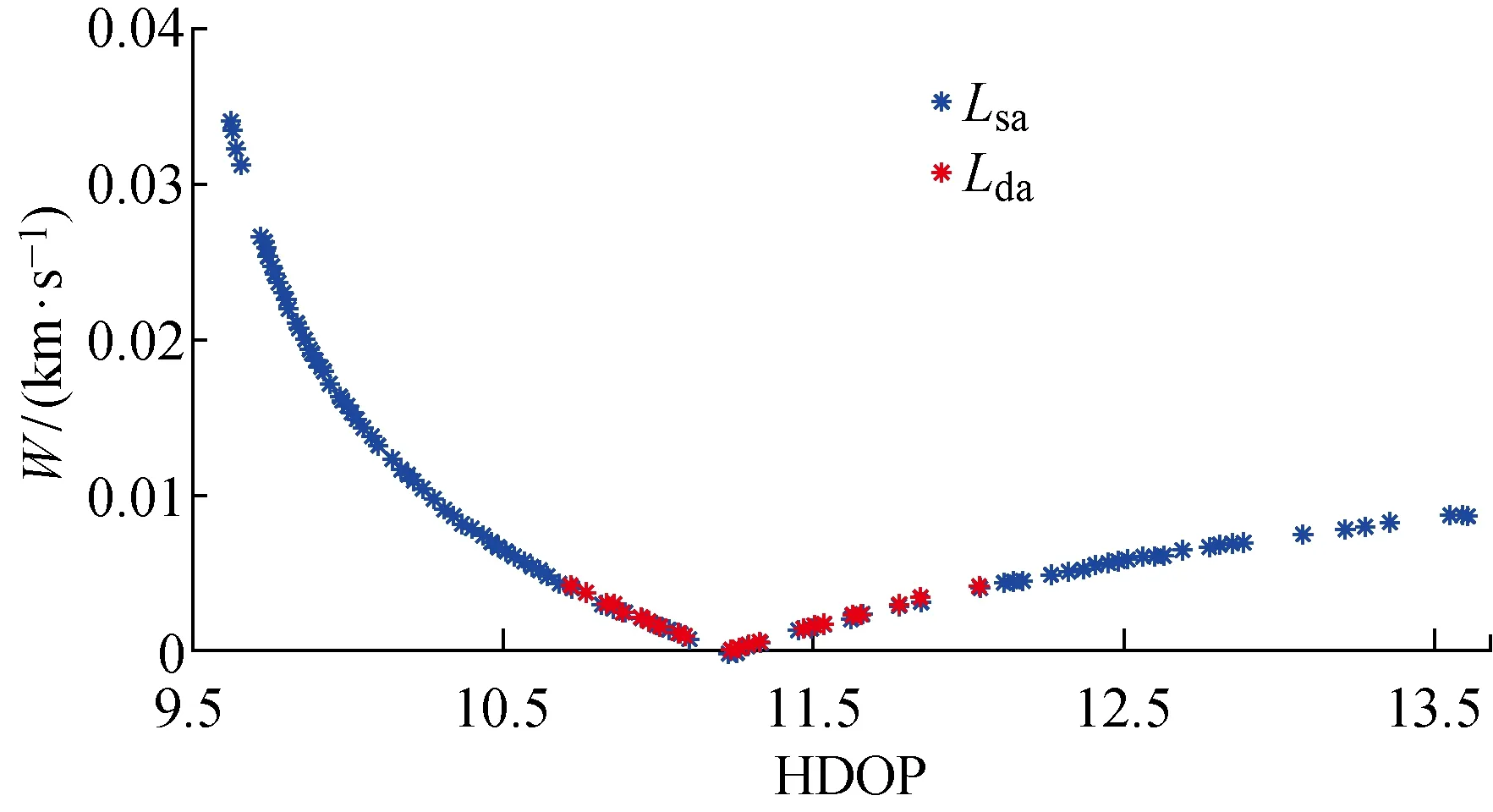
4 仿真算例

5 结论

